公路路堑挡雪墙防雪效果预测与设计参数优化
2022-10-14奚文彬李亚军常江芳刘亚男钱家珺李志达
奚文彬,李亚军,常江芳,刘亚男,钱家珺,李志达
(1.河北省高速公路延崇筹建处,河北张家口 075499;2.河北省金属矿山安全高效开采技术创新中心,河北石家庄 050043;3.石家庄铁道大学工程力学系,河北石家庄 050043)
风吹雪灾害是中国北方冬季常见的一种重大气象灾害,由于目前防雪技术不够完善,难以做到因地制宜、因害设防,致使雪阻路断现象频繁发生[1]。公路管理和养护部门要投入大量的人力物力进行除雪保畅,相比于灾后治理,灾前预防尤为重要。合理设置防雪措施,有效减少公路路面积雪,是降低或避免风吹雪灾害出现的关键[2]。
国内外学者对该领域进行了大量的研究,主要集中于风吹雪形成机理[3]、演化规律[4]以及雪害综合预防方法[5]。王中隆[6]综述了中国风吹雪的灾害特点,并针对性地提出了防治措施。总体上,高速公路的雪害预测和防治主要有2种途径,一是优化公路选线及路基断面形式[7],此方法用于高速公路设计阶段,通过优化公路走向和风的夹角,合理利用地势条件设计路堤、路堑或半路堤、半路堑等多种路基断面形式可大幅降低路面积雪[8];二是采用挡雪墙、防雪栅等防雪措施,此方法可用于高速公路运营阶段,通过阻挡、引流等将雪沉积在路面以外的区域[9]。
山区高速公路地形较为复杂,采用挡雪墙、防雪栅等防治措施必须依据实际地形进行合理布置,方能取得良好的效果[10-11]。通过野外观测、室内风洞试验等手段可实现风吹雪灾害评价和防雪措施的布设[12-14],然而,研究结果往往应用于某一路段的局部区域,不具有普适性,难以获得适合公路全路段的风吹雪害预测模型和针对性的防治方案。采用数值模拟手段,对公路全路段各种工况进行综合分析,获得风吹雪分布规律和预测模型,优化防雪设施设计方法,可实现对公路全路段的风吹雪害的预防和治理[15-16]。
因此,本文以路堑形式公路挡雪墙为例,通过计算流体动力学(CFD)数值模拟获得公路风吹雪流场分布规律,利用回归正交试验方法,得出路堑形式下挡雪墙防雪效果预测模型,并提出挡雪墙参数的优化设计方法,可为路堑风吹雪灾害防治提供理论参考。
1 风吹雪影响因素选取及正交试验设计
1.1 影响因素选取
积雪的体积分数可反映公路路面雪害情况,将其作为数值试验的因变量。风吹雪灾害影响因素有很多,依据前人关于风吹雪灾害机理的研究成果来确定影响因素[17-18],遴选出平均风速,路堑深度,路堑边坡比,挡雪墙高度和挡雪墙布置距离等5个评价指标,分别作为自变量,依次记为x1,x2,x3,x4和x5。具体取值如表1所示。

表1 风吹雪灾害影响因素取值
确定了各个因素的上下水平,计算其水平的平均值,即为各个因素的零水平,用Zj0表示,上水平与零水平之差除以星号臂γ为因素的变化间距,用Δj表示。如式(1)和式(2)所示。
(1)
Δj=(Z2j-Z0j)/γ。
(2)
1.2 因素编码设计
将各个因素不同水平的取值进行线性变换,即将每个因素在不同水平上进行编码设计,如式(3)所示:
(3)
最终得到各个因素的编码取值如表2所示。
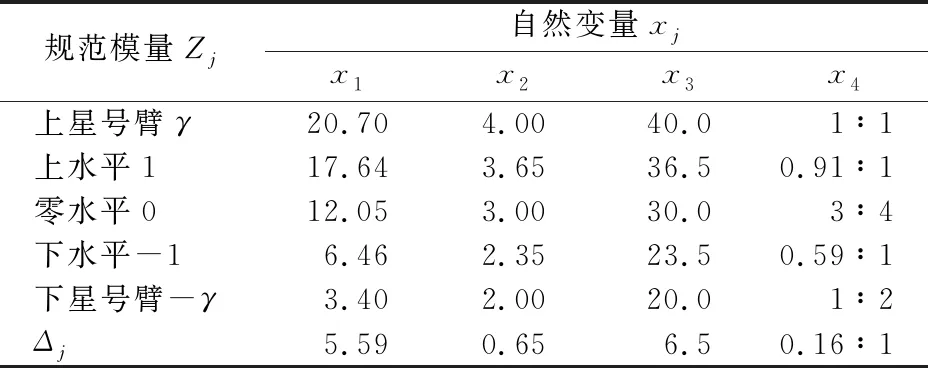
表2 各个因素编码设计
1.3 正交表设计与选取
正交试验通过运用较少的试验次数得出较好的试验结果,但是难以得出最优方案;回归分析是利用已有数据确定回归方程,但回归分析不涉及对试验设计的要求。因此,将二者结合起来,形成回归正交试验设计,既可给出合适的试验设计也可建立有效的数学模型,达到解决试验优化和预测的目的。
二次回归正交组合试验设计一般由3种类型的点组成。
1)二水平析因点:只选取+1或-1,这个试验点的个数为mc。根据全因素试验时,mc=2m;若根据正交表配置部分实施的试验点,1/2实施的试验点个数为mc=2m-1,1/4实施的试验点个数为mc=2m-2,改变mc的同时改变了误差自由度dfγ。
2)轴点:这些点与坐标轴原点距离为γ,且全在坐标轴上,取值为γ,-γ或0,通常称它们为星号点,个数为2m。
3)原点:各个自变量都取0的点,记为m0。本文取值为1。
试验处理数(N)为上面3种点的和,即:
N=mc+2m+m0。
(4)
本文选取了5个主要影响因素,通过式(4)计算得出应进行27次试验,最终确定选用的正交表。
2 公路路堑风吹雪数值试验
2.1 模拟参数设置与试验设计
公路路堑风吹雪模型见图1。模型入口边界采用速度入口(Velocity-inlet),出口边界条件为自由出流(Outflow),计算域顶部设置为Symmetry,计算域底部设置为Wall。本文采用风雪两相流模型数值模拟,取雪粒直径为0.000 2 m,雪相作为第二相稀相,雪粒体积分数为0.05,空气相为第一相。数值计算采用欧拉双流体模型(Eulerian),将颗粒作为一种特殊流体,考虑颗粒在空气中的扩散过程。
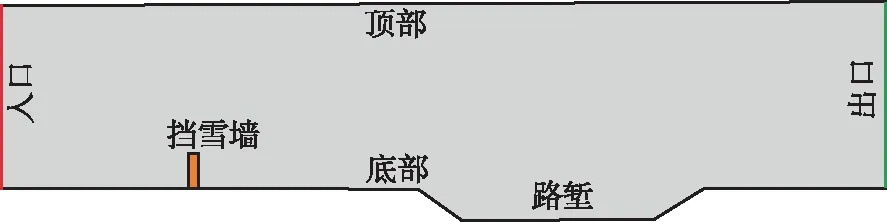
图1 公路路堑风吹雪模型
为了进行公路路堑风吹雪定量研究,本文将以初始风速、路堑边坡比、路堑深度、挡雪墙高度和挡雪墙布置距离为自变量,以积雪的体积分数为因变量,通过回归正交试验分析,得出防雪效果预测模型,从而准确地描述变量之间的关系。其二次回归方程模型如下:
(5)
2.2 模拟结果
采用CFD方法进行数值试验,结合正交回归试验设计,分析各因素对积雪的体积分数影响。本次研究首先需要进行27次数值试验,然后再将模拟结果指标进行回归分析,以达到本文研究目标。采用了5因素3水平的回归正交试验,由于试验次数较多,仅以试验9(图2 a))、试验13(图2 b))以及试验20(图2 c))典型数值模拟结果为例进行说明。
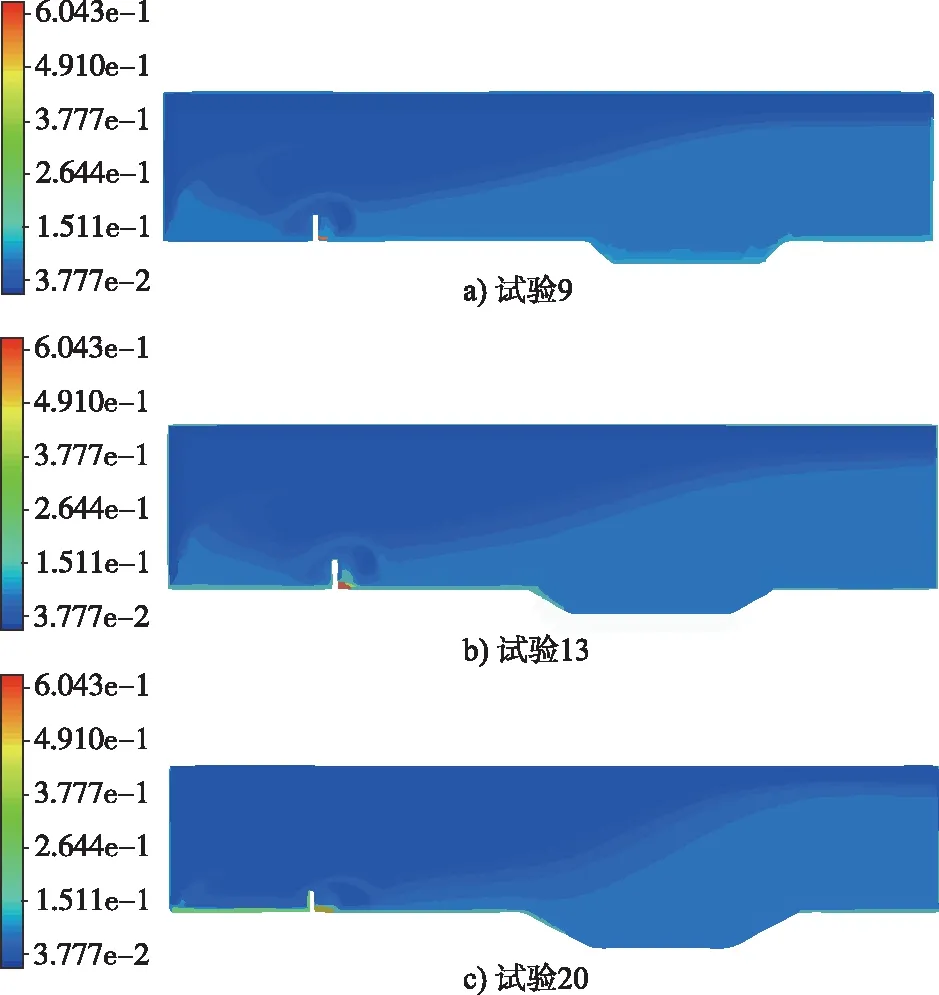
图2 积雪体积分数图
从图2中可以直观看出,风吹雪过程中产生的积雪主要集中在2个区域,即挡雪墙附近和路堑路面上,其中,挡雪墙后方积雪量最大,路堑周围积雪范围最大。通过CFD-POST导出数据,通过SPSS数据处理软件得出初始的回归方程为
y=134.342-1.955x1+6.008x2+5.281x3-
27.699x4+36.238x5-10.106x1x2-
9.204x1x3-1.004x1x4-4.589x1x5-
11.097x2x3+0.802x2x4-2.761x2x5-
0.338x3x4-1.820x3x5-3.512x4x5-
(6)
式中:x1为平均风速,m/s;x2为挡雪墙高度,m;x3为挡雪墙布置距离,m;x4为路堑边坡比;x5为路堑深度,m。
3 挡雪墙防雪效果预测模型
尽管已经得到初始防雪效果的预测模型,为了提高模型的准确性和可靠性,还需要进行显著性检验,将相关关系较小的项剔除,得到最终系数表(见表3)。最终的回归方程见式(7),模型相关性为0.975,相关性较高。
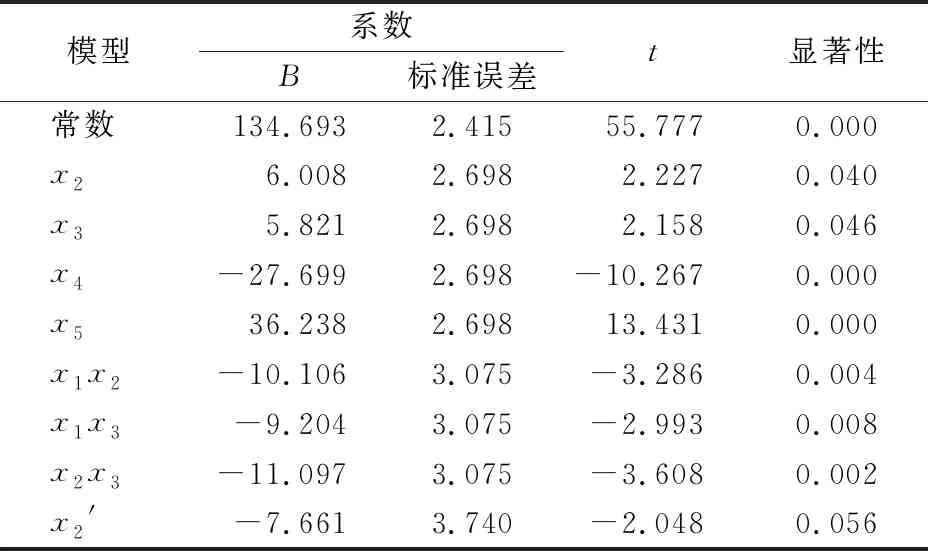
表3 最终回归方程系数表
y=134.693+6.008x2+5.821x3-27.699x4+
36.238x5-10.106x1x2-9.204x1x3-
(7)
将平方项进行正交变换公式可得:
(8)
将式(8)代入式(7)中可得:
27.669x4+36.238x5-10.106x1x2-
9.204x1x3-11.097x2x3。
(9)
由于前面进行编码设计,根据式(3)同时可以将方程回代,得到防雪效果的预测模型如下:
1.182Z3-172.931Z4+18.679Z5-2.781Z1Z2-
0.025Z1Z3-0.263Z2Z3,
(10)
式中:Z1为平均风速,m/s;Z2为挡雪墙高度,m;Z3为挡雪墙布置距离,m;Z4为路堑边坡比;Z5为路堑深度,m。
由最终防雪效果预测模型可知,公路风吹雪防治措施对路堑的影响因素包括平均风速、挡雪墙高度、挡雪墙布置距离、路堑边坡比以及路堑深度都对其产生影响,影响程度的大小可以通过回归方程式中各个变量系数的绝对值的大小判断。故影响程度从大到小依次为路堑边坡比>挡雪墙高度>路堑深度>风速>风速-挡雪墙高度组合>挡雪墙布置距离>挡雪墙高度-挡雪墙布置距离组合>风速-挡雪墙布置距离组合。
4 挡雪墙优化设计与防雪效果评价
4.1 挡雪墙优化设计
在实际工况中,风速、全路堑深度和边坡比可现场测量,而在挡雪墙设置过程中需要得到挡雪墙高度和布置位置。因此,可将风速、全路堑深度和边坡比作为已知量,将挡雪墙高度和布置位置作为未知量,获得预测积雪体积分数的二元三维曲面,采用求极值的方法对挡雪墙的布置进行优化。
通过野外调研,选取延崇高速易发生风吹雪灾害的金家庄螺旋隧道口为研究对象,测量得到路堑距离10 m处评价风速为10 m/s,路堑边坡比1∶1,路堑深度4 m。代入防雪效果预测模型中,可得到挡雪墙优化模型:
Z=83.489-18.132a2+113.137a+0.93b-0.263ab,
(11)
式中:a为挡雪墙高度,m;b为挡雪墙和路堑之间的距离,m。
鉴于挡雪墙的高度有限,选取挡雪墙高度范围为0~6 m,挡雪墙和路堑之间的距离一般为挡雪墙高度的10~15倍(长度为0~90 m)。
用于挡雪墙优化的二元三维曲面图见图3,通过求极值可得,当挡雪墙高度为6 m、挡雪墙和路堑之间的距离为90 m时,路堑路段积雪量最少,总的积雪体积分数仅为51.69,故此方案防雪效果较好。

图3 用于挡雪墙优化的二元三维曲面图
4.2 挡雪墙防雪效果评价
基于金家庄螺旋隧道口实测风速及路堑参数,开展无挡雪墙和有挡雪墙2种情况下的数值模拟,获得了积雪的体积分数分布,实现对挡雪墙防雪效果的评价。
图4和图5分别是无挡雪墙和有挡雪墙情况下积雪的体积分数分布图。显然,无挡雪墙情况下,整个路堑路段均有较大范围的积雪,且背风坡和迎风坡底部周围分布最多;有挡雪墙情况下,挡雪墙周围存在一定量积雪,而路堑路段上积雪明显减少,积雪仅仅少量分布在背风坡坡脚处,说明挡雪墙产生了阻雪效果,阻止了风裹挟着雪向公路路堑位置移动。

图4 无挡雪墙时积雪的体积分数分布

图5 有挡雪墙时积雪的体积分数分布
为了更加直观对比挡雪效果,绘制出路堑附近积雪的体积分数分布曲线,见图6。总体上,积雪体积分数随着路堑路段距离的增大呈现出先减小后增大至稳定、再减小的趋势。在路堑背风坡顶端,随着距离增加,积雪逐渐减少,但是到达路堑底端时,随着到达路堑路面雪的体积分数又不断增加,最后在背风坡中又开始下降。
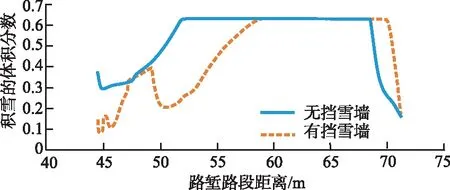
图6 路堑附近积雪的分布情况对比图
相比于无挡雪墙情况,有挡雪墙情况下路堑地段且靠近路堑背风坡位置的积雪量显著减少,总体上有挡雪墙时路堑附近积雪体积分数比无挡雪墙时减少了12.36%,表明挡雪墙的设置阻挡了路堑路段雪的堆积,起到了较好的防雪效果。因此,本文提出的挡雪墙防雪效果预测模型和挡雪墙布置优化模型可用于延崇高速路段风吹雪灾害评估,可为挡雪墙的合理布置提供科学方法。
5 结 语
针对路堑形式下公路风吹雪雪害问题,本文采用CFD数值模拟和正交试验方法分析了公路路堑风吹雪灾害挡雪墙防雪效果,建立了相应的预测模型,并对挡雪墙的设计进行了优化。主要结论如下。
1)影响风吹雪灾害积雪体积分数的因素包括平均风速、路堑深度、路堑边坡比、挡雪墙高度和挡雪墙布置距离。这些因素中路堑边坡比对挡雪墙防雪效果的影响程度最大,其次是挡雪墙高度、路堑深度、风速、风速-挡雪墙高度组合、挡雪墙布置距离和挡雪墙高度-挡雪墙布置距离组合,而风速-挡雪墙布置距离组合的影响程度最小。
2)通过风吹雪灾害挡雪墙布置优化模型,得出延崇高速金家庄螺旋隧道口路堑风吹雪挡雪墙最优高度为6 m、挡雪墙和路堑之间最优距离为90 m。同时,通过对比有无挡雪墙情况下路堑附近积雪分布情况的差异,发现在有挡雪墙情况下,挡雪墙改变了风吹雪灾害中积雪的分布范围,导致路堑路段积雪体积分数比无挡雪墙时减少了12.36%,证实了防雪墙的优化设置可起到较好的防雪效果。
本文研究可为风吹雪挡雪墙的设置方案提供依据,但由于影响风吹雪灾害因素众多,所提出的预测模型仍需在实践中进一步检验和完善。
