稀土电解槽槽电阻数据的降噪与分析

李科臻，王新春

内蒙古科技大学，内蒙古包头，014010

0 引言

稀土电解槽内部的槽况相当复杂，强热场、强磁场以及强电场之间会相互干扰，因而能够在线检测的信号少之又少，而槽电阻信号是为数不多的可以在线得到的反映槽体内部情况的信号。稀土氧化物的浓度会对槽电阻信号产生一定的影响，除此之外，槽电阻同时还会受到许多其他因素的影响。对于稀土槽电阻的解析，以往的文献十分稀少，而铝电解的电解工艺与稀土电解十分相似，本文从铝电解的槽电阻解析文献中发现，之前对槽电阻的解析都偏重于超低频信号，而把高频信号当作噪音滤掉，但是，越来越多的研究发现，槽电阻的高频部分也含有十分重要的槽况信息。所以，对槽电阻的分析应当尽可能细致，这对我们更好地了解稀土电解槽的运行状态有巨大帮助，对稀土电解槽内氧化稀土的浓度控制具有很大的价值[1]。

本文采集了某稀土厂6000A稀土电解槽典型的槽电压、系列电流数据，以稀土电解槽槽电阻为研究对象，对正常槽、碳渣槽以及添加稀土氧化物时的槽况进行了对比分析。采用小波除噪的方法对槽电阻信号进行除噪处理，然后运用快速傅里叶变换法和AR谱估计方法，对槽电阻信号的特征进行了深层提取，分析不同槽况下槽电阻信号的波动特征，为正确判断稀土电解槽的槽况，更好地控制氧化稀土的浓度提供了可靠依据。

1 稀土电解槽槽电阻信号构成介绍

由于稀土电解生产过程的自身特点，在已知的参数中，可以进行实时监测的信号只有系列电流和槽电压，以及由二者所计算出来的稀土电解槽的表观槽电阻。一直以来，槽电阻都是控制稀土电解过程中的重要参数。工业上计算槽电阻最普遍的计算公式为：

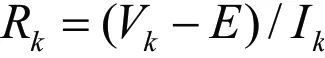
式中，Rk表示tk时刻的表观槽电阻，kV表示tk时刻电解槽的槽电压，E表示表观反电动势（一般设为常数），Ik表示为tk时刻的系列电流。

槽电阻信号大致分为两个部分，一部分是有用信号，即由稀土氧化物的浓度变化以及极距的变化而引起的槽电阻波动，这一部分的信号是稀土电解过程中正常生产控制而引起的低频信号，较为稳定，有一定的规律可循；另一部分则是干扰信号，大致可分为槽噪声和采样噪声，采样噪声是在槽电压和系列电流取样以及槽电阻计算时，引入一些与稀土电解生产过程特性无关的噪声，主要是由采样设备以及槽内复杂的磁场变化所引起的，而槽噪声是由于稀土电解过程中电解槽内部的原因而产生的槽电阻噪声，包括阳极故障、气泡排出、阳极有裂痕、脱落等引起的槽电阻大幅波动[2]。

需说明的是，稀土电解是一个恒流源的电解过程，系列电流十分稳定，所以系列电流的轻微波动并不会对槽电阻产生很大的影响。

2 数据来源及除噪方法

2.1 数据来源

本文所用数据均采自某稀土厂6000A稀土电解槽，采样频率是1Hz，频率的有效分析范围在0～0.5Hz，每组数据的采样时限为五分钟，每组采集的点数为300个。在采集数据样本时，避免了停炉所引起的信号变化，如换阳极、出稀土钕金属等，确保数据分析的准确性。

2.2 小波除噪方法

因为采集装置的固有缺陷，所收集到的槽电阻波形信息都会被或多或少的噪声污染。只要信号信息不经过除噪预处理，就必定会对频谱分析的准确性造成影响。因此本章重点就是探究怎样使用小波除噪的技术，对所收集到的槽电阻波形信息进行除噪预处理。

小波除噪的最基本方式如图1所示。首先，利用小波变换原理，将采集到的信息分散在不同的几个尺度当中，然后在每一种尺度下，先去除掉构成噪声的小波变换系数，最后再把构成信息的小波变换系数保存下来并将其增强，然后再通过反演小波变换，还原所要测量的信号。

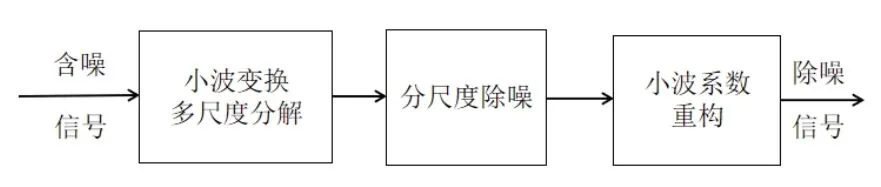
图1小波除噪原理框架

一般的除噪有三个步骤：①分解：首先选取一基小波和一层次N，然后计算在分层N时信号s的小波分解。②界限细节系数：针对任何一层次1～N，都必须有一个边界，并对细节系数采用阈值。③重构：使用N层的最原始的概貌系数来计算小波重构结果，并修正从一到N层的所有细节系数。

小波去噪性能一般采用信噪比、信噪比增益和均方根误差作为评价小波去噪效果的主要判断依据。根据一些通用的小波选择标准，并结合实际情况，本文将选择一些更合适的小波来对槽电阻信号进行除噪。随后利用大量实验对不同的信号进行去噪，算出相应的信噪比。信噪比的大小用来判断小波去噪特性的好坏。信噪比的定义如下：

求出不同槽况下采用不同小波基的信噪比，比较同一槽况下各小波基的大小，信噪比越大，则说明此小波对该信号的除噪效果最好。通过研究发现，在正常槽况下，dB20小波可以得到最大的信噪比；在阳极工作状况差时，需要用sym10进行滤波；在添加稀土氧化物时，采用dB12能够使信号表现出更好的效果；在碳渣槽时，dB12小波得到的信噪比最高[3]。

得到最佳小波基后，再对小波的分解层数进行确定，图2是dB20小波在不同分解层数时对正常槽槽电阻信号的信噪比，从图中可以看出，在分解层数为1的时候，除噪效果是最好的，当分解层数增大时，信噪比反而降低。后三种槽况与正常槽情况类似，所以，本实验的小波分解层数均选用一层小波分解。

回首《路线图》编制的过程，我们深刻感受到，这是国内印刷界首次历时最长、涉及领域最广、触及难点最直接、引起社会关注度最高的行业产业发展探索和实现印刷强国之梦的一场思想大碰撞、大讨论的过程；也是一个凝聚共识、开放交流、共同提升和全面受益的集智过程、一段饱受煎熬和顽强坚守的心路历程。

图2 dB20小波不同分解层数时信噪比

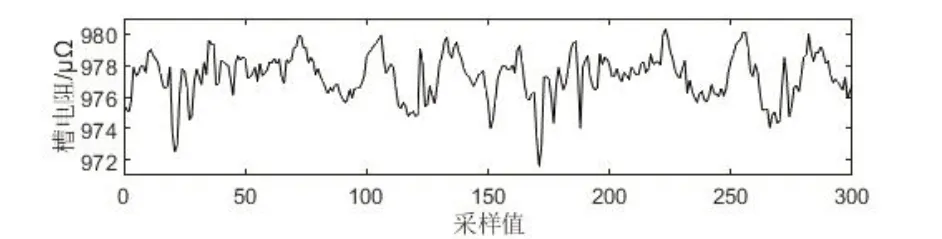
图3 正常槽原始信号

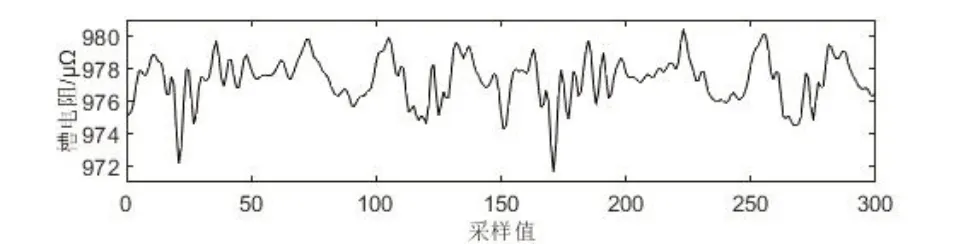
图4 正常槽分解层数为1时的除噪信号

图5 正常槽分解层数为2时的除噪信号

在选取了最佳小波基和分解层数之后，再对阈值函数和阈值规则进行选取。其中阈值函数分为硬阈值函数和软阈值函数，通过对原始信号和硬阈值、软阈值函数滤波后的信号进行对比，如图6-8，可以发现硬阈值函数滤波后的信号太过光滑，没有很好地保留尖角以及拐点等重要信息，而软阈值函数的这些信息则保留完好，并没有过度滤波。

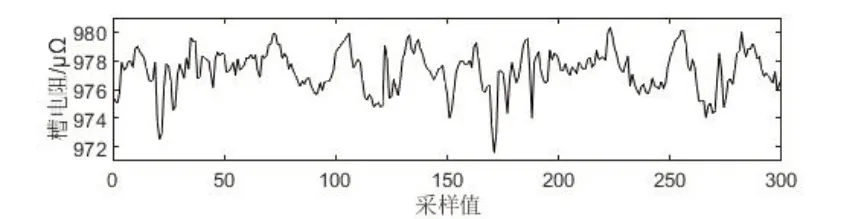
图6 正常槽槽电阻原始信号

图7 硬阈值除噪后信号

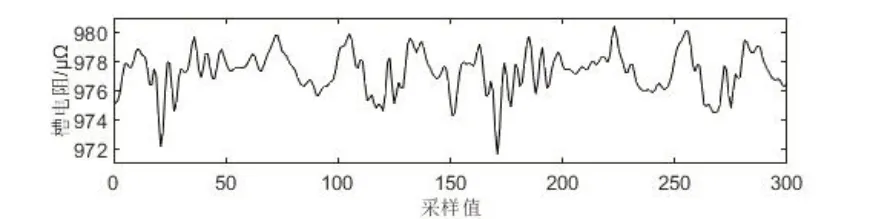
图8 软阈值除噪后信号

阈值选取的规则主要有以下四个：sqtwolog规则、 rigrsure规则、 minimaxi规则以及heursure规则。本文在选取了最优基小波和最佳分解层数以及选取软阈值函数的情况下，对四种规则在不同槽况下计算其信噪比，从而选取最佳的阈值规则。通过对不同阈值规则下的除噪信号进行信噪比比较，发现在四种槽况下，rigrsure规则的除噪效果均是最好的，所以，本文选取rigrsure规则为所研究信号的阈值规则。

2.3 实验结果

本文对稀土电解槽槽电阻在正常槽、在阳极工作状况差时、添加稀土氧化物时以及碳渣槽四种槽况进行了除噪研究，分析出了不同槽况下进行小波除噪所需的小波基、分解层数、阈值函数以及阈值规则，得到很好的除噪效果。除噪结果如图9-12所示。

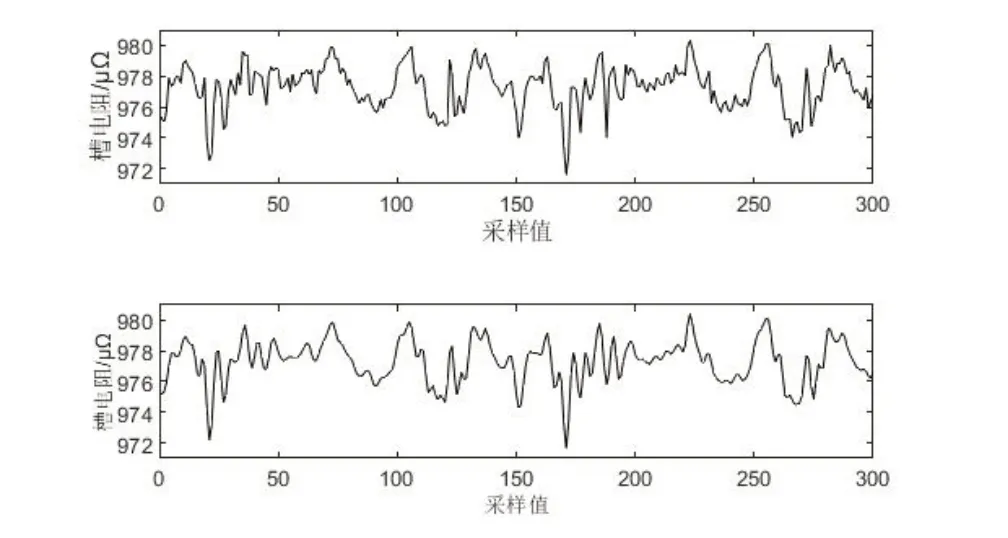
图9 正常槽除噪前后信号对比

图10 阳极工作状况差时槽电阻信号除噪前后对比图

图11 添加稀土氧化物时的槽电阻信号除噪前后对比图

图12 碳渣槽槽电阻信号除噪前后对比图

3 频谱分析

在本文中我们要对槽电阻信号进行数据分析，提炼出各个槽况的不同特征，归纳出槽况样本集。数据分析的方法有很多种，如聚类分析、回归分析、方差分析、时域分析、频谱分析等等，每种分析方法都有不同的适用条件。如聚类分析需要不同的数据类，本课题的数据类别较少，并不适用。

稀土电解槽在工作过程中，与工作状态相关的各项物理量随时间的改变而出现了相应的变化规律，这种信号中往往含有对设备状态鉴别和判断十分有益的信息。合理地分类、处理上述信息，构建它们和稀土电解运行状况间的联系，是对电解槽槽况识别的基础。但对信号的时域映射分析通常只是获取十分有限的信息，为了更方便高效地实现槽况识别，需要对信号进行频率区域分解，提取其特点。一旦发现某种性状和槽子的某种状态存在很大的影响关系，就会取得良好的分析效果。所以，本文对稀土电解中唯一可以在线得到的信号——稀土槽电阻信号进行了全面的频谱分析。

对信号进行频谱分析的意义是：（1）分析槽电阻的主频率区对槽电阻的产生的影响；（2）分析在不同槽况下，各槽况中高低频噪声的特征；（3）将这些特征用在神经网络的槽况识别中时，提取各自槽况的不同特点，为槽况识别提供有利依据。

3.1 基于离散傅里叶变化的频谱分析

傅立叶变换是谱分析的一个重要手法，一种波形的傅立叶变换的实质是将这种波形分解成许多频率上不同的正弦曲线之和。而当这种正弦曲线重叠起来并成为了原来信号波形的话，那么，也就成立了这种波形的傅立叶变换。傅立叶变换能够辨认出并区别开构成任意波形的几个不同频段的正弦曲线以及它们之间相应的振幅关系[4]。在数学上，这个关系也可以描述为：

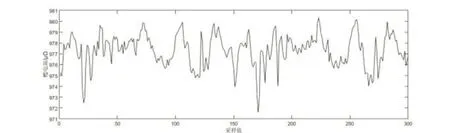
图13 正常槽时域波形

图14 正常槽槽电阻傅里叶变化频谱图

观察槽电压信号FFT频谱图，发现主频范围大致在0～0.1Hz左右，但因虚假谱峰过高，已无法辨别。为进一步提高谱的分辨率，进而分别选择了有较高分辨率的功率谱估计方法——直接法和AR谱估计方法进行实验。

3.2 经典功率谱估计方法

功率谱估计是频谱分析的主要手段，经典谱估计法属于非参数化方法。它也包括随机序列求谱的自相关法，和将序列直接用FFT求谱的直观法[5]。直接法都是直接经由傅立叶变换得出的；把随机信号的N点样本值视为能量有限信号，先取其傅立叶变换，得到后；而后再取其幅值的平方数，并除以N进行x(n)的真实功率谱的估算，即：

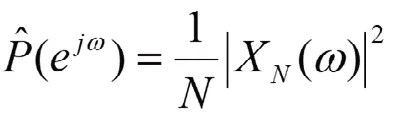
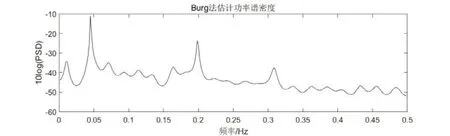
图15 正常槽经典功率谱估计

3.3 自相关法频谱估计

经典谱估计方法对序列的相关函数做了不合理的修改，不是对信号进行截断，就是将周期延拓，这都会给频谱估计造成相应的偏差。而现代频谱估计方法没有这些缺陷，它能够较好地解决这些问题[6]。AR谱估计具有分辨率高、平滑性较好等优点，AR谱估计的基本思想为：首先对随机信号序列形成AR模型，然后再使用模型系数计算信号的自功率谱。AR（p）模型的一般表述为：

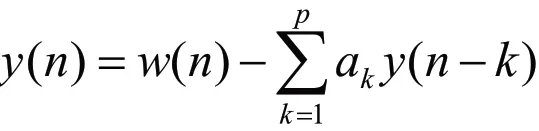
式中，y(n)为自回归随机序列；w(n)为一个零均值，方差2σ的正态分布有限带宽白噪声；p表示模型阶次。AR模型的输出功率频谱为：

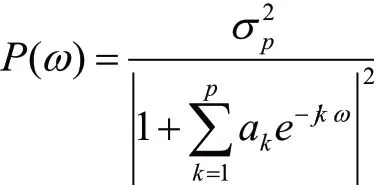
式中，p为AR模型的阶数，表示模型参量（或自回归系数），表示预测误差功率。

AR模型阶次p的选取对分析的效果有着明显的影响，p选取得太低，就反映不了谱峰；p选得太大，或许会形成错误峰值。在这里，使用最终预测误差的准则来帮助筛选模型阶次，该准则公式如下：

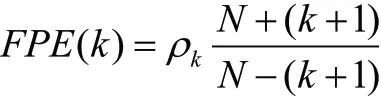
图16 槽况频域图

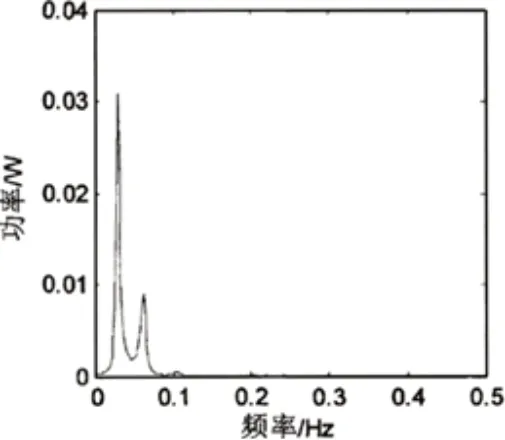
图17 阳极工作状况差时槽电阻频域图

图18 添加稀土氧化物时槽电阻频谱图

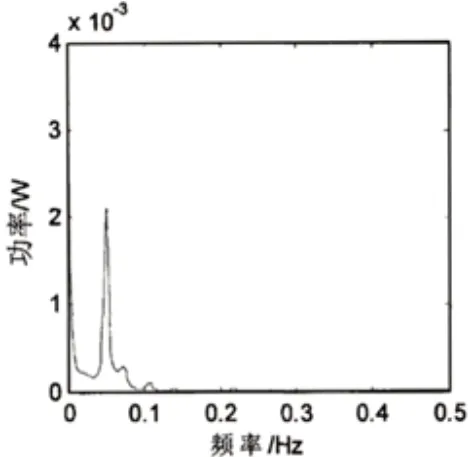
图19 碳渣槽槽电阻频域图

4 结论

本文先采用小波除噪技术对槽电阻信号进行了滤波处理，然后对四个槽况分别采用了频谱分析的方法，对三种谱分析方法进行了比较，发现自相关法频谱估计的效果较其他两种方法更好，并对不同槽况的频谱图进行了分析，具体分析如下：①在正常槽况下，观察槽电压信号的时域和频域，可以发现：槽电压波形振幅很小，此时虽然也存在磁流体运动，但是属于正常情况，不会对电解槽造成危害；在频率上，也只有一个非常明显的主峰，在0.03～0.04Hz之间，谱能量较低。②在阳极工作状况差时，除了有一个主峰外，在0.05～0.06Hz内还存在一个较小的次峰，主峰谱能量较正常槽有明显的升高。③在添加稀土氧化物时，除了有一个主峰外，0.04～0.05Hz处还有一个较低的次峰，主峰谱能量较正常槽高。