基于耐震时程法的连续刚构桥地震损伤分析

李 军，石 岩✉，张奋杰，王军文，黄兆国

1) 兰州理工大学土木工程学院，兰州 730050

2) 石家庄铁道大学道路与铁道工程安全保障省部共建教育部重点实验室，石家庄 050043

连续刚构桥跨越能力强、受力合理且整体性能良好，在跨越高山峡谷、深水河流时优势突出，因此在我国得到了广泛应用[1-3].近年来，我国加大了对西部地区的基础建设，高速铁路和公路线上的桥梁比重日益提高.但西部地区新构造活动强烈，断层与断裂带发育广泛，发生破坏性地震的概率非常大，故位于我国西部地区的桥梁结构具有较高的地震危险性[4-7].例如，2008 年汶川大地震中，接近完工的庙子坪大桥发生了主梁和主墩开裂、引桥落梁等严重震害，震后修复代价巨大[8].连续刚构桥一般采用悬臂施工法，施工工期较长，施工过程复杂且预应力损失和混凝土收缩徐变较大，使其施工阶段和成桥阶段的内力状态受结构自重、预应力、二期铺装荷载、施工荷载以及不同收缩徐变年限等因素的影响很大[9-12].因此，该类桥梁的结构体系与分析模型都不同于简支梁和连续梁等其它桥型.

目前，在对连续刚构桥进行抗震性能分析与评估时，一般采用常规分析方法，如非线性时程分析、静力弹塑性分析(Pushover)和增量动力分析(Incremental dynamic analysis，IDA)等.然而，针对同一个结构，采用这些不同分析方法时计算效率与准确性相差较大，且计算效率和准确性一般不可兼得.为此，一种集Pushover 方法和IDA 方法的优势于一体的新型抗震性能评估方法——耐震时程法(Endurance time method，ETM)应运而生，且近年来在国内外地震工程领域得到了较广泛的应用与发展[13-15].在桥梁耐震时程分析方面，郭安薪等[16]探讨了ETM 在少数几次计算与分析中预测公路桥梁碰撞反应的有效性和准确性，结果表明该方法具有足够的精度，可用于考虑碰撞效应的公路桥梁抗震分析和评估；He 等[17]将ETM 应用于考虑冲刷影响的公路桥梁地震易损性评估，认为与IDA 方法相比，基于ETM 的桥梁地震易损性分析具有更高的计算精度和效率；沈禹等[18]对考虑行波效应的大跨度矮塔斜拉桥进行了耐震时程分析，证明ETM 能够高效地预测出考虑行波效应的矮塔斜拉桥地震碰撞反应；郝朝伟等[19]针对高墩连续刚构桥进行耐震时程分析，通过与IDA 方法对比，验证了ETM 应用于此类桥梁抗震分析的高效性.从现有研究可知，使用ETM 的关键是合成地震动强度随时间逐渐增大的耐震时程加速度曲线(Endurance time accelerogram，ETA)，进而通过少数几次动力计算与分析即可得到结构在不同强度下从弹性、屈服、弹塑性直至倒塌阶段的抗震性能.然而，ETM 目前还未被用于考虑成桥内力状态的大跨高墩连续刚构桥抗震分析与性能评估中.

本文首先以一座大跨高墩连续刚构桥为研究对象，采用MIDAS/Civil 模拟其施工过程以获取成桥内力状态，再借助等效荷载法基于OpenSees 平台建立考虑成桥内力状态的动力分析模型；其次，依据《公路桥梁抗震设计细则》(JTG/T B02-01—2008)中的设计加速度反应谱合成了3 条耐震时程加速度曲线，通过对比ETM 与IDA 分析结果，验证了采用ETM 快速且准确地得到大跨高墩连续刚构桥地震反应的适用性；最后，基于该方法分析了主桥桥墩与引桥桥墩的墩顶位移、梁端位移及伸缩缝处的碰撞力等地震反应，采用位移延性系数μ和改进Park-Ang 双参数地震损伤模型的损伤指数DI[20]对桥墩损伤进行了量化分析与评估.

1 耐震时程法基本理论及地震动选取

1.1 耐震时程法与耐震时程加速度曲线

从合成耐震时程加速度曲线的过程可知，在从0 开始的某一时间段内，t时刻的目标加速度反应谱与该时间段内的持时t成线性关系：

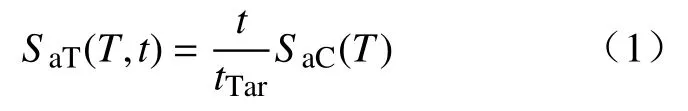
根据加速度反应谱与位移反应谱的函数关系，可得到t时刻的目标位移反应谱：

式中：tTar为目标时间；t为任意时刻；T为结构自振周期；SaC(T)为预先指定的目标反应谱(规范谱)；SaT(T,t)、SuT(T,t)分别表示自振周期为T的结构在t时刻的目标加速度反应谱和目标位移反应谱.

将式(1)和(2)转化为无约束变量的优化问题：

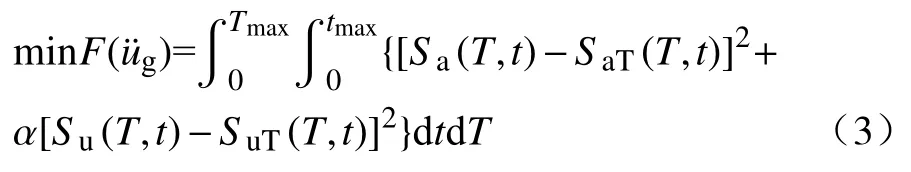
式中：üg为需要生成的耐震时程加速度曲线；α为位移谱的权重系数；Sa(T,t)和Su(T,t)分别表示t时刻的加速度反应谱和位移反应谱.

本文以我国《公路桥梁抗震设计细则》(JTG/T B02-01—2008)中的设计加速度反应谱为目标反应谱[21]，采用MATLAB 软件合成了3 条持时为30 s耐震时程加速度曲线作为输入，并取分析结果的平均值以使其精度更高.首先，基于白久林[22]编写的MATLAB 优化算法对式(3)进行求解；其次，利用SIMQKE 软件生成了与目标反应谱最为吻合的3 条人工合成地震动，其特征周期Tg为0.35，阻尼比为0.05，持时为30 s；然后，将3 条人工合成地震动作为初始输入地震动，采用MATLAB 计算得到持时为30 s 的3 条耐震时程加速度曲线(ETA1～ETA3)，如图1(a)所示.可以看出，地震动强度(加速度)随时间不断增大，符合耐震时程法的基本理念.同时，图1(b)给出了3 条耐震时程加速度曲线分别在0～10 s、0～20 s、0～30 s 的地震反应谱与目标反应谱，可以看出3 个不同时段反应谱的吻合度较高，进一步说明了优化算法程序的准确性.

图1 3 条ETA 曲线(a)及其加速度反应谱曲线(b)Fig.1 Three ETA curves (a) and corresponding acceleration response spectra (b)

1.2 地震动选取及等效耐震时间的换算

为验证ETM 评估大跨高墩连续刚构桥抗震性能的有效性和实用性，从PEER 数据库中选取了7 条天然地震动.地震动选取时依据PEER 调幅方法，以所选地震动的平均反应谱与目标反应谱能够较好地吻合为准.调幅后的7 条天然地震动在阻尼比为5%时的反应谱及其平均反应谱与目标反应谱的对比如图2 所示，可见7 条天然地震动的平均反应谱与目标反应谱能够较好地吻合.本文耐震时程地震动和天然地震动均沿纵桥向输入.

图2 7 条天然地震动反应谱及其与目标反应谱的对比Fig.2 Comparison for individual,mean and target response spectra of seven natural ground motions

不同地震动强度下结构的最大反应f(t)EDP可通过下式计算：

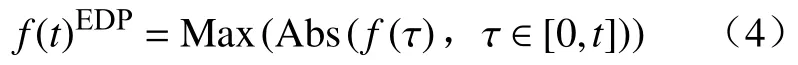
式中：f(τ)为结构在[0，t]时间段内的地震反应时程，对f(τ)取绝对值的最大值便能得到f(t)EDP.

为了将ETM 分析结果与IDA 分析结果进行对比，需要将做IDA 分析时的地震动强度转化为耐震时间t.本文以第一周期T1对应的加速度反应谱SaS(T)作为强度指标，单条天然地震动在取不同幅值时的等效耐震时间换算关系可表示为：

式中：tET为单条地震动取不同幅值时地震动强度的等效耐震时间；S1为单条地震动的调幅系数.

2 桥梁有限元模型

2.1 桥梁概况

本文以一座桥梁全长620 m、桥面总宽12 m 的大跨高墩连续刚构桥为工程背景，其中主桥是跨径为(120+220+120) m 的三跨连续T 型刚构，引桥是跨径为4 m×40 m 的四跨简支T 梁，如图3 所示.主桥上部结构为变截面单箱单室预应力钢筋混凝土箱梁；引桥上部结构为等截面钢筋混凝土T 梁，且每跨5 片；全桥桥墩均为钢筋混凝土桥墩，1#～2#墩为双薄壁空心墩，3#～6#墩为单薄壁空心墩.具体截面构造及尺寸详见图3.主桥采用悬臂施工法进行施工，施工时间约为460 d.上部结构采用C50 混凝土，下部结构采用C40 混凝土；主筋和箍筋分别采用HRB335 和HPB235 型号的钢筋，钢筋型号及直径详见图3；箱梁采用Strand1860 预应力钢绞线，共计452 束.0#桥台、3#墩墩顶各设置3 个盆式橡胶支座，7#桥台、3#～6#墩墩顶各设置5 个滑板支座.另外，桥台背墙处、相邻梁体间均设置伸缩缝(E1～E6).桥址场地类别为II 类，抗震设防烈度为9 度.

图3 大跨高墩连续刚构桥的构造形式与截面尺寸(单位：cm)Fig.3 Structural forms and section details of a long-span continuous rigid-frame bridge with high piers (unit: cm)

2.2 有限元分析模型

大跨高墩连续刚构桥的施工工期较长且其成桥内力状态受施工过程的影响很大.MIDAS/Civil 软件和OpenSees 地震模拟平台在桥梁施工过程模拟与非线性动力时程分析方面各具优势.本文结合两者优点，采用MIDAS/Civil 模拟实际施工过程，采用OpenSees 进行动力时程分析，将通过等效荷载法得到的等效内力荷载附加于OpenSees动力分析模型，使其处于真实内力状态.

(1) MIDAS/Civil 施工阶段分析模型.首先建立考虑施工过程中结构自重、预应力、二期铺装、施工荷载及10 a 收缩徐变等因素的有限元模型.按照悬臂施工法，整个施工过程共划分成38 个施工阶段，输入预应力钢束共计452 束，全桥附加二期铺装荷载，考虑10 a 收缩徐变.墩底固结，不考虑桩土相互作用.

(2) 基于等效荷载法的成桥内力状态.在MIDAS/Civil 中经施工阶段分析与静力分析后得到10 a 收缩徐变下真实的成桥内力状态，采用等效荷载法获取其内力等效荷载[23]，再将其附加到OpenSees动力分析模型，经静力分析后得到与成桥内力状态基本相同的等效内力状态，以便利用OpenSees进行基于成桥内力状态的动力分析.

(3) OpenSees 动力分析模型.基于OpenSees 所建立的全桥动力分析模型如图4 所示.关键受力部位(塑性铰区P1～P16)采用基于位移的非线性纤维梁柱单元模拟，且纤维截面上混凝土和主筋分别采用Concrete01 材料和Steel02 材料模拟.假设非关键受力部位处于弹性状态且都采用弹性梁柱单元模拟；采用双线性理想弹塑性弹簧单元模拟全桥支座，图4 中的Fy为屈服力，xy为屈服位移，k1为初始刚度，k2为屈服后刚度.采用接触单元法力学模型中的Hertz-damp 碰撞模型[24]考虑主桥和引桥梁体间、梁体与桥台背墙间的碰撞作用，图4中的ΔG为碰撞初始间隙，δy为屈服位移，δm为碰撞过程中最大侵入深度，Fm为最大碰撞力，K1为初始碰撞刚度，K2为屈服后刚度，Keff为有效刚度.模型阻尼比取5%，并采用瑞利阻尼.

图4 全桥动力分析模型Fig.4 Dynamic analysis model of the bridge

(4) 动力特性分析.为验证采用MIDAS/Civil 和OpenSees 分别建立的有限元模型的一致性和合理性，同时为保证动力计算结果的正确性，对两个模型分别进行动力特性分析.前5 阶自振周期和振型描述见表1，TM为MIDAS/Civil 计算周期，TO为OpenSees 计算周期.前5 阶自振周期的最大误差不超过5%，且此误差主要来源于软件差异，故所建OpenSees 模型与MIDAS/Civil 模型基本保持一致.

表1 前5 阶自振周期Table 1 First five-order natural vibration periods s

3 耐震时程法的适用性验证

基于OpenSees 平台，对所建动力分析模型分别输入耐震时程地震动和天然地震动.通过对比ETM 分析结果与IDA 分析结果，来验证ETM 在桥梁动力分析中的适用性.地震反应指标为墩顶位移、墩梁相对位移和伸缩缝处的碰撞力等.

(1) 桥墩位移.图5 给出了在ETM 和IDA 分析中主桥1#墩、引桥3#墩(过渡墩)的墩顶位移时程曲线.可见：将IDA 分析中不同幅值情况下的地震动强度转化为等效耐震时间后，桥梁地震反应随时间呈增大趋势，说明等效耐震时间的转化符合ETM 的主要理念；ETM 曲线为带平台段的锯齿状递增曲线，说明利用ETM 求出的桥梁累积最大地震反应在某一时间内不超过平台段地震持时所对应的地震反应；通过ETM 和IDA 分析得到的1#墩位移时程曲线在总持时内都较吻合，3#墩位移时程曲线在15 s 之前吻合度较高，超过15 s 后二者之间的离散性逐渐增大，但误差在可接受范围内.

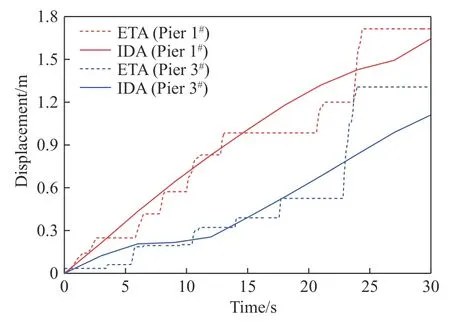
图5 桥墩墩顶位移时程曲线Fig.5 Displacement-time history of the top of the piers

(2) 墩梁相对位移.图6 给出了在ETM 和IDA分析中3#墩处主桥、引桥的墩梁相对位移时程曲线.可见：通过ETM 和IDA 分析得到的过渡墩处主桥的墩梁相对位移时程曲线吻合度较引桥要好，这主要是由于考虑碰撞效应时主桥与引桥的耦合作用对不同地震动的敏感性不同，且在15 s之前吻合度较好，15 s 以后吻合度降低，离散性增大，但整体来说，在前15 s 的耐震时间里便可以反映出结构的地震反应.

图6 3#墩处墩梁相对位移时程曲线Fig.6 Relative displacement-time history between pier and girder at pier 3#

(3) 碰撞力.图7 给出了在ETM 和IDA 分析中3#墩处、7#台处伸缩缝间的碰撞力时程曲线.可见对于3#墩，在持时小于10 s 时ETM 分析结果偏小，10 s 之后吻合度较高；对于7#台，在持时大于20 s 时ETM 分析结果偏小，20 s 之前吻合度较高.

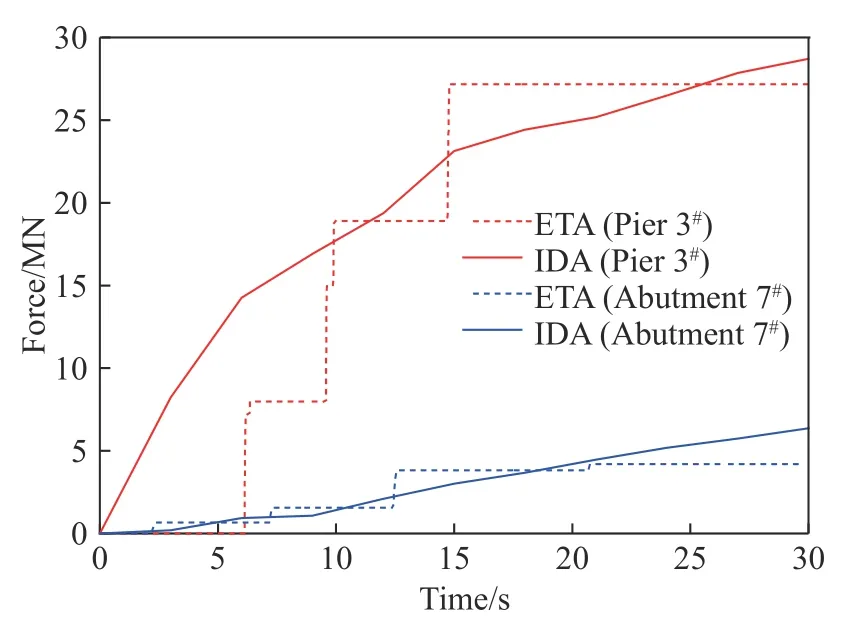
图7 伸缩缝间碰撞力时程曲线Fig.7 Pounding force-time history at the expansion joints

综上所述，针对不同地震反应指标，ETM 分析结果与IDA 分析结果趋势一致、相差较小.由此可见，耐震时程法在评估大跨高墩连续刚构桥的抗震性能方面不仅具有较高的时效性，其适用性也满足非线性动力分析的要求.

4 基于耐震时程法的地震反应分析与损伤评估

基于ETM 对大跨高墩连续刚构桥的地震反应和损伤状态进行量化分析.主要评价指标有：桥墩位移、梁端位移、伸缩缝处的碰撞力、位移延性系数以及Park-Ang 损伤指数.其中，由位移延性系数μd定义的桥墩损伤状态见文献[25]；由Park-Ang 损伤指数DI 划分的桥墩损伤状态见文献[26].

4.1 地震反应分析

图8 给出了ETM 分析中1#墩与3#墩的墩顶位移时程曲线；图9 给出了主桥梁端与引桥梁端的位移时程曲线；图10 给出了3#墩处与7#台处伸缩缝间的碰撞力时程曲线.可见：

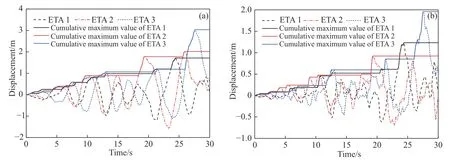
图8 桥墩位移时程曲线.(a) 1#墩；(b) 6#墩Fig.8 Displacement-time history of piers: (a) pier 1#;(b) pier 6#

图9 梁端位移时程曲线.(a)主桥；(b)引桥Fig.9 Displacement-time history of the top of the girders: (a) main bridge;(b) approach bridge

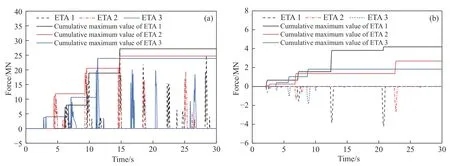
图10 伸缩缝处碰撞力时程曲线.(a) 3#墩；(b) 7#台Fig.10 Pounding force-time history of the expansion joints: (a) pier 3#;(b) abutment 7#

(1) 在较小地震动作用下，耐震时间较短，地震反应增长的平台段较短，近似线性增加，结构处于弹性阶段；而在较大地震动作用下，耐震时间较长，地震反应增长的平台段变长，相邻平台段之间的反应突变值增大，说明结构进入了非线性状态.

(2) 在相同的耐震时间下主桥和引桥的地震反应不同.例如，对于ETA2，在耐震时间为10 s 时，1#墩墩顶累积最大位移为0.88 m，6#墩墩顶累积最大位移为0.43 m，主桥梁端累计最大位移为0.88 m，引桥梁端累计最大位移为0.95 m.

(3) 通过ETM 可以预测在不同伸缩缝处第一次发生碰撞的时间和第一次发生碰撞时碰撞力的大小.例如，对于ETA2，3#墩处伸缩缝间第一次碰撞的时间为4.4 s，碰撞力为2.2×103kN.

4.2 桥墩损伤评估

图11、图12 分别给出了ETM 分析中1#墩和6#墩的位移延性系数变化曲线、Park-Ang 损伤指数变化曲线.可见：

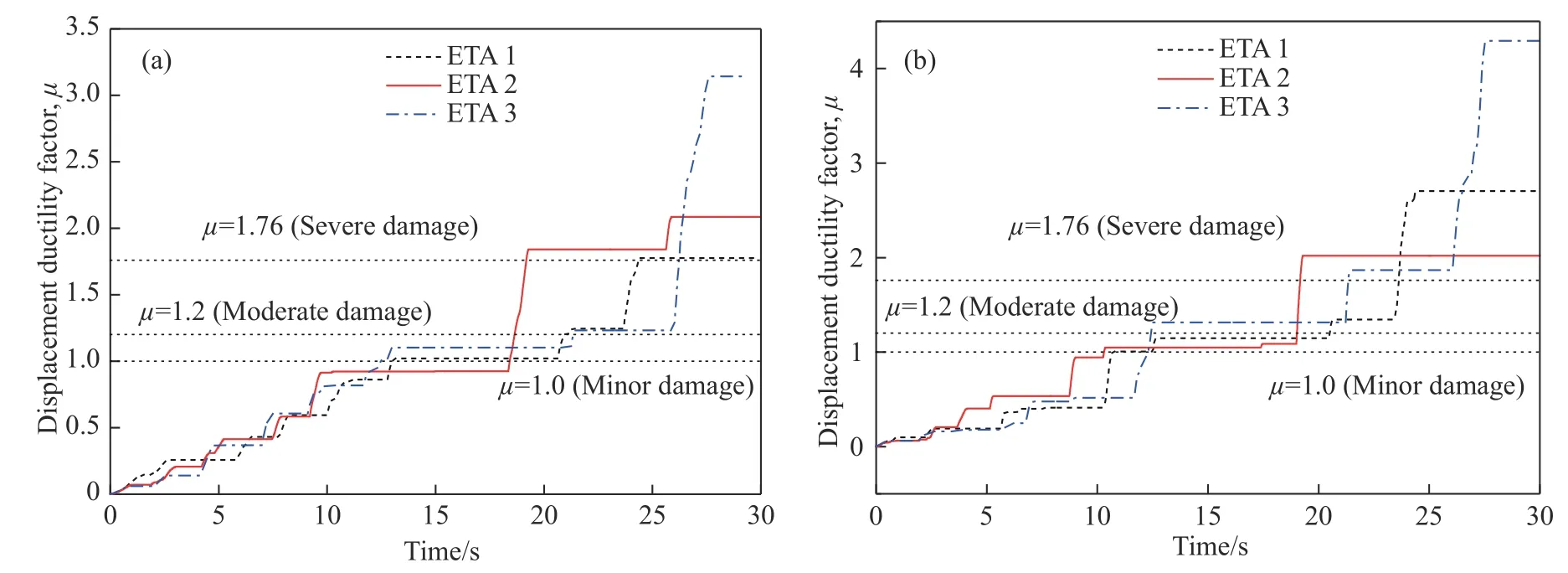
图11 桥墩位移延性系数.(a)1#墩；(b)6#墩Fig.11 Displacement ductility factors of piers: (a) pier 1#;(b) pier 6#

图12 桥墩Park-Ang 损伤指数.(a)1#墩；(b)6#墩Fig.12 Park-Ang damage index of piers: (a) pier 1#;(b) pier 6#

(1) 采用ETM 可以有效地预测大跨高墩连续刚构桥达到某一损伤程度的时间.例如，对于ETA2，1#墩达到中度损伤时，位移延性系数表征的耐震时间为18.64 s，Park-Ang 损伤指数表征的耐震时间为25.79 s.由于Park-Ang 损伤指数是基于变形和滞回能量的指标，故耐震时间较只单一考虑变形的位移延性系数指标要长，且更加准确.

(2) 在耐震时间较短时，1#墩的损伤小于6#墩的损伤；在耐震时间较长时，1#墩的损伤大于6#墩的损伤.例如，对于ETA3，在15 s 时1#墩的Park-Ang 损伤指数为0.039，6#墩的Park-Ang 损伤指数为0.056，在30 s 时1#墩的Park-Ang 损伤指数为0.817，6#墩的Park-Ang 损伤指数为0.595.

5 结论

(1) 大跨高墩连续刚构桥的ETM 分析结果较IDA 分析结果的离散性小；ETM 分析结果与IDA分析结果的平均值趋势一致，但存在一定的误差，此为耐震时程曲线与天然地震动在幅值和持时等指标上的差异所致，但作为一种简化方法，ETM 依然可以满足动力时程分析的适用性要求.

(2) 采用ETM 可以很好地预测不同地震动强度下的地震反应大小和达到某一损伤程度的时间；当以Park-Ang 损伤指数和位移延性系数为指标对桥墩进行损伤评估时，Park-Ang 损伤指数表征的耐震时间较位移延性系数更长，且更加准确，这是因为前者是基于变形和滞回能量的指标而后者只单一地考虑变形；在相同的耐震时间下，主桥与引桥的地震反应不同，且耐震时间较短时主桥桥墩的损伤小于引桥桥墩的损伤，耐震时间较长时则相反.

(3) ETM 仅需少数几次动力计算即可得到不同地震动强度下的地震反应，如墩顶位移、墩梁相对位移和伸缩缝处的碰撞力等，计算与分析效率高，这在大跨高墩连续刚构桥的非线性动力分析方面优势突出，可为这类大型复杂结构的抗震性能评估提供参考.