中心带孔等壁厚双层球缺罩EFP成型数值模拟
2022-10-14侯一方周春桂王志军尹建平孔繁家张肖江
侯一方,周春桂,王志军,尹建平,孔繁家,张肖江
(中北大学 机电工程学院, 太原 030051)
1 引言
现在战争中爆炸成型弹丸(EFP)应用广泛。但是单个EFP在面对一些新型防御设施时也显得力不从心。为了有效解决这一难题,多层串联EFP战斗部技术得到了广泛研究。
门建兵等采用数值仿真与试验相结合的方法,对双层EFP成型及侵彻问题进行了探究,试验采用脉冲X光拍摄到了EFP成型的过程,并研究了双层药型罩所形成的串联EFP对钢靶板的侵彻能力。郑宇等研究了药型罩不同材料对同轴EFP成型的影响,并对双层EFP的分离进行了探究。贺晶等开展了双层罩厚度匹配对成型特性影响的数值模拟,对其主要影响因素进行了对比分析。李惠明等开展了内外层材料匹配对双层EFP侵彻特性影响规律研究。龙源等采用数值模拟和实验相结合的方法,获得了曲率半径对双层药型罩EFP战斗部成型及侵彻特性的影响规律。伊建亚等对复合双药型罩结构所形成的射流对爆炸反应装甲侵彻及后效进行了研究,并且针对K装药,研究了不同材料药型罩对其装药性能影响,并对所提出的新型复合药型罩的射流成型情况进行了数值仿真。王哲等针对其典型装药结构,得出了双层药型罩所形成的EFP的速度计算模型。尹建平等指出:由中心开孔的等壁厚衬板形成的EFP不仅具有良好的径向收缩性能,而且具有良好的气动构型,金属损失较小。韩峰等对中心孔药型罩射流成型进行了数值模拟,得到了药型罩中心孔径、罩顶药高及中心护管材料等不同因素对中心孔药型罩射流成型的影响规律。贾子健等进行了中心带孔双层药型罩射流成型数值模拟,得出:在一定范围内双层药型罩开孔可提高射流速度,使得侵彻深度和孔径达到最佳。
目前,对于装药量不变,仅在药型罩上开孔的双层球缺药型罩的研究较少。本文在球缺罩压垮理论基础上,首先设计一种等壁厚双层球缺罩战斗部,其前后2层球缺罩中心带有圆孔,并运用Autodyn仿真软件,通过数值模拟的方式得出其开孔大小对EFP成型的影响;其次设计正交优化表,通过正交优化法得出一组较优参数;最后再与药型罩中心不带孔装药结构进行对比分析。
2 仿真模型
2.1 模型参数
本文所采用的战斗部结构示意图如图1,其中为装药高度,为装药直径且=100 mm,为壳体厚度,为两药型罩曲率半径,前后两药型罩均为等壁厚药型罩,第1层罩为远离炸药的钽药型罩,第2层罩为靠近炸药的铜药型罩且厚度均为,为第2层罩开孔直径,为第2罩开孔直径。
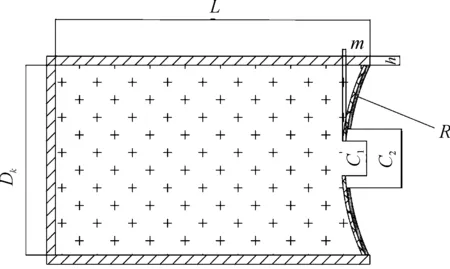
图1 战斗部结构示意图Fig.1 Structure diagram of warhead
仿真模型利用Autodyn仿真软件建立,对所有物质使用二维欧拉网格建模,并在空气边缘设置边界条件Flow_Out,此边界条件可以起到模拟无限空气域的作用,以点起爆方式引爆炸药,起爆点为底部中心点,(以>为例)建立有限元仿真模型,如图2所示。
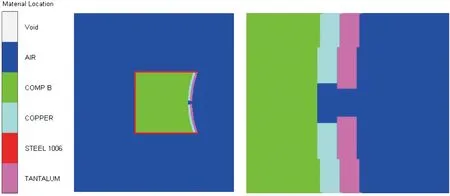
图2 有限元模型示意图Fig.2 Finite element model
2.2 材料模型参数
有限元仿真模型由聚能装药、壳体、空气域和双层药型罩组成,其材料选取均基于Autodyn自带的材料库。选取Steel_1006作为战斗部壳体材料,采用Shock状态方程和Johnson_Cook强度模型来描述战斗部壳体的变形情况。炸药选用B炸药,选用JWL状态方程来描述其复杂的爆轰过程,其状态方程参数见表1。前后两层药型罩均采用Shock状态方程,壳体及药型罩材料具体模型参数见表2。
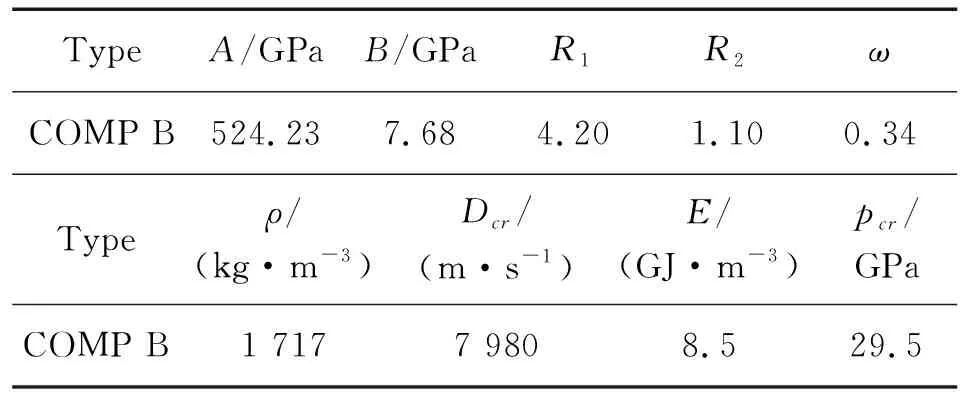
表1 B炸药JWL方程主要参数Table 1 Main parameters of JWL equation for B explosive
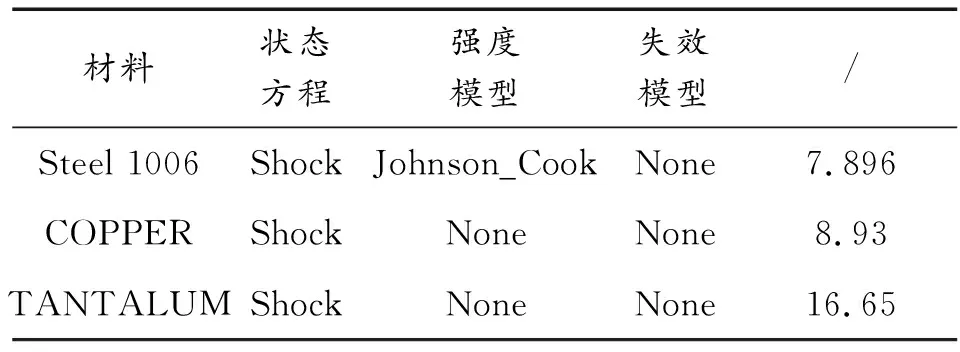
表2 材料模型参数Table 2 Material model parameters
3 药型罩不同开孔尺寸数值模拟结果分析
分别建立=、<、>等3种装药结构数值仿真模型,具体结构参数如表3所示。
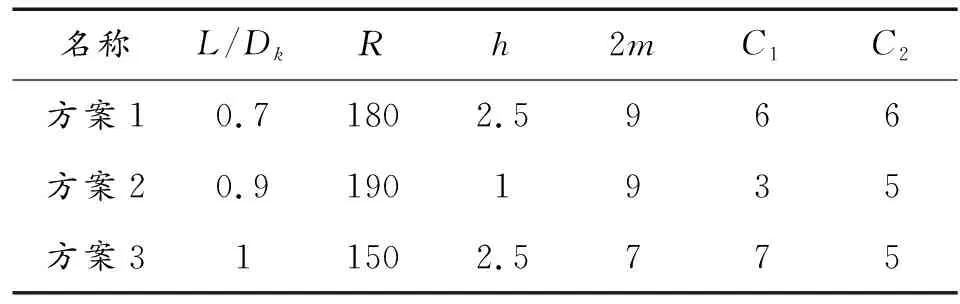
表3 不同开孔尺寸装药结构参数Table 3 Structural parameters of charge with different hole sizes
3.1 前后罩开孔尺寸相同时
在聚能装药起爆后,大约6 μs后爆轰波开始作用于铜罩,铜罩在爆轰波压力下先发生变形,在32 μs时前后药型罩所受爆轰波压力基本平均,并逐渐开始向后翻转,由于药型罩中心开孔,开孔处泄出速度会与药型罩变形速度形成速度差,此时铜罩与钽罩会有少量的崩出,此后药型罩进入拉伸阶段,在260 μs时铜罩在爆轰波径向压力作用下中心孔闭合,但钽罩在成型后未能发生闭合。方案1为不同时间药型罩上压力分布情况,如图3所示,方案1为不同时间所形成的EFP,如图4所示。
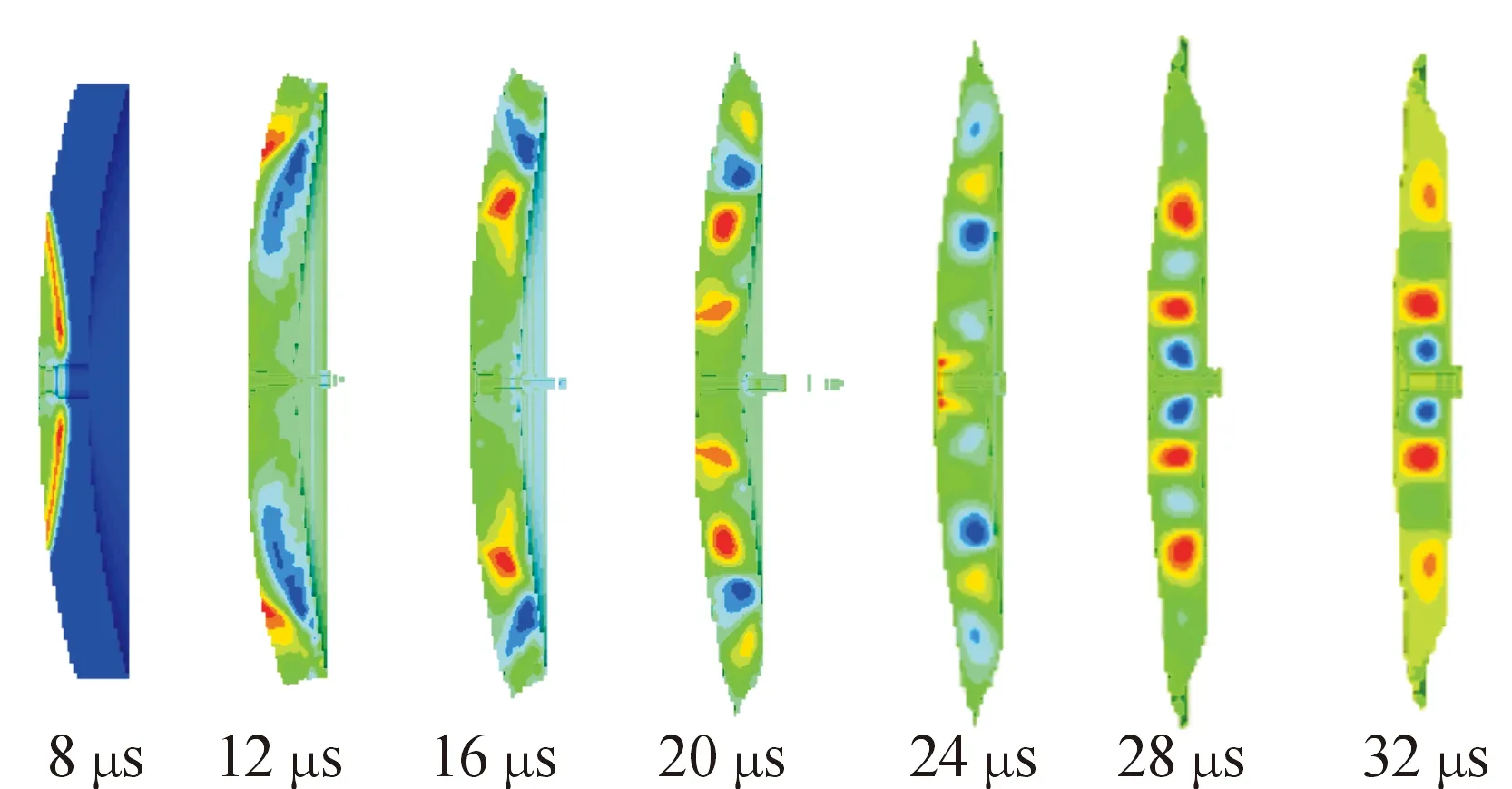
图3 方案1不同时间药型罩上压力分布情况示意图Fig.3 Scheme 1 pressure distribution on liner at different times
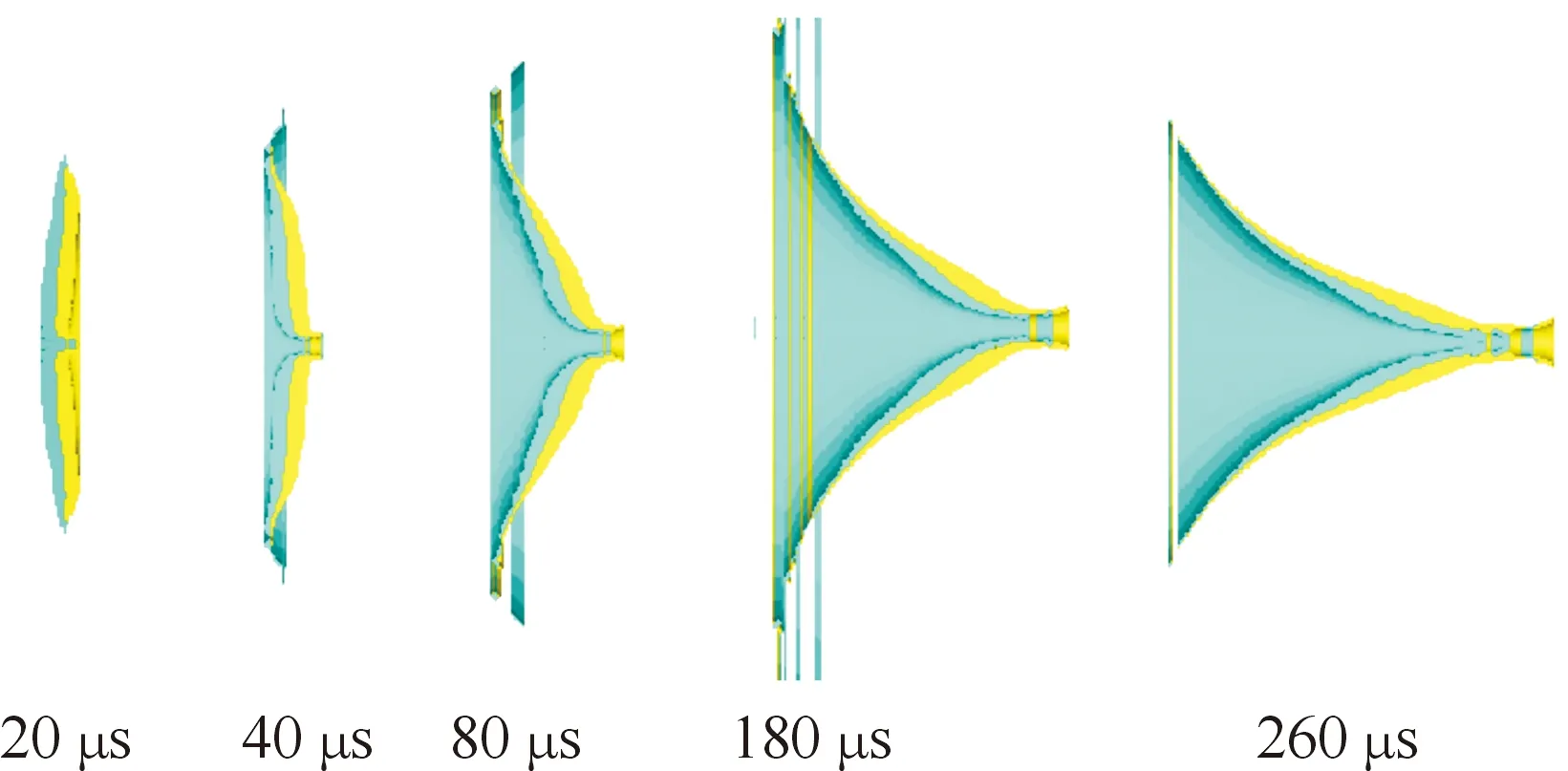
图4 方案1不同时间所形成的EFP示意图Fig.4 Scheme 1 EFP formed at different times
3.2 前后罩开孔尺寸C1在聚能装药起爆后,大约8 μs后爆轰波开始作用于铜罩,铜罩在爆轰波作用下先发生变形,大约30 μs时前后药型罩所受爆轰波压力基本平均,并向后发生翻转,由于<,开孔处铜泄出量相比=时较大,在进入拉伸阶段时,铜罩与钽罩均能闭合,但EFP弹体中后部径向收缩性较差。方案2为不同时间药型罩上压力分布情况,如图5所示,方案2为不同时间所形成的EFP,如图6所示。
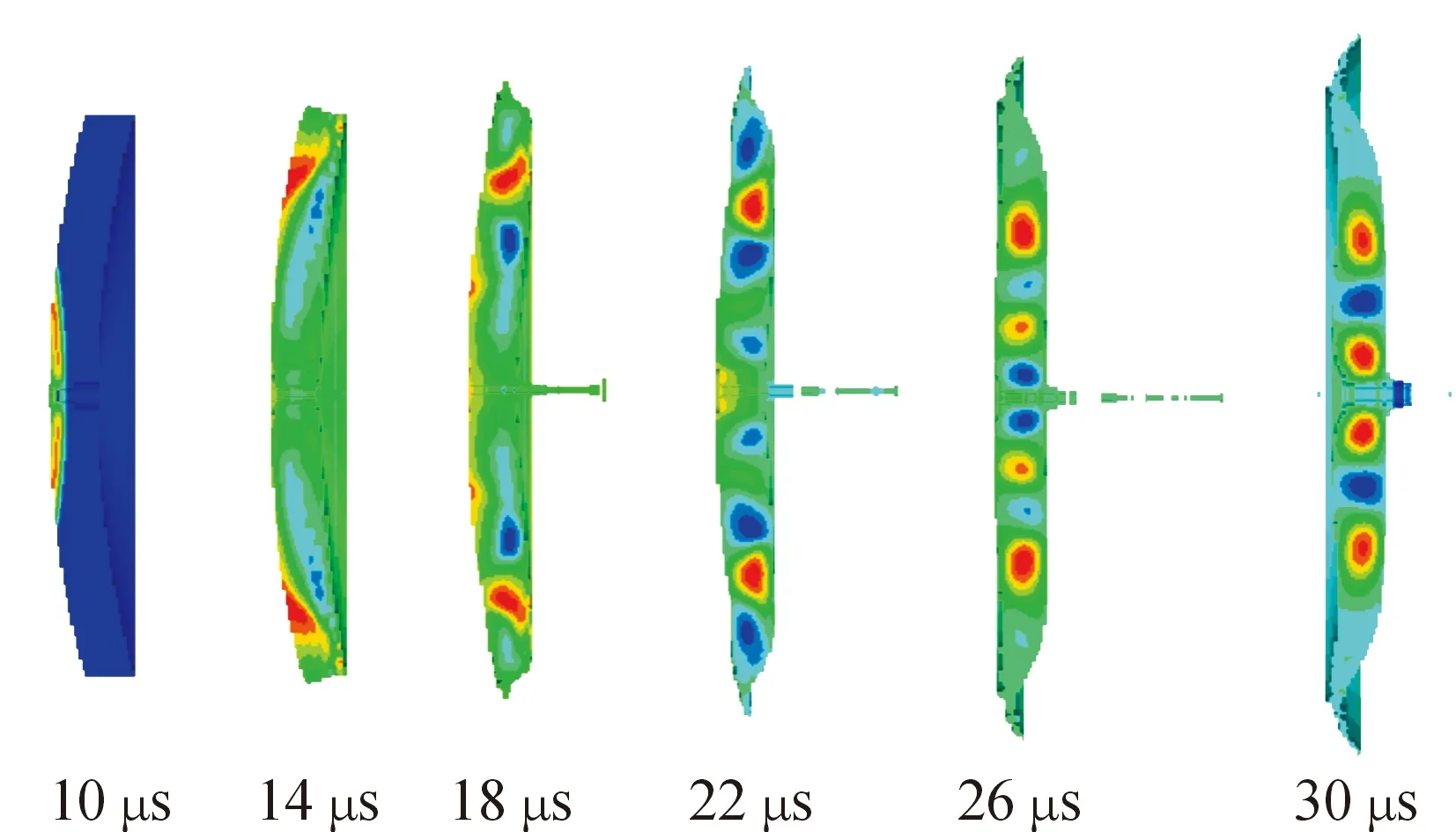
图5 方案2不同时间药型罩上压力分布情况示意图Fig.5 Scheme 2 pressure distribution on liner at different times
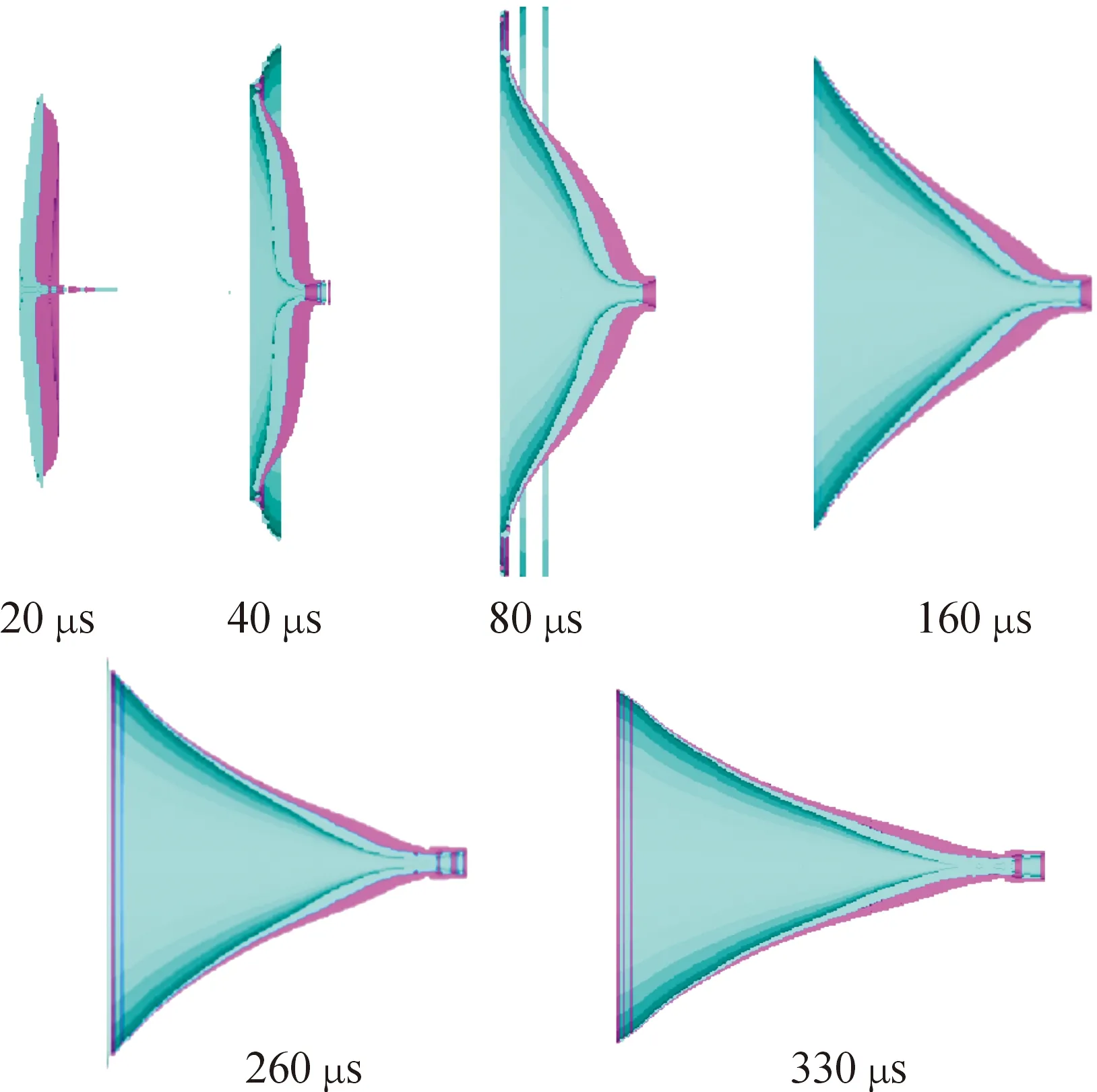
图6 方案2不同时间所形成的EFP示意图Fig.6 Scheme 2 EFP formed at different times
3.3 前后罩开孔尺寸C1>C2时
在聚能装药起爆后,初期爆轰波传播过程与方案1、方案2类似,不同的是,由于>,开孔处虽有铜随炸药向前崩落,但蹦出量极少,并且在120 μs时铜罩中心孔已经闭合,180 μs时钽罩中心孔闭合,并且在之后的拉伸中可以看出,EFP径向收缩性好,材料利用率较高,可以明显看出所形成EFP的头部直径较小。方案3为不同时间药型罩上压力分布情况,如图7所示,方案3不同时间所形成的EFP,如图8所示。
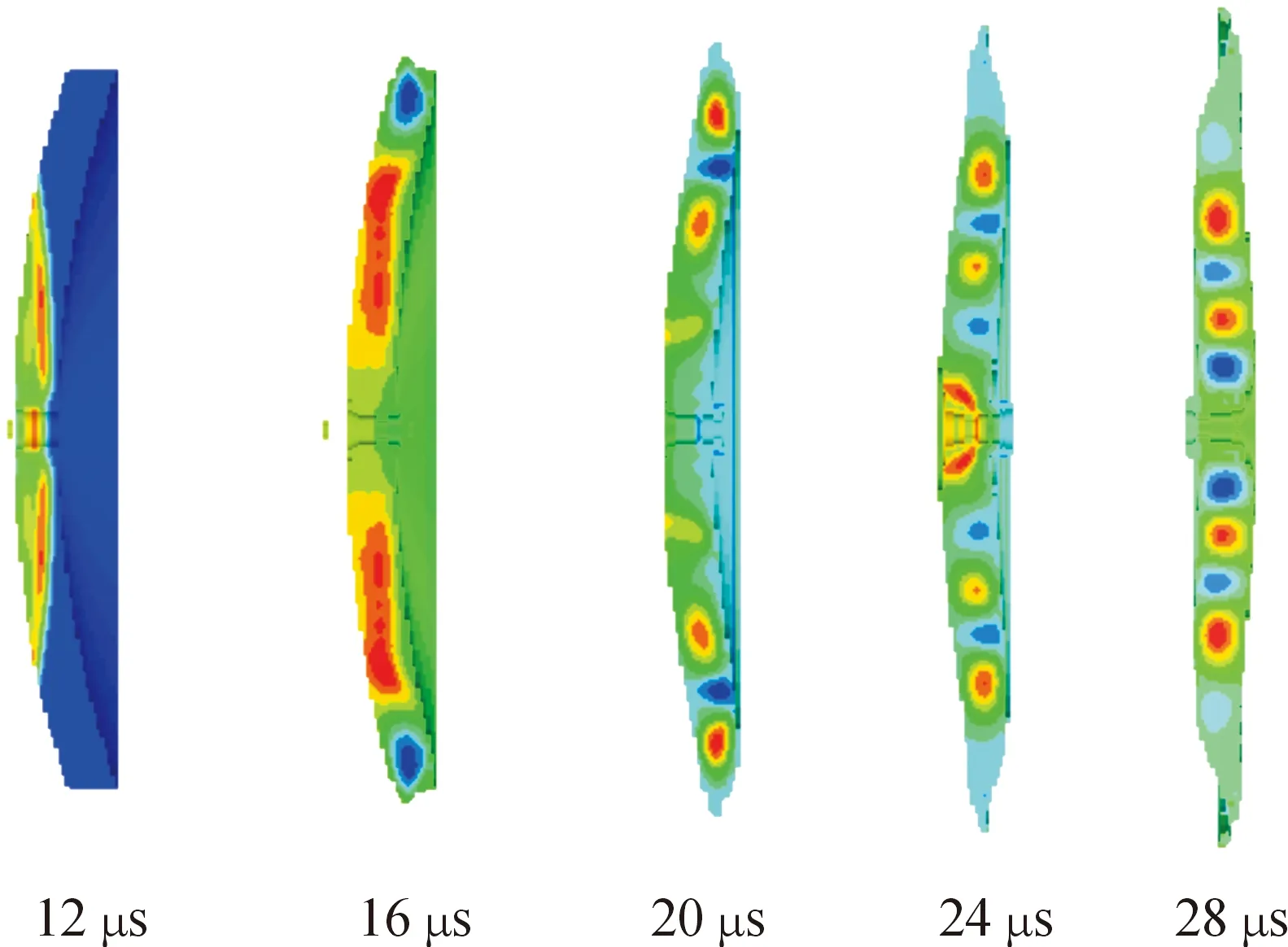
图7 方案3不同时间药型罩上压力分布情况示意图Fig.7 Scheme 3 Pressure distribution on liner at different times
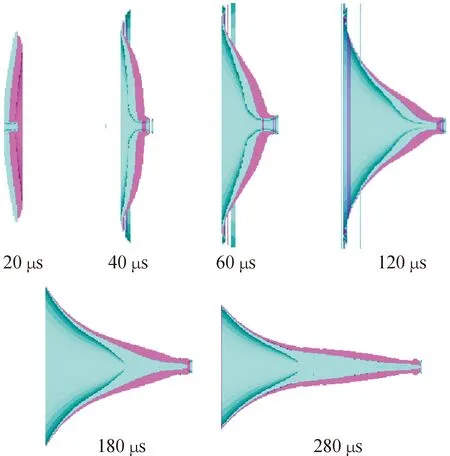
图8 方案3不同时间所形成的EFP示意图Fig.8 Scheme 3 EFP formed at different times
3.4 总体分析
中心开孔会使一部分炸药从孔中泄出,使得开孔处速度明显高于药型罩其余部分,从而增加了药型罩头部成型时的轴向速度,此时EFP的头部与尾部出现速度差,使得EFP更好地轴向拉伸,从而得到更好的长径比,同时头部直径较小,总体而言,中心开孔对药型罩EFP成型长径比影响较大。
4 装药结构优化设计
4.1 优化设计因素,水平和评定指标
分别选用长径比(),药型罩曲率半径(),壳体厚度(),两层药型罩总厚度(),和作为正交优化因素,将仿真计算得到的长径比作为评定指标,各因素以及对应的水平如表4所示。
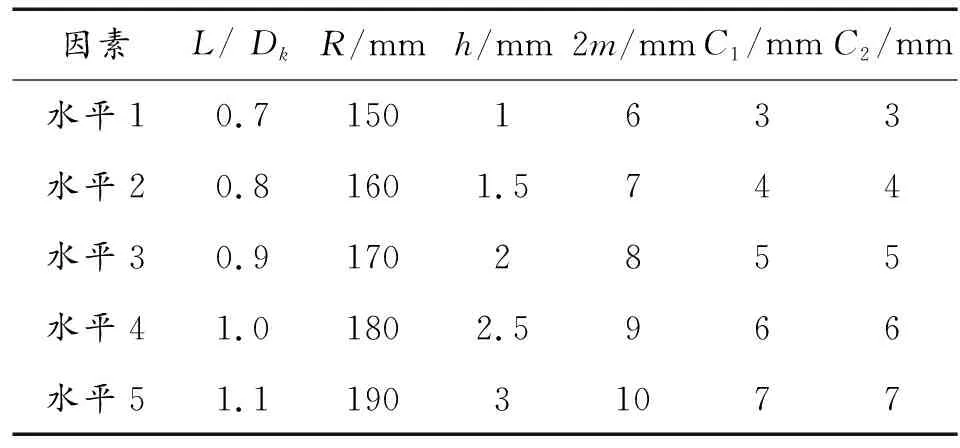
表4 正交设计各因素取值Table 4 Table of factors in orthogonal design
4.2 正交优化仿真结果
采用25(5)正交表来安排仿真方案,共计25组,结果如表5所示。
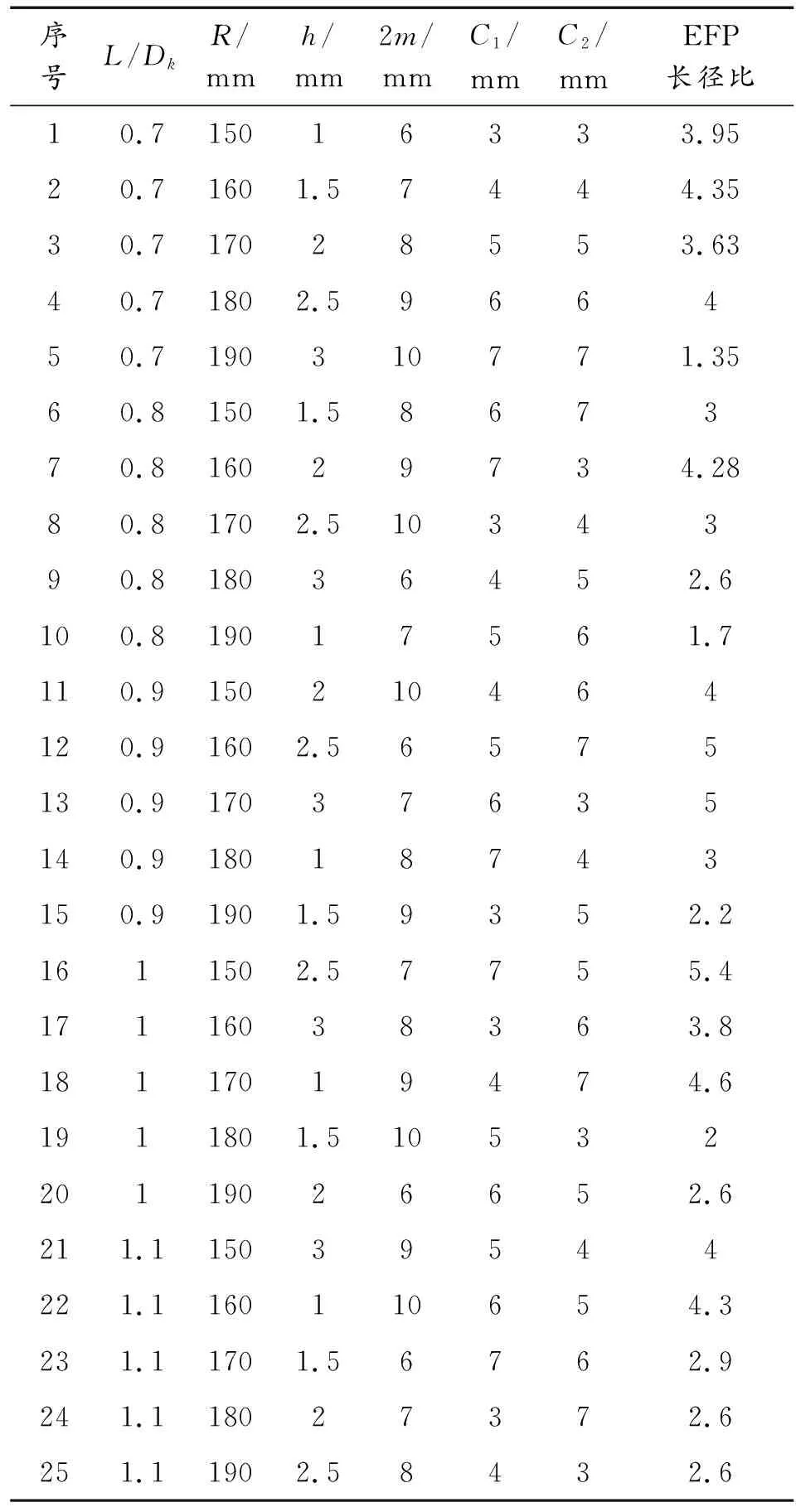
表5 正交优化仿真计算方案Table 5 Orthogonal optimization simulation calculation scheme
4.3 极差分析
分析表5数据,得出EFP极差分析结果(见表6)。
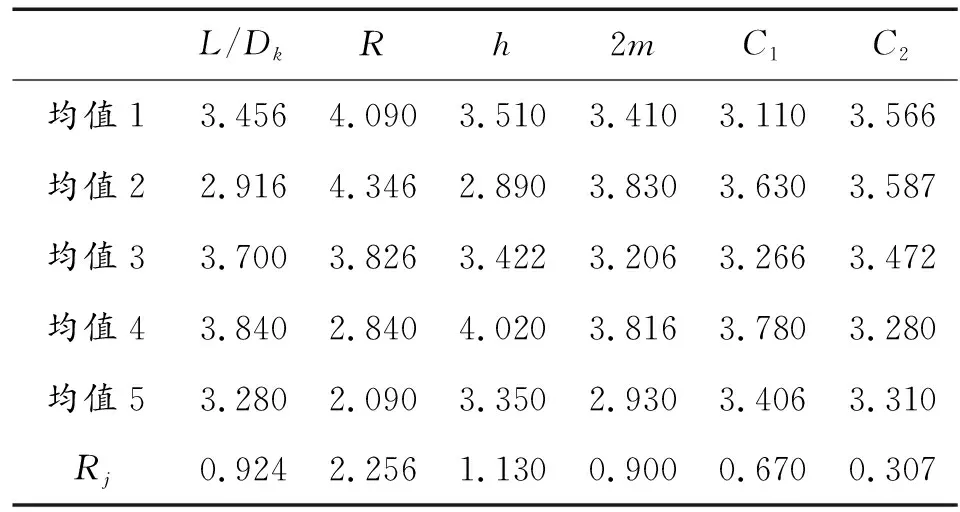
表6 EFP极差分析结果Table 6 EFP range analysis results
从表6可排列出各因素对EFP长径比的影响主次顺序,其结果显示,对所形成EFP的长径比,其影响从大到小依次为球缺罩曲率半径、壳体厚、装药长径比、药型罩总厚度、、。
综上分析,装药长径比为1,药型罩曲率半径为160 mm,壳体厚1 mm,药型罩总厚7 mm,=6 mm,=4 mm为最优装药参数。
4.4 优化方案仿真计算
本文将其与相同装药结构但中心不开孔药型罩所形成的EFP长径比进行了对比,对300 μs时成型情况进行分析,分析结果如图9所示,当中心开孔时,其形成的EFP长径比为3.0,且形成的EFP其头部相对细长;中心不开孔时,其形成的EFP长径比为2.4。相比之下,长径比提升了25%,综合分析成型情况将有利于提高战斗部的侵彻能力。
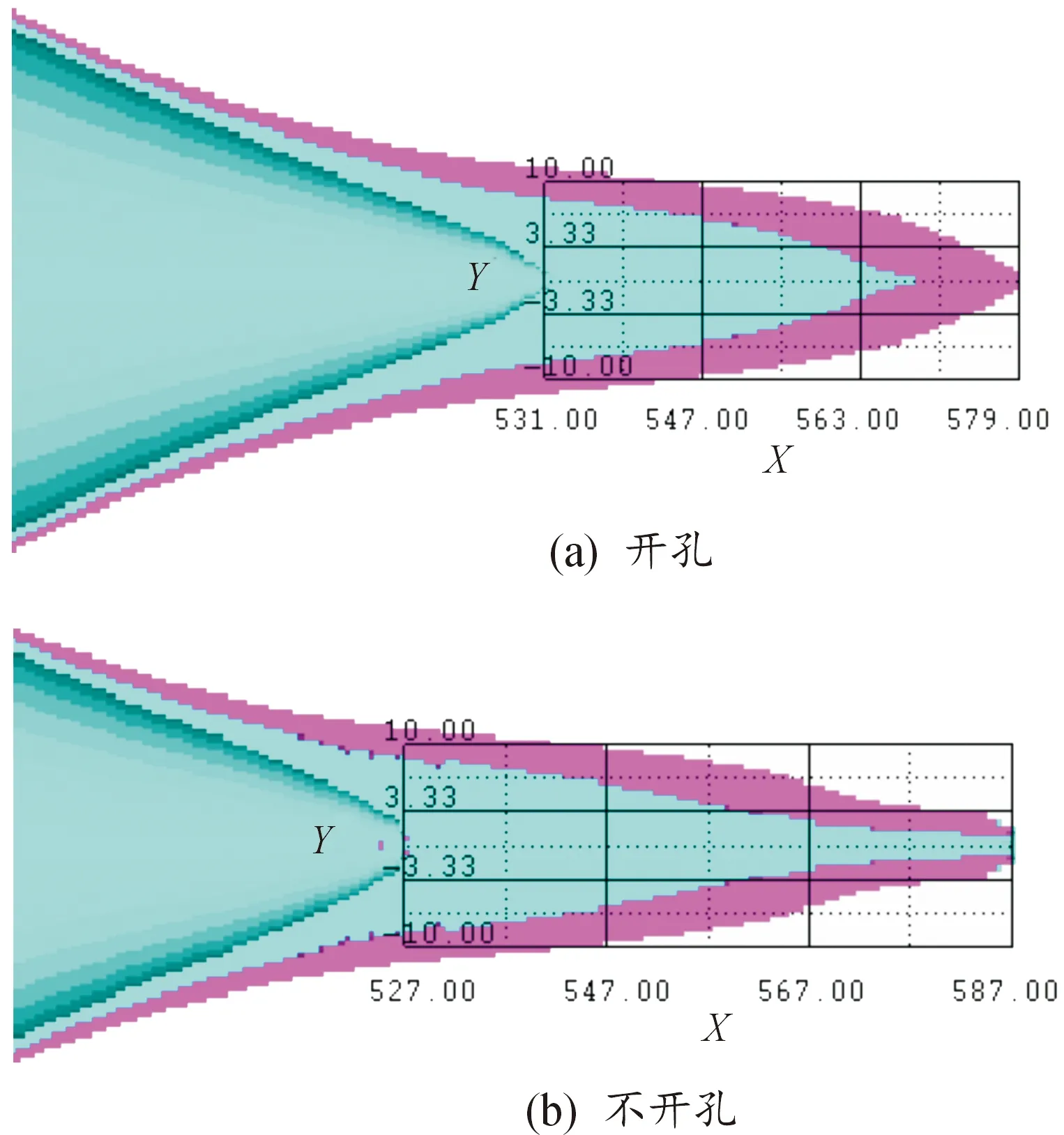
图9 300时EFP成型情况示意图Fig.9 Comparison of EFP Forming at 300 μs
5 结论
1) 对于中心带孔的等壁厚双层球缺罩,其EFP的成型情况与其两罩中心孔径大小有关。当>时,发现EFP有较优的长径比,且材料利用率较高。
2) 通过正交优化分析得出诸因素对EFP长径比影响的主次顺序为>>>>>。
3) 通过极差分析得到的最优方案,相比相同结构参数中心不开孔药型罩,在300 μs长径比提高25%,同时形成的EFP具有较细长的头部。
在聚能装药起爆后,大约8 μs后爆轰波开始作用于铜罩,铜罩在爆轰波作用下先发生变形,大约30 μs时前后药型罩所受爆轰波压力基本平均,并向后发生翻转,由于<,开孔处铜泄出量相比=时较大,在进入拉伸阶段时,铜罩与钽罩均能闭合,但EFP弹体中后部径向收缩性较差。方案2为不同时间药型罩上压力分布情况,如图5所示,方案2为不同时间所形成的EFP,如图6所示。

图5 方案2不同时间药型罩上压力分布情况示意图Fig.5 Scheme 2 pressure distribution on liner at different times

图6 方案2不同时间所形成的EFP示意图Fig.6 Scheme 2 EFP formed at different times
3.3 前后罩开孔尺寸C1>C2时
在聚能装药起爆后,初期爆轰波传播过程与方案1、方案2类似,不同的是,由于>,开孔处虽有铜随炸药向前崩落,但蹦出量极少,并且在120 μs时铜罩中心孔已经闭合,180 μs时钽罩中心孔闭合,并且在之后的拉伸中可以看出,EFP径向收缩性好,材料利用率较高,可以明显看出所形成EFP的头部直径较小。方案3为不同时间药型罩上压力分布情况,如图7所示,方案3不同时间所形成的EFP,如图8所示。

图7 方案3不同时间药型罩上压力分布情况示意图Fig.7 Scheme 3 Pressure distribution on liner at different times

图8 方案3不同时间所形成的EFP示意图Fig.8 Scheme 3 EFP formed at different times
3.4 总体分析
中心开孔会使一部分炸药从孔中泄出,使得开孔处速度明显高于药型罩其余部分,从而增加了药型罩头部成型时的轴向速度,此时EFP的头部与尾部出现速度差,使得EFP更好地轴向拉伸,从而得到更好的长径比,同时头部直径较小,总体而言,中心开孔对药型罩EFP成型长径比影响较大。
4 装药结构优化设计
4.1 优化设计因素,水平和评定指标
分别选用长径比(),药型罩曲率半径(),壳体厚度(),两层药型罩总厚度(),和作为正交优化因素,将仿真计算得到的长径比作为评定指标,各因素以及对应的水平如表4所示。

表4 正交设计各因素取值Table 4 Table of factors in orthogonal design
4.2 正交优化仿真结果
采用25(5)正交表来安排仿真方案,共计25组,结果如表5所示。

表5 正交优化仿真计算方案Table 5 Orthogonal optimization simulation calculation scheme
4.3 极差分析
分析表5数据,得出EFP极差分析结果(见表6)。

表6 EFP极差分析结果Table 6 EFP range analysis results
从表6可排列出各因素对EFP长径比的影响主次顺序,其结果显示,对所形成EFP的长径比,其影响从大到小依次为球缺罩曲率半径、壳体厚、装药长径比、药型罩总厚度、、。
综上分析,装药长径比为1,药型罩曲率半径为160 mm,壳体厚1 mm,药型罩总厚7 mm,=6 mm,=4 mm为最优装药参数。
4.4 优化方案仿真计算
本文将其与相同装药结构但中心不开孔药型罩所形成的EFP长径比进行了对比,对300 μs时成型情况进行分析,分析结果如图9所示,当中心开孔时,其形成的EFP长径比为3.0,且形成的EFP其头部相对细长;中心不开孔时,其形成的EFP长径比为2.4。相比之下,长径比提升了25%,综合分析成型情况将有利于提高战斗部的侵彻能力。

图9 300时EFP成型情况示意图Fig.9 Comparison of EFP Forming at 300 μs
5 结论
1) 对于中心带孔的等壁厚双层球缺罩,其EFP的成型情况与其两罩中心孔径大小有关。当>时,发现EFP有较优的长径比,且材料利用率较高。
2) 通过正交优化分析得出诸因素对EFP长径比影响的主次顺序为>>>>>。
3) 通过极差分析得到的最优方案,相比相同结构参数中心不开孔药型罩,在300 μs长径比提高25%,同时形成的EFP具有较细长的头部。
