智能分布式武器装备系统寿命估计方法研究
2022-10-14赵爱罡钟建强孙兴奇许倍榜李瑞帅
赵爱罡,葛 春,钟建强,孙兴奇,许倍榜,寇 峰,李瑞帅
(火箭军士官学校, 山东 青州 262500)
1 引言
随着科技的快速发展,出现了多种智能化武器装备。为挖掘武器系统的潜能,使武器系统尽可能发挥作用,需要对这种智能分布式可重复使用的群系统建立寿命预测与可靠性研究,为作战决策提供技术支撑。每个单体均是独立的智能体,包含传感器、执行机构、控制器等关键部件,并且需要的数量较多,武器装备系统又由多个单体组成,为方便研究,将日常的测试项目及数据进行分析,按照对关键部件寿命的影响大小,选择重要测试数据进行归一化为综合性能指标,对关键部件的退化规律进行研究,建立时间序列模型,对综合性能指标进行预测,最后对所有关键部件进行统计分析,拟合全寿命概率分布,计算武器系统的可靠性。
近年来,关于寿命预测方法主要有GM(1,1)、ARIMA、支持向量机、极端学习机(extreme learning machine, ELM)、深度学习等,ARIMA模型对时间序列有一定的要求,要符合平稳性,GM(1,1)模型本质为指数模型,预测效果依赖于数据规律,支持向量机模型对线性规律预测较好,预测精度与数据规律有关,ELM模型能够处理非线性预测,但是预测精度是建立在训练数据基础之上的。Peng等尝试使用卷积神经网络(convolutional neural network, CNN)来进行预测估计, 使用时间窗口对原始数据进行滤波, 使得CNN能够提取特征,在多通道上应用卷积和池化滤波器,提出基于卷积神经网络的回归方法来预测寿命。Wang等利用深度学习理论与相似性曲线匹配算法估计系统的寿命,使用双向长短期记忆网络(Bi-directional long short-term memory, Bi-LSTM)进行无监督学习, 最后利用相似性匹配算法对健康指数值进行匹配, 进而实现航空发动机的剩余寿命预测。
深度学习需要大量的样本数据,且训练耗时,而且对趋势外推预测效果不佳。基于此,观察综合性能指标曲线有明显指数趋势,所以拟采用GM(1,1)对趋势进行预测,采用训练简单、快速收敛的ELM模型对其预测残差进行预测,最后合成预测结果,经过数据验证,满足寿命预测的精度要求。
2 急速退化期识别
某武器装备系统包含某类关键部件共235个,正常使用情况下,间隔15 d对关键部件进行一次测试,将测试数据分析,形成综合性能指标。当综合性能指标大于0.69时,随机挑选3个关键部件的综合性能指标全寿命曲线,如图1所示。曲线变化特点相似,有以下几个特点:

图1 随机抽取关键部件全寿命曲线Fig.1 Randomly extract the full life curve of key components
1) 前半段为正常使用期,初始值设为0.2,随后在[0.1,0.3]振荡;
2) 综合性能指标在某点之后,进入急速退化期,综合性能指标快速升高;
3) 在急速退化期,是逐步、连续、非均匀退化的,综合性能指标退化步长有限,没有出现大的跳跃,但在某些点呈现降低的现象。寿命终止。
经过以上分析,决定关键部件寿命的是急速退化期,所以需要识别每个关键部件的急速退化期,简化模型的预测难度。
根据综合性能指标的变化特点,如图2所示,采用如下方法识别急速退化期:
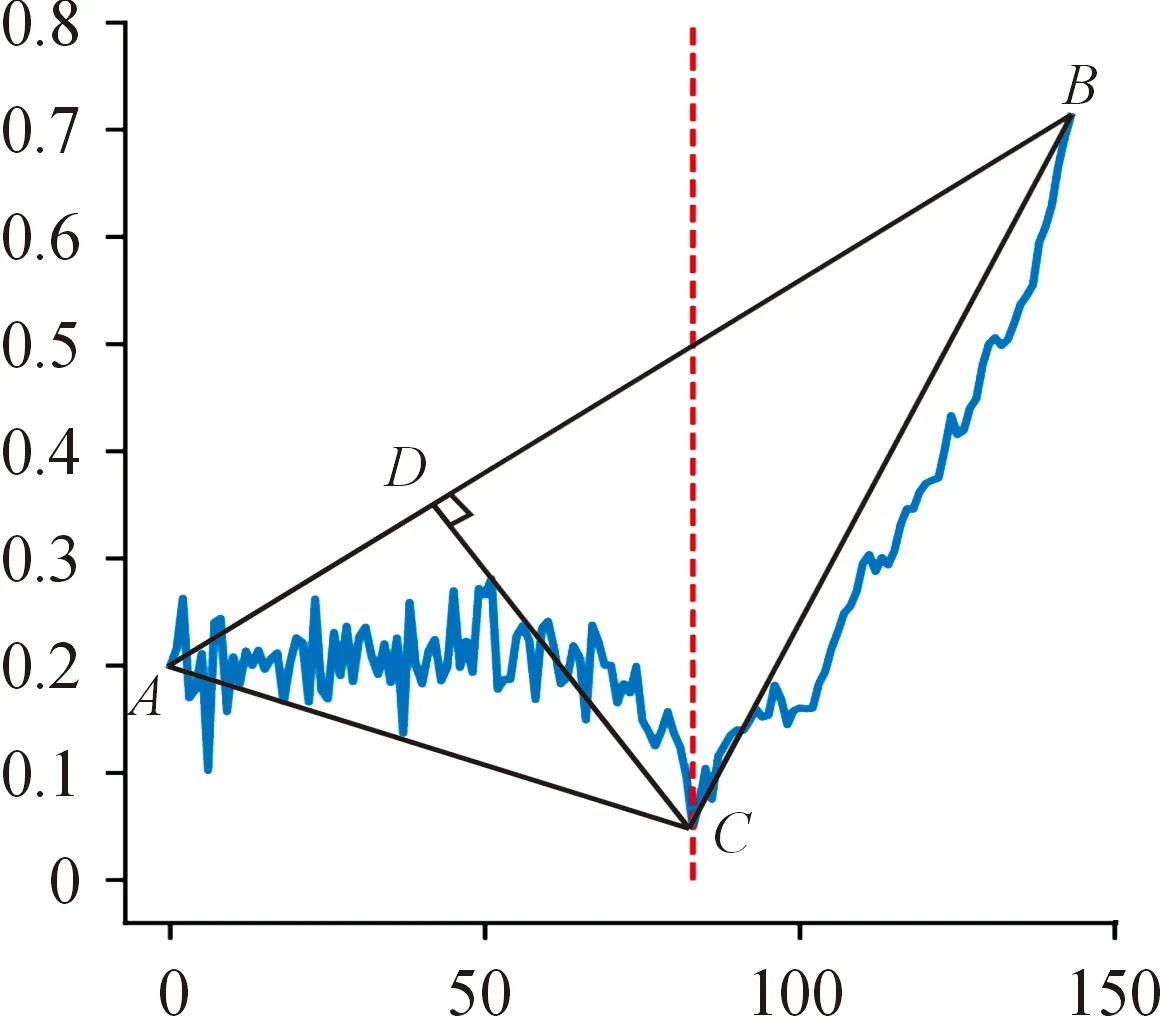
图2 急速退化期识别曲线Fig.2 Rapid degeneration identification
1) 选取终点。当综合性能指标大于04时,任取一点为点,坐标为(,);
2) 计算任一点面积。计算三角形的面积,其中点为起点,坐标为(0,02),点为综合性能指标曲线上的任一点,坐标为(,),则计算公式为:

(1)
3) 确定面积最大的点。在综合性能指标曲线上找到面积最大的点,作为正常使用期与急速退化期的分界线,段即为急速退化期。
在图1与图2中,按上述方法识别的急速退化期,图中竖虚线表示,可以看出3个关键部件的急速退化期起始点的综合性能指标均处于0.3以下,确保了关键部件的使用可靠性,急速退化期趋势明显。
3 关键部件寿命预测
3.1 GM(1,1)模型
GM(1,1)是一次累加的一阶微分方程模型,其解是一种指数函数,适用于数据量较少的短时预测。模型构建需要3个步骤,首先对数据的变换步长进行检验,确保其累加和能够使用微分方程形式来描述,本质为指数模型。其次求解模型3个未知参数,定量描述数据,最后根据评价标准评估模型的精度,并对新数据进行预测。
1) 数据变化步长检验
设非负时间序列如下:
={(1),(2),…,()}
(2)
式中:为序列长度,若序列满足如下范围:

(3)
说明时间序列累加和能够使用指数模型来描述,可使用GM(1,1)对其进行预测,若不满足检验标准,则可对原序列进行变换,如取对数运算,加常数等,使得时间序列的步长相对减小,能够满足检验标准。
2) 模型参数估计
时间序列累加和序列定义为:
={(1),(2),…,()}
(4)

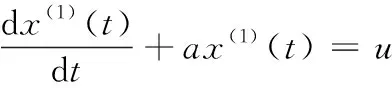
(5)
式中,称为发展系数,正负号分别表示序列的衰减和增加,绝对值大小反映了序列变化的快慢,非齐次项为灰色作用量,反映了序列偏移量的大小。
将式(5)的连续形式变为离散形式,式(5)两侧同时积分,积分区间为[-1,],公式变为:
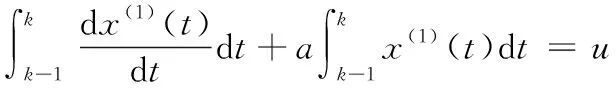
(6)
上式中的第二项的几何含义为函数()与横轴围成的面积,这里称为背景值,为简化计算,近似为梯形计算面积,公式为:
()=05(-1)+05()
=2,3,…,
(7)
式(6)中的第一项积分后为序列的原始值,结合式(7),式(6)可写为:
()+()=
(8)
根据时间序列的长度,可组成-2个方程,共有2个未知数,通过最小二乘计法计算和为:
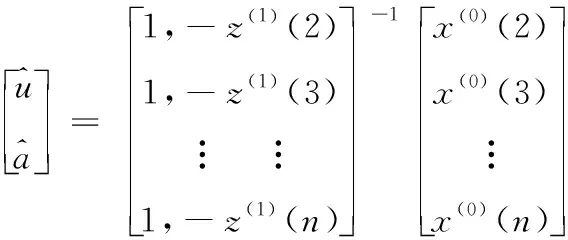
(9)
因为微分方程(5)的通解为:
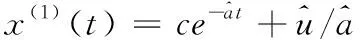
(10)
其中,为待定系数,因(1)=(1),代入式(10)计算为:

(11)
至此,式(10)3个参数已知,通过序列作差可得到原序列的解析解,公式为:
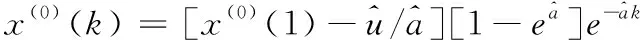
(12)
GM(1,1)模型已建立,通过取不同值,可以对原序列进行拟合和预测。
3.2 ELM模型
ELM本质是单隐层神经网络,相比传统的BP神经网络,将参数训练的迭代调整过程转化为随机生成前置网络权值和求解线性方程组,降低了训练过程中参数调节难度,通过最小二乘求得后置网络权值,整个训练过程无需迭代, 这使得ELM的训练速度显著提升。
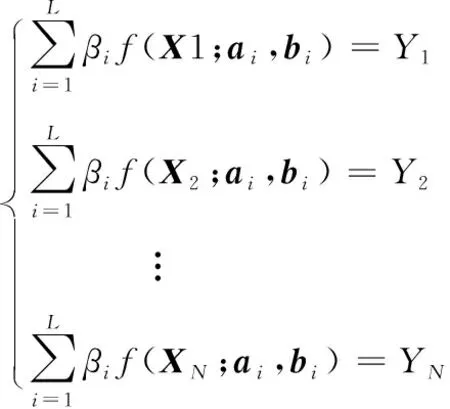
(13)

β=
(14)
式中:为神经元矩阵;为输出向量;为输出权值。其值分别为:

(15)
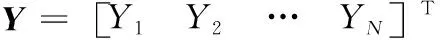
(16)
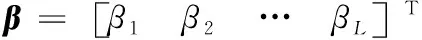
(17)
一般情况下,隐层神经元数目小于训练样本数目,即<,此时是非方阵,无法直接求逆矩阵,根据广义逆引理,上述线性系统的最小范数二乘解为:
=
式中,为矩阵的广义逆。
结合上述推导,给定一个训练样本集,激活函数为(),隐层神经元数目为,ELM模型的求解步骤为:
1随机指定输入权值和隐层神经元偏置系数,=1,2,…,;
2计算隐层输出矩阵;
3计算输出权值,为避免病态矩阵出现伪逆计算错误,加入正则化参数,可避免伪逆无法计算的问题,=(1+)。
3.3 GM(1,1)-ELM模型
基于上述GM(1,1)和ELM模型,对关键部件的综合性能指标采用GM(1,1)-ELM模型进行预测,如图3所示。首先使用GM(1,1)对数据进行拟合,因为GM(1,1)为解析的指数模型,曲线较为平滑,能够捕捉并预测数据序列的趋势变化,但是综合性能指标数据一般较为复杂,只依靠指数模型预测精度不能满足要求。于是对GM(1,1)的预测残差进行分析发现,残差是一平稳序列,存在自相关性,具有可预测的可能,所以对GM(1,1)的预测残差使用ELM模型进行预测,并将预测结果合并,进一步提高模型的预测精度。

图3 GM(1,1)-ELM模型流程框图Fig.3 GM(1,1)-ELM model flow chart
这种结合方式融合了GM(1,1)模型的趋势预测和ELM非线性预测的优势,弥补了GM(1,1)预测精度不足与ELM模型不擅长外延预测的劣势。
4 实验验证及结果分析
为验证GM(1,1)-ELM模型效果,随机抽取3、131、202号关键部件的综合性能指标,将序列急速退化期的后3个测试数据作为验证数据,使用前面数据建立模型。
1) GM(1,1)模型结果
3个时间序列均能够通过式的检验,建立模型表达式分别为:

(19)

(20)

(21)
以上为3个关键部件的综合性能指标的预测表达式。
图4为131关键部件综合性能指标GM(1,1)模型的预测曲线,每条曲线的后3个数据为验证数据,可直观看出GM(1,1)模型预测曲线能够平滑地捕捉样本真值的趋势,确保未来数据预测趋势一致性。
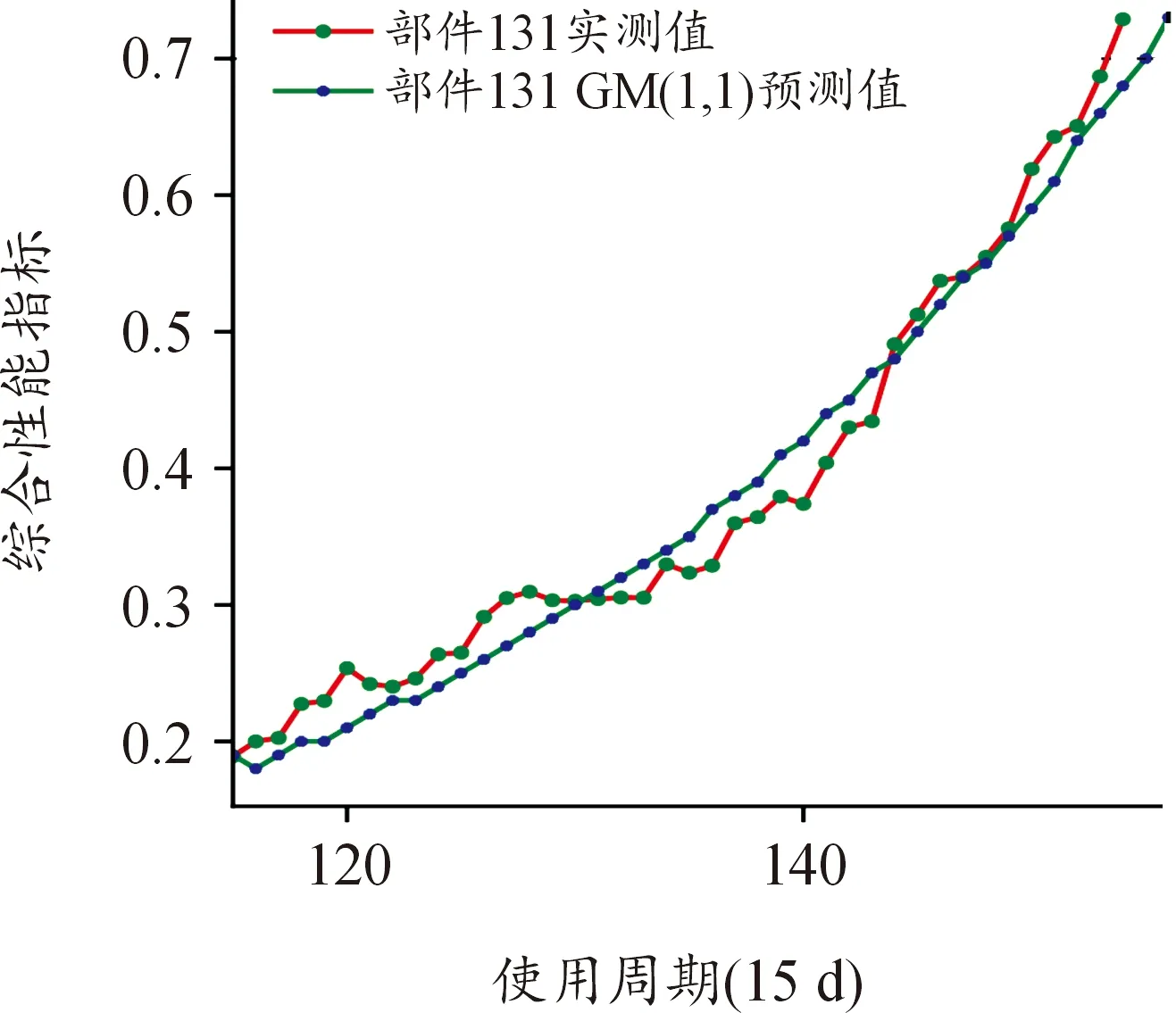
图4 131号关键部件GM(1,1)模型预测曲线Fig.4 Prediction results of GM(1,1) model for key component No.131
2) ELM模型结果
对GM(1,1)的预测结果剩余残差进行ELM预测,ELM模型需要设置的参数有:嵌入维大小、神经元数量、神经元种类。ELM属于单隐层神经网络,原理上嵌入维越大、神经元数量越多拟合效果越好,但是会导致过拟合现象,预测效果下降较快,所以选择合适的参数比较重要。
在本例中,神经元类型选择常用的正切sigmoid函数,以平均误差的下降比例为目标函数,在一定范围内,遍历嵌入维和神经元数量,当平均误差的下降比例大于0.8时,确定嵌入维及神经元数量。3号、131号、202号关键部件的嵌入维分别为:7、6、5,神神经元数量分别为:28、15、17。如图 5所示为3号关键部件的GM(1,1)模型预测残差的ELM预测结果。
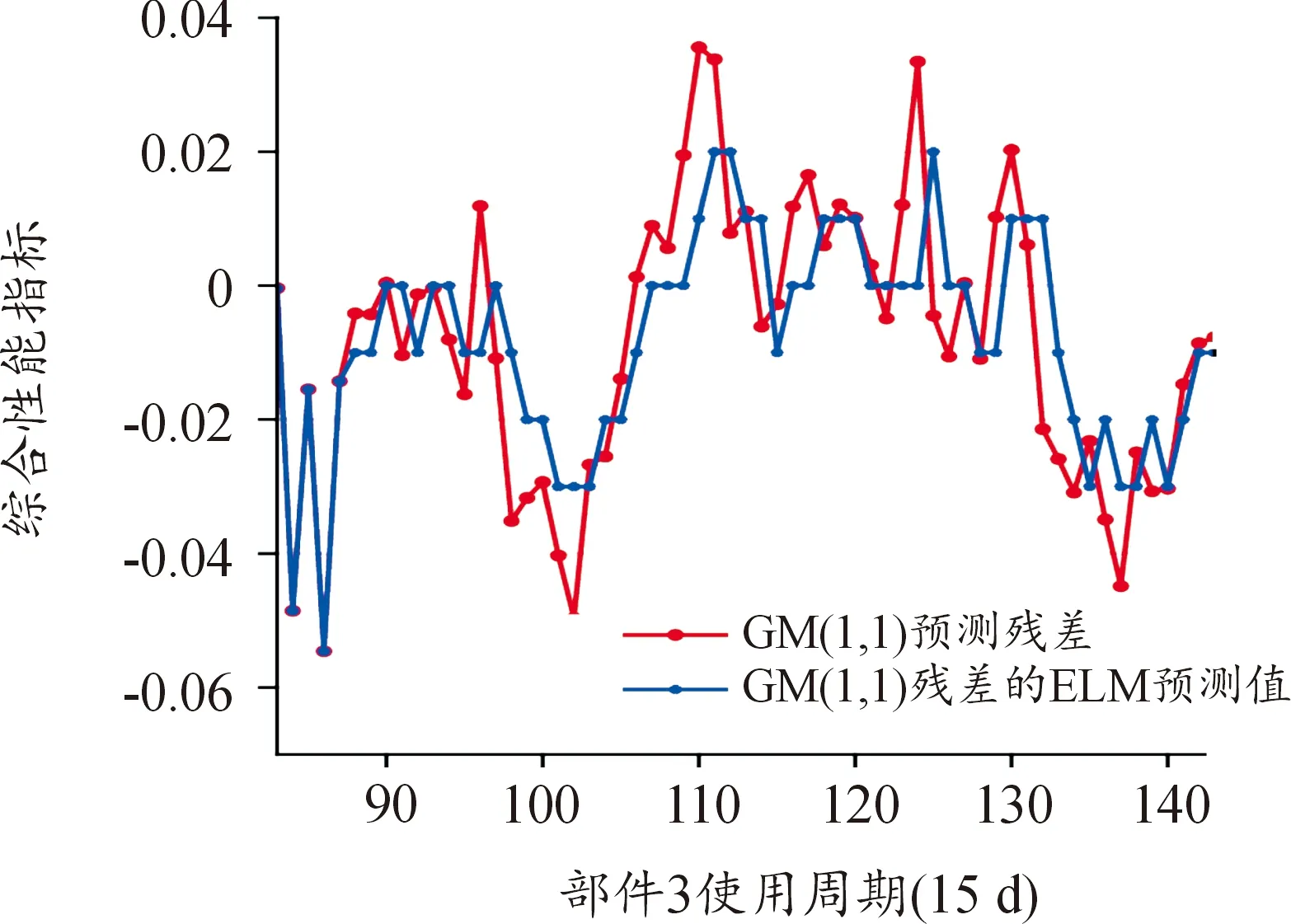
图5 3号关键部件GM(1,1)预测残差的ELM预测曲线Fig.5 ELM prediction results of the prediction residuals of the GM(1,1) model for key component No.3
由图5可以看出,GM(1,1)模型预测残差在0值上下波动,波动范围在[-0.05,0.04]区间内,ELM模型可以短时捕捉变化规律,在0值附近预测效果较好,在极限值处预测误差较大,这种预测效果会起到对原序列的平滑作用,注重序列趋势的精确预测。
3) GM(1,1)-ELM模型结果
图6为3号和131号关键部件综合性能指标3种模型预测曲线。图6为局部放大的效果,对数据序列直接使用ELM模型进行预测,预测精度比GM(1,1)模型略高,但是对于预测未知数据,训练数据无法覆盖,难以确保对外延数据的预测性能,而GM(1,1)模型虽然预测精度略差,但是能够保证数据序列趋势预测的正确性。GM(1,1)-ELM模型以GM(1,1)模型预测为主体,使用ELM模型预测残差提高精度,因为残差主要分布在0值附近的,数据完备,所以ELM模型对于非全寿命数据序列的预测,其训练数据也是可以全覆盖的,能够显著提高预测精度。
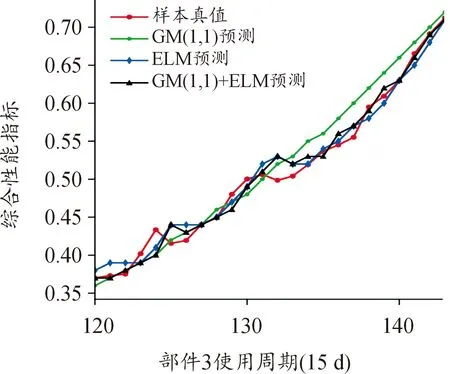
图6 3号关键部件3种模型的预测结果曲线Fig.6 Prediction results of three models for key component No.3
表1为3个模型对3个序列预测平均相对误差,红色标记为最小平均相对误差,可以看出GM(1,1)-ELM模型具有较好的表现,预测精度显著提高。
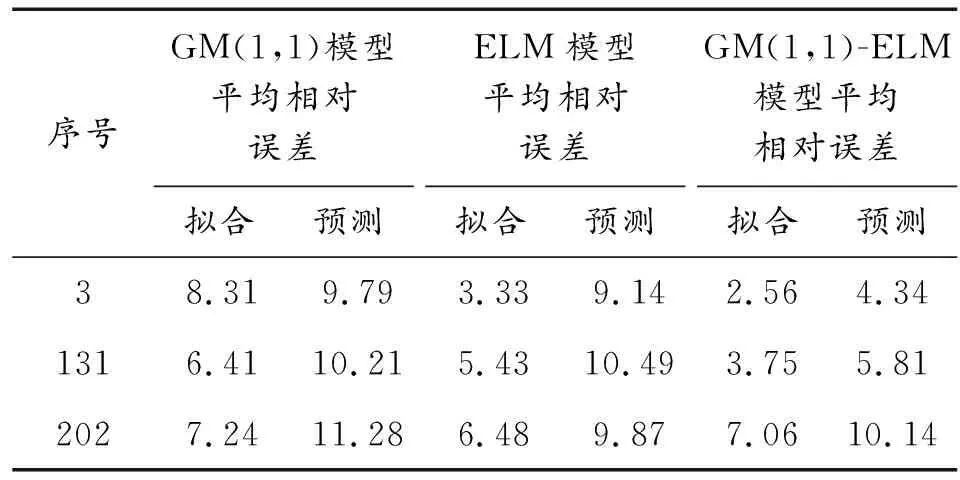
表1 3种模型平均相对误差对比Table 1 Comparison of the average relative errors of the three models
5 武器装备系统寿命估计
如图7所示,首先对综合性能指标未达0.69的关键部件使用GM(1,1)-ELM模型进行预测,为提高预测的可靠性,暂时预测3步,对所有关键部件寿命按0.69进行统计,假设235个关键部件的综合性能指标预测结果均在0.69以上,则根据统计量画出直方图,对参数进行估计,计算寿命的概率密度函数,根据标准,估计智能分布式武器装备系统的寿命。

图7 智能武器装备系统寿命估计流程框图Fig.7 Flow chart of life estimation of intelligent weapon equipment system
记录每个样本的综合性能指标大于0.69时的检测次数,次数减1即为寿命,计算公式如下:
()=inf{-1|,≥069},∈[1,235]
式中:()为样本的寿命;, 为第个样本第次测量的综合性能指标。图8所示为235个关键部件的寿命,可以看出寿命集中在120~130和140~150,最小寿命为样本序号为84的112个寿命周期,最长寿命为样本序号为129的161个寿命周期。

图8 235个关键部件的全寿命曲线Fig.8 Full life of 235 key components
首先将寿命跨度平均分为40份,计算每个区间内样本的数量,最后除以样本总数,即为在寿命范围内样本所占的比例,如图9为235个样本的全寿命直方图。
由图9可以看出,其概率密度分布是有2个中心的,具有2个峰值,经过高斯模型与多项式模型的对比发现,多项式模型涉及参数较多,结构复杂,所以选择双重高斯模型,其表达式为:
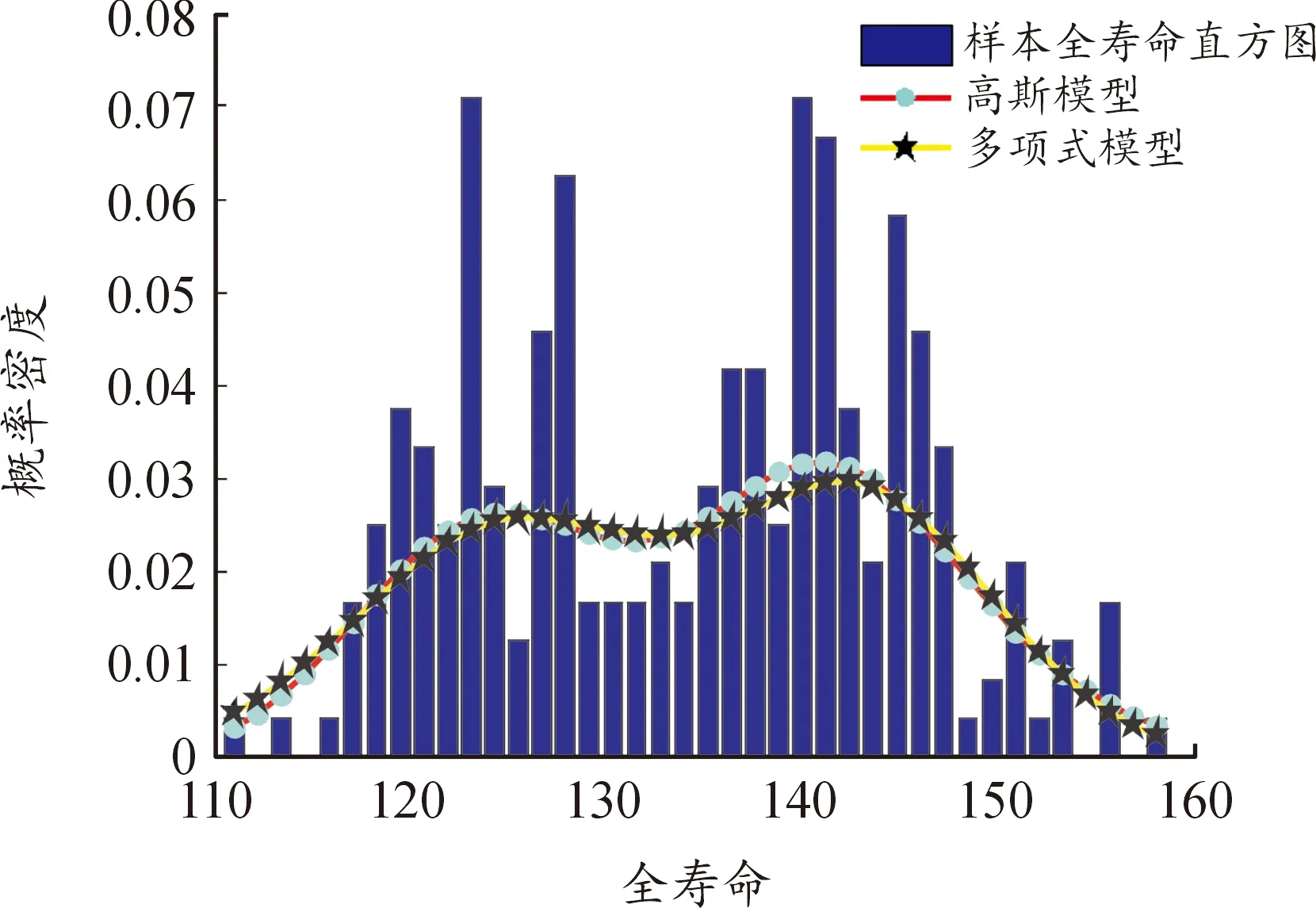
图9 武器装备系统的寿命概率密度直方图Fig.9 Life probability density of weapon system
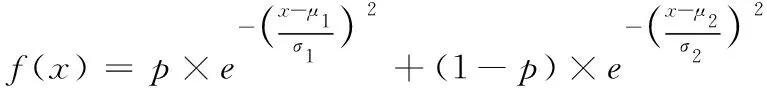
(23)
式(23)为简化版的双重高斯分布模型,为寿命,为比例系数,、、、分别为均值和标准差,共有5个参数,利用最小二乘法对参数进行估计,模型表达式为:

(24)
当没有关键部件损毁时,武器装备系统状态优良,评定为一级状态,当有小于等于20%的同类关键部件损毁时,武器装备系统可正常使用,评定为二级状态。当有大于20%小于等于35%关键部件损毁时,武器装备系统的性能逐渐降低,但是基本可以使用,评定为三级状态。当大于35%的关键部件损毁时,评定为不合格,武器装备系统寿命终止。
图10为智能分布式武器装备系统寿命概率分布曲线。蓝色区域对应20%的关键部件损毁,红色区域对应35%关键部件损毁。所以一级状态寿命区间为:[0,112],二级状态寿命区间为:[113,123],三级状态寿命区间为:[124,130],超过130个检测周期,武器装备系统无法使用,需要尽快更换关键部件。
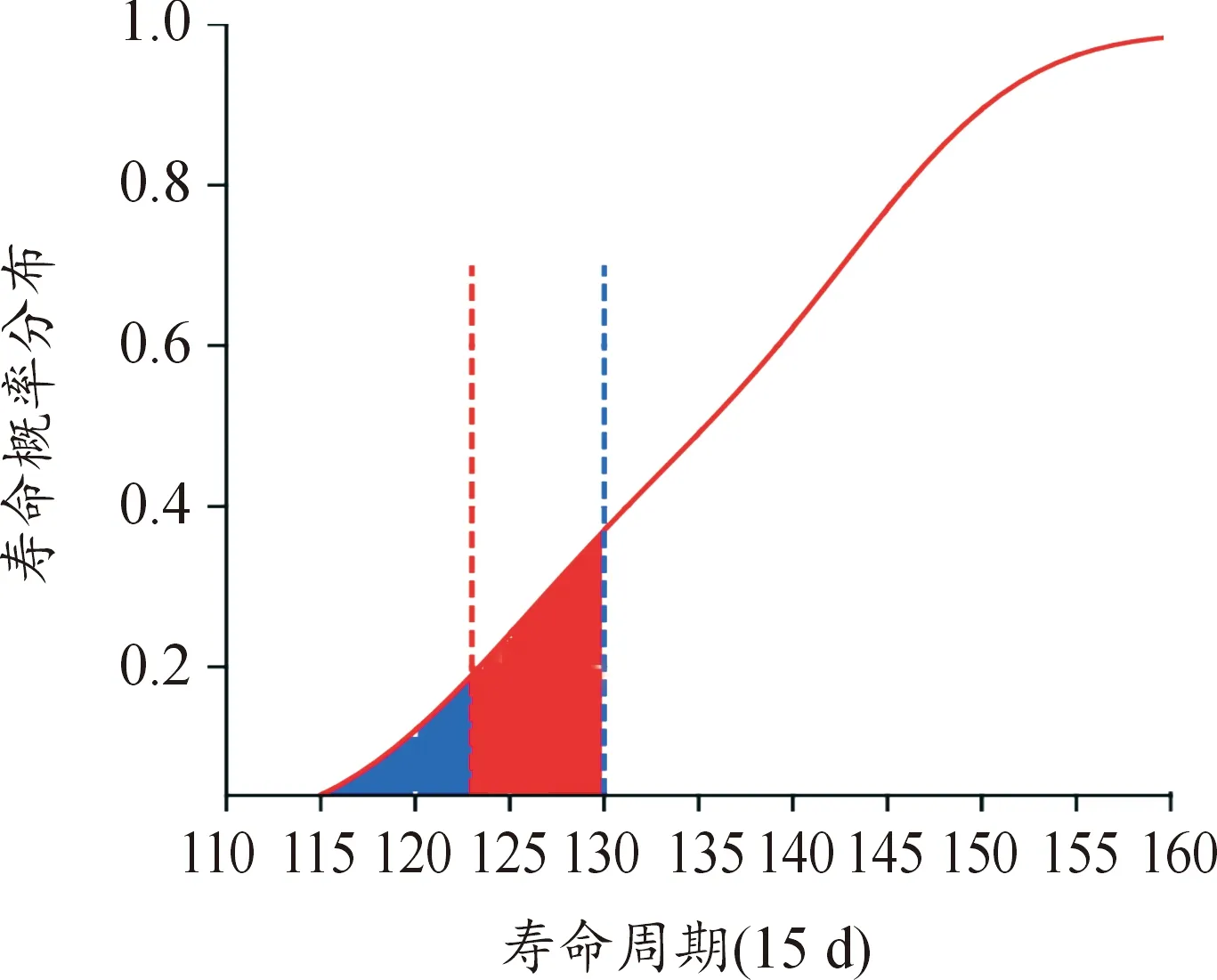
图10 武器装备系统寿命概率分布曲线Fig.10 Probability distribution of lifespan of weapon equipment system
6 结论
1) 对智能化分布式武器装备独立系统或部件寿命进行科学预测,确定部件寿命与系统寿命之间的关系,能够帮助使用者掌握复杂系统状态,提高装备维护使用效率。
2) 针对GM(1,1)模型预测精度不高,ELM模型训练数据不完备的问题,采用GM(1,1)模型捕捉数据序列的趋势,ELM模型以GM(1,1)预测残差为训练数据,两者融合的GM(1,1)-ELM模型确保了预测的可靠性和预测精度。
3) 利用GM(1,1)-ELM对多个关键部件的综合性能指标进行预测验证,与单独使用GM(1,1)模型相比,预测精度显著提高,可进行关键部件精准寿命预测。
4)基于关键部件的全寿命周期,采用双重高斯模型拟合寿命概率密度,按照指标计算智能化分布式武器装备系统的寿命区间及状态,可为日常维护使用提供数据支撑。
