基于深度强化学习的无人艇集群博弈对抗
2022-10-14刘殿勇
苏 震,张 钊,陈 聪,刘殿勇,梁 霄
(1.珠海云洲智能科技股份有限公司 工业发展部, 广东 珠海 519080;2.大连海事大学 船舶与海洋工程学院, 辽宁 大连 116026)
1 引言
水面无人艇作为智能化无人系统和作战平台的代表性武器装备,具有体积小、造价低、隐身性好、全海域航行、全天候工作等特点,能够在环境调查、情报侦查、警戒巡逻、反水雷作战等领域发挥重要作用。
在复杂多变的海洋环境下,单无人艇载荷配置十分有限、任务能力偏弱、作战样式相对单一,在很大程度上无法保证任务的顺利完成。无人艇集群协同作战可弥补单艇能力的不足,充分发挥群体灵活部署快、监控范围广、作战组织灵活、抗毁重构性强等优势。为应对无人艇集群攻击,最有效的方法就是利用无人艇集群对入侵的无人艇集群进行拦截、驱离或围捕,从而形成无人艇集群间的博弈对抗。
博弈对抗技术是智能化军事应用的基础和共性技术,是解决指挥控制中作战方案生成、任务规划及临机决策等智能化的关键,同时也是训练模拟、自主集群无人化作战等军事关键领域智能化建设的核心技术基础。因此,在网络环境下,研究无人艇集群博弈对抗技术具有重要的理论意义和军事价值。
Marden等研究了基于博弈理论的协同对抗技术,通过评估当前行为的后续影响,以及对可能发生的情况进行预测估计,从而制定更为合理的实时方案。Atanassov等对传统模糊集进行了进一步拓展,由于直觉模糊数的二元标量性具有更强的模糊表述能力,被广泛地应用于解决不确定环境下的决策问题。Park等基于微分博弈理论,提出了一种机动决策方法,遵循分级决策结构,使用评分函数矩阵描述机动决策过程,以选择动态作战态势下最优机动决策方案,提升机动决策的有效性。邵将等通过建立多无人机协同空战连续决策过程,使用贝叶斯推论对空战态势进行实时评估,并以此设计的决策规则进行机动决策。陈侠等通过建立无人机的能力函数,建立多无人机协同打击任务的攻防博弈模型,给出了有限策略静态博弈模型与纯策略纳什均衡的求解方法。通过求解博弈模型的混合策略纳什均衡解,并结合一定作战经验,形成任务决策方法。段海滨等研究了“狼群”智能行为机理,并将其应用于无人机集群系统对抗任务,解决无人机集群协同决策问题。魏娜等针对多自主水下航行器的水下协同对抗博弈问题,以博弈论为基础,多无人艇的多次对抗为作战背景,从同时考虑敌我双方对抗策略的角度出发,对多无人艇的动态协同攻防对抗策略问题进行了研究。李瑞珍等采用协商法为机器人分配动态围捕点,建立包含围捕路径损耗和包围效果的目标函数并优化 航向角,从而实现协同围捕。陈亮等提出混合DDPG算法,有效协同异构agent之间的工作,同时,Q函数重要信息丢失及过估计等问题有待解决。Foersteret提出了使用集中式评论家的 COMA,集中式评论家可以获得全局信息来指导每个智能体,从而进一步提高每个智能体的信息建模能力。
上述研究成果的取得表明国内外研究学者在无人艇集群博弈对抗方面取得了一定的研究成果,但仍处于起步阶段,存在许多实际问题有待进一步解决。
第一,无人艇集群动态博弈对抗研究较少。海上博弈对抗环境复杂且目标大都为动态,动态对抗在决策过程中不仅需要考虑博弈前一阶段的影响,同时需考虑对后一阶段产生的后果。
第二,实时决策效率较低。无人艇集群动态博弈对抗过程中,每个阶段均需通过多步矩阵运算产生对抗双方的博弈收益,这将导致博弈空间复杂度成指数级增长,现有求解算法难以实现实时决策目的。
本文中针对红蓝双方无人艇集群动态博弈对抗问题,开展基于深度强化学习的无人艇集群协同围捕决策研究。首先,根据无人艇集群状态信息与无人艇运动性能进行围捕环境建模;然后,采用基于双评价网络改进的DDPG算法设计策略求解方法,并且立足协同围捕任务,设计基于距离和相对角度的阶段性奖励函数;最终,经仿真实验验证,训练得到的智能体能够较好的完成协同围捕任务。
2 问题描述
无人艇集群协同围捕是集群作战的典型样式,在无限大且无障碍的作战区域内,存在若干艘逃逸无人艇与围捕无人艇,逃逸无人艇要在躲避围捕无人艇追踪;围捕无人艇要对逃逸无人艇尽快完成对其的围捕。本文中追击-逃逸过程在二维平面内进行,且假设通过探测设备,双方均能获得所有无人艇运动参数信息。
红方无人艇的目标点均匀分布在以蓝方艇群中心为圆心,以为半径的圆上。此外,考虑到无人艇机动性,若各红方艇距离目标点均小于时,可视为围捕完成。以5艘围捕无人艇,一艘逃逸无人艇为例,围捕过程如图1所示,围捕完成如图2所示。

图1 围捕过程示意图Fig.1 Round up process

图2 围捕完成示意图Fig.2 Round up complete
无人艇运动模型为
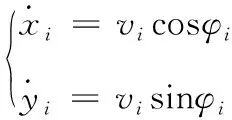
(1)
式中:表示第艘无人艇横向位置;表示无人艇纵向位置;表示无人艇速度大小;表示无人艇艏向角。
第艘无人艇与第艘无人艇相对距离和相对角度为

(2)
状态空间包括各无人艇位置信息,其具体形式为
=(,,,,…,,,,)
(3)
无人艇动作空间是连续的,对应的动作为二维速度向量。定义蓝方无人艇速度大小∈[0,max],max为蓝方无人艇速度上限;艏相角∈[0,2π](单位为弧度);定义红方无人艇速度大小∈[0,max],max为红方无人艇速度上限;艏相角∈[0,2π]。
3 集群博弈对抗策略
本文中基于改进的深度确定性策略梯度(deep deterministic policy gradient,DDPG)算法研究无人艇集群博弈对抗策略问题,DDPG算法结构如图3所示。
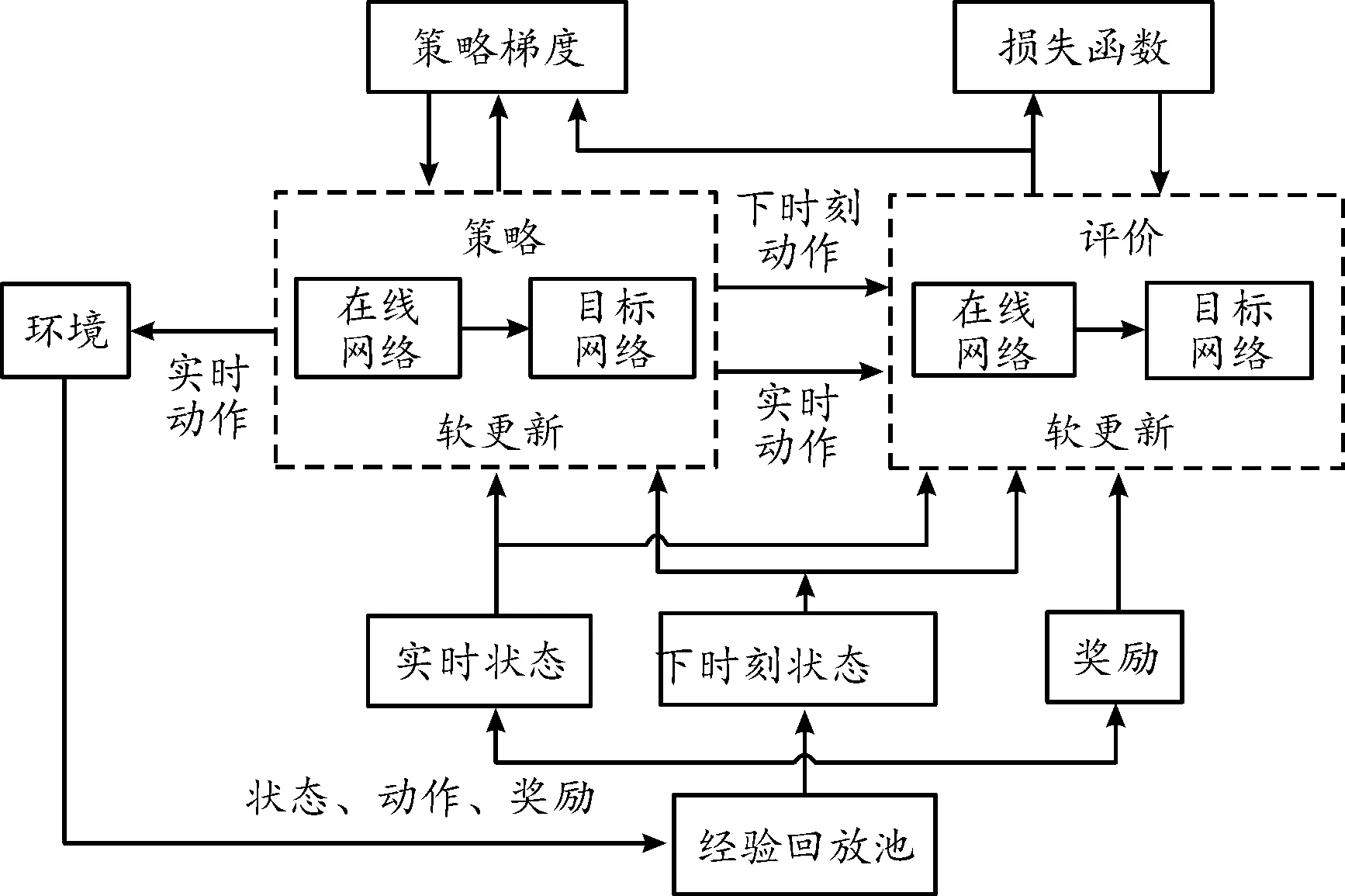
图3 DDPG算法结构框图Fig.3 DDPG structure
首先,为每艘无人艇设计策略网络和评价网络,其中的评价网络接收无人艇的状态和动作进行学习,策略网络只接收状态信息。该算法主要包括策略函数网络和评价函数网络,且每个网络均包括了主网络和目标网络,主网络和目标网络的结构完全一样,网络总体结构如图4所示。
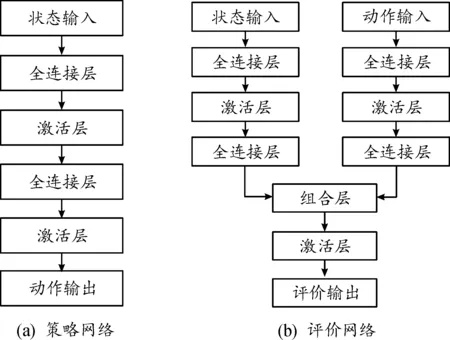
图4 策略网络和评价网络总体结构框图Fig.4 Network structure of actor and critic
DDPG算法是深度Q网络算法在连续动作空间的进阶版,因此DDPG同样存在目标值高估问题。针对该问题对算法结构做出如下改进:
1) 建立2套结构相同的评价网络,计算时序差分目标时采用2个目标网络输出中的较小值作为目标值,2个主网络均通过最小化均方差更新。
2) 降低策略网络的更新频率,促使评价网络更新更稳定。
3) 在目标策略网络的输出上增加一个服从正态分布的噪声,从而平滑值估计,避免评价网络过拟合。策略主网络更新时,采用2个评价主网络输出的较小值。
算法流程如下:
改进的DDPG算法
初始化策略网络和2套评价网络参数
初始化经验池
for episode=1,do
初始化智能体状态
for=1,do
为每一个智能体,选择加入噪声的随机过程动作
返回所有智能体的动作集合,奖励,下一个状态值
储存状态转移数据对到经验池
从经验池中随机选择最小批次数据
计算损失函数更新评价网络
计算策略梯度更新策略网络
“软更新”目标网络参数
End for
End for
其中,代表总回合数;代表回合时长。
奖励函数决定了深度强化学习的收敛速度与收敛程度,需要根据作业任务与环境来设置奖励函数。在传统强化学习中,奖励函数的设计通常做法是只有一个结果奖励,即只有在智能体到达最终目标时才会获得奖励,因此这种做法在操作规则较为复杂的任务中并不适用。为此,本文中将任务奖励分解为目标奖励与过程奖励两部分,通过赋予无人艇阶段性运动奖励来引导其学习到正确的围捕行为,得到最优博弈对抗策略的同时避免回报稀疏问题。针对协同围捕,下面设计红方无人艇奖励函数。
集体奖励函数为

(4)
式中:为第艘红方无人艇距蓝方无人艇的距离;为第艘红方无人艇与蓝方无人艇的角度。
=1+2+3
(5)
式中:1表示当红方与蓝方距离未达到包围范围时奖励,奖励考虑因素为平均距离;2表示当红方与蓝方距离达到包围范围时奖励,奖励考虑因素为相对角度;3表示规定时间内未完成围捕,红方任务失败。
4 仿真结果
为验证基于深度强化学习的无人艇集群博弈对抗策略有效性,下面分别进行5对1和7对3围捕下的集群博弈对抗仿真。
5对1下的仿真参数如表1所示。收益如图5所示,其中,回合收益表示一回合中每次迭代所获得的奖励的和,平均收益为最近一百回合收益的平均值。可以看出,收益整体呈上升趋势并最终稳定在较高水平,证明所建立的已经收敛。算法约在3 800回合收敛,最大奖励值为800,每艘无人艇均可到达目标位置完成围捕任务。

表1 5对1仿真参数Table 1 Simulation parameters under 5 vs 1

图5 5对1回合收益示意图Fig.5 Round reward under 5 vs 1
围捕仿真结果如图6所示,图6(a)为起始位置,图6(d)为围捕完成时位置,中间各时刻位置图相差14 s。在围捕初始时刻,红方无人艇位置相对分散,蓝方无人艇出现在红方无人艇北偏西方向。随后,红方向蓝方无人艇所在方向进行集中,逐渐接近蓝方无人艇;蓝方无人艇向目标区域靠近,并在红方无人艇接近时向北方向进行偏移躲避,状态如图6(b)所示。接着,红方无人艇追上蓝方无人艇并在其周围做伴随运动,逐渐形成围捕趋势;蓝方无人艇继续向目标区域靠近,状态如图6 (c)所示。最终,红方无人艇在蓝方无人艇到达目标区域前完成对蓝方无人艇的围捕,状态如图6(d)所示。

图6 5对1仿真结果示意图Fig.6 Simulation results under 5 vs 1
7对3下的仿真参数如表2所示。收益如图7所示,可以看出,收益值呈整体上升并最终稳定在较高水平,算法约在4 300回合收敛,最大奖励值为1 000,每艘无人艇均可到达目标位置完成围捕任务。
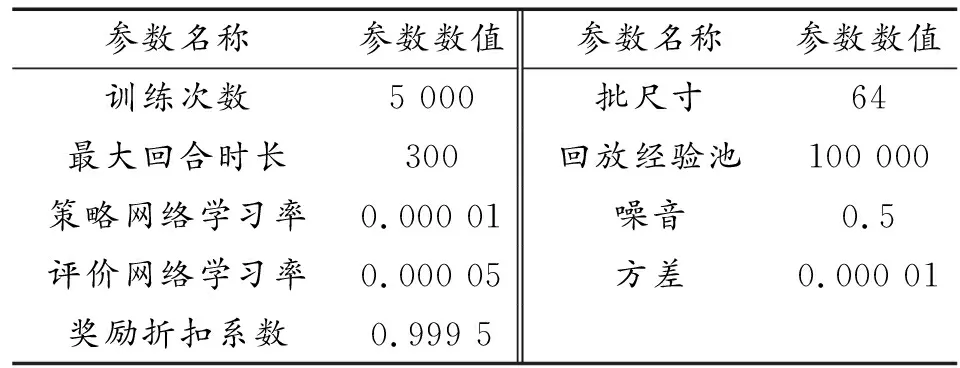
表2 7对3仿真参数Table 2 Simulation parameters under 7 vs 3

图7 7对3回合示意图Fig.7 Round reward under 7 vs 3
围捕仿真结果如图8所示,图中(a)为起始位置,(d)为围捕完成时位置,中间各时刻位置图相差32 s。在围捕初始时刻,红方无人艇与蓝方无人艇相距300 m左右,蓝方无人艇位于红方无人艇北方向,目标区域位于蓝方无人艇东北方向,红蓝双方位置均较为散乱。随后,红方无人艇向蓝方无人艇所在方向进行运动;蓝方无人艇边向目标区域靠近,边对红方无人艇追捕行为进行躲避,状态如图(b)所示。接着,红方无人艇追上蓝方无人艇,并在其周围逐渐展开围捕趋势;蓝方无人艇继续向目标区域运动,状态如图(c)所示。最终,红方无人艇完成对蓝方无人艇的围捕,围捕半径约为300 m,并以围捕状态伴随在蓝方无人艇周围进行运动,状态如图(d)所示。

图8 7对3仿真结果示意图Fig.8 Simulation results under 7 vs 3
5 结论
设计了协同围捕环境下深度强化学习算法的状态信息、动作信息、神经网络结构和奖励函数,并分别开展了5对1和7对3下的集群博弈对抗仿真验证。仿真结果表明,基于深度强化学习的红方无人艇集群能够对蓝方无人艇进行有效的协同围捕。未来工作将在此基础上研究弱连通下的无人艇集群博弈对抗。
