双重螺旋法加工螺旋锥齿轮齿面重合度设计

2022-10-14黄艳松李科锋

直升机技术 2022年3期

王豪，黄艳松，李科锋

(1.海军装备部，北京 100070； 2.中国航发湖南动力机械研究所，湖南株洲 412000)

0 引言

螺旋锥齿轮具有高承载能力、高传动平稳性、高重合度等优势，广泛应用于直升机传动系统、航空发动机等重载高速齿轮传动中。目前，螺旋锥齿轮加工方法主要为五刀法与双重螺旋法。相较于五刀法，双重螺旋法具有高效率、低成本、同批次齿轮几何精度一致性好、高速干切削等优点。由于螺旋锥齿轮齿面形貌较为复杂，在设计加工中质量控制较为困难，容易产生动态性能和振动噪声问题。经研究证明，工作载荷下的实际重合度和传动误差是影响振动噪声的主要因素。降低齿轮振动和改善接触性能，可采用增大齿轮副啮合重合度的方法。

目前提高重合度的方法主要为局部综合法：通过控制接触迹倾斜程度，大轮加工参数和小轮齿坯参数无需调整,仅对小轮加工参数进行设计,即可实现提高重合度的目的。但该方法主要针对五刀法，不适用于双重螺旋法。

本文针对双重螺旋法加工的螺旋锥齿轮，通过齿面主动设计的方法，控制齿面接触迹的倾斜程度以及传动误差曲线幅值，实现提高重合度，改善接触性能的目的。

1 重合度的基本概念

1.1 重合度定义

螺旋锥齿轮理论上为点接触齿面，在齿面为完全刚性的情况下，啮合迹线在齿面形成一条连续的点列，即为接触迹。在实际滚检和加载运行过程中，由于齿面的接触变形，在接触点周围形成瞬时接触椭圆，齿面的接触印痕由一系列的瞬时接触椭圆沿接触迹排列构成。齿轮在啮合过程中的重合度(Contact Ratio)定义为：

(1)

式中，为小轮单齿从开始进入啮合到退出啮合所转过的角度(时间)，=360°为小轮的啮合周期角度(时间)，为小轮齿数。

1.2 设计重合度与实际重合度

螺旋锥齿轮齿面具有准共轭特性，在传递载荷很小(趋于零)的情况下，实际重合度不受设计重合度影响，始终为1.0。此时齿面上的接触迹只有中间的一段参与啮合(图1中a- a′段)。当载荷增大，相应的齿面变形补偿了第二对齿间的间隙，潜在接触区发生齿面接触。参与啮合的接触迹长度增加，使得重合度增大,当齿轮副接触印痕达到齿顶时(图1中e点/ e′点)，重合度达到设计的最大值。当传递载荷继续增大，则会产生边缘接触，虽然重合度会略有增加，但过度的边缘接触容易造成振动噪音和强度破坏，应尽量避免。

1.3 接触迹与重合度的关系

接触迹的长度在一定程度上反映了齿轮的重合度，增长啮合过程中的接触迹能够提高重合度。当齿面接触迹与齿根夹角减小时，接触迹长度增加，增大，使得重合度增加。

1.4 传动误差曲线与重合度

在图1中，交叉点a和a′为轮齿传动过程中的啮合转换点，端点e和e′为齿面潜在接触迹的开始点和结束点，即实际重合度达到设计最大值，可得设计最大重合度可表示为：

(2)

式中，为小轮单齿从e点到e′点转过的角度(时间)。

图1 齿面接触分析示意图

2 重合度设计

根据齿面接触迹和传动误差曲线与重合度的关系，通过齿面主动设计的方法，在已有的大轮齿面方程的基础上，根据啮合关系获得与其完全共轭的基准齿面，确定所需接触迹和传动误差。在基准齿面的基础上获得小轮目标齿面，以小轮加工参数调整量为设计变量构建求解模型，求解获得期望重合度的齿面。

2.1 构建小轮基准齿面

如图2建立大轮和小轮之间啮合位置关系。其中，={;;;}为机床坐标系，固连于滚检机。={;;;}为大轮坐标系，随大轮转动，={;;;}为小轮坐标系，随小轮转动，和为辅助坐标系。在齿轮啮合过程中，小轮转角为，大轮转角为，为小轮相对于大轮的偏置距，为轴交角。

依据参考文献[4]，可得大轮齿面矢量方程(,)及其对应的法式()，分别转换到机床坐标系中，可得：

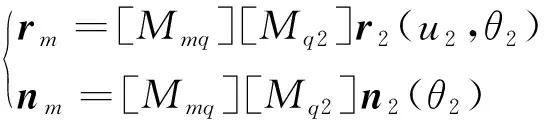
(3)

式中，

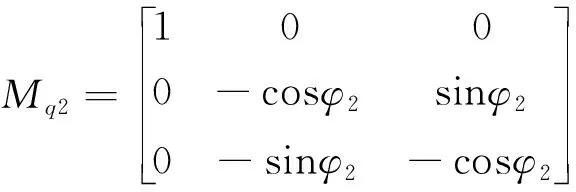
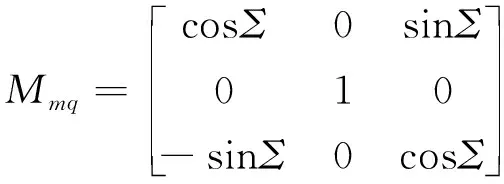
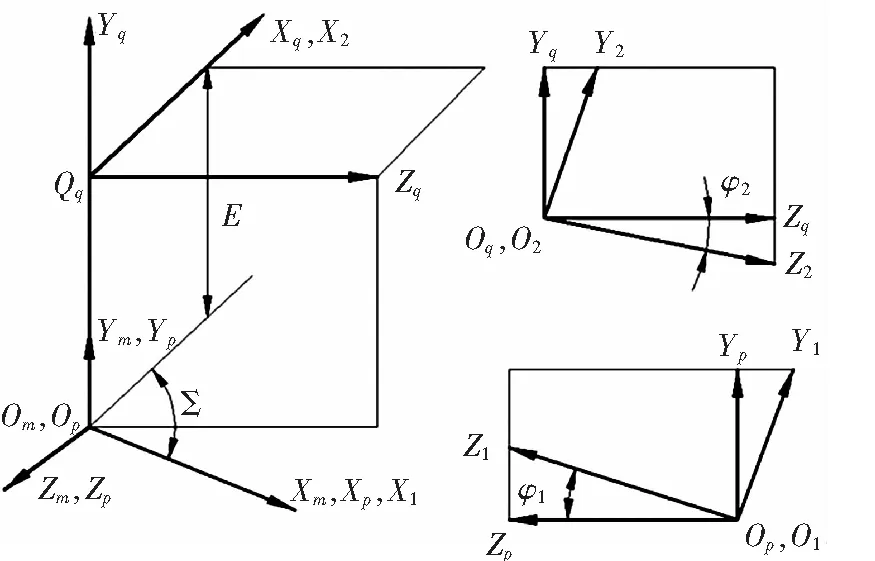
图2 啮合坐标系

大轮齿面与小轮齿面之间满足完全共轭关系，则有

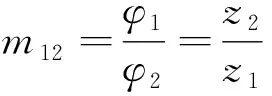
(4)

根据完全共轭啮合关系，可将大轮齿面方程转换至小轮坐标系下，从而获得满足完全共轭关系的小轮齿面如下：

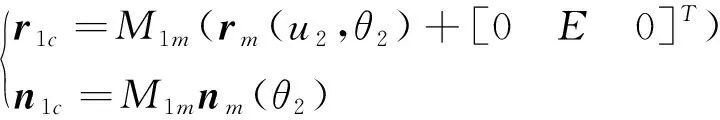
(5)

式中，

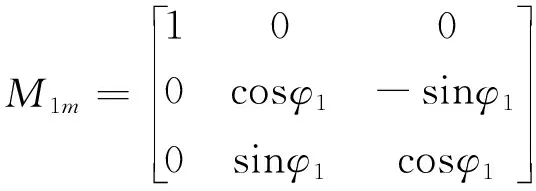
2.2 构建小轮目标齿面

在本文中，为了降低振动和冲击所带来的影响，将传动误差曲线设计为左右对称、开口向下的抛物线，传动误差可表示为：

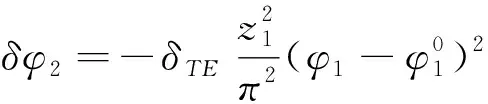
(6)

式中是啮合转换点处的传动误差幅值。

在齿面接触分析中，根据传动误差的定义可得实际传动误差曲线方程如下：

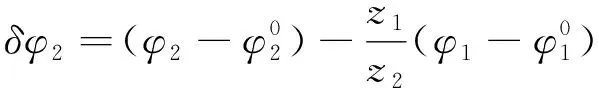
(7)

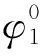
根据格里森技术标准，将齿面划分为5行9列共45点，并建立坐标系，如图3所示设置接触迹线。其方程可表示为：

(,)=-+(-)tan()=0

(8)

即在坐标系中，接触点迹线为一直线，其与方向夹角为，和为参考点坐标。

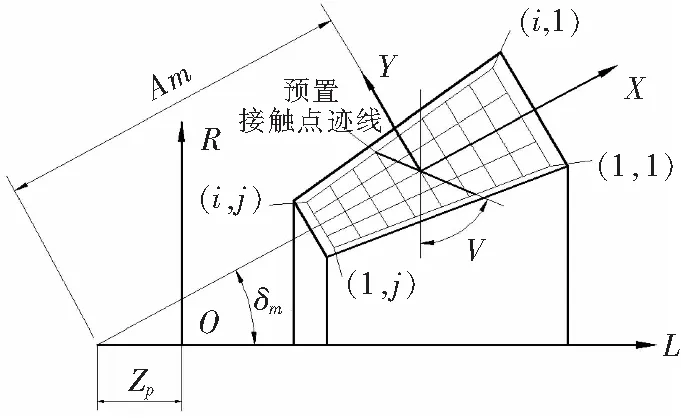
图3 齿面网格定义

为了能够使啮合过程中传动误差满足预置的条件，用式(6)和式(7)代替满足完全共轭关系时的运动关系式(4)，可得到满足公式(6)的新齿面，表达式如下：

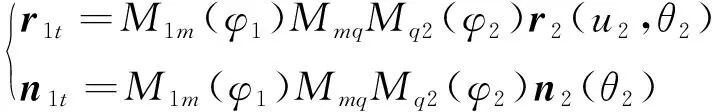
(9)

所得齿面大、小轮之间为线啮合，还需进行齿面修正，才能获得点接触齿面。取公式(9)齿面上的任意网格点，设置其沿法矢量方向上的齿面修正量为：

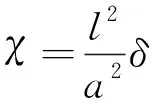
(10)

式中，为弹性变形量；为瞬时接触椭圆长半轴尺寸；为齿面任意网格点与预置接触迹线在切平面上的投影距离。

可得目标齿面上任意网格点的表达式为：

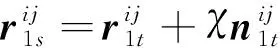
(11)

2.3 小轮加工参数求解

本文对小轮原齿面的加工参数进行调整以达到与目标齿面相逼近的目的。在实际加工中，刀具齿形角不易调整，故在此不予考虑。将小轮加工参数调整量Δ作为设计变量，小轮加工参数可表示为：

=+Δ

(12)

以求目标齿面和解获得齿面之间的偏差平方之和最小作为优化目标，上述齿面间在任意网格点上的法向偏差可表示为：

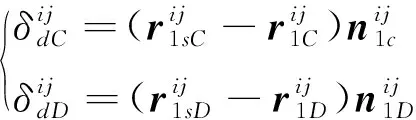
(13)

其中，角标和表示小轮凸面和凹面。将式(13) 中小轮原齿面加工参数用式(12)代替，即可获得优化的目标函数：

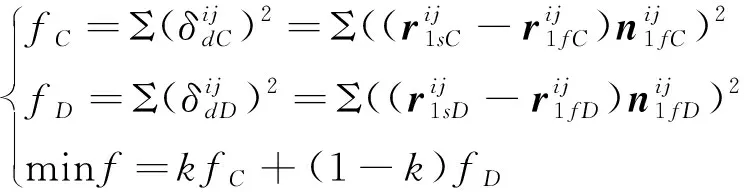
(14)

根据在实际应用中齿轮副两种转向的时长比确定加权系数。

本文采用MATLAB软件中的fmincon程序来对所建模型进行求解。对求解获得的齿轮加工参数通过MATLAB软件进行齿面接触分析，得到齿面接触印痕和传动误差曲线，进而检验齿面重合度情况；同时，根据大、小轮加工参数，通过齿面方程求解获得大轮和小轮的齿面三维坐标点，在三维软件完成模型构建后导入ABAQUS软件中开展有限元仿真，检验齿面接触性能情况。

3 算例分析

选取一对8×43准双曲线齿轮副作为原齿面，其为采用双重螺旋法加工。齿轮副基本参数和加齿参数如表1和表2所示。

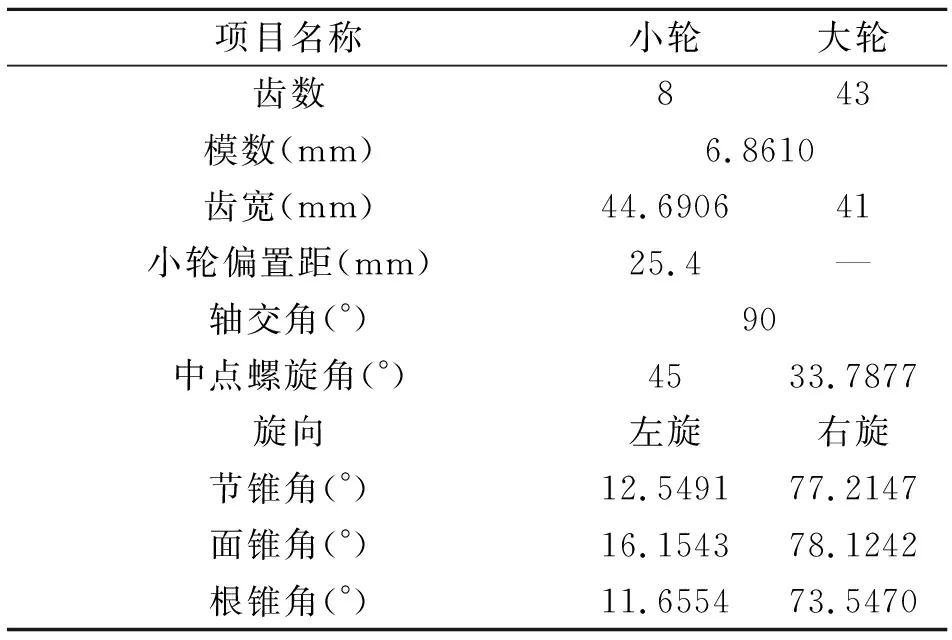
表1 齿轮副基本参数

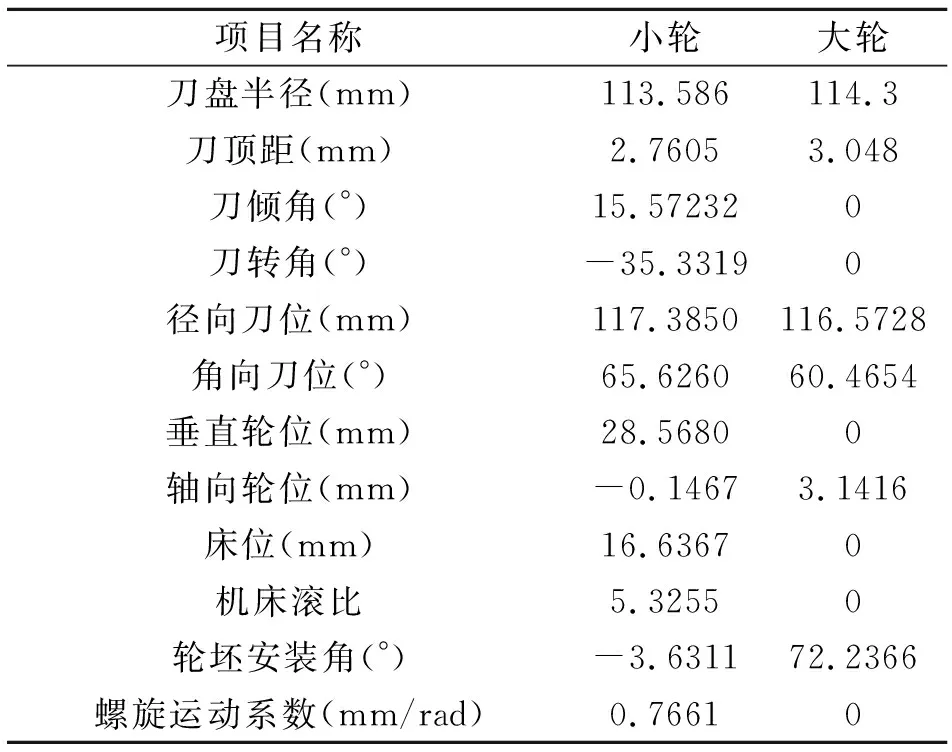
表2 齿轮副加工参数

传动误差曲线上的啮合转换点幅值反映了齿轮副对安装和加工误差的敏感性。本文针对低速重载的工况，改善齿轮副的啮合性能。满足该性能需加大齿面的接触迹倾斜程度，加大传动误差的啮合转换点幅值。如表3所示进行接触迹和传动误差曲线参数设置，其中实例一以原齿面为起始齿面，实例二以求解获得的实例一齿面为起始齿面，以小轮凹面为工作面，小轮凸面为非工作面。

表3 参数设置

为保证两侧齿面的啮合质量，对取值0.5，由式(14)的优化模型可获得实例一相应的小轮加工参数调整量，如表4所示；将实例一所得的小轮齿面作为实例二的起始齿面，求得的小轮加工参数调整量如表5所示。

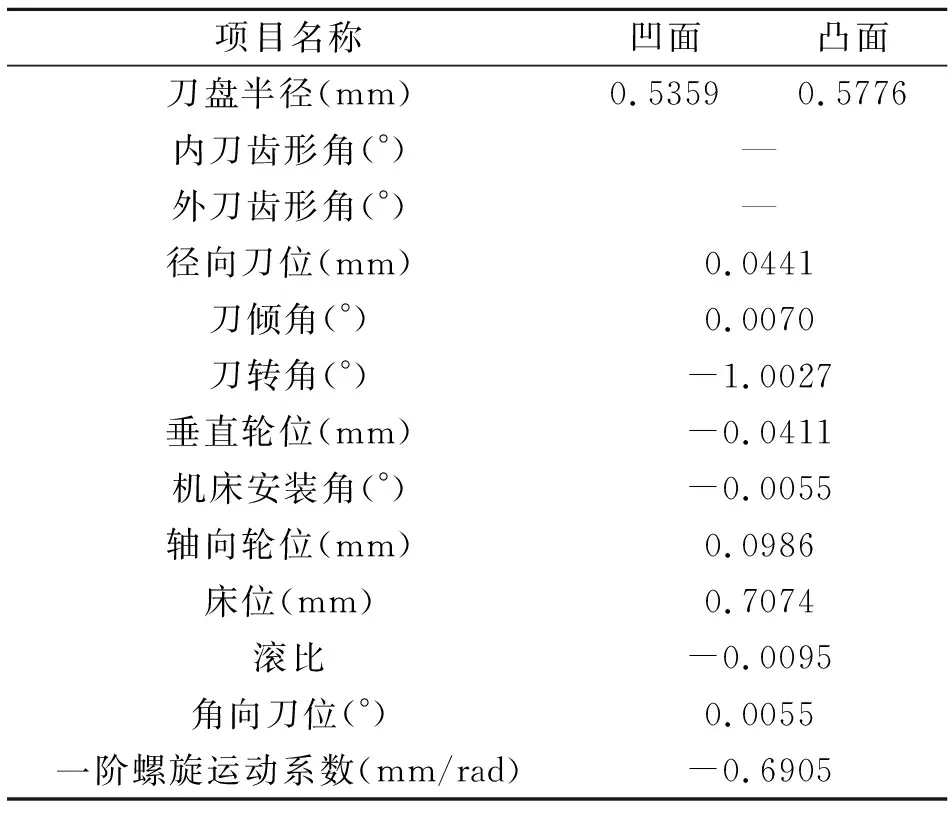
表4 实例一小轮加工参数调整量

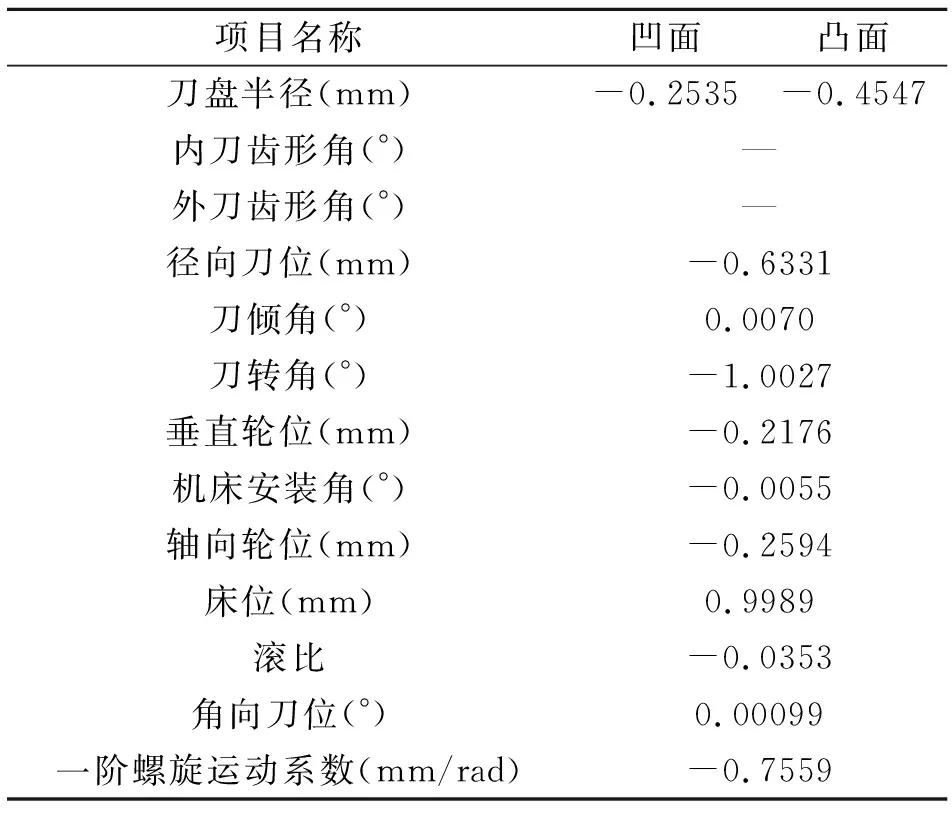
表5 实例二小轮加工参数调整量

对求解获得的齿轮副进行齿面接触分析，结果如图4和表6所示。

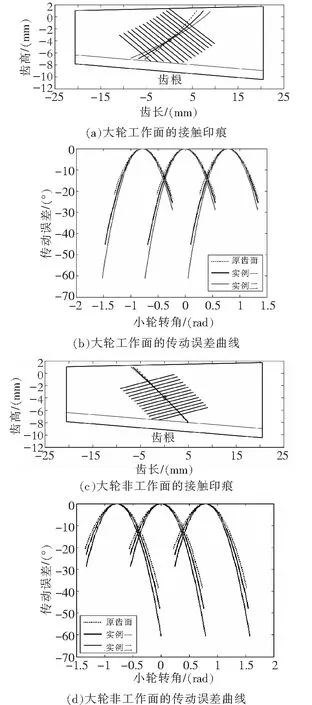
图4 齿面接触分析结果

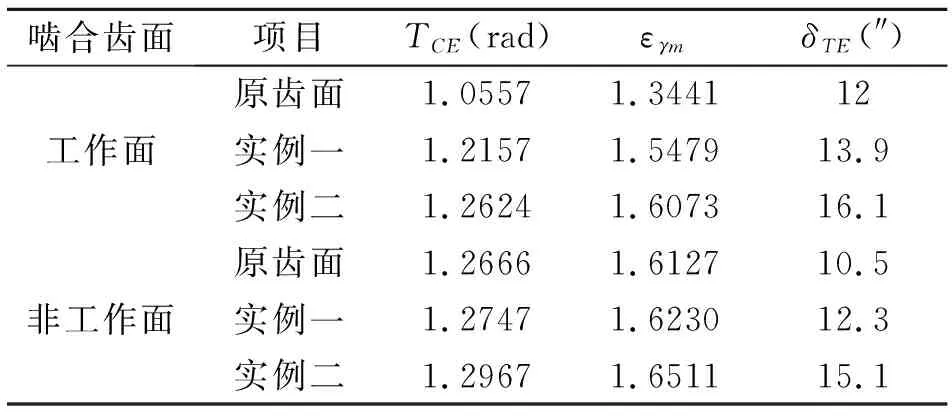
表6 结果参数

经分析可得：①原齿面、实例一齿面及实例二齿面之间，工作面和非工作面的接触迹线倾斜程度按设计逐渐加大；②原齿面、实例一齿面及实例二齿面之间，工作面和非工作面的设计最大重合度和啮合转换点处的传动误差幅值按设计逐渐加大。

图5为原齿面齿轮副、实例一齿轮副以及实例二齿轮副的工作面、非工作面在1000 N·m的负载下，齿轮副啮合过程中大轮齿面的接触压力情况。

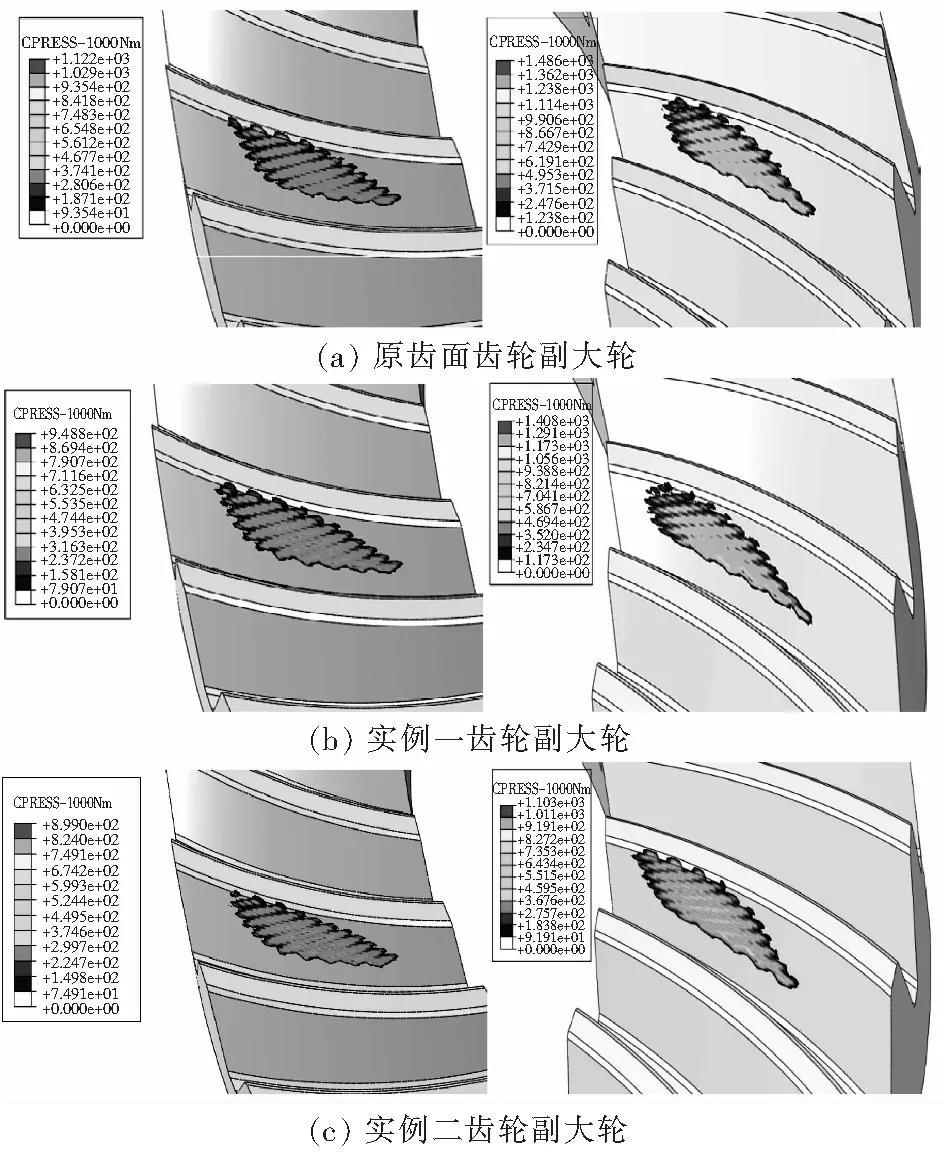
图5 1000 N·m下齿轮副接触压力情况

分析图5可得：①图中，工作面及非工作面均发生了边缘接触，潜在接触区参与了整个啮合过程，且边缘接触在大轮齿根部分较为明显；②在原齿面齿轮副中，接触压力较大区域主要集中在大轮齿根部分，在实例一齿轮副与实例二齿轮副中，接触压力较大区域有往齿面中部移动的趋势；③从图5中可得，原有实际齿轮副的最大接触压力最大，实例二齿轮副中的接触压力最小。

由此可得，针对低速重载工况下重合度设计的实例一和实例二达到了改善接触性能的效果，降低了最大接触压力，并对啮合传动过程中的边缘接触问题有所改善，达到了本文重合度设计的目的。