具有时滞的离散多智能体系统分组一致性研究

马洋洋，李伟勋，杜向阳，肖静宇

（天津职业技术师范大学理学院，天津 300222）

进入21世纪以来，伴随着人工智能与通信技术的快速发展，多智能体系统因在一些新型领域，如智能交通、传感器网络、无人机、计算机互联网、机器人等的潜在应用而受到控制领域学者的广泛关注与研究。一致性问题作为多智能体系统分布式协同控制中的基本问题，在各领域研究已较为成熟。为更好地满足工程实践的需求，数字控制系统的研究发展越来越深入，而离散系统理论作为数字控制系统的基本理论，也正在被越来越多的科研工作者所讨论研究。

研究者们对离散多智能体系统的一致性问题进行了深度研究，如Vicsek等[1]设计了一种具有动力学性质的粒子运动模型，并在较高群体密度且噪音较大的情况下，证明了所设计的动力模型可以使所有粒子的运动方向达到一致。Olfati-Saber等[2]系统地构建了多智能体系统的理论框架，并提出了离散时间一阶动力学系统模型。Tian等[3]在基于频域分析的基础上，通过结合应用Greshgorin圆盘定理得到了离散时间一阶多智能体系统在具有输入时延和通信时延的情况下，达到渐近一致的充分条件。对于二阶离散多智能体系统，Ren[4]基于有向固定拓扑结构下，对二阶离散多智能体系统进行了分析研究，证明了二阶线性多智能体系统在离散时间下，达到同步时可以趋于一个周期函数。Zhang等[5]证明了对于具有固定交换拓扑和随机交换拓扑的离散时间多智能体系统，当且仅当固定交换拓扑的图或交换拓扑的图存在有向生成树时，总存在缩放参数满足一致条件。Xie等[6]在文献[5]的基础上进一步解决了缩放标度参数的选择问题。

在具体的实际生活应用中，多个智能体的状态常常会分组趋于不相同的状态值。在文献[7]中Yu等首次在论文中探讨了在无向拓扑结构中一阶多智能体系统的组一致性问题。文献[8]和[9]研究了在有向固定拓扑结构下二阶多智能体的分组一致性问题，并且就离散时间情况下，固定拓扑结构的二阶多智能体分组一致性问题，提出了分组多智能体的一致性与选择控制参数和采样周期的关系。文献[10]研究了有向固定拓扑下二阶连续时间多智能体系统的2组一致跟踪问题，并将其结果推广到多组的情况中，也得到多组一致成立的条件。Huang等[11]在基于有向拓扑结构下，研究了具有间歇通信的二阶非线性多智能体系统的领导-跟随一致性问题，给出了多智能体系统实现一致性追踪的充分条件。以上文献研究的内容均有关多智能体系统能否达到一致性，并没有讨论多智能体系统的收敛速率，因此越来越多的研究者开始将指数一致性作为衡量系统收敛速度的重要指标。在文献[12]中讨论了连续时间多智能体系统的指数一致性问题，文献[13]进一步证明了连续时间多智能体系统领导-跟随指数一致性问题。Yang等[14]在系统是恒定耦合时延的情况下，研究了根据ADT信号进行切换的拓扑下神经网络的局部指数同步，但实际应用中具有较大的局限性。文献[15]利用2类时滞指数矩阵和迭代学习控制技术，研究了纯时滞二阶多智能体系统的一致性跟踪问题。Liang等[16]考虑了具有间歇通讯的时变时延一阶离散时间多智能体系统的领导-跟随指数一致性。实际上，在一些复杂的实际系统中，多智能体系统本身可能还会存在通信时间上的延迟。

通过对上述文献的分析，本文考虑了具有常时滞的二阶离散时间多智能体分组系统的领导-跟随指数一致性问题，设计了一种新的具有领导者的离散分组控制协议，利用李雅普诺夫稳定性理论和线性矩阵不等式方法，给出了在有向固定拓扑下保证离散时间二阶多智能体系统分组达到指数一致的充分条件。通过Matlab仿真实例验证所提出的控制协议的有效性。

1 问题描述与预备知识

1.1 图论知识

设图G={V，E，A}是一个有向加权图，V={v1，v2，…，vn+m，}是将n+m个智能体看作n+m个点后的集合，E⊆V×V是边的集合，其中，eij=（vi，vj）∈E表示智能体i能从智能体j处获取信息。在有向图里，如果节点vi到节点vj存在1条有向路径，则可以表示为（vi，vi1），（vi2，vi3），…，（vir，vj）。其中，vir∈V。如果在有向图中，只有1个节点能通向其他节点的有向路径，而并没有任何其他节点指向该节点的有向路径，那么此节点叫做根节点；如果除了根节点以外，其他所有节点有且仅有1个父节点，那么称此有向图为有向树；有向生成树就是由连接该图所有节点的有向边组成的有向树。如果1个有向图具有向生成树，那么其等价条件为存在1个节点具有能够通往其他所有节点的有向路径。A=[aij]∈R(n+m)×(n+m)是图G的邻接矩阵，其中aij为智能体i与智能体j之间的连接权重，当i=j时，aij=0。Ni={vj∈V:（vi，vj）∈E}为智能体i的邻居集。拓扑图G的拉普拉斯矩阵L=[lij](n+m)×(n+m)，其中，当i=j时当i≠j时，lij=-aij。和分别为点i的入度和出度是相应的度矩阵，则拉普拉斯矩阵满足L=D-A。

1.2 模型构建

在本文中，考虑n+m个跟随者和2个领导者构成的多智能体系统。首先将n+m+2个智能体分为2个子组，第1个子组G1为前n个跟随者（V1={v1，…，vn}）和1个领导者1，第2个子组G2为后m个跟随者（V2={vn+1，…，vn+m}）和1个领导者2，记S1={1，2，…，n}，S2={n+1，n+2，…，n+m}。令N1i={vj∈V1:（vi，vj）∈E}，N2i={vj∈V2:（vi，vj）∈E}，则Ni=N1i∪N2i。

考虑的二阶离散多智能体动力学系统描述如下，其中跟随者和领导者的动力学系统分别为

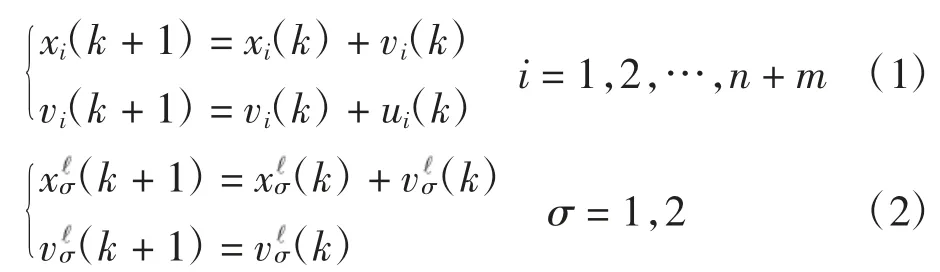
式中：xi∈Rn、vi∈Rn、ui∈Rn分别为第i个智能体的位置向量、速度向量和控制输入；∈Rn、∈Rn则分别为领导者的位置向量和速度向量。本文只考虑智能体在一维空间的情况，多维空间的情况可以通过使用克罗内积得到相应的结果。

受文献[10]中的控制协议的启发，并且基于领导者和跟随者的动力学系统设计了如下的控制协议

式中：增益系数α＞0，β＞0；∀i，j∈S1，aij≥0；∀i，j∈S2，aij≥0，∀（i，j）∈E0={（i，j）：i∈S1，j∈S2}∪{（i，j）：i∈S2，j∈S1}，aij∈R。

假设τ是一个整数时滞且满足τ＞0。如果智能体i可以从领导者处获得信息，则bi＞0，否则bi=0。

注1本文中2个领导者之间不存在任何的信息交流，且每个领导者只能与本组的跟随者之间传递信息。

注2在信息交流中只有跟随者之间的信息传递存在时滞，跟随者与领导者之间的信息交流不存在时滞。该协议使各个智能体能与领导者之间的信息互相交流，且比智能体间不具有时滞通信情况下的协议更具普遍性，更贴近现实生活中的情况。

为定理的证明，本文给出以下的假设与引理。

假设1本文所研究的有向拓扑图是包含有向生成树的连通拓扑图，并且生成树的根节点为领导者。

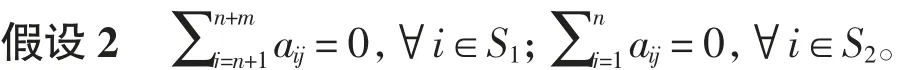
引理1[15]（Schur补）对于任意给定的矩阵

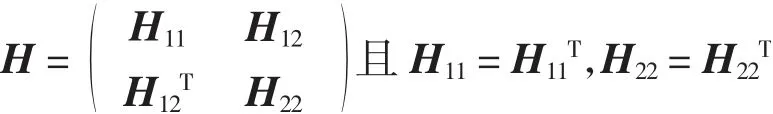
则有

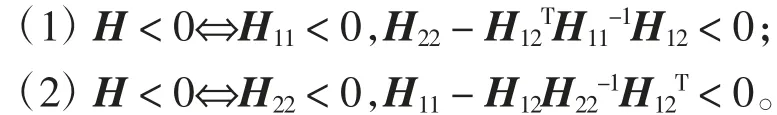
引理2[15]对于任意的实向量x∈Rn和y∈Rn正定矩阵P∈Rn×n，都有下列不等式成立

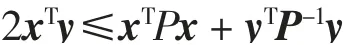
将领导者与跟随者之间的位置状态向量与速度状态向量分别做误差得到如下的误差系统。

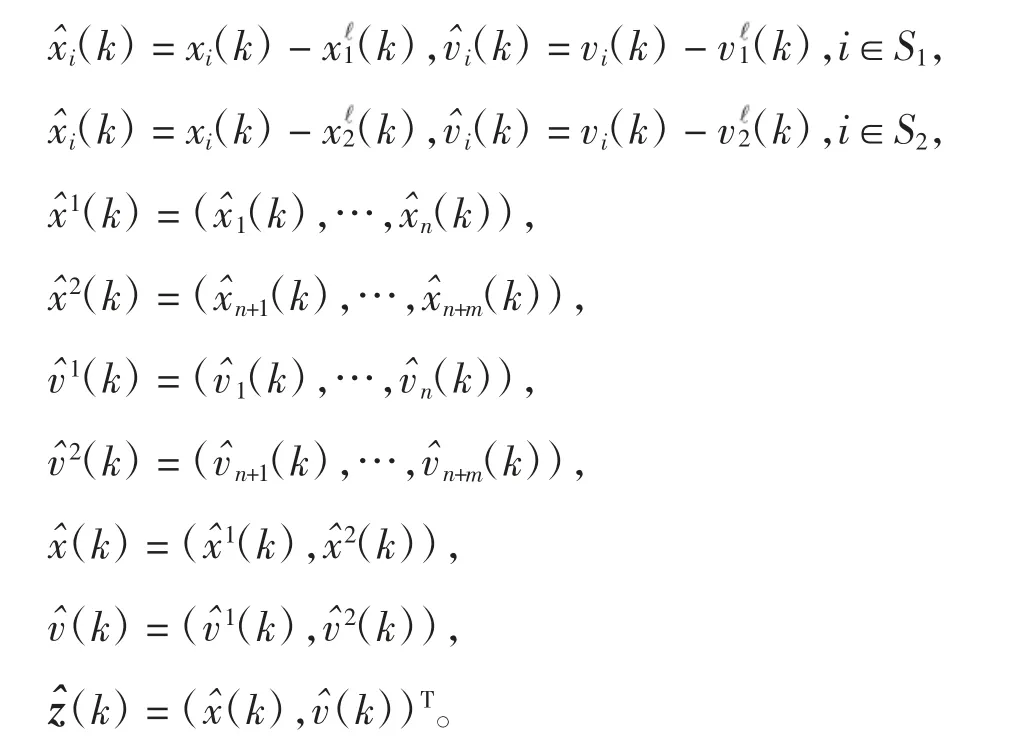
基于假设的条件下，根据控制协议（3）将系统（1）和（2）写成如下的误差矩阵形式

式中：L1、L2分别为第1组和第2组的跟随者拓扑图的拉普拉斯矩阵。

定义1[13]如果具有收敛速率θ的误差系统是指数稳定的，即存在标量θ＞0，ρ＞0，使得下式成立

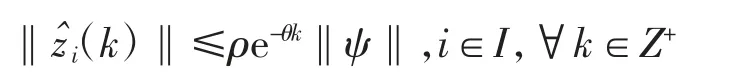
2 主要结果

利用矩阵论和稳定性分析来建立有向固定拓扑下离散多智能体实现分组一致的条件。以下的定理给出了系统实现分组一致性的充分条件。

定理1基于假设成立的情况中，对于给定的标量θ＞0，τ＞0，如果存在矩阵X1＞0，Y1＞0，满足下列式

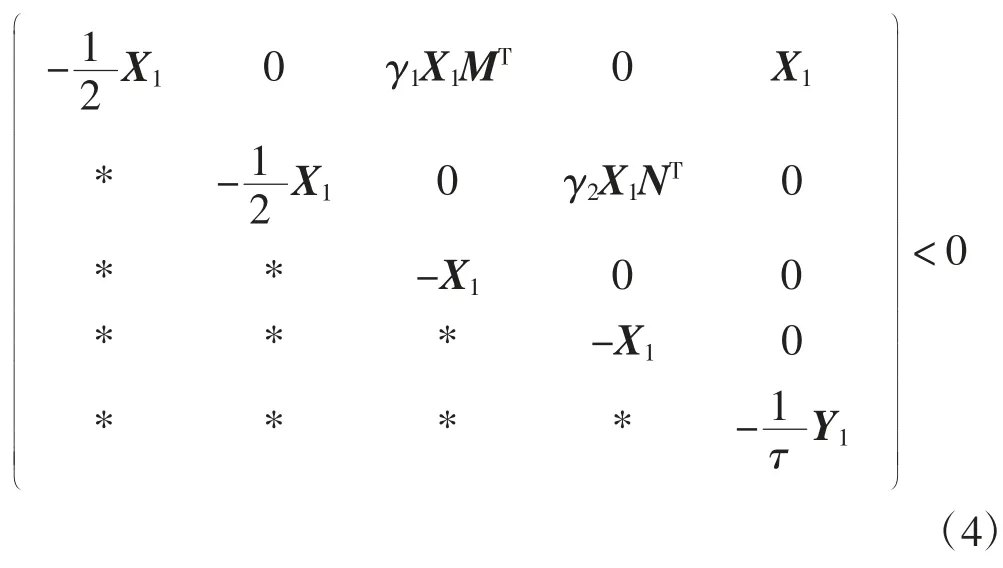
则在控制协议（3）下，具有常时滞的领导-跟随的二阶离散多智能体系统的分组指数一致性问题是可解的。

证明令（k）=eθk（k），θ＞0，则得到新的误差系统为

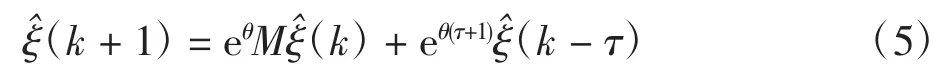
定义如下的Lyapunov-Krasovskii泛函

对V1（k）做差分得到

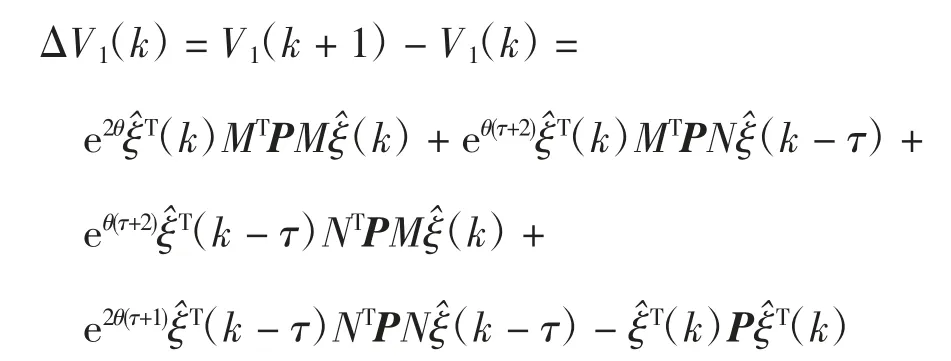
运用引理2可以得到

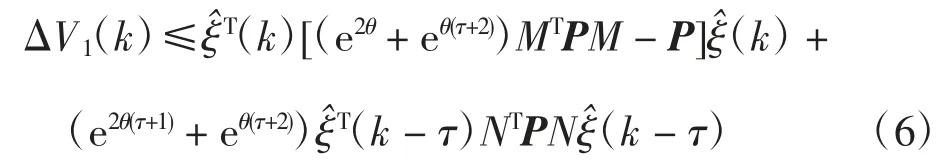
对V2（k）做差分得到

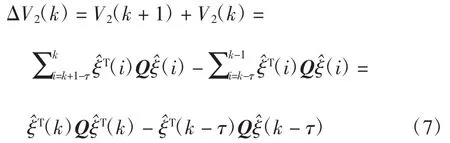
对V3（k）做差分得到

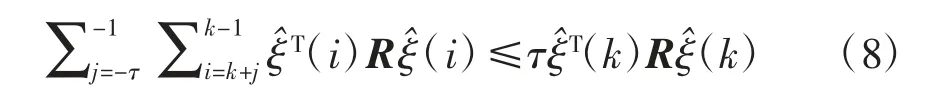
由式（5）至式（7）可以得到

运用引理1，可以得到Π＜0，当且仅当

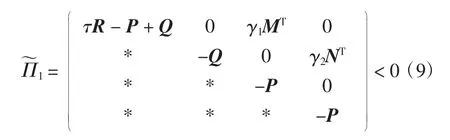
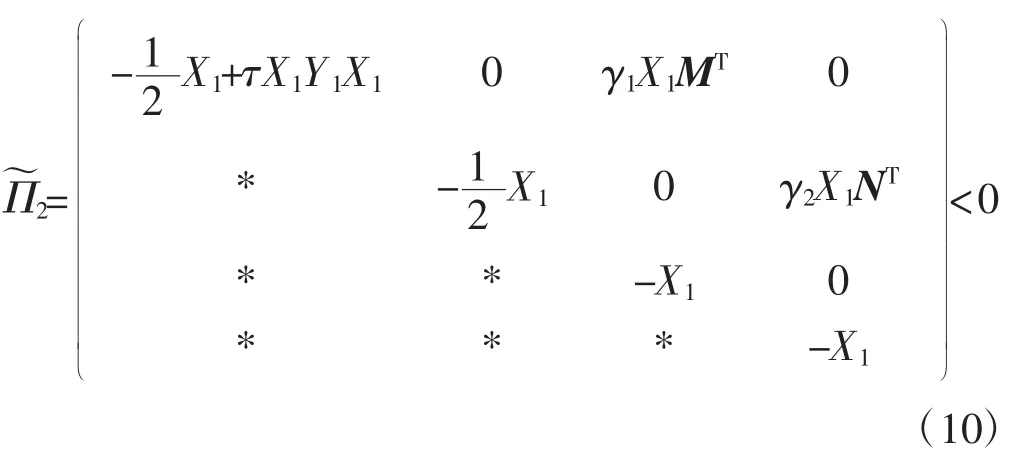
如果式（10）成立，根据引理1可知式（4）也成立，则Π＜0成立，因此ΔV（k）≤0，显然V（k）是递减的，可以得到

则

即

因此根据定义1，可以得到误差系统（5）是指数稳定的，所以本文中的具有常时滞的领导-跟随二阶离散多智能体系统可以达到分组指数一致性。

3 数值模拟

数值模拟采用一个Matlab数值仿真实例来说明所设计的离散分布式控制协议的合理性。

例1在满足以上提出的假设的条件下，给出智能体之间通讯交流的有向拓扑图1，并给出拓扑图中各个智能体的初始状态，初始位置为[-20；45；-35；250；-25；-50；-45]，初始速度为[1；7；5；2；35；4；8]，取α=0.115，β=0.45，τ=1，智能体间通讯拓扑图如图1所示，根据Matlab软件仿真后可以得到速度图、位置图、速度误差图、位置误差图，分别如图2至图5所示。

图1 智能体间通讯拓扑图

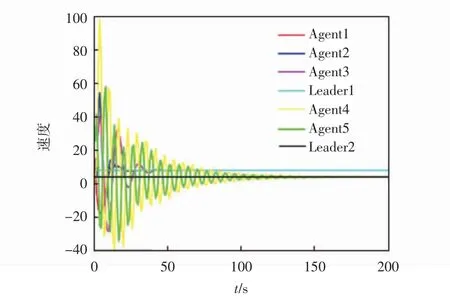
图2 速度图

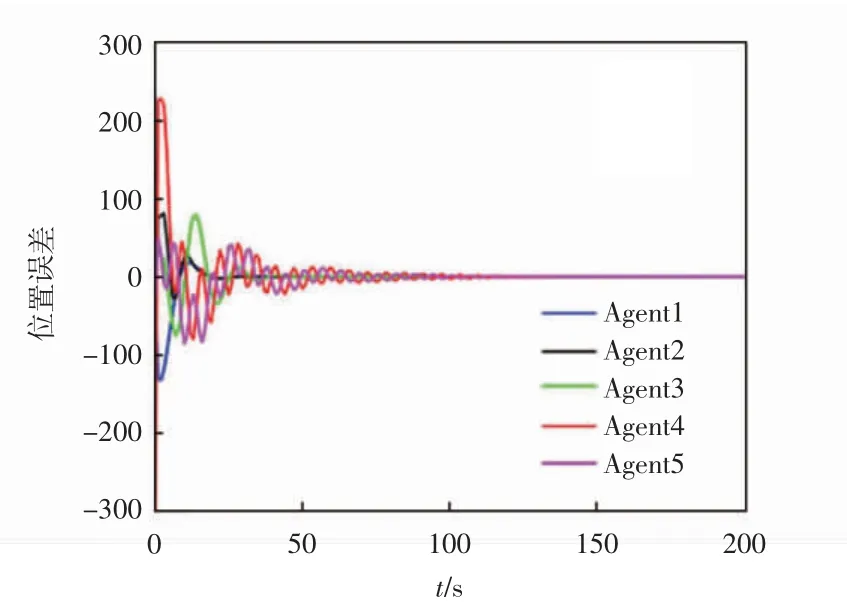
图5 位置误差图

从图2和图3中可以看出，每组智能体分别追踪上了其相对应的领导者；从图4和图5中得到各组智能体的速度误差和位置误差均可在200 s内逐渐收敛到0，故该仿真实验验证了本文所构建的控制协议的合理性。

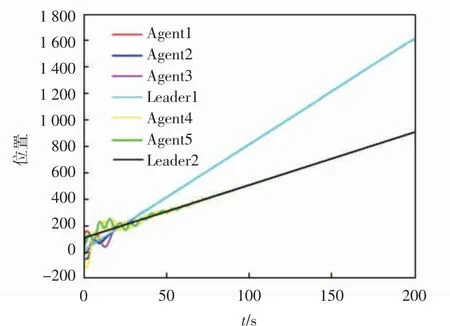
图3 位置图

图4 速度误差图

4 结语

本文研究了基于有向固定拓扑下的具有常时滞的二阶离散时间多智能体系统分组的领导-跟随指数一致性问题。针对二阶离散时间领导-跟随多智能体系统设计了一种新的分布式分组控制协议。通过使用矩阵分析工具，将领导-跟随指数一致性问题转化为系统的镇定性问题。基于李雅普诺夫函数和线性矩阵不等式方法，得到了二阶离散时间多智能体系统在有向固定拓扑下达到分组指数一致的充分条件，通过数值仿真验证了所设计的控制协议的合理性。