二次型价值函数的X-Y精密运动平台预测轮廓控制
2022-10-13王志强张秀云
王志强,张秀云
(1.天津职业技术师范大学汽车与交通学院,天津 300222;2.天津职业技术师范大学信息传感与智能控制重点实验室,天津 300222)
X-Y精密运动平台作为数控机床复杂加工工艺和高精密制造的基础,具有较大研究前景。各轴动态特性、运动惯性以及响应不及时等问题,极易引起高进给速度X-Y精密运动系统实际进给运动位置与理想曲线轮廓间产生较大误差[1-2]。
传统轮廓控制方法中单轴解耦轮廓控制可以看作是结合前馈和反馈的复合控制方法,文献[3-4]分别提出零相位误差跟踪控制方法和摩擦力补偿前馈控制方法,这2种方法的缺点在于对建模误差和非建模扰动2类干扰很敏感,而且未对多轴之间的协调运动进行考量。为实现轮廓误差的闭环控制,文献[5-6]分别提出变增益交叉耦合轮廓控制和迭代学习交叉耦合轮廓控制。然而,这2种方法的缺点在于不适用于其他更精确的轮廓误差估计方法,而且以上轮廓误差控制方案属于后补偿算法,存在固有的滞后性,在高速、高精度数控领域不易满足不断发展的加工需求。
相比传统轮廓控制方法,模型预测轮廓控制在多轴运动系统这种多输入多输出系统中更显现出明显的优势:不仅能够实现轮廓误差的直接预测控制,还能实现多目标优化控制[7]。借鉴预测控制思想,文献[8]提出模型预测轮廓误差预补偿策略,通过模型预测控制算法计算补偿信号,并添加到原始参考位置作为新的系统输入。文献[9]提出预测轮廓误差估计模型与在线迭代预补偿控制相结合的轮廓控制策略,通过在线迭代计算生成最优的轮廓误差补偿,以上方法均属于预补偿控制。文献[10]提出将内模原理和分层最优控制相结合的轮廓控制方法。文献[11-12]分别提出基于离散时间模型和线性时变模型的预测轮廓控制。文献[13]将预测轮廓控制应用于自动挖掘机系统的轨迹跟踪中,并将价值函数最小化为凸优化问题。文献[14]将广义预测控制应用于翼型系统跟踪设定轨迹中。文献[15]提出非线性预测轮廓控制在局部运动规划中的应用。文献[16]提出一种稳定化增量模型预测控制算法,设计具有可测扰动前馈-时滞状态反馈结构的模型预测控制器。文献[17]提出多轴运动系统有限控制集模型预测轮廓控制方法,将轮廓误差、跟踪误差、电机运行性能和电流幅值限制统一到一个价值函数中。以上方法的价值函数中都包含轮廓误差、跟踪误差等多个变量,必须考虑至少2个权重系数,而目前的整定方法仅局限于经验法或试凑法,存在依赖人工经验和耗时较长的问题。
为解决此问题,本文提出一种基于二次型价值函数的X-Y运动平台预测轮廓控制策略,建立X-Y运动平台的统一数学建模;设计基于二次型价值函数的FCS-MPC控制器,同时为了实现权重系数矩阵的自整定,采用基于Lyapunov稳定性分析的离线求解算法,并将得到的权重系数矩阵应用于有限控制集预测轮廓控制器的在线滚动优化过程,进行价值函数寻优。
1 X-Y运动平台数学建模
本文所选X-Y运动平台由表贴式PMSM驱动,运动机构、PMSM和两电平电压源逆变器数学模型参考文献[18],同时为实现X-Y运动平台统一建模,机械机构与PMSM关系为

式中:fi、ri、τi、pi、θi分别为驱动力、滚珠丝杠螺距、驱动转矩、滑块实际位置、转子机械角度。
因此,等效动态模型为

式中:Jeqi=Ji+Miri2/4π2;Beqi=Bi+Ciri2/4π2。
轮廓误差采用切线和圆形近似的方法,如图1所示。

图1 轮廓误差模型图
轮廓误差的计算公式[18]为

通过式(3)可近似求得轮廓误差的变化率为

速度期望值修正方法如图2所示。
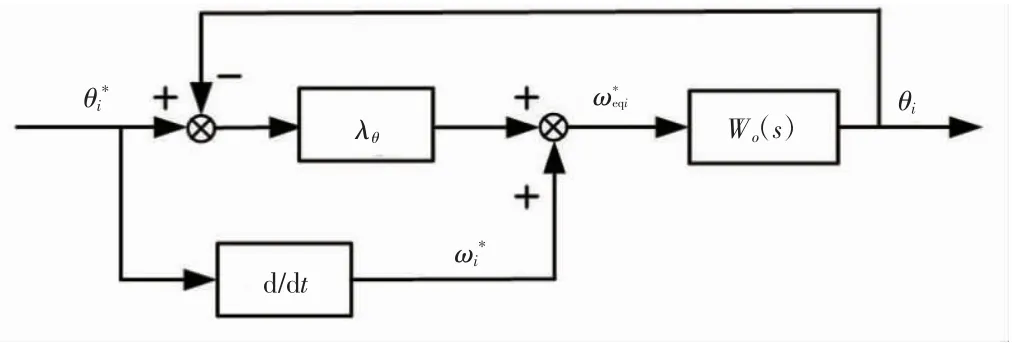
图2 速度期望值修正方法
速度期望修正值计算方法为

式中:λθ为比例系数;ωi*和pi*分别为速度和位置的参考值。
因此,预测模型可表示为
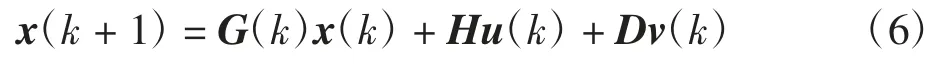
式中:x(k+1)=[ωx(k+1)ωy(k+1)idx(k+1)iqx(k+1)·idy(k+1)iqy(k+1)ε(k+1)]T;u(k)=[udx(k)uqx(k)·ud(yk)uq(yk)]T;v(k)=[TL(xk)TL(yk)ω*eq(xk)ω*eq(yk)]T;

Ai=1-TsmiBeqi/Jeqi;Bi=KtiTsmi/Jeqi;Ci=1-TsiRsi/Lsi;Di=-Tsipiωi(k);Ei=-Tsipiφfi/Lsi;Fi=TsmiriLi/2π;Mi=-Tsmi/Jeqi;Ni=Tsi/Lsi;本文中Tsi为电流采样周期;Tsmi为转速采样周期且Tsmi=10Tsi。
2 预测轮廓控制策略
2.1 价值函数的定义
现有方法通常定义价值函数为

价值函数包含4项:a为λεε2(k+1)—轮廓误差项,为了保证轮廓跟踪性能;b为λe(ω*eq(k+1)-ω(k+1))T(ω*eq(k+1)-ω(k+1))—跟踪误差项,为了保证速度的跟踪性能;c为λdidT(k+1)id(k+1)—id=0项,为了保证电流的跟踪性能;d为λq(iq*(k+1)-iq(k+1))T(iq*(k+1)-iq(k+1))—q轴电流跟踪误差项,以确保转矩的光滑性。
由式(7)可以看出,价值函数中需要同时整定4个权重系数λε、λe、λd、λq,整定过程依赖于人为主观经验,且随数量级的增大,整定次数会随之增加,算法的复杂度也会随之增加。但尽管如此,得到的也只是权重系数的大致取值范围,为解决此问题,本文重构二次型价值函数为
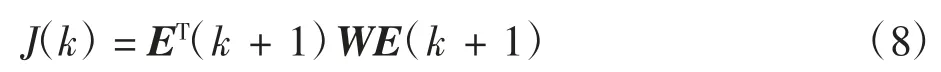
式中:权重系数矩阵W为7阶正定对称矩阵,E(k+1)=[ω*eqx-ω(xk+1)ω*eqy-ω(yk+1)idx*-id(xk+1)iqx*-iqx(k+1)idy*-idy(k+1)iqy*-iqy(k+1)ε(k+1)]T为7×1的误差矩阵,轮廓误差的参考值为0。
采用这样的重构方法,能够实现将权重系数的整定问题转换成求解J(k)中W的问题,根据现代控制理论中Lyapunov稳定性的知识,若W正定,那么就能够保证J(k)正定且单调递减,从而保证E趋于0。
2.2 二次型价值函数的求解
当系统进入稳态后,有x(k+1)=x(k)=x*,则稳态模型为
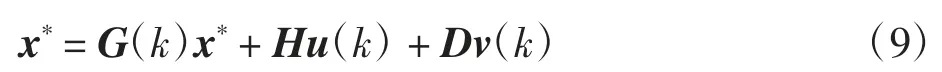
将式(9)减去式(6),可得

那么
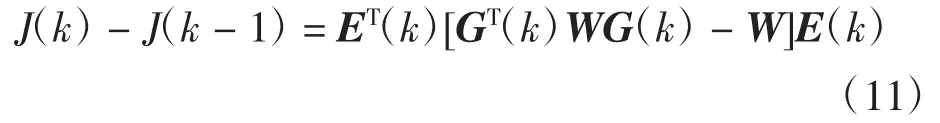
J(k)满足Lyapunov函数形式,且J(k)<J(k-1),即

将式(12)写为

将式(13)左右两边同时乘以V(=W-1),有
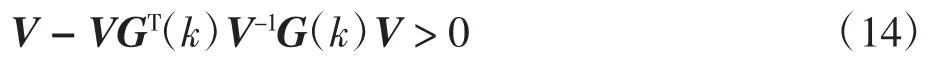
式(14)可等效为以下线性矩阵不等式(linear matrix inequality,LMI)形式
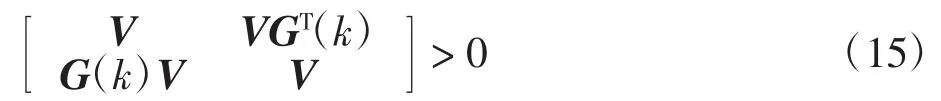
由于式(15)的解不是唯一的,因此需要定义一个最优解为

式中:f(V)为由V决定的函数,本文选取f(V)=SVST,S=[0 0 0 0 0 0 1],即满足轮廓误差在价值函数评估备选矢量过程中能够施加最大的影响。
同时,W还需要满足以下2个约束条件:
(1)由于相对电气动态性能来说,机械动态性能慢一个数量级,那么相对电流跟踪误差的权重系数来说,速度跟踪误差和轮廓误差的权重系数就需要一个较高的值,因此需增加一个约束条件,即
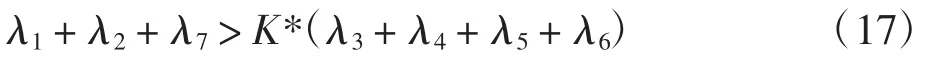
式中:λ1、λ2、λ3、λ4、λ5、λ6、λ7分别为E(k+1)权重系数矩阵中ωx*-ωx(k+1)、ωy*-ωy(k+1)、idx*-idx(k+1)、iqx*-iqx(k+1)、idy*-idy(k+1)、iqy*-iqy(k+1)、ε(k+1)项对应的权重系数;K为比例系数,通过试凑法获得。
(2)为实现轮廓误差在价值函数评估备选矢量过程中施加尽可能大的影响,相对于跟踪误差,轮廓误差的权重系数应尽可能大,因此需增加另一个约束条件,即

在双轴运动控制系统中,权重系数通过Matlab中LMI优化方法离线求得,然后再将其应用于算法的在线滚动优化过程。
2.3 稳定性分析
定理 考虑到离散时间系统(6)和恒定参考状态x*及其相对应的稳态控制输入u*满足式(9)。通过使用控制输入u(k)使式(8)的价值函数J(k)最小化,以保证随着k增大到无穷大,误差E(k)变为0,假设加权矩阵W是通过式(16)选择的[17]。
证明由式(11)至式(16)的论据可以证明,通过使用u能够保证J(k)<J(k-1),之后很容易得出通过使用最优的控制输入u(k),能够保证J(k)最小且J(k)<J(k-1),因此在每个时间步长使用最优控制输入即可得出
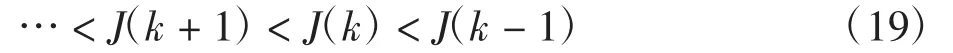
2.4 时间延迟补偿和备选矢量的确定
实际应用中,由于计算时间和调制机制会导致时间延迟,可能会降低性能,因此需要对此进行补偿。由式(6)可将预测矢量x(k+2)设为

价值函数修改为
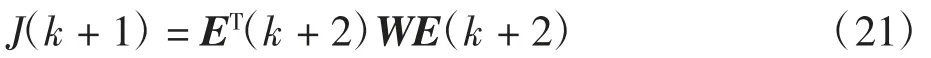
根据最小化价值函数J(k)的原则,从8×8个电压矢量中选取最优电压矢量Vopt作用于逆变器。
为降低在线计算量,应当减少单台逆变器的备选电压矢量个数,备选电压矢量选择方法参考文献[18],这样可将备选电压矢量个数降低为4×4,能够提高算法的实用性。
3 控制系统整体结构
现有提高轮廓加工精度的预测控制策略均需要进行权重系数整定,大多是采用经验法或试凑法,既增加了控制难度,又耗费了大量的时间在反复试验上。
针对此问题,本文结合模型预测轮廓控制在多轴运动系统这种多输入多输出系统中显现出的明显优势,设计统一的整体控制架构,同时控制两运动轴,然后为了实现权重系数矩阵的自整定,采用基于Lyapunov稳定性分析的离线求解算法,并将得到的权重系数矩阵应用于有限控制集预测轮廓控制器的在线滚动优化过程,进行价值函数寻优。同时,通过参考电压矢量位置角确定每扇区对应的备选电压矢量,增加扩展卡尔曼滤波(EKF)观测器避免角度测量中的量化噪声的影响[18],并增加电流限制模块(CL)[19]。X-Y运动平台预测轮廓控制结构框图如图3所示。
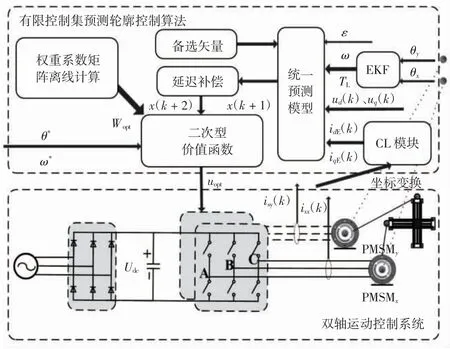
图3 X-Y运动平台预测轮廓控制结构框图
4 仿真研究
为验证所提出的X-Y运动平台预测轮廓控制策略的控制效果,通过Matlab软件进行Simulink仿真。当系统输入信号为折线运动轨迹时,并在0.1 s突加1 Nm负载,此时传统控制策略和所提基于二次型价值函数的预测轮廓控制策略下对应的动、稳态性能对比图如图4所示。
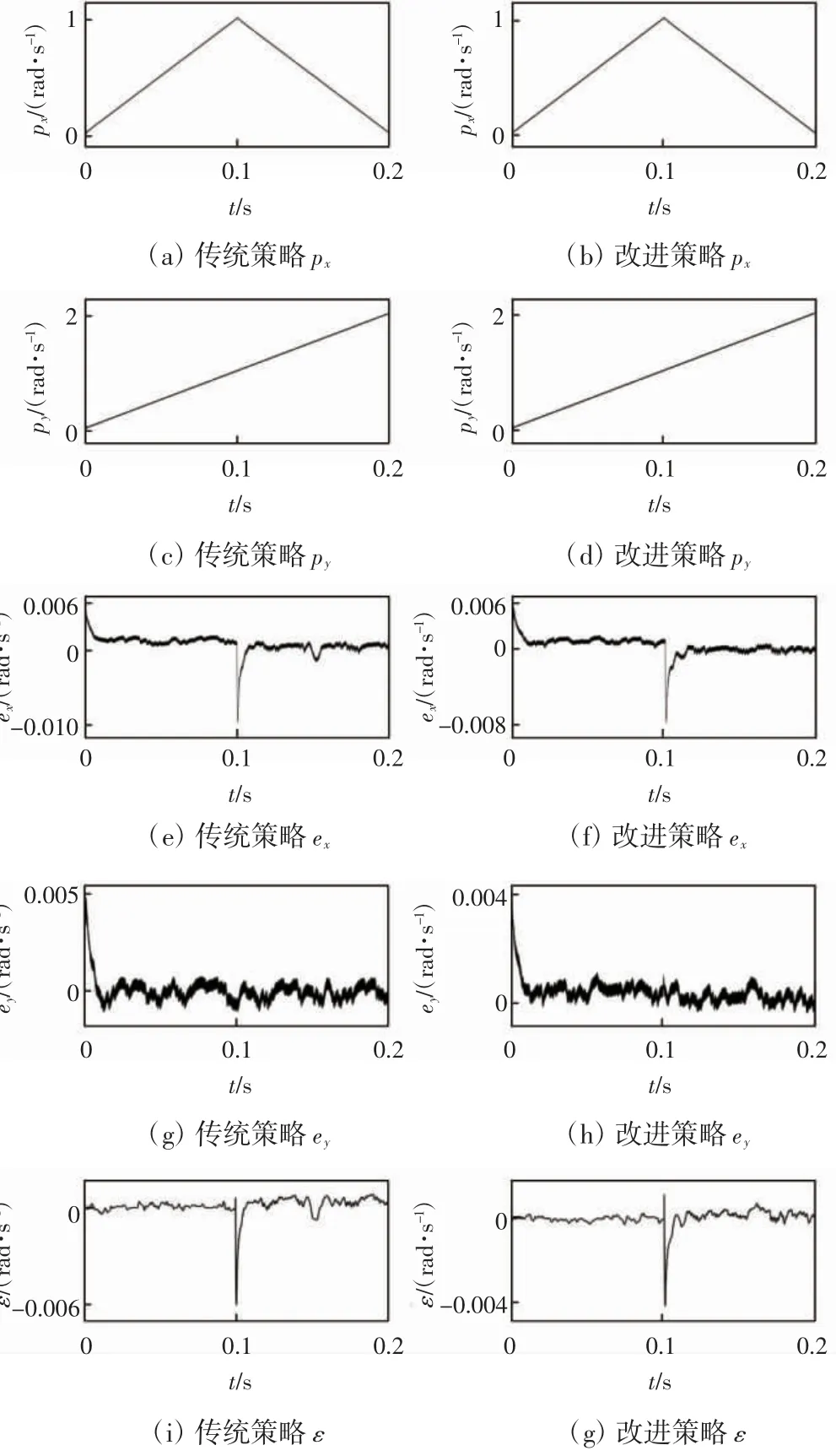
图4 跟踪折线轨迹时传统策略和改进策略下的动态性能和稳态性能对比波形图
从图4可以看出,采用2种控制策略时,稳态性能均能满足要求,而且针对轨迹转折点处的最大轮廓误差,改进策略比传统策略时要小。表1为采用传统控制策略和所提基于二次型价值函数的预测轮廓控制策略的综合对比。

表1 传统控制策略与改进控制策略的综合对比
由表1可知,改进控制策略下无需权重系数整定,且能够保证各误差项的收敛性,极大简化了算法复杂度。
当系统输入信号为圆弧运动轨迹时,并在0.1 s突加1 Nm负载。改进控制策略下,动、稳态性能图如图5所示。
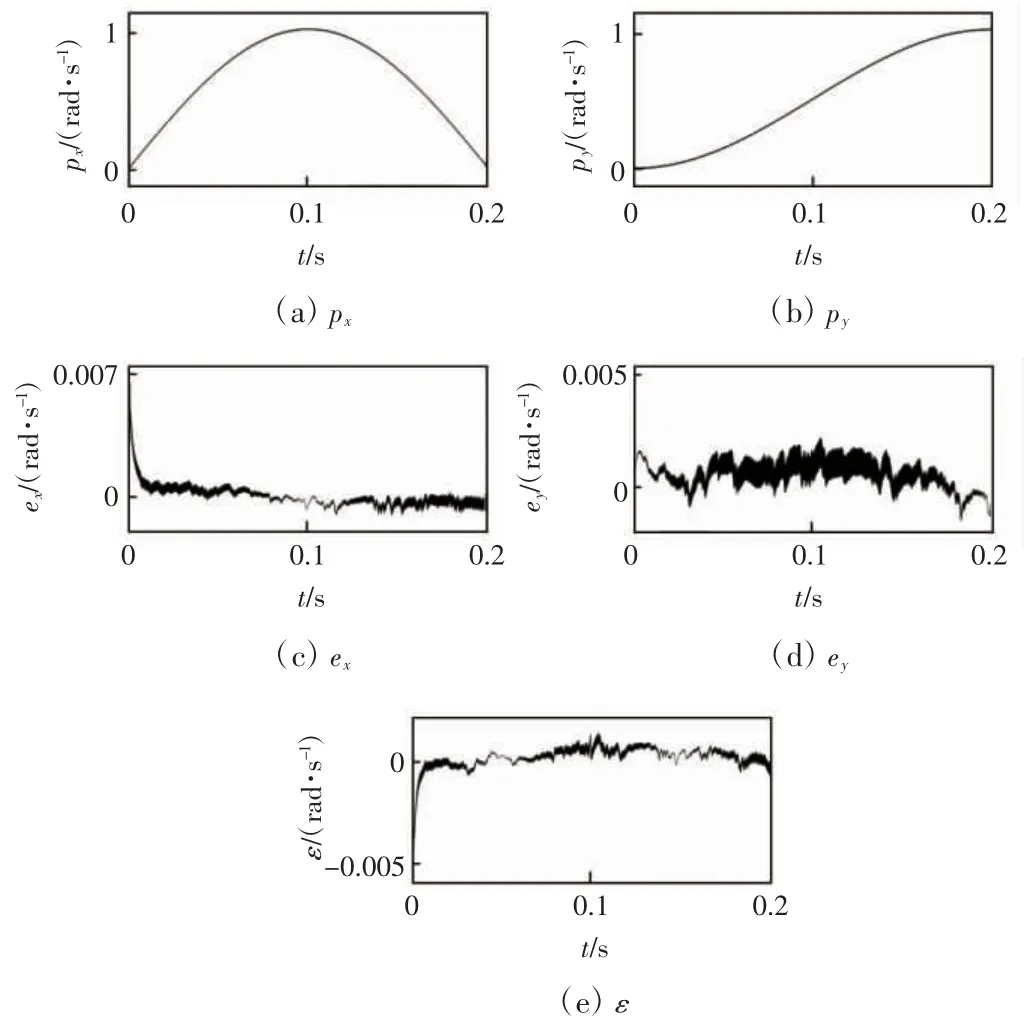
图5 跟踪圆弧轨迹时的波形图
从图5可以看出,x、y轴的跟踪效果较好,说明所提出的改进预测轮廓控制策略除了能够跟踪直线运动轨迹外,还能够跟踪圆弧运动轨迹。
5 结论
本文提出的改进控制策略具有以下优点:
(1)通过采用有限控制集模型预测控制,能够使系统轮廓跟踪精度得以提高。
(2)通过基于Lyapunov稳定性分析的离线求解算法,不仅能实现权重系数矩阵的自整定,保证各误差项的收敛性,而且能够减少权重系数整定所耗费的时间,避免依赖主观因素的影响,减小控制难度。
(3)通过设计二次型价值函数,用矩阵求解问题代替原来的多个权重系数整定问题,同时此方法易于拓展到多台电机的协同控制应用中。
