BDS-3卫星与其他GNSS系统卫星原子钟性能分析

伏军胜，贾小林，刘家龙，许 瑾，贺延伟，张 奋

（1.长安大学地质工程与测绘学院，西安 710054；2.西安测绘研究所，西安 710054）

0 引言

星载原子钟对卫星导航系统的性能起到决定性作用[1]。我国的北斗三号卫星导航系统（Beidou Global Navigation Satellite System，BDS-3）已于2020年7月31日正式宣布开通。研究分析BDS-3的原子钟性能，对于预测卫星导航系统的导航、定位和授时精度，推动星载原子钟发展是十分必要的。

国内外学者对星载原子钟的性能进行了大量研究，Zhao等[2]对BDS-3的卫星钟差特性进行了系统分析。张清华等[3]分析对比了北斗二号（Beidou Regional Navigation Satellite System，BDS-2）、全球定位系统（Global Positioning System，GPS）和格洛纳斯系统（Navigatsionnaya Sputnikovaya Sistema Global’naya，GLONASS）原子钟的性能，指出BDS-2在准确度和漂移率方面同GPS和GLONASS接近，但平均稳定性与GPS和GLONASS尚有一定的差距。目前对BDS-3星载原子钟的研究相对较少，尤其是针对北斗C37以后组网的卫星。本文利用一年的事后精密钟差数据研究BDS-3后期组网卫星原子钟的性能，并与其他GNSS卫星导航系统的原子钟性能进行分析比较。

1 星载原子钟性能评估基本原理

不同的卫星导航系统搭载着不同类型的原子钟，其中BDS-2全部为铷钟，BDS-3主要是铷钟，也有部分氢钟。GPS主要搭载的是铷钟，还有少量的铯钟。Galileo主要搭载的是氢钟，只有E11为铷钟。GLONASS搭载的都是铯钟，表1根据不同的轨道和卫星原子钟类型进行了分类统计。

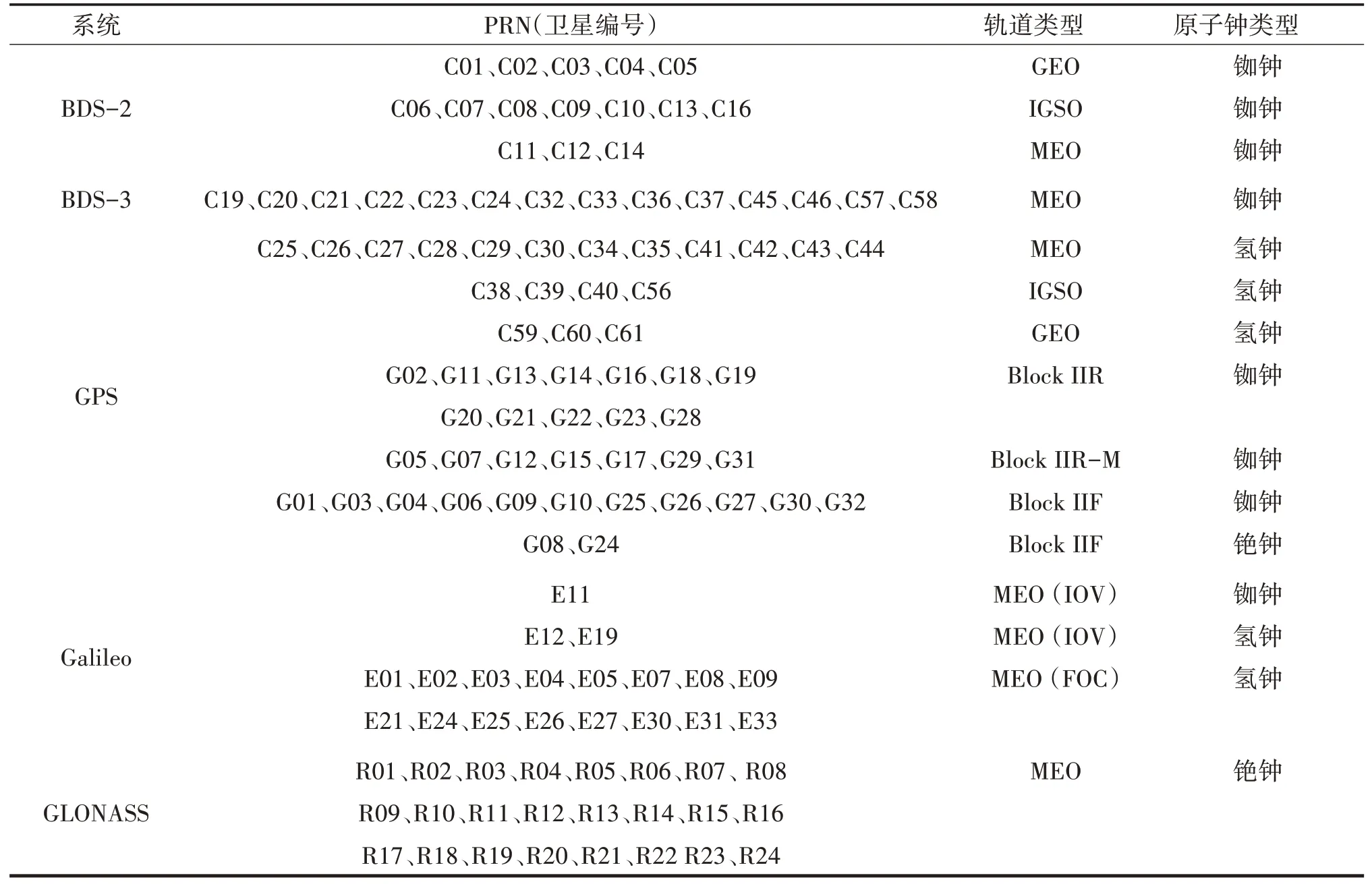
表1 GNSS卫星原子钟类型Tab.1 GNSS satellite atomic clock types

1.1 频率准确度

准确度表征的是真实值与理想值的关系，计算如下：

式中：σ为频率准确度；f1和f2分别为测量对象的实际频率和标称频率。

1.2 频率漂移率

频率漂移率又称频率老化率，是描述原子钟频率变化特征的参数。频率漂移通常是由于卫星运行过程中频标关键器件的老化和外界环境的影响造成的，频率值通常会随运行时间单调递增或递减。频率漂移率计算为：

1.3 频率稳定度

稳定度是表征振荡器在一定时间内产生同样时间和频率的能力，是表示给定时间内的频率偏差或时间偏差相对于平均频率偏差值或平均时间偏差值波动情况的统计特性。目前常用于稳定度计算的方差有标准方差、阿伦系列方差（Allan）和哈达玛系列方差（Hadamard）等[4]，目前评估卫星的稳定度采用最多的是哈达玛系列方差，是一种三次采样方差，适用于分析频漂比较明显的原子钟。由于阿伦系列方差不考虑线性漂移问题，而目前原子钟都有明显的频率漂移现象，所以选用哈达玛系列方差解决线性漂移问题。对于频率数据，哈达玛系列方差计算如式（3）。

对于相位数据，哈达玛方差计算如式（4）。

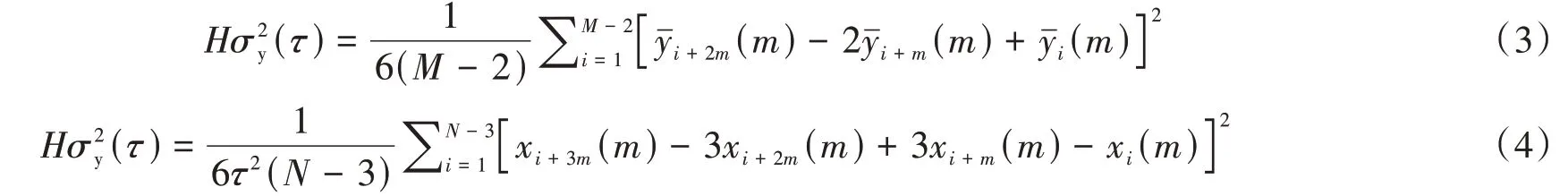
式中：Hσ2y(τ)为计算得到的哈达玛方差，τ=mτ0为平滑时间；τ0为采样间隔；M为平滑时间内̇i(m)的个数；m为采样数i(m)为第i个平滑时间内频率数据的平均值；N为平滑时间内相位数据总个数，N=M+1，xi(m)为第i个平滑时间内相位数据的值。

图1为星载原子钟性能评估的流程。

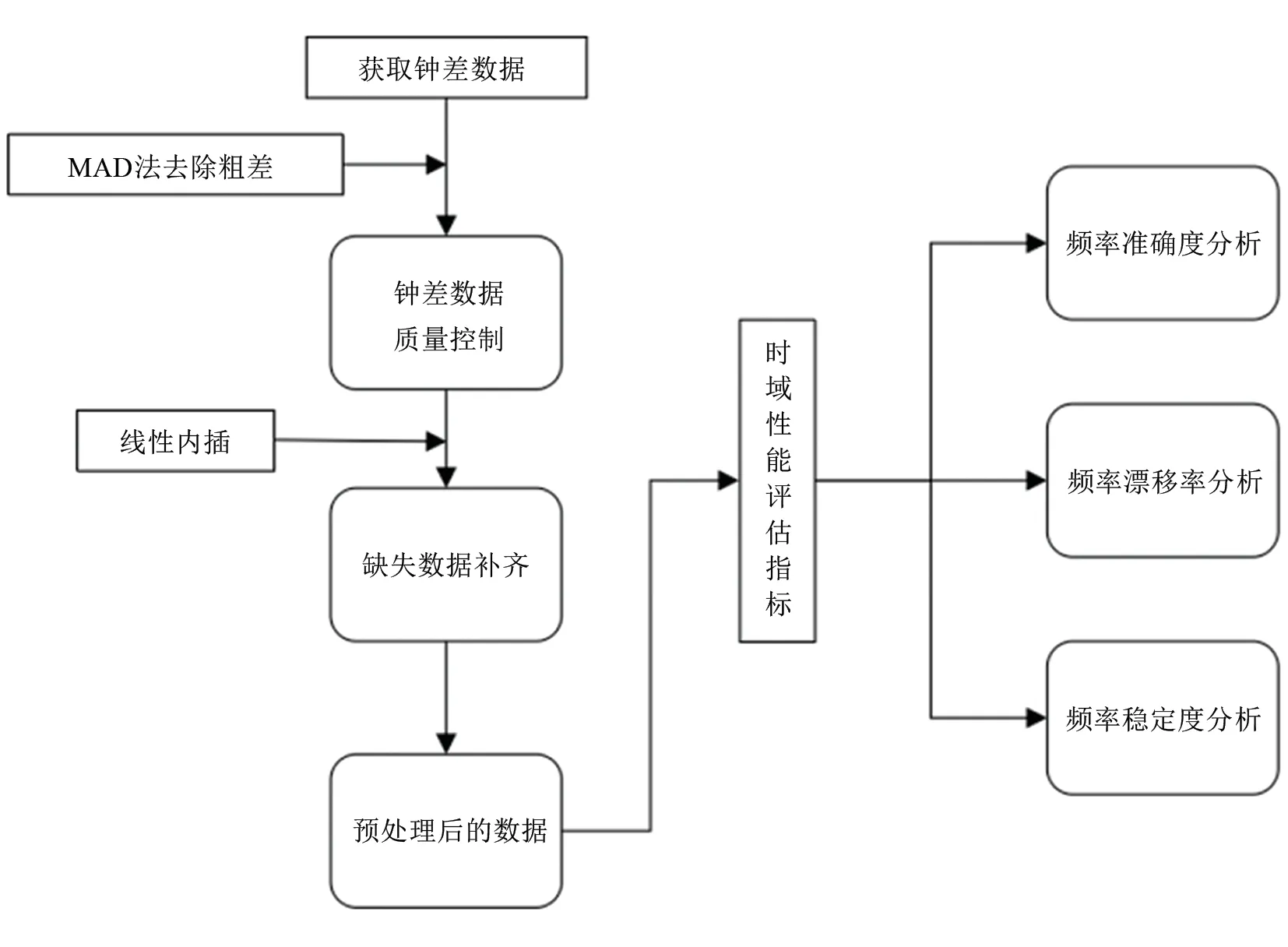
图1 星载原子钟性能评估流程图Fig.1 Analysis flow chart of spaceborne atomic clock

2 实验算例与分析

2.1 数据来源

实验采用德国地学研究中心（German Research Centre for Geosciences，GFZ）的事后精密钟差数据，数据日期为20200801-20210731。由于有数据缺失的情况，实验数据共363 d，采样间隔为30 s。

2.2 处理方法

卫星在轨期间受到外部环境的影响，钟差序列会产生粗差周跳等异常现象。为了消除基准钟不同产生的误差和参考基准跳变问题，可首先选取五颗性能表现较好的基准星对其钟差求取平均值，然后将各卫星的钟差与其作差得到的钟差数据进行计算。BDS-3选取了C26、C27、C28、C29和C30作为基准；GPS选取了G09、G10、G18、G25和G27为基准；GLONASS选取了R04、R11、R14、R15和R17为基准；Galileo选取了E04、E08、E12、E21和E24为基准。本文采用中位数法（Median Absolute Deviation，MAD）对粗差进行探测，该方法能够有效剔除钟差数据中的粗差。在数据处理时首先以天为单位对该天缺失的相位数据进行补全，使用线性内插的方法获得补全后的数据，统计缺失的天数并做标记，对数据进行分段。对于个别天没有对应的钟差文件或该颗卫星某一天钟差数据较差被整天剔除时，自动删除这些数据。粗差剔除时采用分段处理策略，当数值大于5倍中位数时进行剔除，对每段数据进行性能评估，包括频率准确度、频率漂移率和频率稳定度。其中稳定度包括千秒稳、万秒稳和天稳。得到各段结果后，对其取绝对值后求平均值进行分析，因此在结果中准确度和漂移率均是正数。

2.3 准确度分析

准确度是描述测量值与理想值符合程度的物理量。对一年的事后精密钟差数据，以月为单位对每颗星的准确度取平均值来进行分析。图2为GNSS原子钟的频率准确度变化情况。目前BDS-3处于2.62×10-13~4.77×10-11范围内，准确度均值随着月份的增加而有所提高；其中MEO卫星的氢原子钟的准确度均值为8.22×10-12，IGSO卫星的准确度为2.81×10-12，GEO卫星的准确度为4.18×10-12，MEO卫星铷原子钟的准确度为1.14×10-11；三种轨道类型中IGSO卫星氢原子钟的准确度最高，MEO铷原子钟的准确度最低。GPS多数卫星准确度位于10-12量级，G17和G24在后期的准确度数值较大；其中铷原子钟的准确度均值为5.21×10-12，铯原子钟的准确度均值为4.31×10-12。Galileo氢原子钟准确度均值为9.54×10-12；只有E11为铷原子钟，E11的准确度均值较氢原子钟高出两个数量级。GLONASS系统均为铯钟，准确度均值为1.29×10-12。通过准确度分析，BDS-3氢原子钟的准确度好于铷原子钟，使用氢原子钟的IGSO卫星准确度最高，优于MEO和GEO卫星。

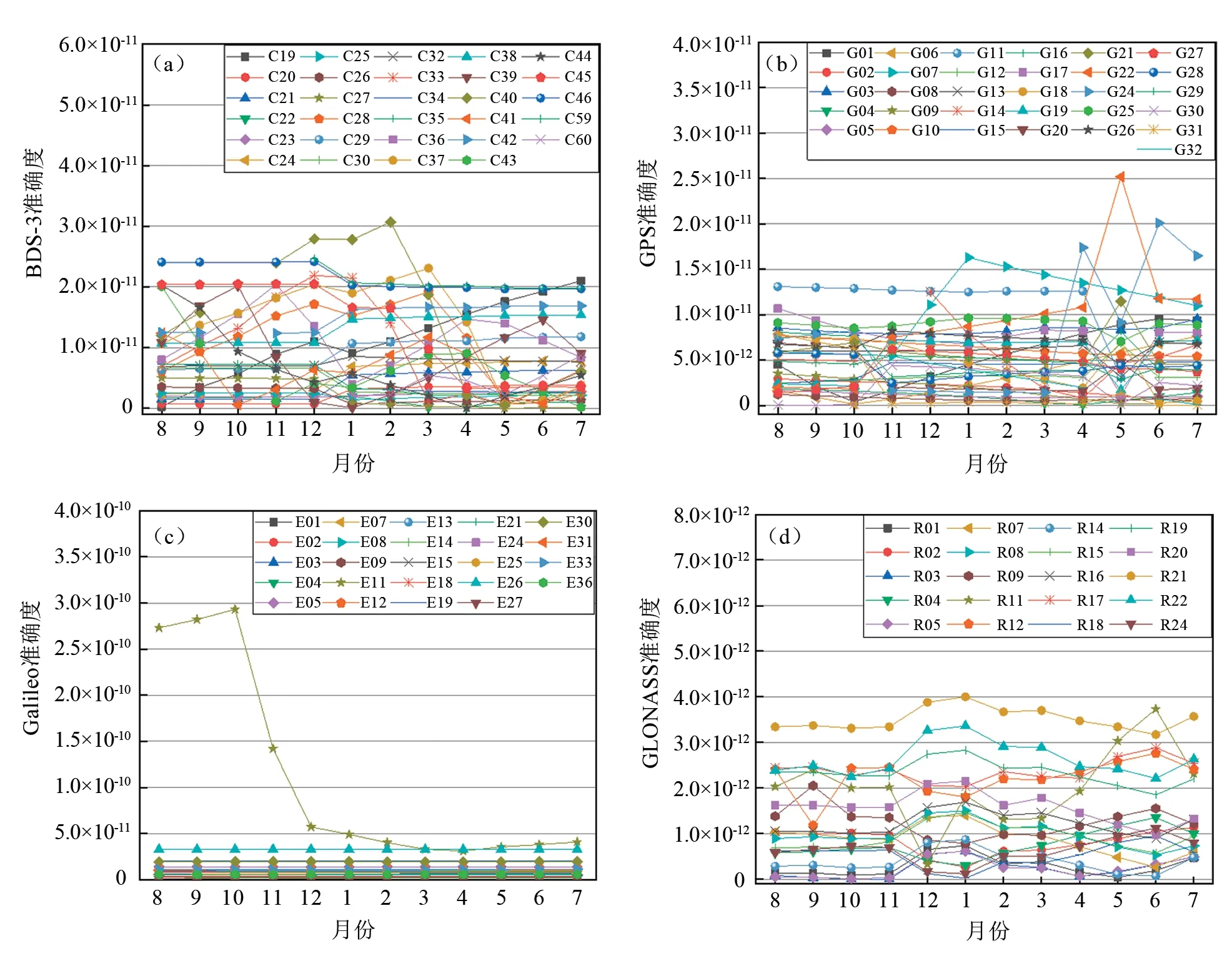
图2 GNSS星载原子钟频率准确度Fig.2 Accuracy of GNSS on-board atomic clocks

2.4 漂移率分析

频率漂移率反映的是原子钟的老化速度，是描述原子钟频率变化特征的参数。图3为GNSS原子钟的频率漂移率。目前BDS-3里MEO卫星铷原子钟的漂移率为7.67×10-15/d，氢原子钟的漂移率为5.31×10-16/d，铷原子钟的漂移率明显大于氢原子钟；IGSO卫星氢原子钟的漂移率为4.63×10-16/d，GEO卫星氢原子钟的漂移率为9.99×10-16/d。GPS漂移率位于2.26×10-16/d~8.68×10-15/d范围内，其中G14、G22和G24的漂移率较大；铷原子钟的漂移率均值为1.53×10-15/d，铯原子钟的漂移率1.21×10-15/d。Galileo卫星氢原子钟漂移率均值为1.29×10-16/d，E11铷原子钟的漂移率为2.05×10-14/d，高于其他卫星2个量级。GLONASS卫星的平均漂移率为7.63×10-16/d。由上述数据可知BDS-3氢原子钟的漂移率更好，比铷原子钟更加稳定，IGSO卫星氢原子钟的漂移率优于MEO卫星和GEO卫星。

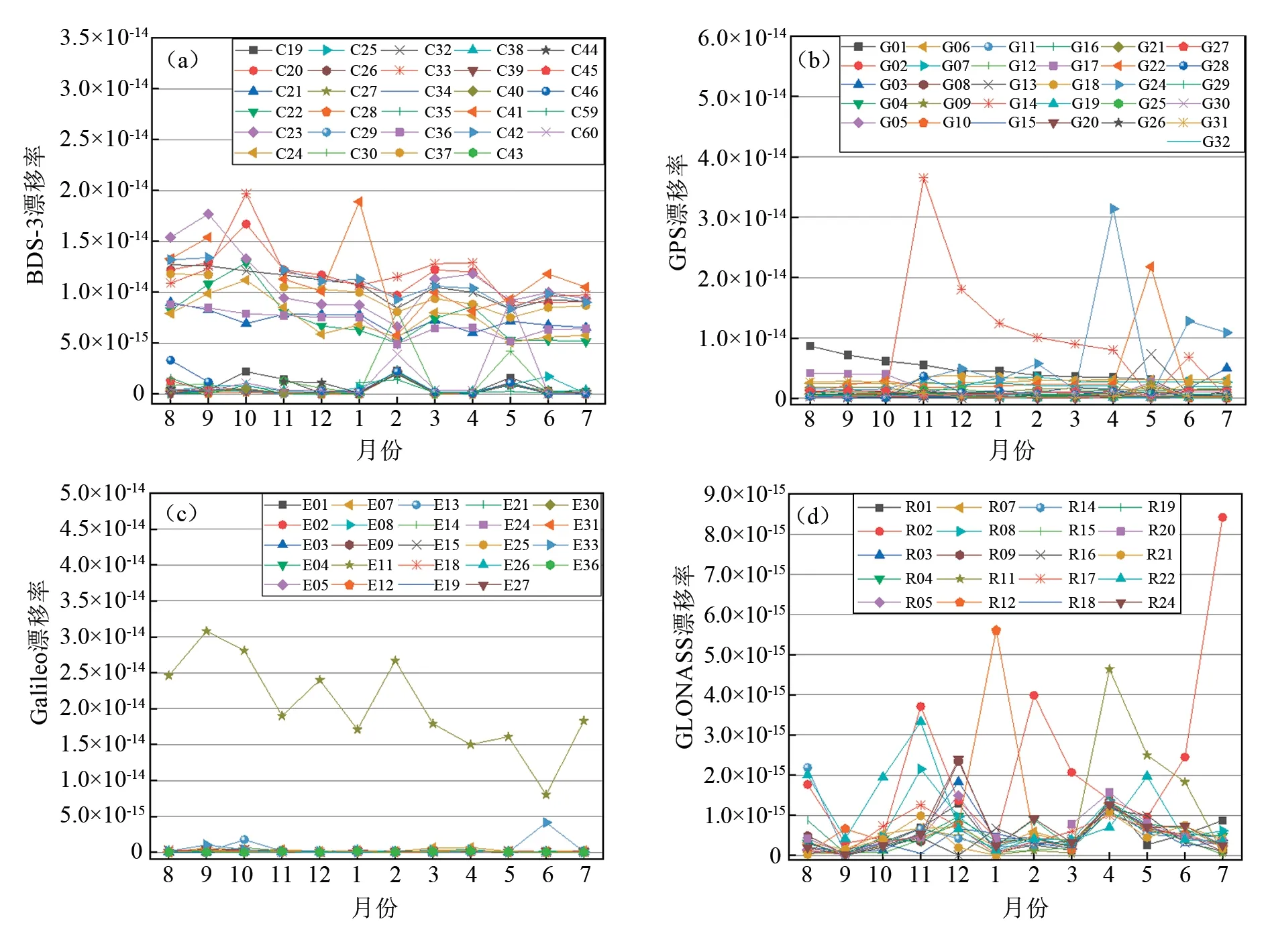
图3 GNSS星载原子钟漂移率Fig.3 Drift rate of GNSS on-board atomic clocks

2.5 稳定度分析

天稳定度（天稳）是描述卫星性能的重要指标。表2、表3根据不同的卫星轨道类型和原子钟类型对BDS-3的频率稳定度进行了分类统计。MEO卫星铷原子钟的千秒稳、万秒稳、天稳分别为3.57×10-14/1 000 s、2.63×10-14/10 000 s、1.15×10-14/d，同轨道卫星氢原子钟的千秒稳、万秒稳、天稳分别为3.21×10-14/1 000 s、2.56×10-14/10 000 s、1.09×10-14/d，说明氢原子钟的短期稳定性、长期稳定性都优于铷原子钟。IGSO卫星氢原子钟的频率稳定度与MEO卫星的氢原子钟相当，优于GEO卫星。

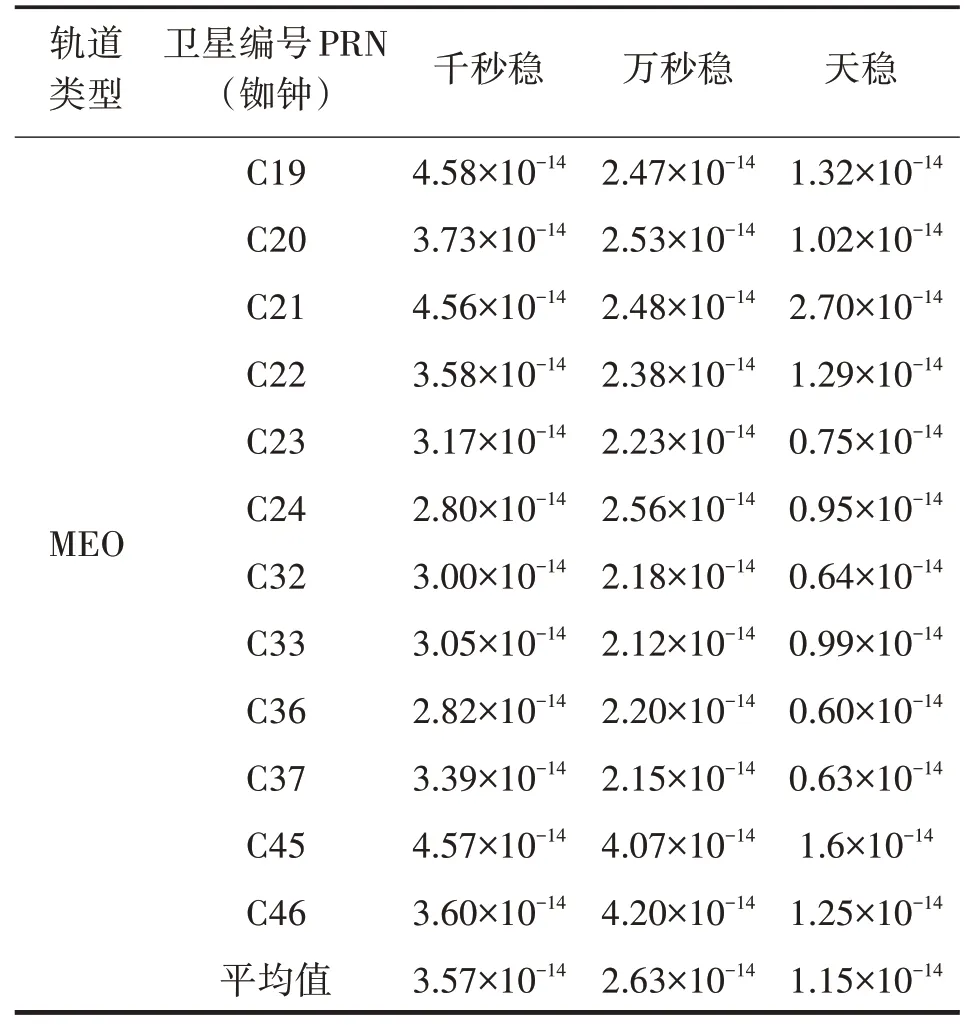
表2 BDS-3哈达玛方差对铷钟的统计结果Tab.2 Statistical results of the Hadamard variance of the rubidium clock of BDS-3

表3 BDS-3哈达玛方差对氢钟的统计结果Tab.3 Statistical results of the Hadamard variance of the hydrogen maser of BDS-3

图4为GNSS星载原子钟频率稳定度月份变化图。BDS-3的MEO卫星铷原子钟稳定度均值为1.15×10-14/d，氢原子钟为1.09×10-14/d，IGSO卫星氢原子钟稳定度均值为9.70×10-15/d。GPS卫星原子钟的稳定度处于1.88×10-15/d~6.24×10-14/d范围内，铷原子钟的稳定度为1.13×10-14/d，铯原子钟稳定度为6.23×10-14/d，其中G08、G24、G28的稳定度较差，明显高于其他卫星。Galileo卫星氢原子钟的稳定度为4.80×10-15/d，频率稳定度在四个系统中最优，E11铷原子钟的稳定度为6.35×10-14/d，比其他卫星高出一个量级。GLONASS卫星的稳定度均值为4.17×10-14/d，在四个系统中的表现最差。以上数据可以看出BDS-3里IGSO氢原子钟的稳定度最优，其次是MEO氢原子钟、MEO铷原子钟、GEO氢原子钟。

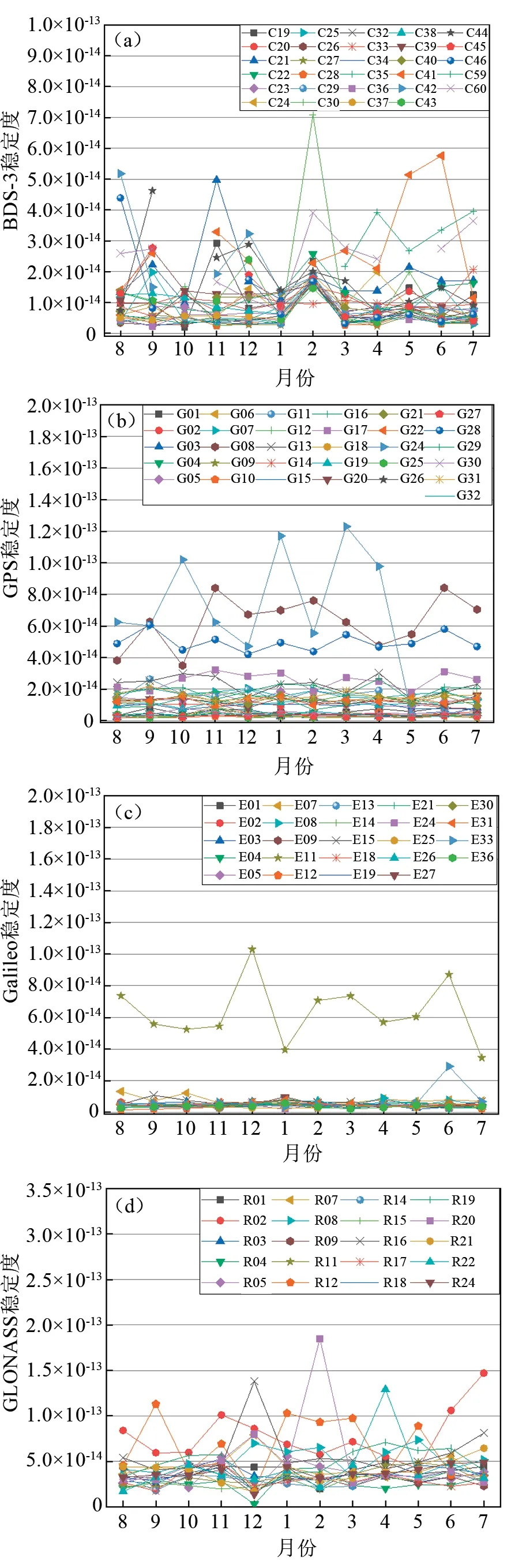
图4 GNSS星载原子钟稳定度Fig.4 Stability of GNSS on-board atomic clocks

3 分析与结论

原子钟是卫星导航系统的核心，根据GBM一年的精密钟差数据，从频率准确度、频率漂移率和频率稳定度三个方面分析星载原子钟的性能，表4给出了分类统计。通过分析GNSS卫星时域稳定性发现，准确度方面BDS-3的MEO和IGSO卫星、Galieo使用氢原子钟卫星、GPS和GLONASS都处于10-12量级，BDS-2和Galileo的铷原子钟处于10-11量级，其中BDS-3的新型铷原子钟较BDS-2铷原子钟有较大提升。BDS-3MEO和IGSO卫星的氢原子钟精度高于GEO卫星。GPS第三代中IIR-M卫星准确度高于IIR卫星，第四代的IIF卫星精度高于第三代卫星，其中铯原子钟的准确度最高。Galileo的氢原子钟优于铷原子钟，E11的铷原子钟在评估时间内的前几个月准确度较差，后期准确度显著提升。GLONASS铯原子钟的准确度高于BDS、GPS、Galileo的原子钟，整体来看GLONASS铯原子钟的精度高于其他系统的氢原子钟和铷原子钟。

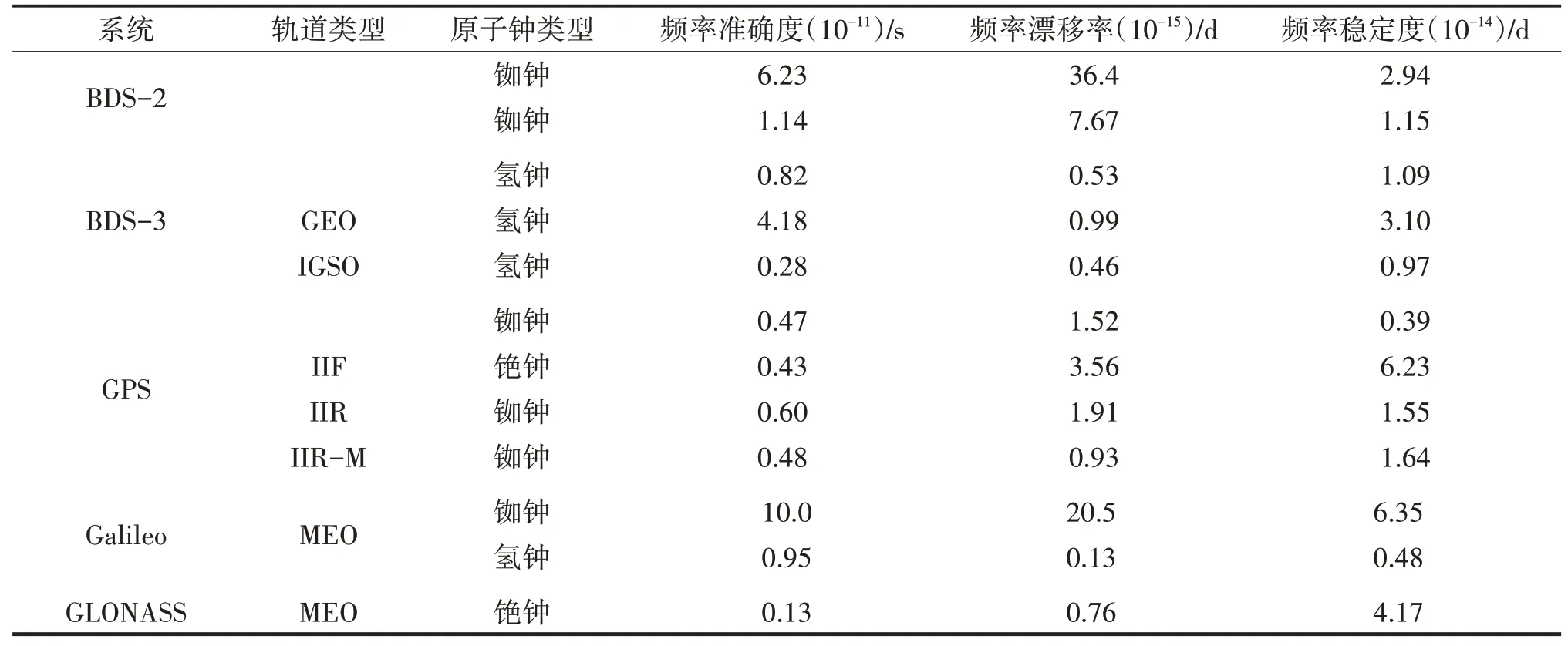
表4 GNSS星载原子钟性能均值Tab.4 Average performance of GNSS on-board atomic clocks

漂移率方面BDS-3和Galileo的铷原子钟日漂移率在10-14量级，氢原子钟在10-16量级，BDS-3的铷原子钟较BDS-2铷原子钟精度提升一个量级，BDS-3氢原子钟漂移率优于铷原子钟，这说明铷原子钟有明显的频率漂移。三种轨道类型的卫星里，IGSO氢原子钟的漂移率最小，GEO氢原子钟的漂移率最大。GPS铷原子钟漂移率优于BDS和Galileo的铷原子钟，其中IIR-M原子钟的漂移率小于IIR卫星。Galileo的氢原子钟的漂移率在四个系统中最小，GLONASS铯原子钟的漂移率与BDS-3氢原子钟相当。

稳定度方面氢原子钟相比于铷原子钟和铯原子钟更稳定，BDS-3的铷原子钟的稳定度较BDS-2提升一倍左右。GPS里最新一代的IIF卫星铷原子钟的表现优于铯原子钟，第三代的IIR和IIR-M卫星原子钟稳定度相当，IIF卫星铷原子钟较IIR和IIR-M有较大提升，IIF卫星的铯原子钟和GLONASS的铯原子钟稳定度略差。Galileo氢原子钟的稳定性与GPS的IIF相当，但其铷原子钟的稳定度较差。

目前BDS-3已全面组网完成，原子钟的性能表现备受关注，本文通过一年的事后精密钟差数据分析了BDS-3、GPS、Galileo和GLONASS星载原子钟的性能表现。结果表明BDS-3的铷原子钟较BDS-2性能提升明显，BDS-3的氢原子钟的准确度和漂移率显著优于BDS-3的铷原子钟，天稳定度方面BDS-3多数氢原子钟可达到10-15量级。BDS-3原子钟天稳定度的平均值最优，其次是GPS、BDS-2、Galileo和GLONASS。对原子钟的性能分析可以为后续卫星导航系统性能的提升提供参考。随着原子钟精度的不断提高，导航卫星的定位与授时精度也会得到进一步提高。