抽运-检测型原子磁力仪对10 kHz正弦交变电流的测量

缪培贤

（兰州空间技术物理研究所真空技术与物理重点实验室，兰州 730000）

0 引言

电磁计量在现代测量技术中有着重要的地位和广泛的应用[1-2]。交流电量计量是电磁计量的重要组成部分[1]，国内已开展了可编程交流量子电压标准的研究[1-4]和交变微弱磁场标准的研究[5]，交流电压和恒定电阻转换可得到交流电流，目前仍未解决毫安甚至微安交流电流的校准和溯源[1]。我国已分别建立基于约瑟夫森效应、量子化霍尔效应和拉莫尔进动效应的量子电压、量子电阻和磁感应强度基准[1-2]，电流单位由电压单位和电阻单位导出[2]。利用高灵敏度的原子磁力仪测量载流标准线圈产生的磁感应强度，可将磁感应强度基准与量子电压基准和量子电阻基准联系起来，其中标准线圈的线圈系数可被溯源至拉莫尔进动效应、约瑟夫森效应和量子化霍尔效应。基于这种考虑，寻找一种自然基准，其物理效应与载有毫安或微安交流电流的标准线圈的线圈系数联系起来，有望实现毫安或微安交流电流的校准和溯源。

磁感应强度基准利用了原子磁矩在静磁场中的拉莫尔进动效应，各种原子磁力仪的工作物质的旋磁比可通过实验溯源至质子旋磁比[6]。在静磁场方向垂直的平面内叠加共振的交变磁场可实现二能级磁共振塞曼跃迁的物理效应[7-9]，该物理效应可应用于毫安或微安交流电流的测量。1954年Rabi等[10]采用旋转坐标系下的经典理论讨论了磁共振塞曼跃迁的物理问题，指出了经典理论表达式和薛定谔方程的等价性。王义遒等[11]编著的《量子频标原理》是国内原子钟研制单位的参考书，书中也利用旋转坐标系推导了二能级磁共振塞曼跃迁的经典理论。作者结合之前的工作[8-9]，进一步阐明磁共振塞曼跃迁的经典理论与抽运-检测型原子磁力仪信号的关联，提出毫安或微安交流电流测量的物理基础，利用抽运-检测型原子磁力仪测量毫安量级正弦交变电流的频率、振幅和相位，通过理论拟合实验曲线初步评估正弦交变电流参数重复测量的相对标准偏差。

1 实验装置及理论分析

1.1 实验装置

正弦交变电流测量装置的示意图如图1所示。将信号源产生的正弦交变电流通入亥姆霍兹线圈和负载中，在磁屏蔽筒内的铷泡区域产生x轴方向的线偏振正弦交变磁场；恒流源的输出端与磁屏蔽筒内的本底磁场线圈相连接，通过调整恒流源的输出电流可改变磁屏蔽筒内z轴方向的本底磁场B0；使本底磁场对应的铷原子拉莫尔进动频率等于正弦交变电流的频率，通过理论表达式拟合磁共振曲线可得到正弦交变电流的频率、振幅和相位信息。可利用抽运-检测型原子磁力仪测量本底磁场[7-8]，上述线偏振的正弦交变磁场即为抽运-检测型原子磁力仪工作时所需的射频场。抽运-检测型原子磁力仪的工作过程是：z轴方向的795 nm右旋圆偏振抽运激光极化原子气室内的铷原子系综，使其磁矩与外磁场平行；抽运激光关闭后，射频场作用π/2脉冲，驱动87Rb原子磁矩进动至与外磁场垂直的平面内；当抽运激光和射频场都关闭时，在x轴方向上利用红失谐6 GHz的线偏振探测激光差分探测拉莫尔进动信号，再用计算机程序算出拉莫尔进动频率和待测磁场值。图1中虚线框部分为原子磁力仪工作时的时序控制，T、t1和t2分别为原子磁力仪的一个工作周期、抽运激光的作用时长和射频场的作用时长，剩余时间则完成自由弛豫信号的探测、采集和数据处理。抽运-检测型铷原子磁力仪的输出信号与原子磁矩在探测光方向上的投影矢量有关[9]，即原子磁矩在x轴方向投影矢量随时间的变化决定了x轴差分信号随时间的波动。当本底磁场对应的铷原子拉莫尔进动频率严格等于正弦交变电流的频率时，连续作用的正弦交变磁场可驱动铷原子磁矩在平行于z轴和反平行于z轴这两种状态之间演化，铷原子磁矩平行于z轴或反平行于z轴时x轴差分信号的振幅趋近于零[7-9]，因此可通过x轴差分信号是否出现波节来判定本底磁场对应的铷原子拉莫尔进动频率是否与正弦交变电流的频率相等。假如信号源连续输出正弦交变信号，时序模块需控制图1中的电子开关来实现射频场的打开或关闭。为了保证正弦交变电流的频率、振幅和相位重复测量时有较好的复现性，原子磁力仪的工作周期T应为正弦交变电流频率的倒数的整数倍。本文实验中选用安捷伦33250A信号源，利用触发功能可实现射频场开关功能，通过设定正弦脉冲的初始相位能保证重复测量时正弦交变信号的相位相同。待测正弦交变电流的频率设定为10 kHz，T设定为100 ms，t1设定为30 ms，通过测量自由弛豫信号来确定本底磁场时，t2设为0.5 ms；测量射频场连续作用条件下的磁共振信号时，t2设为30 ms。恒流源选用是德科技公司的B2912A精密电流源，负载选用零电阻。由于不具备量子电压和量子电阻的量值传递条件，本文利用B2912A精密电流源向亥姆霍兹线圈输入台阶递增的电流，利用无射频场激发的抽运-检测型原子磁力仪[12]测量台阶递增的磁场，线性拟合得到亥姆霍兹线圈的线圈系数为49.08 nT/mA。

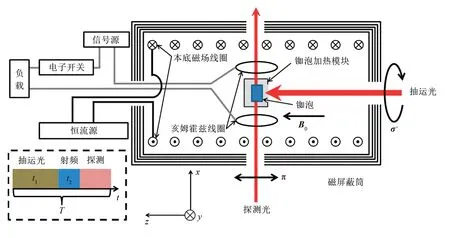
图1 正弦交变电流测量装置示意图Fig.1 Schematic diagram of sinusoidal alternating current measuring apparatus

1.2 理论分析

旋转坐标系中二能级磁共振塞曼跃迁问题的理论分析可参考文献[10]或文献[11]，本文在之前理论分析[9]的基础上进一步完善抽运-检测型原子磁力仪输出信号的理论表达式。当一群原子的波函数相位是一致时（或表述为原子状态是相干时），这群原子可以看成是一个[13]，因此本文首先用单个原子的磁矩来推导二能级磁共振塞曼跃迁的物理过程，考虑原子系综的弛豫后，进一步得出抽运-检测型原子磁力仪输出的磁共振信号的理论表达式。

通过经典力学分析，与原子总角动量F相联系的总磁矩μ在恒定磁场B0中受到力矩L的作用，即：

该力矩使磁矩μ改变方向，并使μ绕B0进动，该物理效应被称为拉莫尔进动效应。设进动角速度为ω0，则可得角动量的运动方程为：

式中：t为时间。

另一方面，角动量变化的动力学方程为

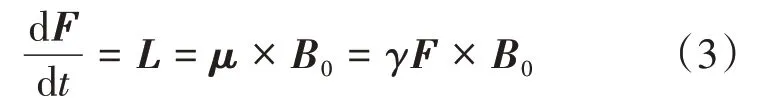
式中：γ为旋磁比，87Rb原子对应的γ/2π的值为6.99583 Hz/nT[14]。由式（2）和式（3）可得：

假设旋磁比γ为正，则B0与ω0的方向相反，实验中保证z轴正方向施加的磁场为正。为方便分析和计算，将矢量投影至基矢{ex，ey，ez}，其中ex、ey、ez分别是平行于x轴、y轴、z轴的单位矢量。ω0的模值为ω0，令ω0=2πf0，其中f0为拉莫尔进动频率，则式（4）中ω0=-ω0ez。

在x轴方向上施加线偏振激励磁场，该线偏振磁场可被看做是左旋圆偏振磁场和右旋圆偏振磁场的叠加，其中与原子磁矩绕外磁场进动方向相同的旋转磁场对磁矩有作用，而与原子磁矩绕外磁场进动方向相反的旋转磁场对磁矩不起作用[10-11]。起作用的旋转磁场的角频率设为ω，强度设为Brf。引入与Brf一起转动的坐标系，转动角速度ω=-ωez，其中ω为ω的大小，令ω=2πf，其中f为射频场频率，也就是待测正弦交变电流的频率。转动坐标系基矢为{ex'，ey'，ez'}，其中ez'与实验室坐标系的ez始终平行，因此ω=-ωez'=-ωez。在转动坐标系中角动量还受到恒定力矩L'=γF×Brf的作用。转动坐标系中矢量的变换关系为

式中：Beff为旋转坐标系中的有效磁场，如图2（a）所示，可表示为：

如图2（a）所示，右旋圆偏振抽运光的作用使μ平行于B0，抽运光关闭后，射频场的作用使μ在转动坐标系中绕Beff进动，随时间演化的章动角为φ。μ与Beff的夹角设为α，μ与B0的夹角设为θ，分析图中的几何关系可得：

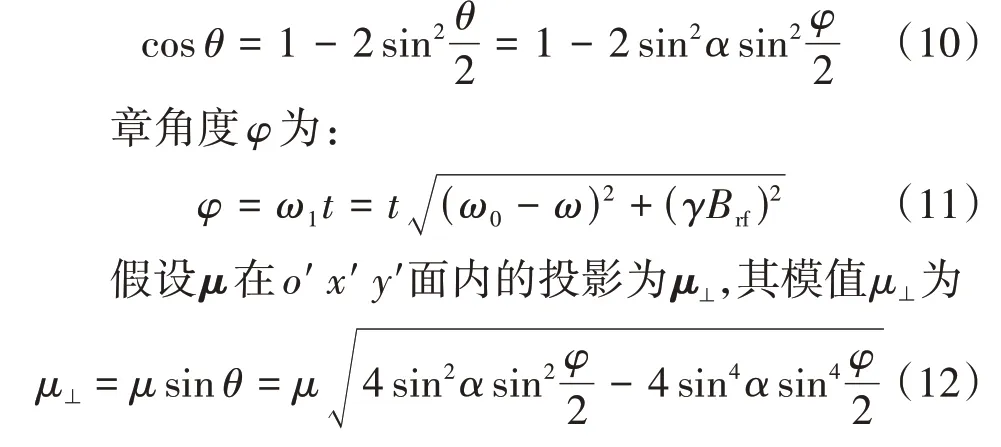
从图2（a）分析，μ在ey'和ex'轴上的投影分量分别为：

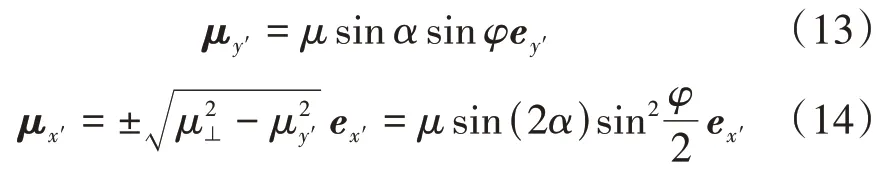
结合图2（a）可判定式（14）的符号：当ω≪ω0且ω可被忽略时，α≈0，μx'的模值取零值；当ω＜ω0且ω不可被忽略时，0＜α＜π/2，μx'的模值大于等于零；当ω=ω0时，α=π/2，μx'的模值取零值；当ω＞ω0且ω0不可被忽略时，π/2＜α＜π，μx'的模值小于等于零；当ω≫ω0且ω0可被忽略时，α≈π，μx'的模值取零值。

分析图2（b）可知，实验室坐标系和旋转坐标系的坐标变换为：

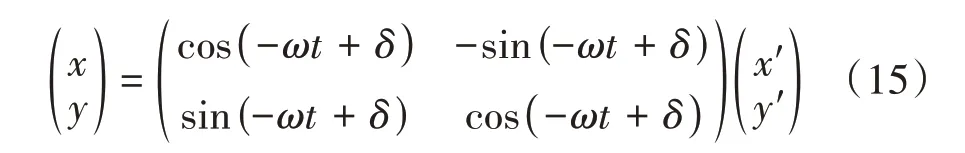
式中：δ为初始时刻旋转坐标系相对于实验室坐标系的角度，该值与射频脉冲的初始相位有关联，t时刻旋转坐标系相对于实验室坐标系转过的角度为-ωt+δ。

因此，μ在实验室坐标系中x轴方向上投影矢量的模值μx为：

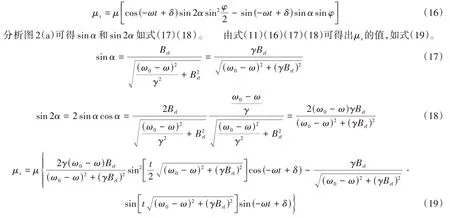
以上经典理论的推导仅针对单个原子，假如一群原子一致进动，上述表达式可拓展到原子系综，理论上所有原子磁矩的矢量叠加形成原子系综的宏观磁矩，但实际中由于气室内铷原子与泡壁、缓冲气体原子、其他铷原子之间的碰撞都有几率改变单个原子磁矩的取向，原子系综的宏观磁化强度随时间呈指数衰减，即原子极化态的弛豫过程。原子磁力仪输出的x轴差分信号的电压值Vx-signal为：

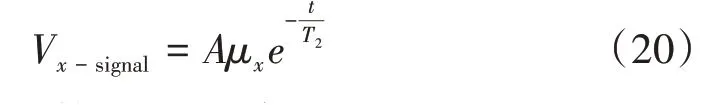
式中：A为比例系数；T2为弛豫时间。

原子磁矩μ在旋转坐标系z'轴和实验室坐标系z轴的投影矢量相同。由式（10）可知，μz的模值μz为：

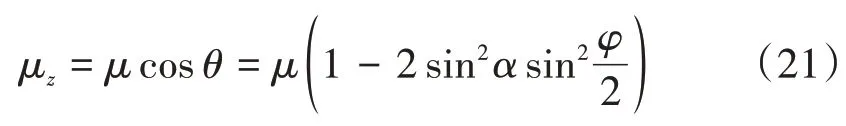
将式（11）和（17）代入式（21）得：

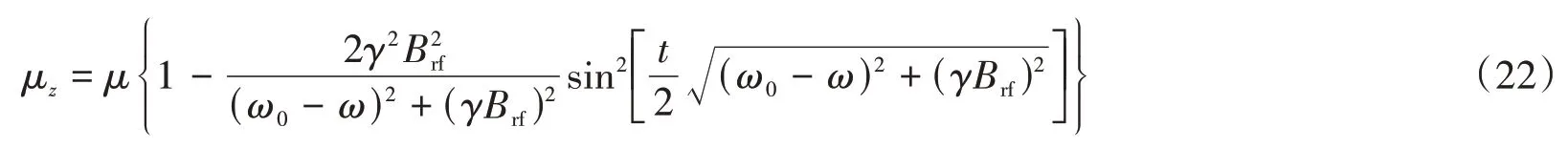
类似于式（20），假如在z轴方向利用失谐的线偏振探测激光差分探测磁共振信号，该信号的电压值Vz-signal为：

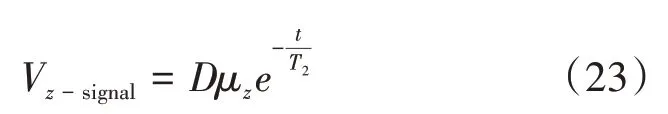
式中：D为比例系数；T2为弛豫时间。

特殊情况下，当ω=ω0时，由图2（a）可知α=π/2。初始时刻转动坐标系中μ与B0平行，随着时间演化，μ绕Brf进动，直至μ与B0反平行；同时实验室坐标系中μ绕着B0进动，因此μ在实验室坐标系中呈现出如图2（c）所示的复杂进动。μ与B0平行代表原子处于低能态，μ与B0反平行代表原子处于高能态，假如87Rb原子与射频场持续相互作用，87Rb原子在两个磁能级之间来回跃迁，x轴磁共振信号会出现诸多波节。共振条件下式（20）和（23）变形为：

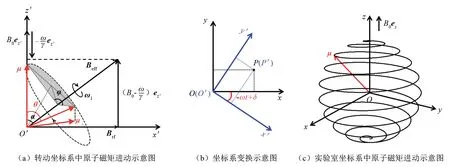
图2 原子磁矩在不同坐标系中进动的示意图Fig.2 Schematic diagram of precession of magnetic moment in different coordinate systems

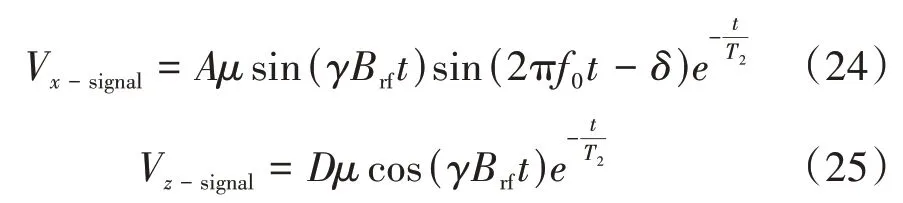
利用式（24）拟合x轴磁共振信号，可获得Brf、f0和δ参数。式（25）描述了二能级磁共振塞曼跃迁的Rabi振荡信号，在图1中额外设计z轴线偏振探测光，通过差分方式可测得该Rabi振荡信号。若忽略式（24）（25）中比例系数和弛豫项的贡献，式（24）中μsin（γBrft）实际上就代表了μ在oxy面内投影矢量的贡献，它与式（25）中μcos（γBrft）有关联，二者平方和正好是μ2；式（24）中sin（2πf0t-δ）项代表了拉莫尔进动效应使μ在oxy面内的投影矢量再次向x轴投影的贡献，实测的磁共振曲线可通过取峰值和谷值来分离sin（γBrft）和sin（2πf0t-δ）的贡献。

抽运-检测型原子磁力仪工作时为了获得高信噪比的自由弛豫信号，一般要求磁共振条件下（ω=ω0）射频场作用π/2脉冲[7-8]，即射频场幅度Brf满足：

式中：Brf的值由射频场的强度决定；tπ/2为射频场作用π/2脉冲的时长。

亥姆霍兹线圈中正弦交变电流信号随时间的演化的表达式为

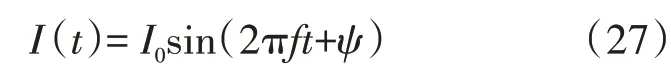
式中：I0为待测正弦交变电流的振幅；ψ为待测正弦交变电流的初始相位。载流亥姆霍兹线圈在其中心位置产生的磁场为：

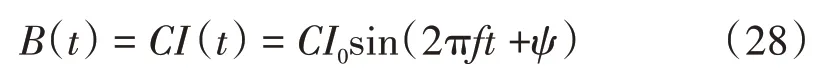
式中：C为亥姆霍兹线圈的线圈系数。

线偏振射频磁场可被看做是左旋圆偏振磁场和右旋圆偏振磁场的叠加，当ω=ω0时，磁共振塞曼跃迁中起作用的旋转磁场的振幅Brf应是振幅B（t）的一半，则正弦交变电流的振幅为：

基于抽运-检测型原子磁力仪工作时序的精确刻度，上述理论基础和实验曲线的拟合参数可分析出式（24）和式（27）中相位δ和相位ψ的关系，即实现了正弦交变电流相位的测量。

2 实验与讨论

设定信号源的输出频率为10 kHz，振幅为760 mV，射频脉冲串初始相位为零；射频场作用时长设定为0.5 ms，调整恒流源的输出电流改变本底磁场，利用原子磁力仪测得拉莫尔进动频率约为10 kHz，磁力仪输出的自由弛豫信号如图3（a）所示，曲线中数据的采样率为5 MS/s；射频场作用时长设定为30 ms时磁力仪输出的x轴磁共振信号的部分实验数据如图3（b）所示，磁共振信号的波节位置是原子磁矩平行于z轴或反平行于z轴的时刻，一个完整的波包代表铷原子经历一次完整的二能级磁共振塞曼跃迁，波包时长对应着射频场π脉冲时长，则π/2脉冲时长约为0.5 ms，此时图2（a）中α=π/2。当ω＜ω0且ω不可被忽略时，图2（a）中0＜α＜π/2，μ将无法进动到z'轴负方向，仅μ与z'轴正方向平行时磁力仪输出的x轴磁共振信号出现波节。当α=π/4时，ω0/γ-ω/γ=Brf，结合式（26），将tπ/2取值为0.5 ms，计算得频率失谐为500 Hz。保持本底磁场对应的拉莫尔进动频率f0为10 kHz不变，射频场作用时长设定为30 ms，射频场频率f为9.9 kH或9 kHz时原子磁力仪输出的磁共振信号如图4所示。对比图4（a）和图3（b），从f0=f的共振条件到f0-f=100 Hz的失谐条件，1 ms位置处从存在波节到波节消失，原因是频率失谐条件下μ无法进动到z'轴负方向。当频率失谐1 kHz时，图2（a）中α＜π/4，则图4（b）中每个包络代表章动角φ变化了2π，而图3（b）中每个包络代表章动角φ变化了π。结果表明，严格的磁共振条件应当综合考虑磁力仪测量的拉莫尔进动频率和磁共振信号出现节点来判断；虽然磁力仪测量的拉莫尔进动频率可从数值上等于射频场频率，但这不是磁共振条件的直接实验证据；仅凭信号出现节点无法准确判断磁共振条件，如图3（b）和图4（b）相似，而图3（b）才严格满足磁共振条件。

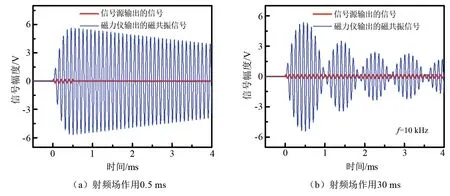
图3 共振条件下原子磁力仪输出的信号Fig.3 Signals acquired by atomic magnetometer under resonance condition

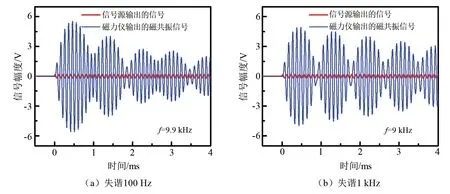
图4 失谐条件下原子磁力仪输出的信号Fig.4 Signals acquired by atomic magnetometer under detuning condition

当实验条件严格满足f0=f，射频场作用时长设定为30 ms，重复测量十条磁共振曲线，截取20 ms的信号数据，并考虑亥姆霍兹线圈中存在暂态过程[9]而去除第一个包络，得到的十条磁共振实验曲线如图5（a）所示，图5（a）的插图为1 ms时长实验曲线的放大图。由于式（24）中有Aμ、Brf、f0、δ和T2这五个未知参量，直接用式（24）拟合图5（a）中的实验曲线时很难收敛，需分步拟合。式（24）可被改写为：

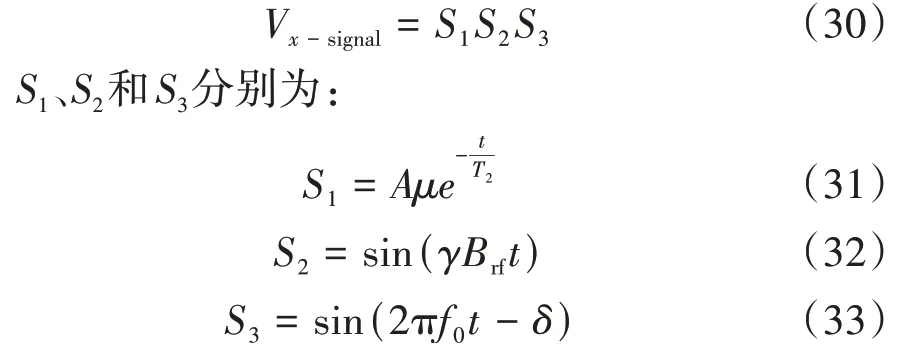
利用计算机编程处理实验数据，对图5（a）中每条实验曲线取一次峰值，得到的曲线如图5（b）所示。再取一次峰值后得到的曲线如图5（b）中插图所示，插图中的曲线用式（31）拟合至收敛，可得拟合参数Aμ和T2。当f0-f＜100 Hz时，计算图5（b）曲线的波谷值之和，调整本底磁场使该波谷值之和最小为f0=f的锁定条件。对图5（a）实验曲线1取峰值和谷值，得到的离散数据点如图5（c）中插图所示，这些离散数据点可分离出两条Rabi振荡曲线，分离的数据点在插图中分别用黑色和浅灰色标记，选取黑色点标记的Rabi振荡曲线作为进一步拟合Brf参数的曲线，选取的所有曲线如图5（c）所示，拟合式为：

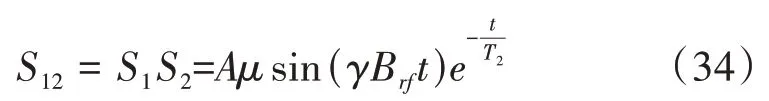
式（34）实际上代表了原子宏观磁矩在oxy面内的投影矢量的演化过程，由该式拟合的Rabi振荡曲线与式（25）拟合的Rabi振荡曲线不同，但明显有互补关系。将之前获得的拟合参数Aμ和T2作为用式（34）拟合图5（c）实验曲线时的固定参数，则可收敛地拟合出Brf。进一步将Aμ、T2和Brf作为固定参数，利用式（24）拟合图5（a）中的实验曲线，则可收敛地拟合出f0和δ，其中一条实验曲线的拟合结果如图5（d）所示。

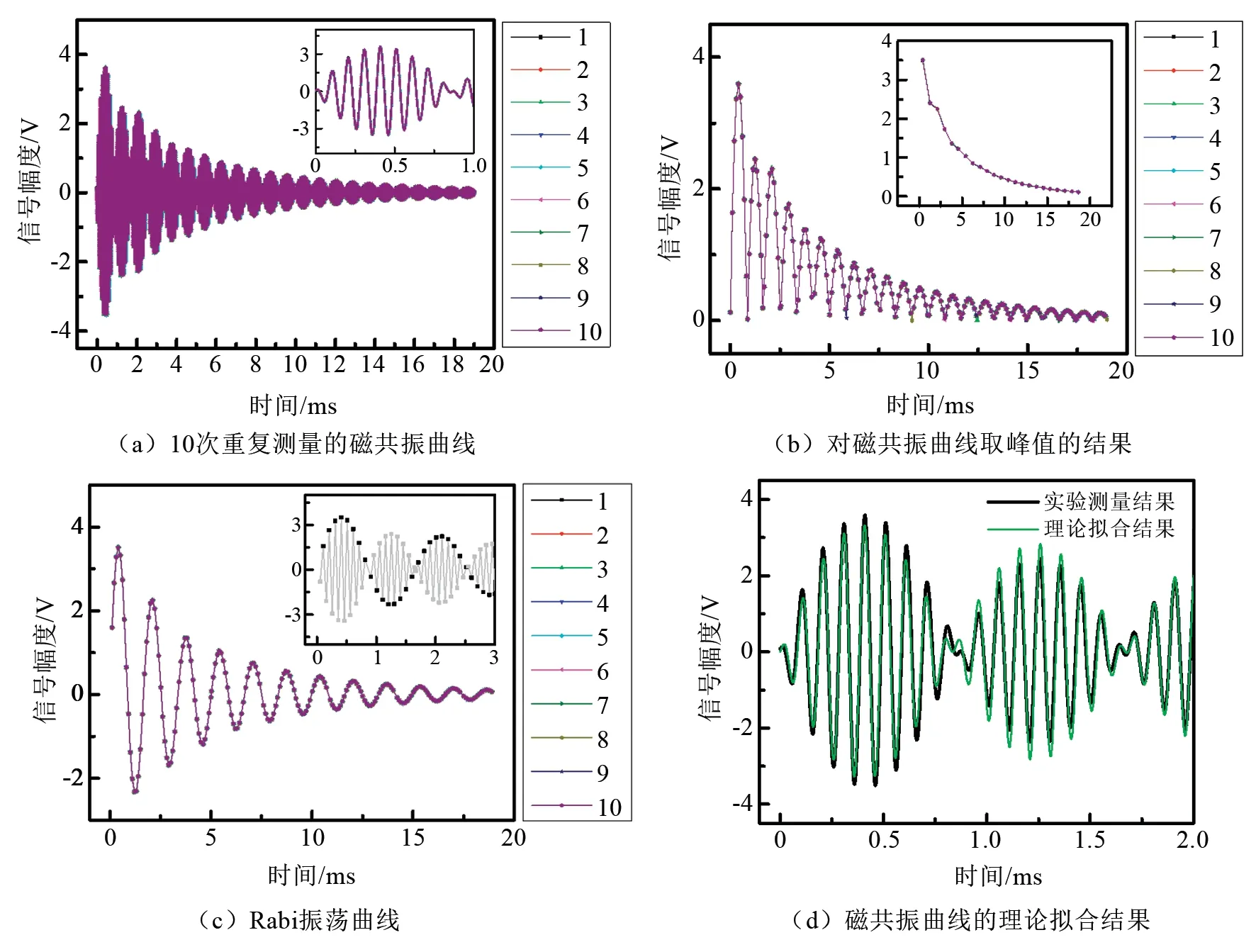
图5 磁共振曲线的拟合过程Fig.5 Fitting process of the magnetic resonance curves

基于上述拟合方法，图5（a）中10条实验曲线的拟合参数如表1所列。表1中同时给出了10次重复测量的标准偏差和相对标准偏差。如果暂不考虑其他实验误差，仅从磁共振曲线的拟合效果来评估对正弦交变电流的测量精度，则正弦交变电流的频率、振幅和相位的相对标准偏差分别为5.4×10-7、2.3×10-5和3×10-3，其中频率f0的相对标准偏差与产生本底磁场的精密电流源B2912A的分辨率有关，也可利用抽运-检测型原子磁力仪测量该电流源的噪声[15-16]。根据拟合参数Brf的平均值和式（29）可计算出亥姆霍兹线圈中待测正弦交变电流信号的振幅I0，已知亥姆霍兹线圈的线圈系数为49.08 nT/mA，则正弦交变电流的振幅为3.49 mA。根据参数δ、抽运-检测型原子磁力仪的时序控制参数和数据截取位置，可进一步分析待测正弦交变电流信号的相位。需要强调的是，假如射频脉冲串的初始相位改变，测量的磁共振曲线也相应地发生变化，导致拟合的参数δ相应地变化[17]。本文利用美国NI公司的PCI-5922数据采集卡采集磁共振曲线，该采集卡的采样率参数以铯原子钟为代表的自然基准标定，因此待测正弦交变电流的频率可通过实验溯源至以铯原子钟为代表的自然基准。

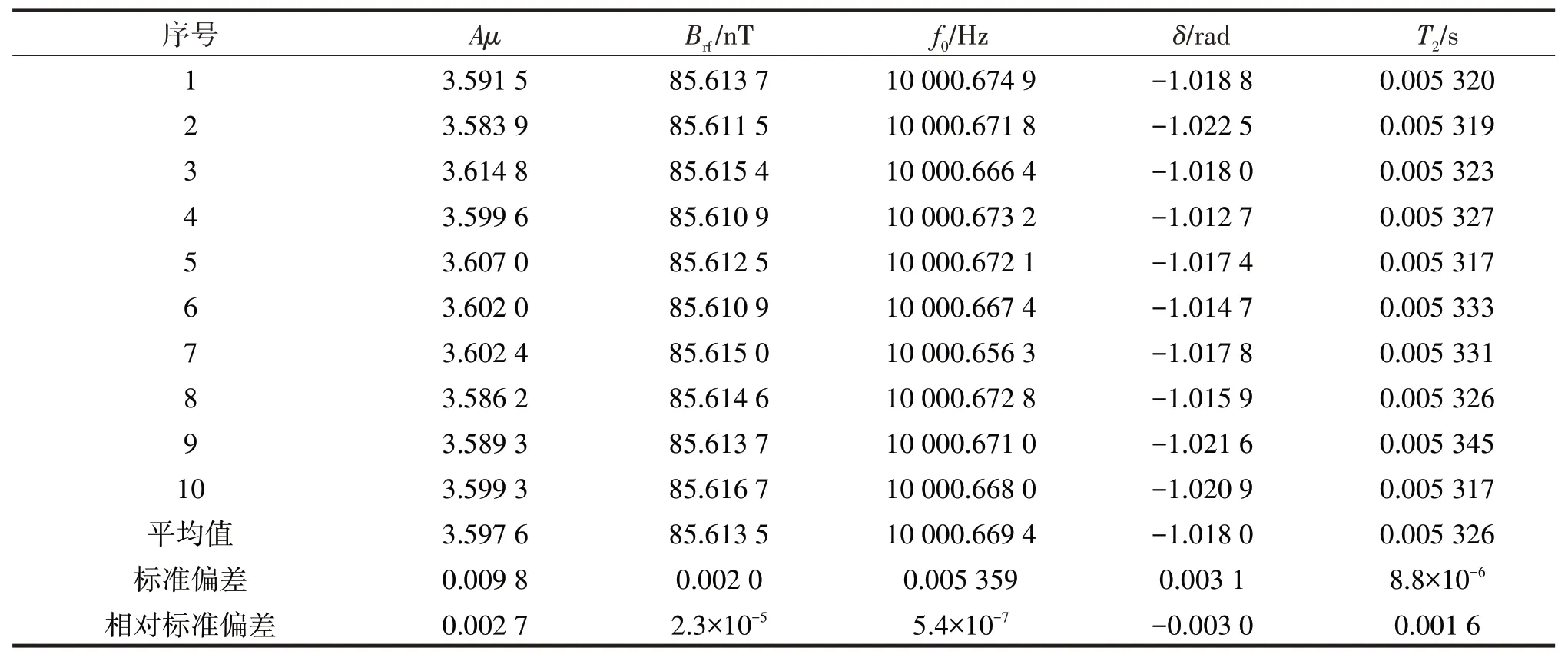
表1 磁共振曲线的拟合参数Tab.1 Fitting parameters of the magnetic resonance curves

上述经典理论和实验结果展示了10 kHz毫安量级正弦交变电流的测量方法，假如需要测量微安量级的正弦交变电流，可适当增加图1中亥姆霍兹线圈的线圈系数，同时增大原子气室的尺寸或气室内镀抗弛豫膜来延长碱金属原子极化态的弛豫时间，通过拟合高信噪比的磁共振塞曼跃迁实验曲线来获得微安量级正弦交变电流的参数。实验中负载选用零电阻，实际应用中负载可为其他元器件或电路模块。图1中的恒流源选用了6.5位的B2912A精密电流源，若需要继续提高对正弦交变电流的测量精度，使表1中各参量的相对标准偏差进一步降低，恒流源可利用原子磁力仪技术降低噪声，Shen等[18]利用Mx光泵磁力仪抑制了电流源的噪声。

3 结论

本文提出利用抽运-检测型铷原子磁力仪测量正弦交变电流的频率、振幅和相位的方法。采用经典理论推导的表达式拟合重复测量的实验曲线，频率、振幅和相位的相对标准偏差分别为5.4×10-7、2.3×10-5和3×10-3，其中频率的相对标准偏差与产生本底磁场的精密电流源的分辨率有关。本文测量的正弦交变电流的频率为10 kHz，当正弦交变电流为其他频率时，测量软件应首先粗锁定，使本底磁场对应的拉莫尔进动频率约等于正弦交变电流的频率，然后基于图5（b）曲线的波谷值之和为最小的判定条件实现精细锁定，使f0与f严格相等，用式（24）拟合磁共振信号得到正弦交变电流的频率、振幅和相位信息。本文虽然提出了基于量子自然基准的正弦交变电流的初步测试方法，但具体进行交变电流计量时还需做大量的工作，分析各种测量过程、实验条件以及电流环路中负载电学参数对交变电流振幅和相位测量不确定度的贡献。随着物理学基础理论的发展和计量水平的提高，未来还需基于理论和实验严格证明仅利用旋转磁场是否能完备描述磁共振塞曼跃迁的物理问题。提出这种顾虑的原因是电磁场中的电场分量和磁场分量是伴生的，然而本文仅讨论了交变磁场与原子的相互作用，缺失了交变电场与原子的相互作用。二能级磁共振塞曼跃迁物理问题中经典理论表达式与薛定谔方程具有等价性，本文基于经典理论和实验结果深入分析了二能级磁共振塞曼跃迁发生的物理过程，未来物理学中“量子”概念与经典物理图像的对应关系是值得深入探讨的一个科学问题，相关研究将显著推动电磁计量事业的发展。