改进的自步深度不完备多视图聚类

崔金荣，黄 诚

（1.华南农业大学数学与信息学院，广州 510642；2.广州市智慧农业重点实验室，广州 510642）

引 言

在近些年提出的聚类方法中，对于同样的一个数据样本可以使用不同的视图来观测和描述。例如，一段电影片段可以用画面和音频两个视图来描述；相同的一张图片可以使用RGB图像和灰度图像来描述。使用多个视图数据之间的互补信息来提升聚类性能，称为多视图聚类。但是在实际情况中，由于人为因素或机器故障，在收集到的数据中可能会出现缺失视图的情况。在带有缺失视图的多视图数据上进行聚类任务，研究人员称之为“不完备多视图聚类”［1］。显然，传统的聚类方法无法进行不完备多视图数据的处理。此外，从缺失的多视图数据中得出不同视图之间的互补信息和一致信息较为困难，这使得不完备多视图聚类成为一项非常具有挑战性的任务。

为了应对不完备多视图聚类的种种问题，在过去的10年间研究人员已经提出了数种不完备多视图聚类模型。这些模型大致可以分为浅层模型与深层模型两类。在浅层模型中，一部分不完备多视图聚类模型设计了基于缺失视图对齐的多矩阵分解模型，以此来学习所有视图的一致特征，并将一致特征用于聚类［2］。但是，这类模型仅适用于两个视图之间的缺失情况。对于具有两个以上视图的任意缺失视图数据，研究人员提出了一系列基于加权多矩阵分解的模型［3］。这些模型大部分是在所有视图的矩阵分解项上添加一些预先构造好的特定于视图的对角矩阵，运用特定的对角矩阵避免缺失视图数据的负面影响。除了这些基于矩阵分解的不完备多视图聚类模型之外，基于多核的聚类模型［4-5］和基于图的模型［6］也开发出了缺失视图的模型。多核不完备多视图聚类模型通常对每个视图相对应的核的缺失部分进行预测和填充，然后从这些填充后的核中寻找所有视图的一致特征。基于图的不完备多视图模型旨在从缺失的多视图数据中建立相似图矩阵并得到多个相似图矩阵之间的一致图特征。相较于基于矩阵分解的模型，基于多核和图的模型可以捕获样本之间的几何结构。此外，有研究人员基于张量奇异值分解并结合多秩张量的高阶相关性提出了一系列不完备多视图聚类模型［7-8］。

以上模型都是基于浅层方法的模型，近年来，由于深度学习模型在提取深层特征中的表现非常出色，因此受到了许多研究人员的青睐。为了进一步提升不完备多视图聚类的表现，有研究人员将深度模型运用于不完备多视图聚类上。例如，有研究人员将自编码器［9］和生成对抗网络（GAN）［10］结合在一起以解决缺失数据带来的负面影响。该模型将两种深度学习模型集成在一起，一方面，自编码器提取深层特征来提升生成对抗网络的训练效果；另一方面，生成对抗网络对缺失数据进行预测与填充来促进自编码器提取深层特征的能力。此外，有研究人员从信息论的角度出发，结合对比学习提出了一种一致表示学习和跨视图数据恢复的理论框架［11］。也有研究人员将单视图的深度聚类模型迁移到了多视图数据中并以此来解决缺失多视图数据情况下的聚类，将“自步学习”的概念引入不完备多视图聚类中，与自编码器相结合，提出了认知不完备多视图聚类网络［12］（Cognitive deep incomplete multi-view clustering network，CDIMC-net），该聚类模型提供了一种基于人类认知的“由易到难”学习策略，增强了深度聚类模型的鲁棒性和聚类表现。然而在CDIMC-net中，作者将缺失视图样本做了“丢弃”处理，将缺失部分以“0”值填充，这样一来该模型在训练时仅利用了未缺失的数据，不仅造成样本数量的减少，同时在特征提取方面仅利用存在的视图，不利于聚类网络的训练。

在CDIMC-net中，作者考虑到了数据之间的几何关系，在训练过程中将样本与样本之间的邻居关系作为约束项加入损失函数，目的是在深度模型在训练中获得更具有区分度的深层特征。受此启发，本文将样本与样本之间的邻居关系用于处理缺失视图的填充，现有的缺失视图处理方法中，通常使用“0”值填充或者均值填充的方法。“0”值填充相当于放弃了那些缺失数据，造成训练时样本量减少。均值填充的方法虽然补全了残缺视图，但是由所有样本计算得到的均值与残缺视图样本值差距较大，在训练时无法保证得到有效的信息。受到邻居关系的启发，在考虑到样本之间的邻居图结构以及多视图数据之间的互补性与一致性，在此基础上，本文使用基于多视图特性的最近邻填充方法对缺失视图进行填充处理，对CDIMC-net进行改进，提出了改进的自步深度不完备多视图聚类（Improved self-paced deep incomplete multi-view clustering，ISPDIMC）。本模型将基于多视图特性的最近邻填充方法、多视图的自编码器、多视图数据的一致性潜在特征、图嵌入策略和基于人类认知的“自步学习”K-means聚类网络这些策略和方法集成到一个深度模型中。合理运用以上策略提升不完备多视图数据的聚类表现。

本文主要贡献如下：

（1）提出了一种新颖深度不完备多视图聚类模型，可以灵活处理各种数据缺失的情况，提升了不完备多视图聚类的鲁棒性与表现效果。

（2）提出的深度不完备多视图聚类模型中使用基于多视图特性的最近邻填充方法，充分利用了各个视图潜在的互补信息，让缺失视图的填充值与原样本值更加相近，并用实验证明了这种基于多视图特性的最近邻填充方案的合理性。

1 相关工作

1.1 K-means聚类算法

K-means［13］是聚类算法中的经典算法，其算法的主要思想如下：对于给定的数据集{X}∈Rm×n，其中包含n个样本，每个样本的特征数为m，以欧式距离为度量比较样本之间的近似程度，依照样本之间的近似程度将数据集划分以K个聚类簇中心{C}∈Rm×k为基点的K个簇，让属于同一个簇的样本尽量紧密的围绕在簇心周围，而不同簇之间的距离应尽量的大，表示为

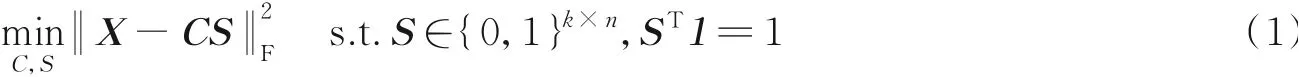
式中：S表示指示矩阵，其中si，j=1表示编号为i的样本属于第j个簇；1表示一个由全1元素组成的向量。

1.2 自编码器

自编码器是一种经典的神经网络模型，通常运用在自监督学习中。其基本思想是通过神经网络不断进行自监督训练让输出的重构样本接近输入的样本。本文中使用的是自编码器是欠完备自编码器，它的内部包含3个部分：编码器fEN()、隐藏层z和解码器fDE()。其中编码器z=fEN(x)对输入的样本进行处理，之后将处理后样本输入隐藏层z，隐藏层的维度通常比输入样本的维度要小，之后将隐藏层的特征通过解码器xˉ=fDE(z)进行输出得到重构样本，通过这样先降维后升维的训练方法，迫使自编码器的隐藏层中要学习到输入样本最具有区分性的特征，其过程可以表述为

1.3 自步学习

“自步学习”［14］用于模拟人类学习新知识的过程：从简单到困难。当给出一些新任务时，人类往往首先选择最简单的任务。当对任务的认知有所提升后，处理难度更高一层的任务，在不断加强任务难度的同时获得更多的知识。在这个不断学习的策略下，可能会获得关于这个任务的所有知识。这种基于人类认知的学习策略被认为是一种有效的训练方式。因为该策略的优异表现，“自步学习”已经被广泛应用于机器学习任务中，如人重识别［15］、分类［16］以及人脸识别［17］。本文在聚类阶段使用“自步学习”策略进行训练，将那些分布于簇中心周围的样本被认为是“简单任务”，而将那些分布于簇边界的样本被认为是“困难任务”。

2 本文方法

本文提出的ISPDIMC模型中首先利用多视图特性选择有效的数据对缺失数据进行填充，之后进行预训练和微调两个阶段，其中预训练阶段为多视图自编码器的自监督训练，并在其中加入了一致潜在特征融合层，目的是寻找到有效的隐藏层特征。而微调阶段则是运用包含“自步学习”的聚类策略，对隐藏层特征进行微调和聚类，使得到的隐藏层特征更适用于不完备多视图聚类任务。

2.1 相关定义

给定一个包含l个视角的数据集{X}(v)∈Rmv×n，其中mv表示各个视图的特征维度，n表示样本个数。在该数据集中，缺失的样本统一用“NaN（Not a number）”来表示。为了表示各个视图上样本的缺失情况，在每一个视图上设置一个对角矩阵W(v)。其中表示该视图上的样本是存在的。与多视图聚类的目的一致，不完备多视图聚类的目的是将n个样本划分为c个簇。

2.2 预训练阶段

基于多视图特性的最近邻填充。根据多视图的一致性与互补性原则。如果两个样本在某一视图上是邻居关系，那么它们在另一视图上应仍保持邻居关系。基于这一假设，在每个缺失视图上都构造出未缺失样本之间的近邻图，如果在视图i上的样本是缺失的，那么将按照邻居的顺序，从第一邻居开始，依次搜索未缺失视图相同序号的邻居，使用邻居顺序和视图顺序最靠前且在视图i上未缺失的样本对缺失样本进行填充。

多视图自编码器与潜在特征融合。对于每一个视图的数据，分别使用自编码器进行潜在特征的学习。经过编码器后，可以得到各个视图的潜在特征{h1，h2，h3，…，hl}。在本文中，对各个视图的潜在特征进行融合获取不同视图之间的一致潜在特征表示

式中：h*表示一致潜在特征；l表示多视图数据集的视图数量。在得到了一致潜在特征之后，将一致潜在特征输入解码器中。利用解码器输出的重构样本和编码器的输入样本进行自监督学习。

图嵌入策略。受到来自子空间学习领域的假设启发［18］：如果高维空间中的一对样本距离很接近，那么从中提取的低维潜在特征应该在低维空间中也很接近。为此，通过如下策略建立邻居关系图

式中G∈Rn×n表示最近邻图关系的矩阵。图矩阵定义如下

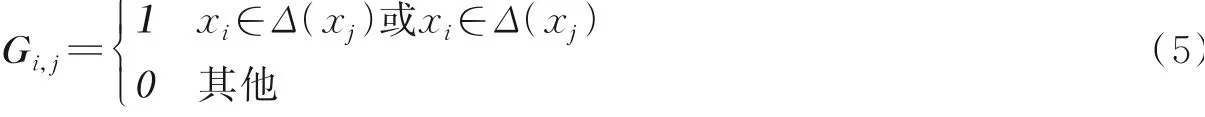
式中Δ(xi)表示欧氏距离度量下样本xi的最近邻。在后续的实验中，将此图嵌入策略应用于预训练阶段和微调阶段。

目标函数。在预训练阶段，ISPDIMC将自编码器的重构样本误差和图嵌入策略相结合，构成预训练阶段的目标函数

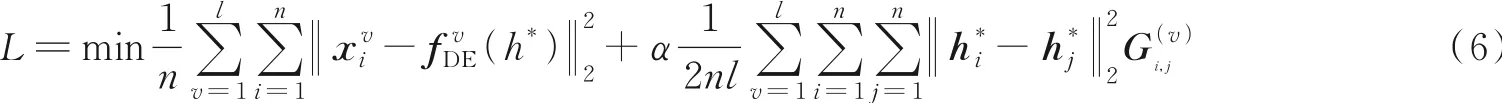
式中：h*由式（3）计算得到；α为图嵌入策略的超参数。

图1展示了预训练阶段的网络结构。

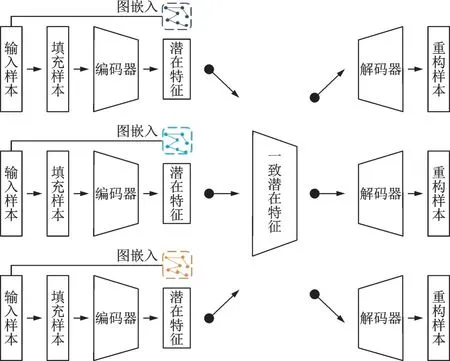
图1 预训练阶段示意图Fig.1 Illustration of pre-training phase

2.3 微调与聚类阶段

通过预训练阶段后，自编码的隐藏层可以获得有效的潜在特征，但是这些潜在特征可能并不适用于不完备多视图聚类任务。对此，受到相关深度聚类算法的启发，在微调阶段将预训练阶段训练好的自编码器的解码器部分放弃，将编码器部分与聚类层相连，利用一致潜在特征进行聚类任务，而聚类的结果又将反馈回指导编码器的训练。

对一致潜在特征进行微调，使其能更好地适应不完备多视图聚类任务。本文在微调阶段采用“自步学习”K-means策略，对隐藏特征进行优化与聚类。

自步学习K-means策略。受到人类认知假设的启发，遵循“由简单到困难”的原则，在聚类时一开始不使用全部样本进行聚类，而是选择靠近聚类簇中心的一部分样本进行聚类，在训练时不断增加样本数量，通过这样的策略，尽可能减少那些分布在聚类簇边缘的样本的负面影响，自步学习K-means策略的目标函数如下［19］

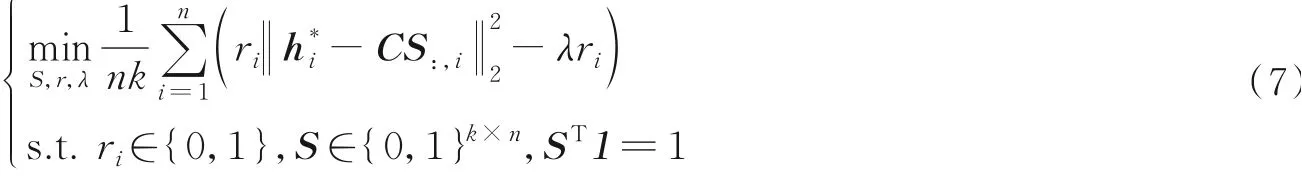
式中：C表示聚类簇中心矩阵；S表示聚类结果指示矩阵。与传统的K-means算法不同，自步学习Kmeans策略在优化时固定了聚类簇中心，这一做法主要时为了避免在训练时所有样本收敛到一起。ri表示各个样本的权重ri∈{r1，r2，r3，…，rn}∈Rn，λ表示从所有样本选取样本所占的比重。

一般来说，为了达到逐渐增加训练样本进入训练的目的，λ应伴随训练次数的增加而增大，但不同训练集，样本数量的不同，较难使用统一的数值来确定λ的成长速度。在自步学习K-means策略中，采用如下方法来自适应调整与增加λ的值

式中：Lt表示在第t此迭代中的损失；T表示总迭代次数；μ(Lt)和σ(Lt)分别表示损失的平均值和标准差。经过式（8）的定义，λ可以灵活地适用于不同数据集与任务。

目标函数。在微调阶段，ISPDIMC将自步学习K-means策略误差和图嵌入策略相结合，构成微调阶段的目标函数

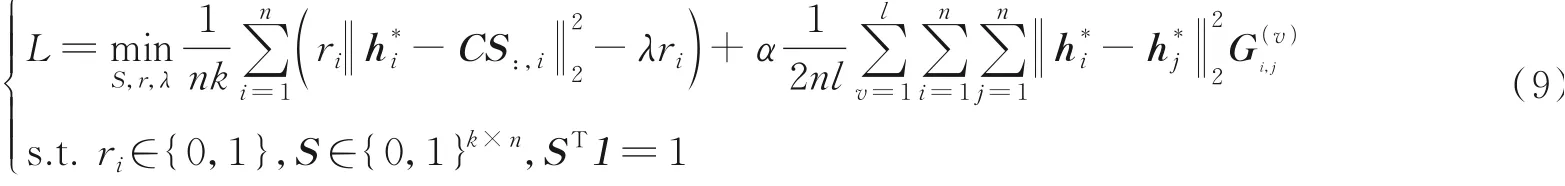
2.4 参数更新与优化

与大多数自编码器的训练方法一样，预训练阶段可以直接用随机梯度下降法（SGD）和反向传播进行优化。本节中重点关注微调阶段的参数更新与优化，交替优化式（9）中的聚类指示矩阵S，各样本权重r以及编码器的参数。

固定编码器参数调整S。当编码器参数固定时，输入样本经由编码器得到的隐藏层一致特征h*是确定的。在聚类簇中心固定的情况下，得到聚类结果S为

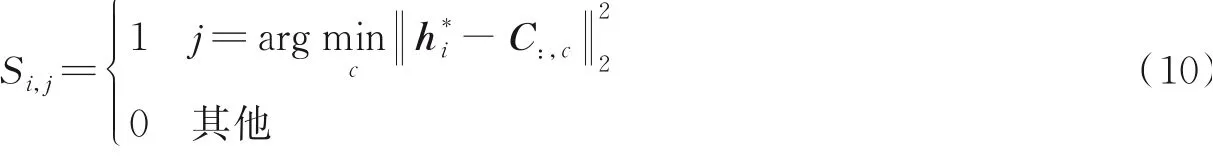
固定编码器参数和S调整r。当编码器参数和聚类结果S都固定时，根据每一个样本与其聚类中心的距离大小来调整样本的权重

式中λ由式（8）计算得到。

固定S和r调整编码器参数。聚类结果S和权重参数r固定时，对于编码器来说就变成了有监督训练，可以依靠SGD和反向传播算法对各个视图的编码器参数进行更新。

停止训练。为了更好地判断训练是否已经收敛，规定当两次迭代之间的聚类结果S变化小于阈值δ停止训练。计算标准如下

式中：St和St-1是在第t次迭代和第t-1次迭代中预测的聚类结果，在本文实验中将δ设置为1e-7。

图2展示了微调阶段的网络结构。

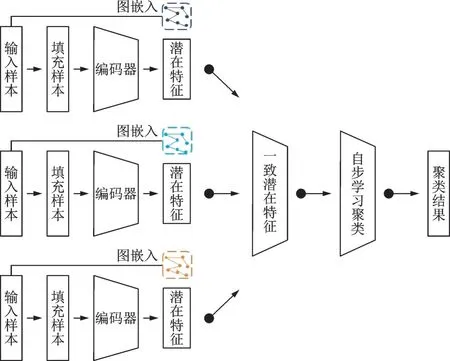
图2 微调与聚类阶段示意图Fig.2 Illustration of fine-tunning and clustering phase

2.5 模型预处理

一般来说，深度学习模型在训练时对数据进行分批处理，本文提出的方法中在训练时不仅要加载数据，而且还要加载由数据计算出的最近邻图矩阵，这样一来，传统的批处理方法将会破坏最近邻图矩阵中携带的数据几何结构信息。为了将批处理中的每个最近邻矩阵的子矩阵能够携带尽可能多的几何结构信息，对数据集进行如下预处理：

（1）基于多视图特性的最近邻填充。通过每个视图的对角矩阵W(v)得到每个视图的缺失样本信息。对每个视图的未缺失样本分别计算它到全体未缺失样本的欧式距离，得到距离矩阵后将其排序，这样就能得到每个未缺失样本的邻居关系。如果在视图i上的样本是缺失的，那么将按邻居的顺序，从第一邻居、第二邻居，……，依次搜索未缺失视图上相同序号的邻居，将邻居顺序以及视图顺序最靠前且在视图i上未缺失的样本对缺失样本进行填充。

（2）数据从新排列与最近邻计算。来自同一聚类簇的样本更有可能是邻居。出于这一假设，先对所有样本进行一次K-means算法，利用K-means计算出的预测标签对样本进行重新排序，在排序后的样本上计算最近邻图。这样一来，在批处理时每一个最近邻子图上将会携带更多的样本间几何关系信息。其步骤为：①预训练：将将所有填充后的视图的特征拼接到一个视图中；②在拼接视图上执行K-means算法；③根据聚类结果对数据重新排序，将分到同一聚类簇中的样本放在一起；④根据式（5）从重新排序的数据构造最近邻图。经过最近邻填充之后，被填充后的值在没有图嵌入策略的限制下在它们的低维特征也可以很接近，为了最大化图嵌入策略的作用，在对角矩阵W(v)的指导下，选择计算每个视图未缺失样本之间的最近邻图，以此来达到更好的训练效果。

经过重新排列之后的数据集定义为{Y}(v)∈Rmv×n。同时计算新的缺失指示对角矩阵Wˉ(v)以及最近邻图

2.6 模型训练

预训练。在预训练阶段，使用SGD对重新排列后的样本进行预训练处理。预训练阶段的批处理表示如下

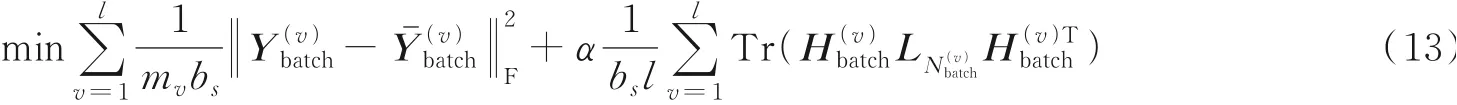
微调。对于微调阶段，将该阶段的详细步骤记录在算法1中。

算法1ISPDIMC的微调阶段算法

输出：聚类指示矩阵S。传入预训练网络得到同一隐藏特征H*，在统一潜在特征上进行K-means算法得到聚类中心矩阵C和初始聚类分布矩阵S，将所有样本的权重向量r置为1。

②fortin｛1，2，…，T｝do

③forjin｛1，2，…，Maxiter｝do

④批处理更新编码器参数

⑤end for⑥如式（10）、（11）和（8）更新参数

⑦if满足式（12）then

⑧停止训练

⑨end if

⑩end for

⑪returnS

3 实验验证

3.1 数据集

本文提出的ISPDIMC方法将在表1列出的3个数据集上进行评估：

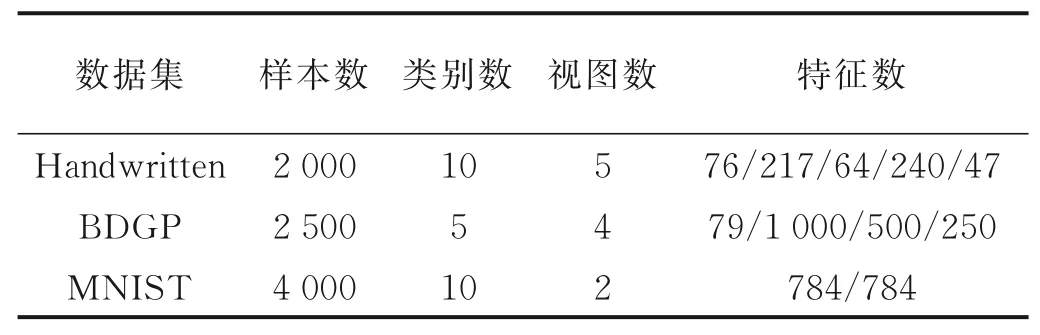
表1 数据集信息Table 1 Information of datasets

（1）Handwritten［20］。该数据集为手写数字图片数据集，其中包含10个数字（即0～9）的2 000个样本，其中包含5个视图特征，分别是傅里叶系数特征、轮廓特征、Karhunen-Love系数特征、Zernike矩特征和像素均值特征。

（2）BDGP［21］。该数据集为伯克利果蝇基因组计划基因表达模式数据库，该数组集包含5个类别，其中每个类别有500个样本，共2 500个果蝇胚胎样本。每个样本包含4个视图特征，即纹理特征和从侧面、背部和腹部图像中提取的3种视觉特征。

（3）MNIST［22］。该数据集为知名的手写数字数据集。其中包含了手写数字0～9共4 000个样本。每个样本包含2个视图特征，分别是像素特征和边缘特征。

3.2 不完备多视图数据集构造

由于以上3个数据集都是完整数据集，为了方便进行实验与对比，采用以下方法来构造不完备多视图数据集：对于拥有两个以上视图的数据集，在所有样本至少保留一个视图的条件下，从每个视图中分别随机删除10%、30%、50%的样本。对于MNIST数据集，保留10%、30%、50%的样本作为视图完整的成对样本，余下样本作为单视图样本处理，即余下样本中的一半样本只有第一视图，另一半样本只有第二视图。

3.3 对比方法与参数设置

用来对比的方法包括2类。第1类为浅层模型中3个具有代表性算法：双对齐不完备多视图聚类（DAIMC）［23］、单趟不完整多视图聚类（OPIMC）［24］和在线不完整多视图聚类（OMVC）［25］。第2类为深层模型：基于一致性生成对抗网络的缺失视图聚类（PVC-GAN）［10］、认知深度不完备多视图聚类网络（CDIMC-net）以及在预训练网络得到的一致潜在特征上运用K-means算法（K-means on consistency hidden features，KoCHF）。其中OMVC对缺失值使用均值填充，DAIMC、OPIMC和CDIMC-net对缺失值使用“0”值填充。PVC-GAN只能运用在两个视图的数据上，在实验中仅在MNIST数据集上进行对比。在参数设置方面，编码器部分由全连接神经网络构成，每层的神经元数量为［Input，0.8Input，0.8Input，1 500，10］，其中Input为输入样本的维度。解码器部分是编码器部分的镜像，每层神经元个数为［10，1 500，0.8Input，0.8Input，Input］。每一层之间的激活函数都使用非线性激活函数“ReLU”。在预训练阶段，采用“SGD”优化器对网络进行优化。在微调阶段，采用“Adam”优化器对网络进行优化。

3.4 评价指标

本文采用聚类精度（Acc）和归一化互信息（NMI）这两种常用的聚类评价指标对不同方法进行评估［12］。

聚类精度的计算公式为

式中：t表示样本所表示的真实类标签；p表示经过聚类算法后得到预测类标签；函数g表示真实类标签与预测类标签的映射关系。函数δ()表示二值指示函数，当p等于g（t）时函数值为1，p不等于g（t）时函数值为0［26］。

归一化互信息度量的计算公式为

式中：MI表示互信息；H表示信息熵［27］。

以上两个评价指标的取值皆为区间［0，1］，指标越高代表该算法的聚类效果更佳优秀。

3.5 实验结果与分析

表2展示了各算法在3个数据集上不同缺失率和成对率在评价指标Acc和NMI的对比结果，其中粗体数字标志出了最优结果，下划线数字标志出了次优结果。

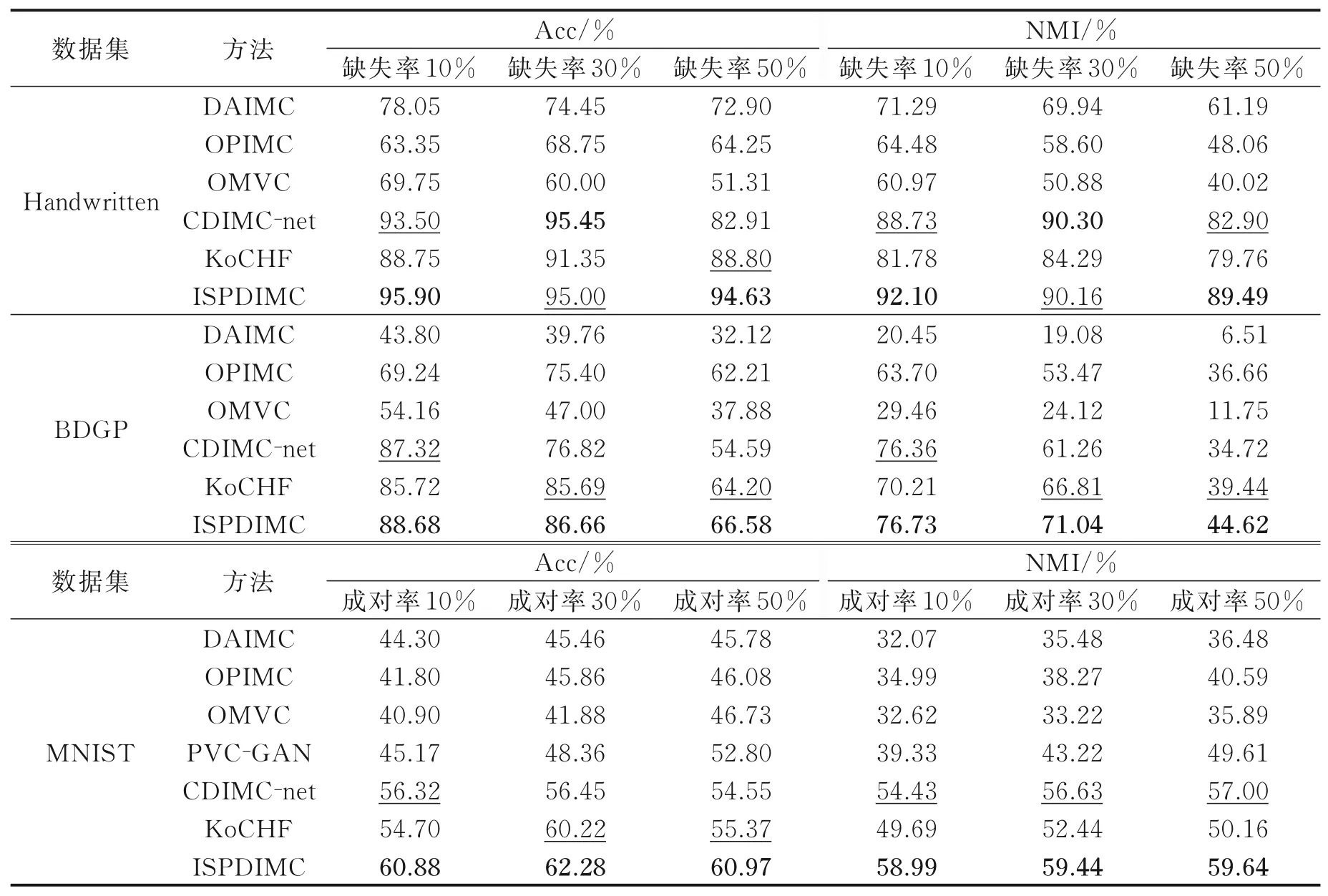
表2 不同方法在3个数据集的Acc和NMI对比Table 2 Comparison of Acc and NMI on three datasets

由表2可知：（1）运用了深度模型的不完备多视图聚类方法在不同的数据集和缺失率上的聚类评价指标结果都是最优或次优，这表明了深度聚类模型对比传统浅层模型在聚类表现上有巨大提升；（2）随着视图缺失率的增加，所有对比方法的聚类评价指标都出现下降的情况，这表明视图的缺失对多视图聚类带来了负面影响；（3）对于使用“0”值或均值填充的方法来说，ISPDIMC使用基于多视图特性的最近邻填充方法，有效减少了样本缺失带来的负面影响，特别是在Handwritten和BDGP数据集上，当缺失值为50%时，对比其他方法，ISPDIMC的聚类指标下降的最少；（4）在多个实验中，ISPDIMC和Ko-CHF得到的实验结果超越了CDIMC-net，这表明了运用基于多视图特性的最近邻填充方案对提升缺失多视图聚类的性能是有帮助的。

3.6 超参数分析

为了探究超参数的设置对聚类结果的影响，在Handwritten和BDGP数据集上，在缺失率为10%的情况下，对微调阶段的图嵌入系数α和学习率进行调整，观察上述2个超参数对聚类结果的影响。具体地，将图嵌入系数α和学习率依次设置为［1e-3，5e-4，1e-4，5e-5，1e-5］，之后将它们的聚类指标Acc和NMI进行对比，结果如图3所示。

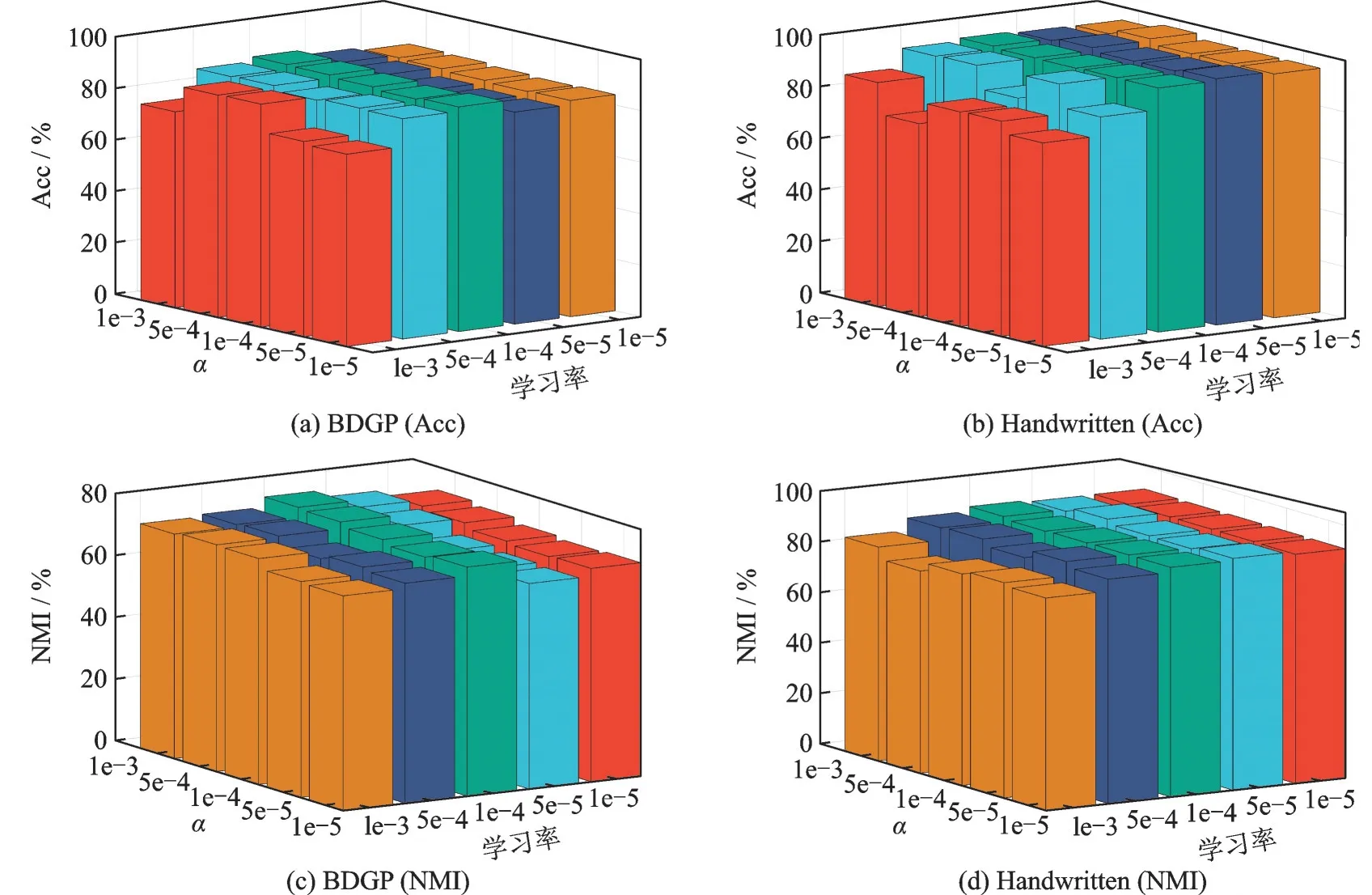
图3 不同图嵌入系数和学习率下的Acc和NMIFig.3 Acc and NMI under different graph embedding coefficients and learning rates

可以看出，学习率设置为［1e-3，5e-4］时，Acc和NMI低于将学习率设置为［1e-4，5e-5，1e-5］的表现。同时，将图嵌入系数α设置为［1e-4，5e-5，1e-5］时表现更优秀。综合2个数据集上Acc和NMI的比较，建议将图嵌入系数α和学习率设置为［1e-4，5e-5，1e-5］。

3.7 消融实验

本文提出的模型中综合运用了多种策略，为了探究每一种策略对聚类效果的影响，将模型退化为缺少预训练的情况、缺少自步学习的情况以及缺少图嵌入的情况，在Handwritten和BDGP数据集上进行不同样本缺失率下的实验。结果如图4所示。由图4可以看出，本文提出的模型表现最佳，缺少了预训练的模型表现最差，这表明了预训练在本模型中十分重要。

图4 不同策略对聚类效果的影响Fig.4 Influence of different strategies on clustering

3.8 训练收敛性分析

图5为ISPDIMC在Handwritten和BDGP数据集上不同缺失率的情况下，在微调阶段的损失随迭代次数的变化情况。由图5可看出，损失在最初的几轮迭代训练中快速下降，然后下降速度放缓，最后趋于稳定。

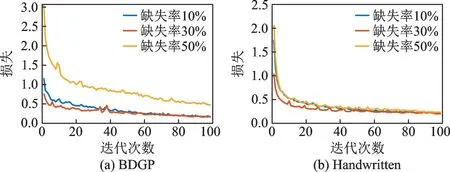
图5 损失随迭代次数的变化情况Fig.5 Variation of loss with the number of epochs

图6为ISPDIMC在Handwritten和BDGP数据集上缺失率为10%的情况下，评价指标Acc和NMI随迭代次数的变化情况。由图6可看出，总体上Acc和NMI在开始几轮的迭代训练中持续上升，最后逐渐趋于稳定的状态。

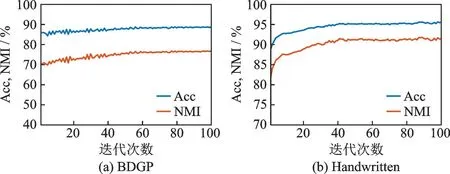
图6 Acc和NMI随迭代次数的变化情况Fig.6 Variation of Acc and NMI with the number of epochs

由以上的训练收敛性分析可知，ISPDIMC在不同缺失率的情况下都可以在经过训练之后达到一个较为理想的稳定状态。

4 结束语

本文提出改进的自步深度不完备多视图聚类（ISPDIMC），使用基于多视图特性的最近邻填充策略将缺失多视图数据以合理的数值进行填充之后，使用自步学习策略对多视图数据进行聚类分析。ISPDIMC包含两个阶段：第1阶段通过基于多视图特性的最近邻填充将缺失视图样本进行补全，之后以自监督的方式进预训练，运用合理方案将多视图潜在特征融合后获取一致潜在特征；第2阶段通过自步学习K-means聚类方案对数据进行聚类分析。同时，在上述两个阶段都加入图嵌入策略来保持样本之间的几何关系。在3个公开的数据集上进行实验，表明了ISPDIMC以更为合理的数据填充方式减小了缺失样本带来的负面影响，同时也提升了聚类与泛化性能。消融实验表明预训练阶段直接影响微调与聚类阶段的表现，今后将会探究更有效的缺失值填充方案与特征融合机制，用于减少缺失视图带来的负面影响，挖掘多视图数据之间更深层次的潜在互补信息，以更加鲁棒的一致潜在特征进行聚类，探索更为先进的不完备多视图深度聚类算法。