耐碱玻璃纤维ECC复合材料受压应力-应变关系

张 勤，朱潇鹏，代欢欢，李 振，叶涛萍，刘荣浩

(1.河海大学 土木与交通学院，江苏 南京 210098；2.中建二局第一建筑工程有限公司，北京 100176；3.江苏大学 土木工程与力学学院，江苏 镇江 212013)

水泥基材料作为一种建筑材料，目前在房屋建筑、公路桥梁、隧道涵洞及河堤大坝等工程结构领域有着广泛应用[1-2]。但普通水泥基材料存在抗拉强度低、韧性差、易开裂等缺陷，易导致结构出现性能劣化和耐久性降低的问题。为解决上述问题，20世纪90年代，美国密歇根大学Li等[3-4]通过在水泥基体中加入纤维，成功设计出具有应变硬化特性、良好的延展性、抗裂性及抗冲击韧性等优点的高性能材料，并称之为工程用水泥基复合材料（ECC）。此后，通过在基体中掺入各种类型的纤维改善水泥基材料的抗裂性和耐久性逐渐成为获得高性能水泥基材料的有效途径[5-6]。目前，常用于水泥基增强的纤维材料主要有钢纤维、聚丙烯纤维、聚乙烯醇（PVA）纤维和耐碱玻璃纤维等，这些纤维增强材料均在水泥基材料增强中发挥了重要作用，各有特点，但也存在一些不足，如：钢纤维易腐蚀，聚丙烯纤维弹模偏低，PVA纤维价格昂贵等。相比之下，耐碱玻璃纤维在受力性能、经济性及耐久性等综合方面表现出较优的特点[7]，采用其进行水泥基材料增强可取得较好的效果[8-9]，因此备受关注。而纤维增强水泥基材料的受压本构关系是其宏观受力性能的综合反映，是进行构件设计和结构非线性分析的基础，且不同纤维增强水泥基材料的本构关系由于纤维特性和掺量不同也会存在一定差异。因此，要明确耐碱玻璃纤维增强水泥基材料（简称耐碱玻璃纤维ECC）的力学性能，有必要对其受压特性及本构关系展开深入研究。

关于耐碱玻璃纤维ECC的受力特性，国内外学者从不同角度开展了相关研究。Tassew[10]、Kizilkanat[11]及程从密[12]等分别从不同角度对耐碱玻璃纤维增强水泥基材料的力学性能进行研究，结果表明，耐碱玻璃纤维可以明显改善水泥基体的抗裂能力，同时也能提高水泥基材料的抗压、抗折和变形性能。张王田等[13]为制备高性能和长寿命的耐碱玻璃纤维ECC，采用多因素设计方法，确定了水胶比与纤维体积掺量的较优范围。耐碱玻璃纤维还可作为连续长纤维用于水泥基材料性能增强，如：关于碳-玻纤维织物网增强混凝土（TRC）材料的相关研究目前很多，主要涉及TRC材料的拉伸、弯曲力学性能及相关加固应用等[14-18]。近年来，还有学者通过在TRC基体中掺入短切耐碱玻璃纤维形成高延性TRC（即纤维网增强ECC），以进一步改善TRC基体易开裂和韧性差等缺点[19-21]。在纤维增强水泥基材料受压本构关系方面，目前的研究主要针对PVA纤维增强水泥基复合材料，如：Zhou[22]、李可[23]、李艳[24]及Xu[25]等通过单轴压缩试验研究，分别提出关于PVA纤维增强水泥基复合材料的受压应力-应变关系全曲线模型；闫维明等[26]研究了钢-聚丙烯和PVA-聚丙烯两类混杂纤维水泥基复合材料的应力-应变曲线方程。综上，关于耐碱玻璃纤维ECC本构关系研究的相关报道尚少，不利于耐碱玻璃纤维ECC及以此为基体的高延性TRC材料的进一步推广应用。

因此，本文通过对不同设计参数的耐碱玻璃纤维ECC试件进行轴压性能试验，结合试验和理论分析，详细探讨不同纤维掺量、纤维长度及水灰比对耐碱玻璃纤维ECC受压应力-应变关系的影响，并基于试验结果建立包含上述参数影响的受压应力-应变本构关系模型，为耐碱玻璃纤维ECC在结构或构件的受力分析及量化设计提供理论基础。

1 试验概况

1.1 试验设计

试验共制作30组试件研究耐碱玻璃纤维ECC的受压应力-应变关系，每组制作3块40 mm×40 mm×160 mm的试件进行棱柱体轴心抗压性能试验。设计的水灰比为0.32、0.36、0.40；基于文献[16,21]的研究结果，纤维长度较大（>10 mm）时，水泥基体的增强增韧效应相对较好，故本文主要采用纤维长度为12和18 mm两种耐碱玻璃纤维；当纤维掺量较大（>8%）时，砂浆基体流动性变得较差，成型比较困难，振捣过程中也会导致大量气泡无法振捣出，进而影响耐碱玻璃纤维ECC性能，故将短切耐碱玻璃纤维最大质量掺量设计为8%，最终设计纤维掺量为5种，分别为1.0%、3.0%、5.0%、6.5%及8.0%。试验还制作了3组仅考虑水灰比的普通水泥基试件，以与耐碱玻璃纤维ECC试件作对比，每个工况试件均制作3块。需要说明的是，上述纤维掺量为对应于水泥的质量掺量Mf，该掺量可根据配合比转化为体积掺量Vf，相关换算方法参见文献[21]。

1.2 试验材料

配制高性能水泥基的原材料主要包括普通硅酸盐水泥（P·O 42.5）、普通河砂（中粗砂）、JM-PCA（Ⅰ）型聚羧酸减水剂、耐碱玻璃纤维（12、18 mm）和自来水。耐碱玻璃纤维的密度为2.7 g/cm3，抗拉强度为2 500～3 500 MPa，弹性模量为80.4 GPa，纤维丝直径为15 µm。水泥基材料的配比见表1。

表1 耐碱玻璃纤维ECC配合比Tab. 1 Ratio of alkali-resistant glass fiber ECC

1.3 试验装置及加载

试件成型养护28 d后在60 t材料拉压力试验机进行单轴受压试验，试件受压面为40 mm×40 mm。试验采用位移加载，加载速率设定为0.2 mm/min；每次加载前先进行两次预加载，以消除试验装置加载前存在的空隙。试验采用东华测试的应变仪采集系统自动采集应变，单轴受压试验加载装置如图1所示。

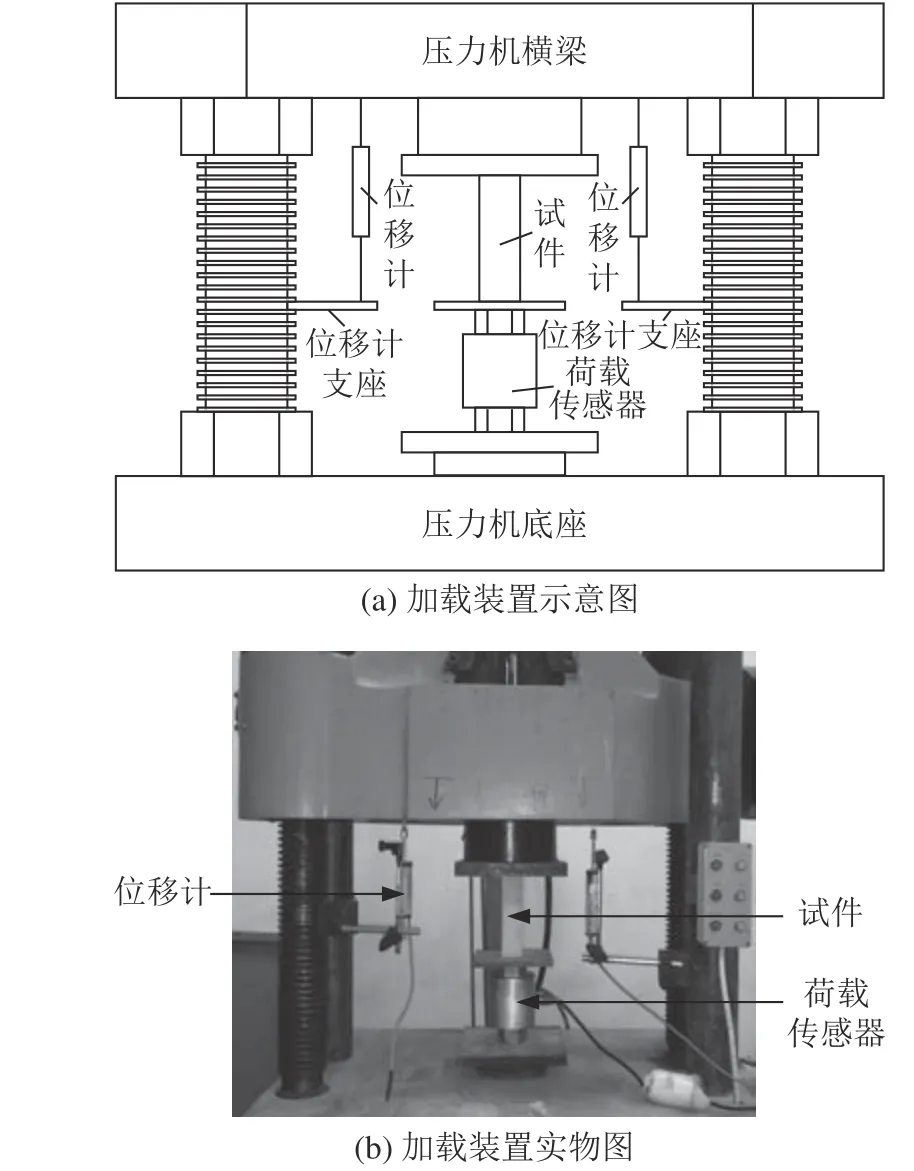
图1 单轴受压试验装置Fig. 1 Experimental set up for axial compression test

2 试验结果及分析

2.1 试验现象与破坏形态

试验初期，随着荷载缓慢增加，试件表面并无明显变化。达到最大承载力后，试件中间偏上部分逐渐出现细小的裂纹，承载力开始下降，但由于试件中耐碱玻璃纤维的存在，使其在试件出现较小裂缝时仍具有较大的抗压强度。随着位移继续增加，裂缝持续扩大，可听到细小的玻璃纤维丝断裂的声音，试件周围裂缝处有小碎块剥落；达到一定的位移值后，承载力下降速度加快，最终试件被压溃。从试件的裂缝中可以观察到，断裂面有众多细小的玻璃纤维丝存在，部分未被拉断的玻璃纤维丝仍在连接，破坏后的试件裂而不散，仍能保持一个整体。对比组试件达到最大承载力后，侧面出现明显裂缝，且裂缝迅速扩大，试件直接被压溃，并发出巨大的响声，无法形成整体。对比组试件破坏速度明显，破坏前无明显征兆，属于典型的脆性破坏。耐碱玻璃纤维增强ECC试件与对比试件的破坏形态如图2所示。

图2 水泥基材料受压破坏形态Fig. 2 Failure modes of cement-based materials under compression

由图2可知，随着玻璃纤维掺量增加，试件破坏时的裂缝由一条较宽主裂缝逐渐转成多条交叉细小的裂缝。试验现象表明，在水泥基材料中加入耐碱玻璃纤维可有效增强水泥基的韧性，改善水泥基的脆性。耐碱玻璃纤维对于水泥基材料的增强增韧机理，主要体现在对水泥基材料宏观裂缝抑制和内部结构桥联方面，其微观结构组成可参见文献[27]。

2.2 抗压强度

耐碱玻璃纤维ECC受压试验结果见表2。

表2 耐碱玻璃纤维ECC受压试验结果Tab. 2 Compression test results of alkali-resistant glass fiber ECC

由表2可知：加入耐碱玻璃纤维后，其抗压强度会有不同程度提升，试件的抗压强度提升程度（即增强比）大致呈现先上升后下降的趋势。水灰比为0.32、纤维长度为12 mm的纤维增强ECC试件，纤维掺量分别为1.0%、3.0%、5.0%、6.5%和8.0%时的抗压强度较未增强的对比试件（S0.32-0-0）分别提升13.4%、23.6%、24.8%、26.8%和23.0%；相同水灰比下，纤维长度为18 mm的纤维增强ECC试件，纤维掺量分别为1.0%、3.0%、5.0%、6.5%和8.0%时，其抗压强度较对比试件分别提升11.8%、25.8%、28.7%、25.6%和14.2%。总的来说，纤维长度增加，ECC试件的抗压强度略有增加但幅度不大，与对比试件相比，抗压强度最大提升幅度约30%；同时，纤维掺量对ECC试件的抗压强度也存在明显的影响，质量掺量为5.0%和6.5%时，试件的抗压强度提升效果最明显。

水灰比对试件抗压强度也有较大影响，在相同纤维长度和掺量条件下，增加水灰比会降低试件的抗压强度。如：纤维长度为12 mm、掺入量为1.0%的纤维增强ECC试件，当水灰比分别为0.32、0.36、0.40时，试件的抗压强度分别为55.8、44.3和37.4 MPa，呈明显的下降趋势。

2.3 受压应力-应变曲线

为说明耐碱玻璃纤维对水泥基受压应力-应变关系的影响，图3、4为不同水灰比、纤维长度和掺量的耐碱玻璃纤维ECC试件与普通水泥基试件的受压应力-应变关系对比结果。

由图3、4可以看出：普通水泥基试件经历了弹性上升阶段后很快进入下降段，呈现出明显的脆性破坏特征。耐碱玻璃纤维ECC试件基本上均经历了弹性上升、塑性强化和线性下降3个阶段，且其塑性变形能力均优于普通混凝土；其峰值应变在0.004左右，明显大于普通水泥基材料的应变0.002；其最大应变值均在0.005 5左右。 掺入适量耐碱玻璃纤维可以提高材料的抗压强度、延性和韧性，但掺入量过高反而会使抗压强度和延性降低。

由图3、4还可以看出：当纤维掺量从0增加至6.5%左右时，试件的抗压强度和变形性能随纤维掺量增加而增加；但掺量超过6.5%增加到8%时，增加纤维掺量反而会降低试件的抗压强度和变形能力。此外，试件的弹性模量与水灰比、纤维掺量及长度也存在一定的关系，当水灰比为0.32～0.36、纤维质量掺量为0～8.0%时，弹性模量在22 000～30 000 MPa范围内浮动。

需要指出的是，图3、4中耐碱玻璃纤维增强ECC的受压应力-应变曲线下降段并不完整，由于后半段试件发生骤然破坏，导致仪器无法测出其应力与应变的变化过程。

图3 纤维长为12 mm增强试件的受压应力-应变曲线Fig. 3 Compressive stress-strain curves of the fiber reinforced specimen with the fiber length of 12 mm

图5为各试件的极限强度fuu与峰值强度fcu比值的统计关系。由图5可知，极限强度和峰值强度的比值集中在0.55附近。因此，本文取峰值强度后对应于0.55倍峰值强度的变形为极限变形。

图4 纤维长18 mm增强试件的受压应力-应变曲线Fig. 4 Compressive stress-strain curves of the fiber reinforced specimen with the fiber length of 18 mm

图5 极限强度和峰值强度的比值的变化趋势Fig. 5 Trend of the ratio of ultimate strength to peak strength

2.4 影响因素对比分析

2.4.1 水灰比

图6为耐碱玻璃纤维ECC试件的受压应力-应变曲线随水灰比变化趋势。

图6 纤维增强试件的受压应力-应变曲线随水灰比变化Fig. 6 Compressive stress-strain curves of fiber reinforced specimens varies with the water-cement ratio

由表2及图6可知，随着水灰比的增加，试件的抗压强度呈现出明显的下降趋势，但水灰比对变形的影响不明显。以纤维长度12 mm，纤维掺量5%为例，当水灰比分别为0.32、0.36、0.40时，试件抗压强度分别为61.4、52.5、42.2 MPa。相较于水灰比为0.32的试件，水灰比为0.36和0.40试件的抗压强度分别下降了8.9、19.2 MPa。从抗压强度增强比来看，水灰比越大，纤维增强效果越明显。以纤维长度18 mm为例：水灰比为0.32时，不同纤维掺量试件的抗压强度增强比的平均值为21.2%；水灰比为0.36时，不同纤维掺量试件的抗压强度增强比的平均值为26.5%；水灰比为0.40时，不同纤维掺量试件的抗压强度增强比的平均值为27.9%。不同水灰比各组试件的抗压强度增强比的最大值分别可达到28.7%、39.3%、44.0%。但总体比较，水灰比为0.32时试件的抗压强度较高。因此，考虑到水泥基材料的力学性能，水灰比应控制在0.32时为宜。

2.4.2 纤维长度

由受压试验结果（表2）可以看出，增加纤维的长度可以提高增强试件的变形能力，提升增强试件的抗压强度，但是提升效果不明显。如图7所示，分别选取3种水灰比（分别为0.32、0.36及0.40）下两种纤维掺量（3.0%和6.5%）的增强试件对其受压应力-应变曲线进行对比分析，以说明12和18 mm纤维长度对试件的变形能力和抗压强度的影响。

由图7可知，纤维长度对试件变形性能有一定的影响，相对于掺入长12 mm纤维的水泥基体，掺入长18 mm纤维的水泥基体具有更好的变形性能，且在达到峰值应力后，掺入18 mm纤维的水泥基体的荷载下降速度较慢。可见，纤维长度增加可以使纤维在水泥基材料中发挥更好的作用，力学性能增强效果越明显，故在选择水泥基增强材料时应优先选择长度较大的纤维。

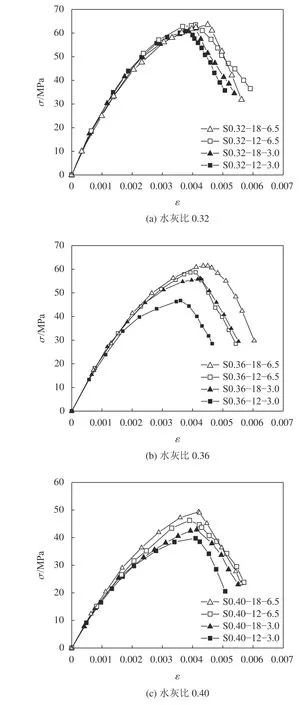
图7 不同纤维长度的受压应力-应变曲线对比Fig. 7 Compressive stress-strain curves of different fiber lengths

2.4.3 纤维掺量

由耐碱玻璃纤维ECC受压试验结果（表2）可以看出，纤维掺量对水泥基材料的抗压强度提升明显。随着纤维掺量的提升，水泥基材料的抗压强度呈现先增加后减小的趋势；在纤维掺量为6.5%时，提升的效果最高，可以达到44.0%；随着纤维掺量的继续增加，荷载反而略有下降。

结合图3和4可以看出，耐碱玻璃纤维ECC与普通的水泥基材料相比，无论是抗压强度还是应变均有较大的提升，而且普通水泥基材料达到最大应力后立即破坏，表现出来明显的脆性破坏，而耐碱玻璃纤维ECC纤维的掺量越高，在达到峰值荷载后表现出的延性越好。

3 受压应力-应变曲线模型

3.1 模型概述

耐碱玻璃纤维ECC的受压应力-应变曲线反映了其最基本的力学性能，是研究其结构和受力性能的最主要依据。因此，需要通过对耐碱玻璃纤维ECC实测的受压应力-应变曲线进行分析，以建立相应的数学模型。根据本文试验结果，耐碱玻璃纤维ECC的受压应力-应变曲线主要包括上升段和下降段两部分，可分别采用2次抛物线和斜直线形式进行描述，如图8所示。

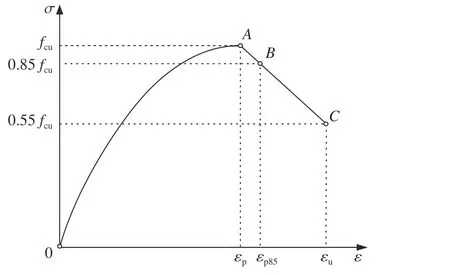
图8 耐碱玻璃纤维ECC复材受压应力-应变曲线模型Fig. 8 Stress-strain curve model of alkali-resistant glass fiber ECC under compression

3.2 峰值应力及应变确定

对于式（1）的受压应力-应变曲线计算模型，还应确定不同因素影响下耐碱玻璃纤维ECC峰值应力和应变。

1）峰值应力

根据本文的试验结果，耐碱玻璃纤维ECC峰值应力的可采用式（2）计算：

式中：fcu0为普通水泥基材料的峰值应力；C为水灰比；λf为纤维掺量的特征值，定义为纤维的体积掺量Vf与纤维长度lf的乘积与纤维直径df的比值，体积掺量Vf可以通过配合比和纤维的质量掺量Mf求得，纤维长度lf的单位为m； α1、 α2分别为纤维掺量特征值对水泥基材料的影响系数，通过对峰值应力试验结果拟合（图9），得到 α1、 α2分别为-0.027、0.892。由图9可知，模型计算值与试验值吻合效果较好。

图9 不同参数下耐碱玻璃纤维ECC峰值应力计算值与试验值比较Fig. 9 Comparison of calculated and tested peak stress values of alkali-resistant glass fiber ECC under different parameters

2）峰值应变εp

纤维掺量和长度对耐碱玻璃纤维ECC峰值应变有较大的影响，随着纤维掺量和长度的增加，耐碱玻璃纤维ECC峰值应变也随之增加；水灰比对于耐碱玻璃纤维ECC峰值应变影响较小。故主要考虑纤维掺量和长度的影响，提出计算公式如下：

式中： εp为 耐碱玻璃纤维ECC峰值应变； ε0为普通水泥基材料峰值应变；Vf为纤维的体积掺量；lf为纤维长度； β1、 β2为纤维的体积掺量和纤维长度对耐碱玻璃纤维ECC峰值应变的影响系数，通过对峰值应变试验结果进行拟合（图10），得到 β1、 β2分别为12.035、32.725。如图10所示，模型计算结果与试验值吻合较好。

图10 不同参数下耐碱玻璃纤维ECC峰值应变计算值与试验值比较Fig. 10 Comparison of calculated and tested peak strain values of alkali-resistant glass fiber ECC under different parameters

3.3 85%峰值点对应的应力及应变

85%峰值点对应的应力即为0.85倍峰值应力，其应变通过可以通过图11给出的耐碱玻璃纤维ECC试件的受压峰值应变和85%峰值点对应应变的关系确定。

由图11可知，两者呈线性关系，其计算公式表达如式（4）所示：

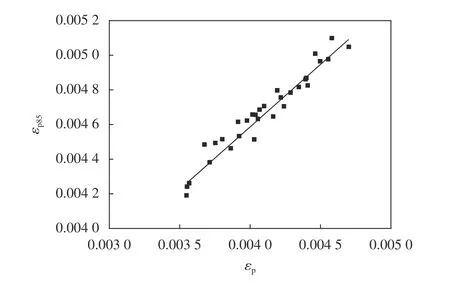
图 11 εp-εp85关系Fig. 11 Relationship ofεp-εp85

综上，确定了耐碱玻璃纤维ECC受压应力-应变曲线的峰值点和85%峰值点，还需确定极限点即可得到完整的受压应力-应变计算模型。根据图5中各试件的极限强度与峰值强度的关系，其极限点可取0.55倍峰值应力对应的点。

3.4 计算曲线与试验曲线比较

为验证本文模型的合理性，图12给出了本文计算模型和Zhou[22]、李艳[24]及闫维明[26]等所提的PVA纤维ECC受压应力-应变关系模型应用于本文耐碱玻璃纤维ECC试件的受压应力-应变曲线计算结果与试验结果的比较。由图12可知：在本文模型计算结果曲线的上升段，模型计算值与试验值基本重合；在下降段两者也能基本保持吻合。这表明本文所提模型可用于描述耐碱玻璃纤维ECC受压应力-应变关系曲线。需要说明的是，经验模型的准确性有赖于试验数据的量值，通常数据越多，所建立模型的适用性越好。因此，本文所提模型（即式（1）～（4））主要适用于模型参数（如水灰比、纤维掺量及长度）与本文试验参数相类似的耐碱玻璃纤维ECC受压应力-应变关系的预测。此外，Zhou等[22]的模型的计算结果与试验结果相比，整体吻合性欠佳；李艳[24]的模型计算值在曲线上升段低于试验结果，而在曲线下降段又高于试验结果；闫维明等[26]的模型在上升段计算值能与试验值吻合较好，但在下降段却高估了ECC的应力。由此可见，将基于PVA纤维ECC受压试验结果建立的受压应力-应变关系模型用于描述耐碱玻璃纤维ECC的受压应力-应变关系会存在较大的偏差，这与采用不同纤维增强水泥基材料所得复合材料的特性存在差异相关。这进一步表明，本文建立的适用于耐碱玻璃纤维ECC受压应力-应变关系预测的模型有其必要性。

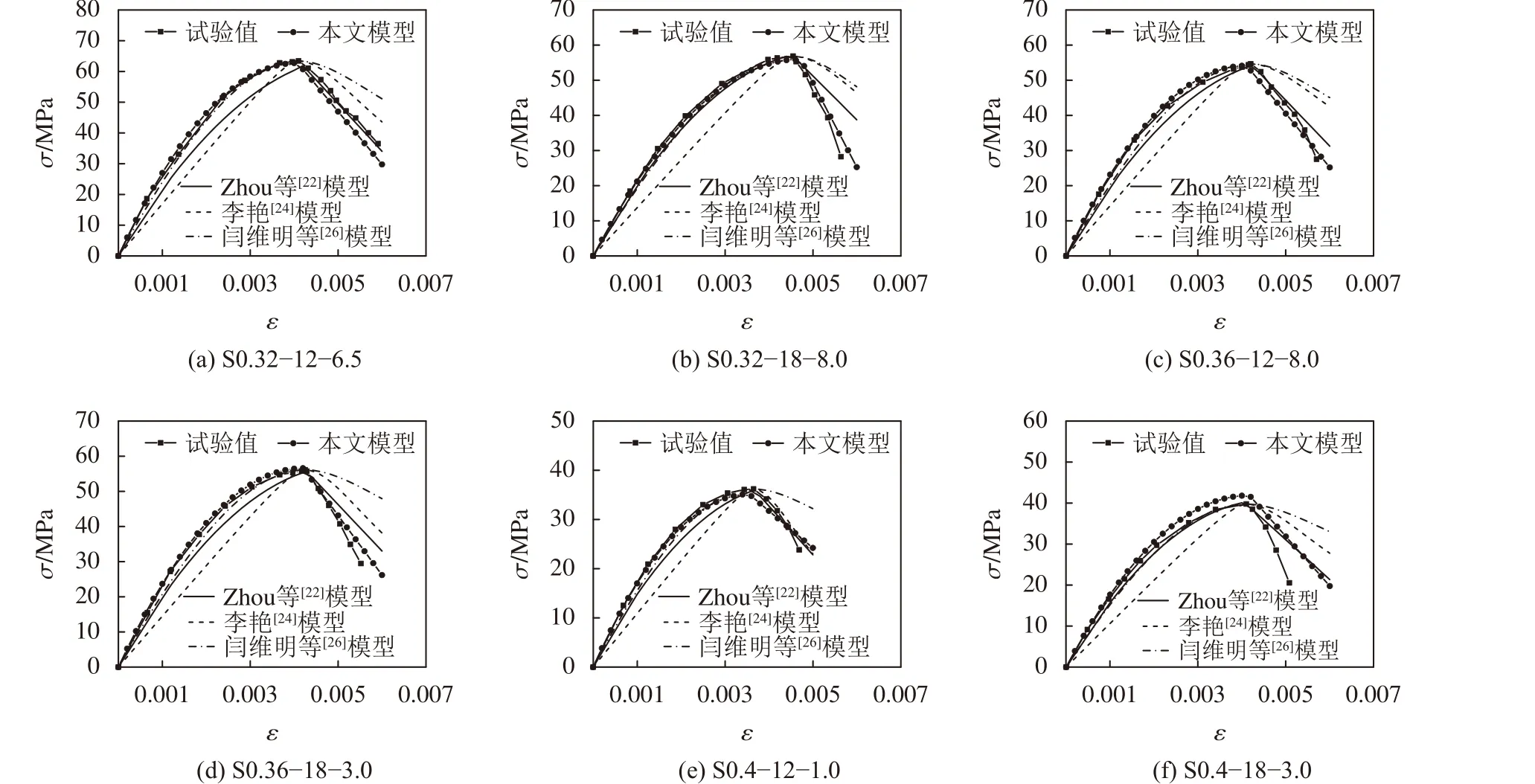
图12 各模型受压应力-应变曲线计算结果与试验结果的对比Fig. 12 Comparison of calculated results of compression stress-strain curve of each model and experimental results

4 结 论

1）在水泥基材料中加入耐碱玻璃纤维可以明显改善水泥基材料单轴受压状态下基体的抗裂性能、抗压强度和变形能力。相较于普通水泥基材料的抗压强度和变形能力，最大可分别提升44.0%和117.6%。试件纤维长度主要影响其变形性能，纤维长度越长，其变形性能越好。此外，随着纤维掺量的增加，其变形性能增加，其抗压强度先增加后略有降低。

2）水灰比主要影响耐碱玻璃纤维ECC的抗压强度，增加水灰比会降低试件的抗压强度。当水灰比增加时，试件的抗压强度下降程度增加；同时，增加纤维长度和纤维掺量可降低抗压强度的下降程度。总体上看，水灰比为0.32，纤维长度为18 mm，纤维质量掺量为6.5%的耐碱玻璃纤维ECC能取得较好的综合力学性能。

3）耐碱玻璃纤维ECC受压应力-应变曲线可以分为上升段和下降段两个部分，可分别采用2次抛物线和直线进行描述；本文提出的耐碱玻璃纤维ECC受压应力-应变曲线模型中考虑了水灰比、纤维长度和纤维掺量的影响，模型的计算结果与试验结果吻合较好，可用于描述耐碱玻璃纤维增强水泥基材料的受压全过程性能。