基于曲面响应分析的混流式多级泵优化设计

2022-10-13郭勇胜袁寿其杨海龙王彪彪司乔瑞

流体机械 2022年8期

郭勇胜，王鹏，袁寿其，杨海龙，王彪彪，司乔瑞

（1.江苏大学流体机械工程技术研究中心，江苏镇江 212013；2.重庆水泵厂有限责任公司，重庆 400033）

0 引言

混流式多级泵综合了离心泵和轴流泵的优点，广泛应用于电站、石油化工、城市供水等领域，具备良好的应用前景。随着计算机技术的发展，流体机械数值预测用于其性能的优化也越来越普遍。正交试验法作为一种试验设计因其经济、快速的特点被广泛应用于水泵的优化［1-3］。李彦军等［4］基于正交试验对高扬程混流泵进行了优化，发现叶轮叶片出口安放角对扬程影响最大，叶片保角对效率影响最大。当前很多学者采用响应面模型、人工神经网络等构建优化目标和设计参数的近似函数关系，进而通过优化算法寻优求解［5-9］。杨敬江等［10］基于Isight平台结合NSGA-Ⅱ优化算法对混流泵优化，使其效率扬程均有提高。王延锋等［11］基于GA-BP神经网络对多级泵水力性能优化，扬程效率提高且高效区变宽。

相对上述优化方法，曲面响应法可以将多参数函数关系通过图像形式显示出来，直观的判别优化区域，与正交试验法相比寻优效果更好，也比智能算法优化节省时间，在泵的优化预测领域具有广泛的应用前景［12-14］。ALAWADHI等［12］采用遗传算法和曲面响应对离心泵优化设计，选取了6个参数作为设计变量，研究结果表明：外壳上局部压力和应力最大波动对应于套管0°～30°相位角，而该相位角对应于该区域最大侵蚀速率。ABDELLAH等［14］通过曲面响应确定了外啮合齿轮泵入口直径为15 mm，转速为3 500 r/min时的最佳设计点。多级泵由于参数因素较多，为提高其设计点的效率，通常以单级优化为基础进行优化。魏江等［15］利用曲面响应法构建了卧式多级离心泵首级设计工况点效率与叶轮设计变量之间的近似函数，分析了单个参数的影响，找到在设计工况点将效率提高3.62%的最佳参数组合，并且在高流速条件下改善了内部流动。陶然等［16］通过对轴流泵内部流场的优化，使叶片吸力面与压力面之间的压差增大，泵内水力损失减小，扬程和效率都有明显提高，高效区明显扩大。

目前国内外学者对于轴流泵和多级离心泵的优化设计以及内流分析已进行了大量的研究，但鲜有混流式多级泵的相关研究。本文以混流式多级泵为研究对象，基于曲面响应法对多级泵首级进行优化设计，选取四个参数共设计31组方案，并拟合扬程效率回归方程，得到最优组合。最后进行多个流量工况下五级泵数值预测，并进行试验验证。

1 优化模型及优化方法

1.1 控制方程

泵内介质视为三维黏性、不可压缩的非定常流动，在对该模型进行CFD（Computational Fluid Dynamics）计算时，质量和动量守恒控制方程为：

式中 ρ——密度；

t——时间；

ui，uj——i，j方向的雷诺平均速度；

p——平均静压；

fi——重力加速度分量；

u′i，u′j——i，j方向的速度脉动量。

1.2 混流式多级泵三维建模

模型泵共有5级，其关键水力参数见表1。该泵采用环形吸水室进口，进口管垂直泵轴。

表1 多级泵叶片参数Tab.1 Blade parameters of multistage pump

基于UG软件对各个流体域进行三维建模，图1示出将流体域模型简化为进水段、环形吸水室、叶轮、间隙、空间导叶和出水段六部分。计算时，环形吸水室可实现水均匀地从四周涌入叶轮，进水段和出水段分别进行了适当延长以保证流动的充分发展，优化过程中对泵叶轮的几何参数的优化效果采用单级泵进行评估。

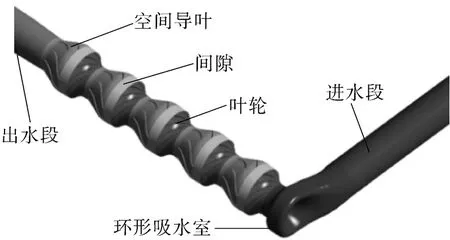
图1 混流式多级泵计算域Fig.1 Calculation domain of mixed flow multistage pump

1.3 计算域网格划分

采用Ansys ICEM对计算域进行网格划分。本文的叶轮、导叶、进出口延长段网格划分采用六面体结构化网格，环型吸水室采用非结构化网格，部分网格细节如图2所示。

图2 部分网格划分示意Fig.2 Schematic diagram of mesh generation

1.4 网格无关性分析

对5套不同网格数量的单级混流泵模型进行设计工况下的定常数值计算，获得扬程的波动变化曲线，如图3所示。可以看出计算网格数大于268万以后扬程的波动值控制在2%以内，故选取网格数为268万作为优化设计过程中单级模型泵的网格参照。

图3 网格无关性Fig.3 Grid independence

1.5 边界条件设置

模型泵流场数值计算和性能预估在Ansys CFX中进行。选择标准k-ε湍流模型控制方程，设置进口直管、间隙、导叶、出口等计算域为静止域，设置叶轮计算域为旋转域。叶轮与环形进口、叶轮与导叶之间交界面设置动静交界面，网格连接方式为GGI。工作介质设置为25 ℃的清水，进口边界设置1.01×105Pa总压进口，出口边界条件选择质量流量出口。湍流强度设为5%，所有壁面均采用无滑移壁面，壁面粗糙度设为0.012 mm。

2 全因子试验和响应面试验设计

2.1 全因子试验各变量组合及计算结果

对原型泵的优化分为2个阶段：线性试验（全因子试验）和二次试验（响应面试验）。

参考初始方案设计参数，提出参与试验的叶轮参数的取值范围如下：叶轮叶片前盖板流线进口安放角A（13°，26°）、中间流线进口安放角B（24°，38°）、后盖板流线进口安放角 C（40°，52°）以及叶片出口安放角D（20°，35°）。全因子试验采用4因素2水平参数表（表2）进行各变量的组合，并增设3组中心点试验以验证随机误差。各方案数值计算结果见表3。

表2 参数表（4因素2水平）Tab.2 Table of parameters (4 factors, 2 levels)

表3 4因素2水平的计算结果Tab.3 Calculation results of 4 factors and 2 levels

2.2 全因子试验方差分析

对效率进行方差分析，分析结果见表4。方差分析中的P值（主效应0.078、2阶交互项0.845）均大于0.05，则表明该效率模型总的来说无效。弯曲项P值为0.007＜0.050，存在弯曲。失拟项的P值为0.461＞0.050，不存在失拟。

表4 全因子计算效率方差分析Tab.4 Variance analysis of efficiency calculation of full factors

表5示出扬程方差分析中存在P值（主效应0.000、2阶交互项0.545）小于0.05，则表明该扬程模型总的来说有效的。弯曲项P值为0.129＞0.050，不存在弯曲。失拟项的P值为0.341＞0.050，模型不存在失拟。但对同一组试验数据进行扬程方差分析和效率方差分析时，需两者同时满足模型有效、不存在弯曲、不存在失拟才有意义。整体来说，全因子试验效率方差分析中，线性回归方程结果失真，说明必然存在二次项及以上因子的影响，需要进一步进行设计试验。

表5 全因子计算扬程方差分析Tab.5 Variance analysis of head calculation of full factors

2.3 曲面响应优化设计

二次试验选用曲面响应中的中心复合设计法。曲面响应设计是在全因子试验设计分析中发现有弯曲现象后再增补的一些实验点分析的设计，曲面响应的试验点由立方体点、中心点以及星号点3部分构成，其中立方体点由全因子试验完成，对应的方案数为kn，其中k为试验因子数，n为每个试验因子的水平数。在k个因子数的情况下，星号点的方案数为2k。

曲面响应方案数及其各方案的计算结果见表6。本次试验是在全因子试验的基础上进行的优化设计，立方体点的方案数为42=16，星号点对应的方案数为2×4=8，为了能在整个试验区域内预测值具有一致均匀精度，选取的中心点重复方案数为7，共计方案数为16+8+7=31。

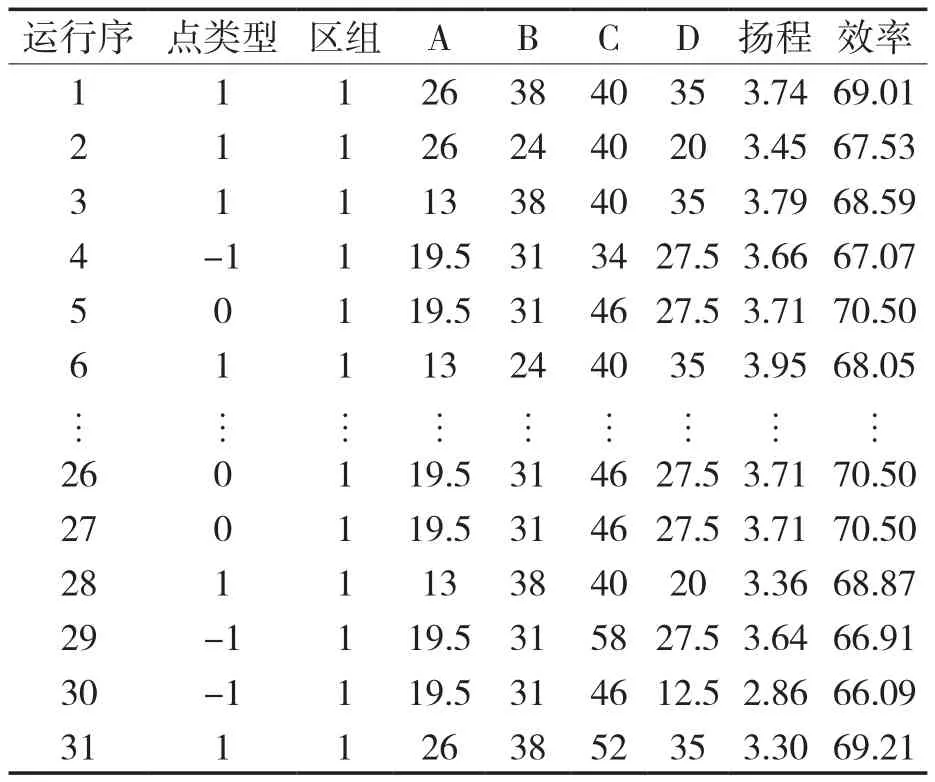
表6 曲面响应方案数及其计算结果Tab.6 Number of surface response schemes and their calculation results

2.4 曲面响应方差分析

将曲面响应效率计算结果进行方差分析，结果见表7，P值（主效应0.023、平方项2阶0、交互项0.905）的主效应和平方项均小于0.05，表明该效率模型有效。效率方差分析中的失拟项P值为0.288，大于0.05，表明该模型不存在失拟。

表7 曲面响应计算效率方差分析Tab.7 Variance analysis of efficiency calculation of curved surface response

将曲面响应扬程计算结果进行方差分析，结果见表8，P值（主效应0.000、平方项2阶0.013、交互项0.417）主效应和平方项均小于0.05，则表明该扬程模型有效。扬程方差分析中的失拟项的P值为0.321＞0.050，这表明该模型不存在失拟。扬程方差分析跟效率方差分析同时满足模型有效、不存在失拟这一条件，故而可用于后续分析。

表8 基于曲面响应计算的扬程方差分析Tab.8 Variance analysis of head based on surface response calculation

2.5 拟合回归方程以及回归方程求解

表7，8的方差分析中各项的P值表示各项效应的显著性，各项的P值越接近0，表示对回归方程的影响越显著，P值大于0.05，可认为该项为弱显著影响因子，可在后续数据处理中删除以突出强显著因子对回归方程的贡献。表7中单因子对效率的影响顺序为D（0.012）＞B（0.061）＞A（0.133）＞C（0.448），其中B、D为强显著因子，A，C为弱显著因子，但单因子是构成平方项的主要项，不能直接删除。平方项B2（0.001）=C2（0.001）=D2（0.001）＞ A2（0.012）均小于 0.05且较为接近0，为强显著因子。2因子交互项中P值均大于0.05为弱显著因子，在后续分析中删除。表8中单因子对扬程的影响顺序为D（0.000）=B（0.000）＞ A（0.101）＞ C（0.151），其中 B、D 为强显著因子，A，C为弱显著因子，同理单因子不能删除。删除弱显著因子后得到效率回归方程为：

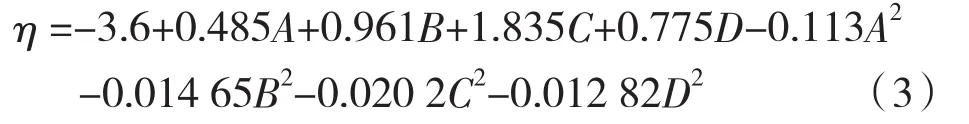
为了使效率和扬程回归方程中具有相同的影响因子，故而在扬程回归方程拟合过程中删除效率方差分析中的弱显著因子，得到扬程回归方程为：

得到效率回归方程后，对效率回归方程求解各变量的偏导数，使其偏导数为0，得到方程驻点所对应的因变量值，外加因变量取值范围的极值点，进而可在所给定的因变量范围求解出最大值。图4示出各因变量最优组合取值及其自变量的最大值求解。（A，B，C，D）的最优组合为（21.469 7°、32.333 838 4°、45.393 9°、30.075 8°），效率的最大值为70.734 8%。将相应变量的最优组合带入扬程回归方程，得扬程为3.76 m。

图4 响应优化器求解结果Fig.4 Solution result of response optimizer

2.6 响应面分析

图5示出在效率最大值点时有15°＜A＜30°，25°＜B＜37°，40°＜C＜50°，25°＜D＜35°。初始设置响应变量的范围时，最大值点的因变量均在所设置响应变量的范围内，不存在将最大值点遗漏而求解结果是极大值点的情况，故而本次试验设计所求效率的计算结果即为本次试验所求效率的最大值。

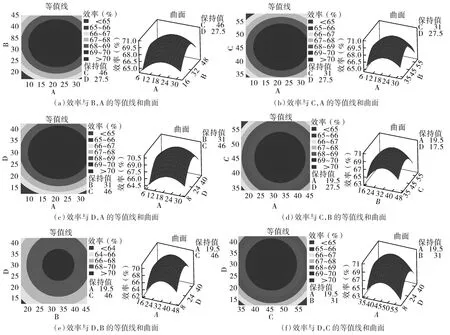
图5 效率与变量交互项的等值线和曲面Fig.5 Contour map and surface map of the interaction between efficiency and variables

3 方案对比及分析验证

3.1 优化方案对比

优化方案中CFD计算均采用定常结果。图6示出单级泵优化前后性能的对比，由图可知优化方案与初始方案相比，在设计工况点扬程不变的情况下其效率提高了5.09%。

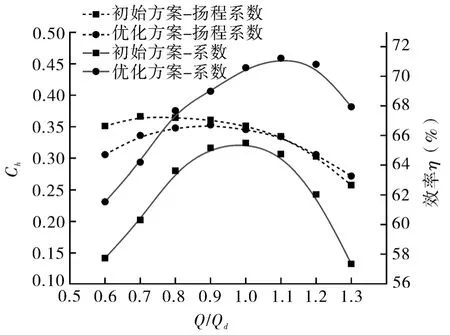
图6 优化前后外特性对比Fig.6 Comparison of pump external characteristics before and after optimization

图中无量纲流量系数和扬程系数定义为：

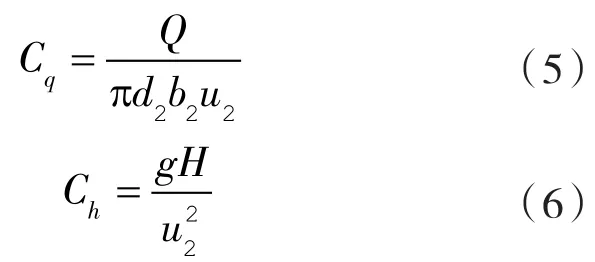
由于该模型泵的各级导叶叶轮均相同，将单级和五级泵模型数值外特性对比，如图7所示。

图7 单级泵和五级泵外特性对比Fig.7 Comparison of external characteristics between singlestage pump and five-stage pump

由图可知，两者效率特性曲线近似平行，扬程特性曲线在0.8Qd～1.2Qd范围内基本一致，说明以混流式多级泵效率为优化目标时采用单级叶轮优化为基础实现多级泵的整体优化设计是可行的。

3.2 优化方案内流分析

对优化前后计算域内流场分析，可以更直观地分析泵的工作情况。图8示出设计点工况优化前后叶轮表面静压对比。从图中可以看出优化前叶片进口前盖板附近低压区较大，结合图6可知泵效率随流量的增大急剧下降，说明在大流量工况下运行时，叶片出口相对液流角大于叶片安放角，在叶片工作面发生了脱流现象，严重影响叶片工作面做功，导致效率降低。优化后叶片进口前盖板附近低压急剧减小，主要集中分布在叶片背面进口的狭小区域，叶轮表面压力从叶片进口到叶片出口变化更均匀，叶轮叶片型线更加合理，优化后效率提升明显。