降雨入渗过程中土坝边坡稳定性的概率分析

修冬红

(河北省水利水电勘测设计研究院集团有限公司，河北 石家庄 050000)

1 分析方法

本文利用饱和-非饱和渗流理论计算了降雨入坝的渗流场，然后用概率分析方法对其稳定性进行了分析。根据输入参数的平均值，本文采用极限平衡法确定临界滑动面。然后考虑输入参数的可变性，利用蒙特卡罗方法对临界滑动面进行概率分析，最后计算坝坡的不稳定概率[1-7]。

1.1 降雨入渗引起的瞬态渗流分析

本文利用渗流分析软件SEEP/W[8]研究坝坡的瞬态渗流和湿润锋推进。饱和-非饱和土壤中的渗流受达西定律影响。非饱和土壤的渗透系数不是常数，而是饱和度或土壤吸力的函数。水流通过土壤的一般二维控制微分方程如式(1)：

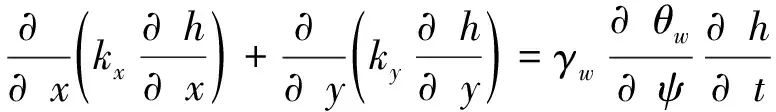
(1)

式中：kx和ky为x方向和y方向的渗透率系数，m/d；γw为水的单位重量，N/m3；θw为体积含水量，%；ψ为土壤吸力，kPa；t为时间，d。

根据该方程，在进行瞬态渗流分析时，必须已知土壤水分特征曲线，即体积含水量和土壤吸力之间的关系，以及渗透函数。

1.2 非饱和土的抗剪强度

采用极限平衡法进行边坡稳定性分析的软件SLOPE/W可用于评估降雨入渗期间坝坡的稳定性，包括不稳定概率。非饱和土壤的抗剪强度由扩展莫尔-库仑破坏准则描述如式(2)：

τf=c′+(σn-ua)ftanφ′+(σa-uw)ftanφb

(2)

式中：c′和φ′分别为有效内聚力和有效摩擦角，(°)；σn为法向应力，N；ua和uw分别为孔隙空气压力和孔隙水压力，kPa；φb为与土壤吸力(σa-uw)相关剪切强度的摩擦角，(°)。

1.3 蒙特卡罗抽样法

在SLOPE/W中采用蒙特卡罗方法对随机数生成函数进行随机抽样。每个随机数N与输入参数具有相同的分布。那么可以通过式(3)计算每个确定性分析所需的参数P：

P=μ+Nσ

(3)

式中:μ为平均值;σ为参数的标准偏差。

理论上，在蒙特卡罗方法分析时，使用的试运行次数越多，解决方案的精度就越高，但需要的计算时间就越长。在实际分析中，可以使用试验测试来确定试验次数，也就是说，可以对同一案例使用某些试验进行多次分析，如果可以接受多次分析结果之间的差异，则试验次数就足够了。

1.4 不稳定概率的计算

不稳定概率是指安全系数小于1.0的概率。对于安全系数小于1.0的情况，不稳定概率可以通过对概率密度函数下的面积进行积分计算得到。在数值分析中，可通过式(4)计算：

Pf=nf/n

(4)

式中：nf为安全系数小于1.0的分析次数；n为试验次数，取500 000。

2 降雨过程分析

根据《河北省中小流域暴雨洪水计算手册》中河北省某市的降雨量计算结果得出，100年一遇(频率F=1%)和24 h持续时间的基本降雨过程如图1(a)所示。其最大强度在持续时间的中间阶段。为了研究降雨强度和降雨量的影响，本文还使用比例法计算了另外两个10年一遇和1000年一遇的降雨过程(频率F=0.1%和10%)(见图1(a))。

本研究设计了两个持续时间不同、最大强度相同的降雨过程，以研究持续时间和降雨对坝坡不稳定概率的影响，如图1(b)所示。另外设计了两个峰值时间不同、总降雨量相同的降雨过程(如图1(c))来研究早期或晚期强度峰值的影响。用于研究降雨过程曲线形状影响的另外两个不同形状的降雨过程和总降雨量如图1(d)所示。

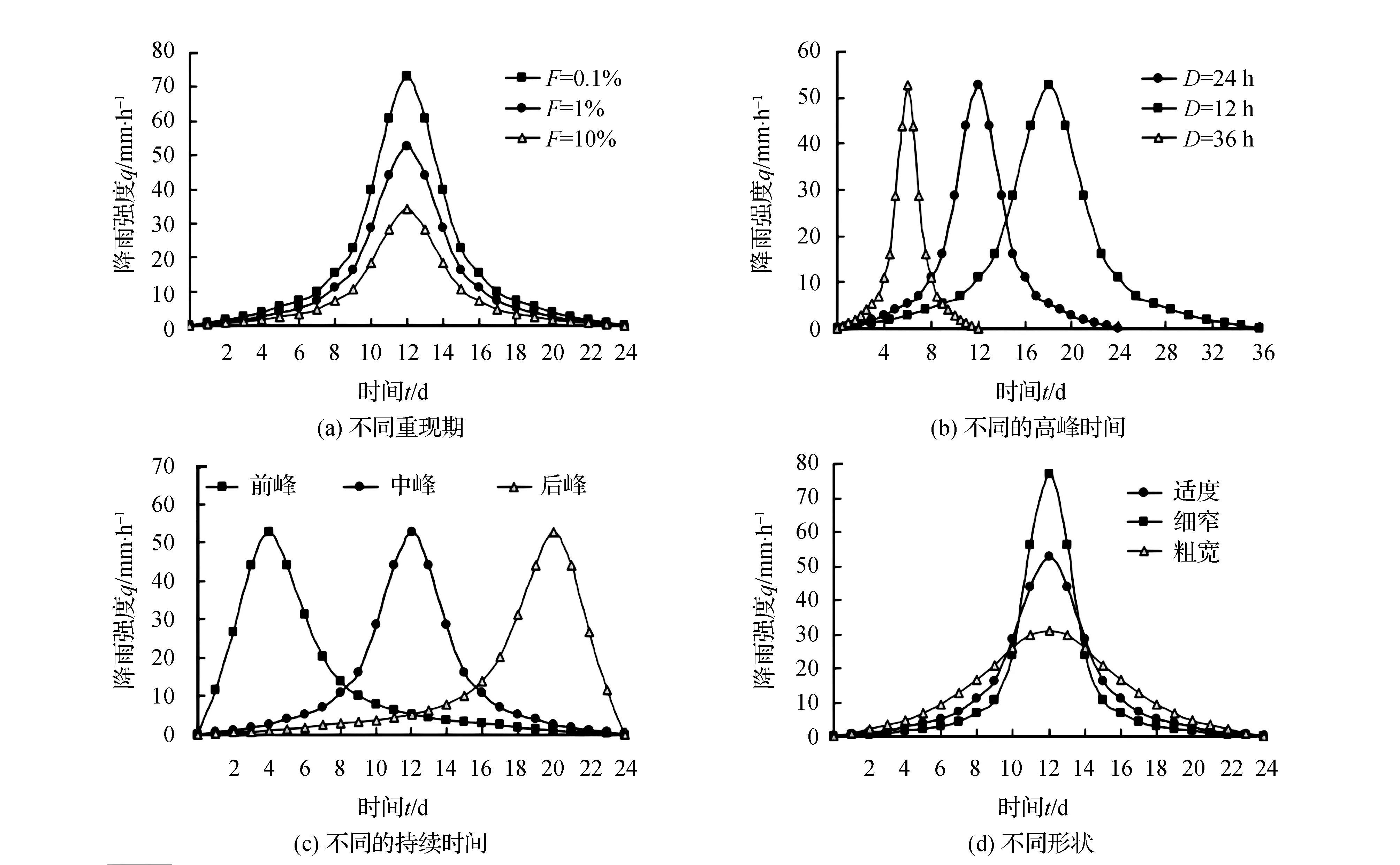
图1 分析中使用的降雨过程

本文设计了一个20 m高的黏土心墙土坝的剖面图(如图2所示)，旨在对图1中的所有降雨模式进行瞬态入渗分析。大坝的核心和外壳材料分别为黏土和细砂。在降雨期间和降雨后进行边坡稳定性分析和概率计算。由于下游边坡通常为非饱和边坡，且较易受降雨入渗影响，因此分析主要集中在下游边坡。

针对图1中不同的降雨模式，设计了4个分析组，以研究降雨强度、持续时间、强度峰值位置和降雨过程曲线形状对下游边坡不稳定概率和安全系数的影响。在每个分析组中，有3个分析案例，包括一个基本案例和两个不同的案例，如表1所示。

在本研究中，初始状态是对应上游水位为18 m 时的稳定渗流状态。渗流分析的边界条件如图2 所示，并适用于所有分析案例。每个降雨过程被视为由降雨入渗过程函数给出的单位通量边界，并应用于下游坡面。

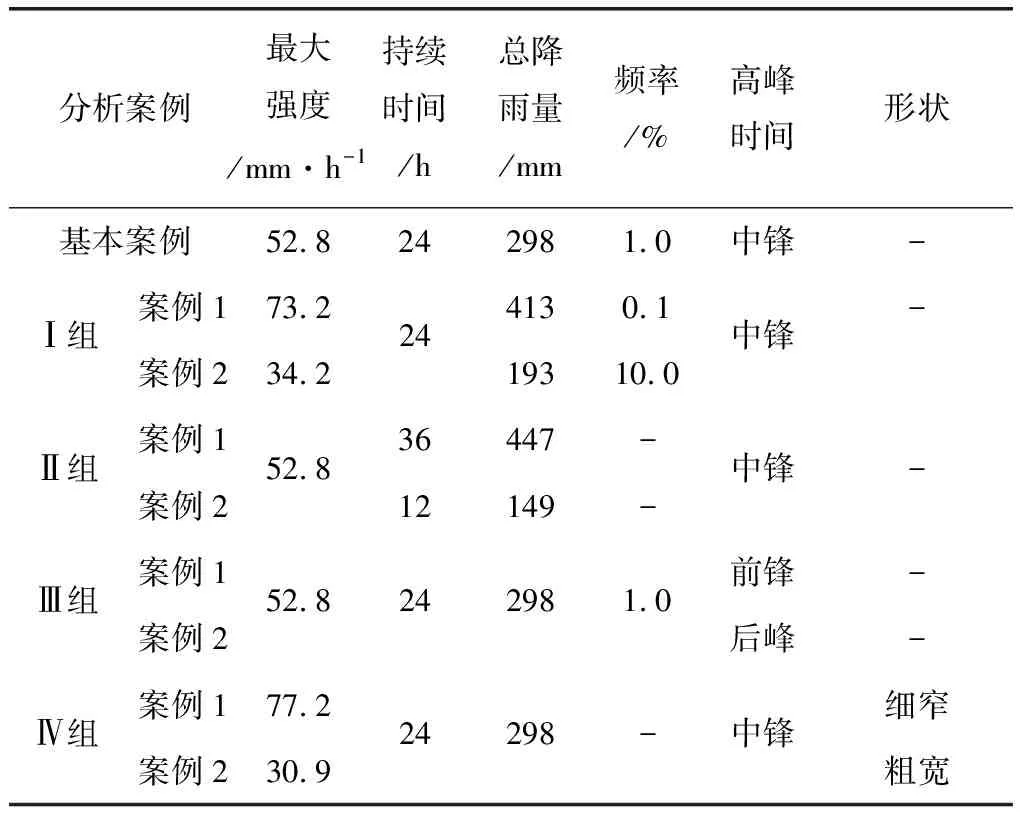
表1 分析案例及相应的降雨参数

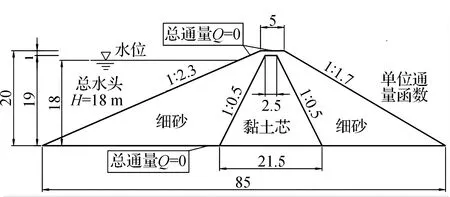
图2 分析中使用的心墙土坝剖面(单位：m)

根据经验，对大坝黏土和细砂的强度、水力特性进行了假设。将与吸力相关的摩擦角等强度参数视为随机变量。其标准偏差是基于对数十种大坝材料强度不确定性的调查。土壤的饱和渗透系数、强度参数及其标准偏差见表2。分析中使用黏土和细砂的土壤-水特征曲线(SWCC)和渗透函数如图3所示。

表2 分析中的输入参数

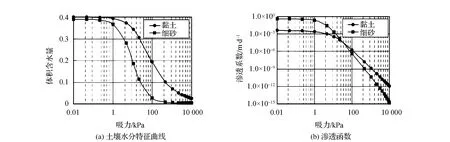
图3 黏土和细砂的SWCC和渗透函数

3 结果与讨论

在降雨期间和降雨后200 d内进行了稳定性分析和概率计算，分析结果如图4所示。在这些图中，“IP”和“FS”分别表示不稳定概率和安全系数。

图4显示了分析组Ⅰ(不同频率的降雨过程)不稳定概率和安全系数随时间的变化。在1 d降雨期间，所有情况的不稳定概率均随时间增大。1 d后，不稳定概率先增大，一段时间后达到最大值，然后随时间减小。随着降雨重现期的增加，不稳定概率增大，并且不稳定概率达到最大值的时间缩短。这表明，在降雨期间和降雨后，不稳定概率随着降雨强度和降雨量的增加而增加。降雨强度和降雨量越大，不稳定概率越早达到最大值。在Ⅰ组的所有情况和整个分析期间，安全系数随时间的变化与不稳定概率的变化相反。此外，最大的不稳定概率对应于最小的安全系数。这是因为蒙特卡罗概率方法是在某个临界滑动面上进行的。

图4 分析组Ⅰ的不稳定概率和安全系数随时间的变化(不同频率)

图5显示了分析组Ⅱ(不同持续时间、相同最大强度的降雨过程)不稳定概率和安全系数随时间的变化。在降雨期间，3种情况的不稳定概率均随时间增加。如果降雨持续时间较短，不稳定概率在较短的时间内增加得更快。因此，持续时间为0.5 d的降雨情况下不稳定概率大于0.5 d内的其他两种情况。然而，在大约0.65 d后，不稳定概率在3种情况中变得最小。降雨后，不稳定概率在一段时间内增加并达到最大值，然后随时间逐渐减小。不稳定概率达到最大值的时间随降雨持续时间的延长而减小。这表明，如果降雨持续时间更长，降雨量更大，更多的水会渗入大坝，导致吸力下降得更快更多。Ⅱ组案例的安全系数先减小后达到最小值，然后随时间的推移而增大。其变化与不稳定概率的变化相反。

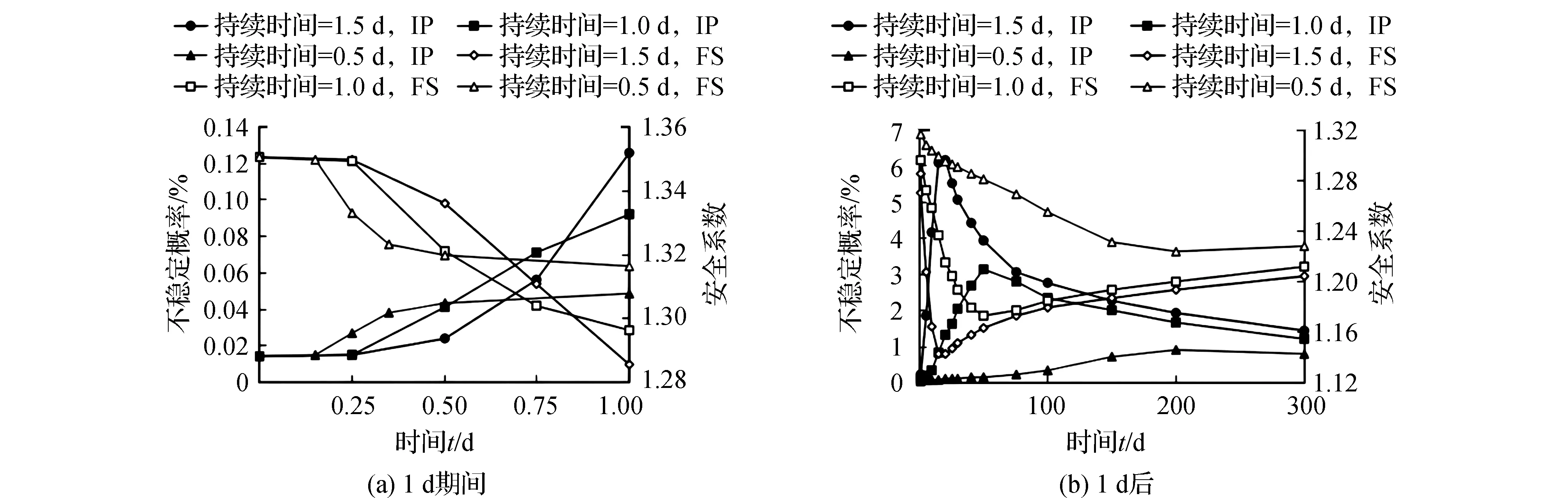
图5 分析组Ⅱ(不同持续时间)不稳定概率和安全系数随时间的变化

图6显示了分析组Ⅲ(最大强度不同位置的降雨过程)不稳定概率和安全系数随时间的变化。在1d降雨期间，3种情况的不稳定概率均随时间增加。前峰降雨的增长率在开始时较快，最后较慢；相反，后峰降雨呈现出先慢后快的趋势。降雨后，后峰降雨情况下的不稳定概率增加最快，其峰值在3种情况中最高。然而，前峰降雨的不稳定概率峰值最低。这说明，如果强度峰值较晚时，不稳定概率较大，因为峰值较早的降雨导致坝坡中的吸力减小，土体渗透性增加，水更容易渗透到土壤中，强度峰值较晚导致吸力进一步减小。因此，对于土坝边坡稳定性而言，后峰降雨的危害比前峰和中峰降雨的危害更大。

图7显示了分析组Ⅳ(不同曲线形状、相同降水量的降雨过程)的不稳定概率和安全系数随时间的变化。在降雨期间，3种情况的不稳定概率均随时间增加。降雨过程曲线粗而宽的情况下不稳定概率最大。降雨后，3种情况的不稳定概率仍在增加，同时达到最大值，然后随时间减小。在整个分析期间，降雨过程曲线细而窄的情况下不稳定概率最小。结果表明，对于坝坡稳定而言，过程曲线粗而宽的降雨比过程曲线细而窄的降雨更危险。

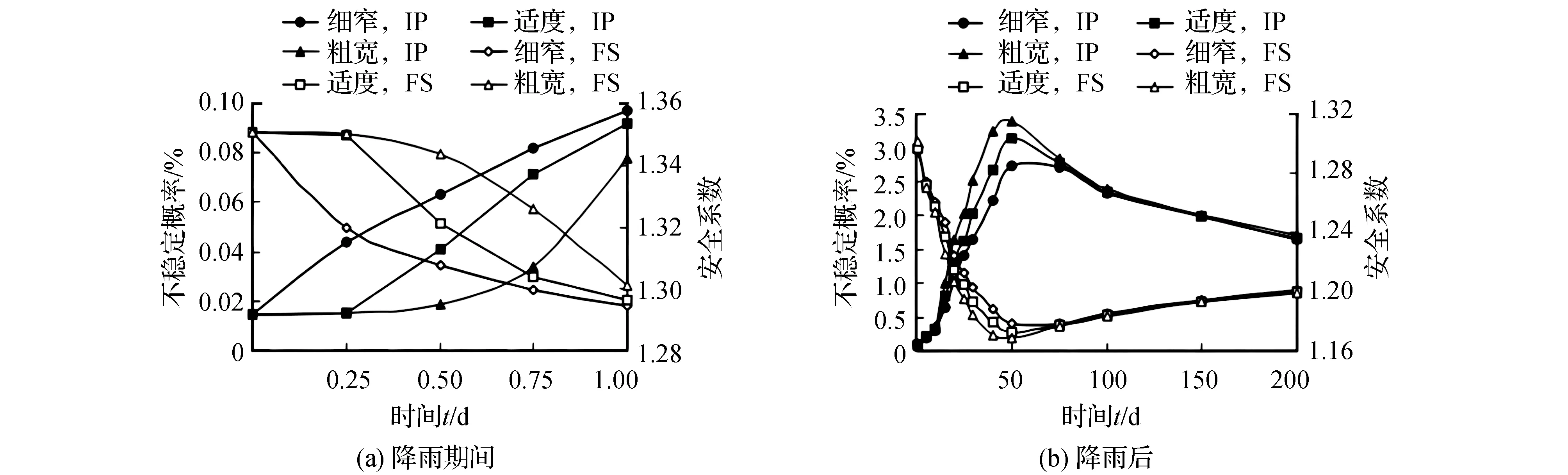
图6 分析组Ⅲ(不同峰值位置)不稳定概率和安全系数随时间的变化

图7 分析组Ⅳ的不稳定概率和安全系数随时间的变化(不同的过程曲线形状)

将图4、图5与图6、图7进行比较，结果发现在降雨期间和降雨后，前两个分析组的不稳定概率和安全系数比后两个分析组的差异更大。这说明降雨渗入坝坡时，降雨对坝坡不稳定概率和安全系数有很大影响。降雨量的增加，不稳定概率随之增加，安全系数随随之降低。降雨量越大，不稳定概率和安全系数越早达到极值。

4 结 论

本文利用渗流分析软件SEEP/W研究了降雨入渗对坝坡不稳定概率和安全系数的影响。基于本研究的结果得出以下结论：

(1)对于所有分析案例，不稳定概率在降雨期间和降雨后一段时间内增加，然后随时间降低。

(2)在整个分析期间，安全系数随时间的变化与不稳定概率的变化相反。

(3)坝坡不稳定概率随降雨量、降雨强度和降雨持续时间的增加而增加。降雨量越大，坝坡不稳定概率达到最大值的时间越短。

(4)由于前期降雨时间较长，后峰降雨会导致坝坡不稳定概率较高，安全系数较低。

(5)粗而宽的降雨过程曲线将导致更高的不稳定概率和更低的安全系数。