基于FLAC 3D分析下河道岸坡填土体静、动力场特征研究
2022-10-13刘延厚
刘延厚
(洛阳水利勘测设计有限责任公司,河南 洛阳 471000)
河道堤防安全稳定性与岸坡密切相关[1-2],而岸坡稳定性牵涉面较广,其填土体特征、堤防迎水侧水位等均会影响岸坡在静、动力场中表现[3-4],故而评价堤防岸坡稳定性不仅需要考虑静力场安全系数变化,对地震动力作用下亦要开展研究,特别是地震地质构造带活动区域。张庆海等[5]、张磊[6]、李西伟[7]根据岸坡填土体力学稳定性问题,通过在室内设计开展土体压缩、剪切及渗透特性试验,获得了岸坡填土体渗透、力学受自身因素影响变化特征,为岸坡加固提供了基础试验依据。薛一峰等[8]、董武斌[9]利用ANSYS、FLAC 3D等仿真计算软件建立了边坡模型,以实际工况下所受荷载开展应力、位移计算,分析边坡安全稳定性演化特征,为工程针对性建设提供计算佐证。岸坡填土体动力响应特征关乎岩土体本构响应关系,梁学斌[10]、寇卫锋[11]、王学洲等[12]利用仿真手段可以提取地震波荷载,施加在岸坡土体上,研究岸坡自振特性及地震动响应特征,为评价岸坡抗震特性提供综合佐证。本文针对伊洛河流域内典型岸坡多层填土体安全稳定性问题,利用仿真手段分别开展了静力场计算与EI Centro地震波动力响应分析,为岸坡填土体加固处理提供参考。
1 工程设计模拟
1.1 工程概况
伊洛河堤防距城市中心区约5 km,辐射城区面积超过15.52 km2,全河道总长约为446.9 km,流域面积超过1.89 km2,在洛阳市境内面积占比约为25%,设计加固堤防河道占境内堤防长度的38%,伊洛河段平均河宽约202 m,过水断面面积15 295~16 289 m2,高程约34.00 m。伊洛河上游建设有蓄水库与泄洪闸,控制陕西与河南交界河段内水利流量,最大泄流量为525 m3/s,区域内最大降雨量日不超过800 mm。由于河南2021年“7·20”特大暴雨导致局部伊洛河堤防出现非稳定性,局部堤防监测传感器得到渗透坡降及坡身压强超过警戒值,表明洛阳市境内伊洛河堤防出现不稳定性,亟需加固防渗。目前伊洛河岸防洪堤防采用堆土坝,市区内长度为5~9 km,堤顶高程约36.8~38.6 m,堤顶宽度6~10 m,设计有交通车道等,但局部区段内堤防顶路面受堤身水土流失及水力冲刷作用,硬化路面破损较严重,交通极易拥堵。根据对伊洛河堤防勘测得知,全长河道受水土流失影响差异较大,在洛阳伊洛河境内开始桩号T0+000~T0+860,河段内含沙量低于5 kg/m3,河流内水生态体系较佳,无显著水土流失作用,堤顶高程37.0~38.0 m,究其根本乃是其堤身采用生态护坡与混凝土砌块硬化结合形式设计[13],有效确保了堤身安全稳定性,堤身内最大渗透坡降不超过0.22,坡内孔隙水压力稳定在40 kPa以下。在洛河与伊河交界汇入处,即桩号TO+860~T1+880,堤坡较陡,此区段内为重点加固段,采用碎石土分层压实,实际效果还有待进一步探讨。由于伊洛河乃是洛阳境内主要地表水来源,也构成了区域内各大小支流汇入目的地,因而,伊洛河堤防不仅需要考虑迎水侧渗流安全,对背水侧静力场稳定性也必须考虑,特别是堤防加固段由于工程填土扰动等影响,导致局部堤防岸坡出现覆土增大等效应。在伊洛河堤防桩号T3+120~T4+340区段内,由于堤顶高程起伏影响,采用堤防心墙坝形式,如图1几何设计模型,防浪墙可有效降低堤身受水力冲刷影响,但该区段内也受河道清淤影响,堤身岸坡覆盖有填土体。从河道防洪堤防安全考虑,多个区段内堤防受到上覆填土影响,特别是在防渗加固段内,此对堤防安全稳定性具有影响,当河道水位出现骤降等不利工况时,堤段内岸坡极易受威胁。为此,工程设计部门考虑在进行防渗加固施工前,开展对重点河段堤防岸坡上覆填土体稳定性研究,确保工程建设安全。

图1 心墙堤坝几何模型
1.2 工程设计
针对伊洛河堤防岸坡填土体安全,本文以堤防加固段T1+800处岸坡为分析对象,该处岸坡填土体按照分层堆筑,每层高度为1 m,共有6层,坡度1/2.5,底部按照图1心墙堤坝设计形式,设置有石笼挡墙结构,高度为5.5 m。基于工程实际,采用FLAC 3D仿真平台建立岸坡几何模型[14]。
经网格划分获得静力场计算模型,所得网格26 128个,节点数12 783个。坡内土体以粉质壤土、砂土物理力学参数设定,而填土体按照岸坡实际土体实测土工参数计算。由于计算模型中实质上是多层填土体构成,而每层填土体交界面上的摩擦度与其压实度密切相关,笔者为探讨分层压实度效果对岸坡填土体稳定性影响,在有限元模型中以填土体交界面摩擦系数反映分层压实度,分别设定压实度为50%、60%、70%、80%、90%,相应土层交界面上渗透系数分别设定为9.2×10-5cm/s、9.0×10-5cm/s、8.8×10-5cm/s、8.6×10-5cm/s、8.4×10-5cm/s,堤防迎水侧水位分别设定为19.5 m、21.5 m、23.5 m、25.5 m、27.5 m、29.5 m、31.5 m,探讨在不同工况下堤防岸坡填土体静力与动力稳定性特征。
2 堤坝岸坡填土体静力学特征
2.1 迎水侧水位影响
根据对不同迎水侧水位工况下岸坡填土体开展静力计算,获得各工况中岸坡应力分布特征,如图2所示。从图中可看出,当迎水侧水位愈高,则岸坡填土体应力分布水平愈大,在水位19.5 m工况下岸坡内最大应力为841.2 kPa,而水位23.5 m、25.5 m工况下岸坡最大应力较前者分别增长了27.3%、42.5%,当从整体迎水侧水位影响填土体应力水平可知,迎水侧水位每增长2 m,则岸坡内最大应力水平可增长11.4%。分析表明,当堤防迎水侧水位增大,其对岸坡内土体水力渗透作用加大,进一步导致土体内形成渗透通道,无形中增大了土体滑移可能性,进而导致坡内应力水平增大[15]。分析坡内应力分布特征可知,在各工况中,岸坡填土体应力从坡顶至坡底,均为递增状态;以水位23.5 m工况下为例,其在坡体表面上应力水平约为88 kPa,而在坡底处应力水平增大了10倍。因而,从堤防护坡设计考虑,应重点关注堤防坡底部位,此处应力主要受到上覆填土体影响。
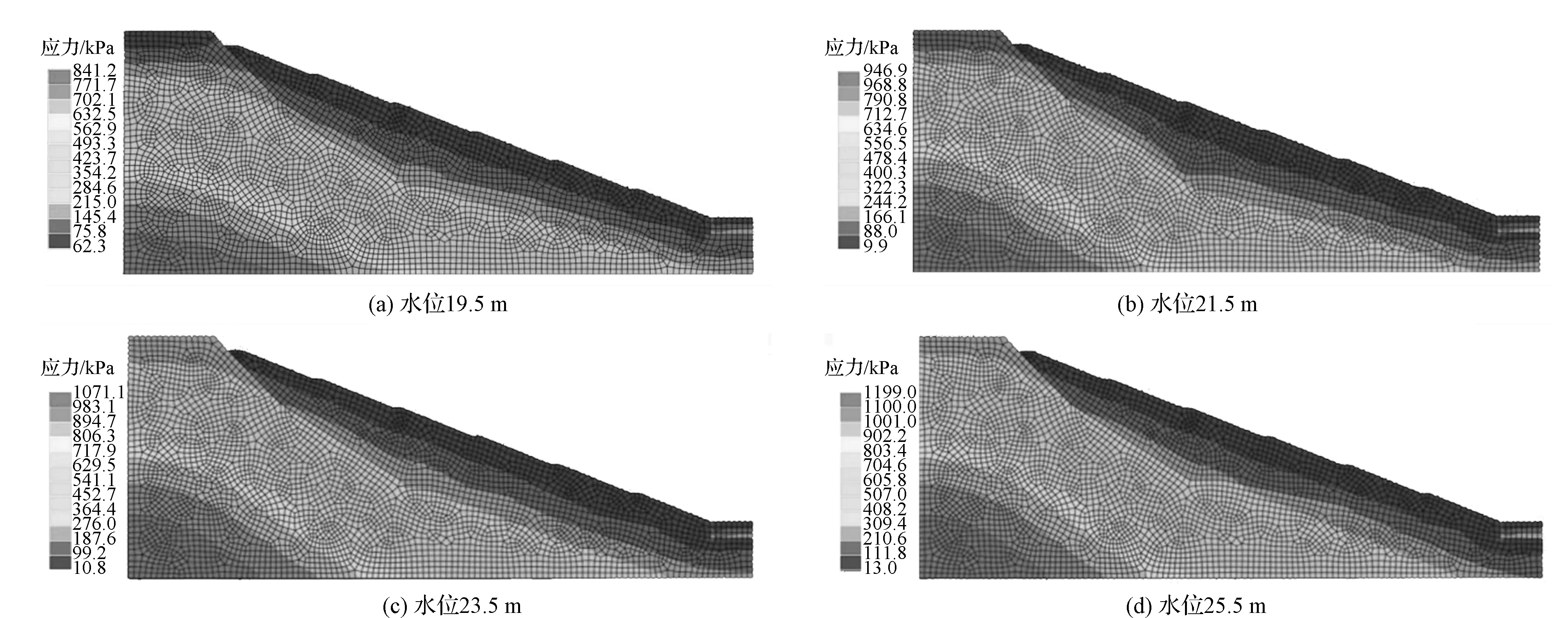
图2 岸坡应力分布特征
同理,可获得不同水位工况下岸坡内位移分布特征,如图3所示。根据图中位移分布可知,迎水侧水位与坡内最大位移为正相关变化,在水位23.5 m工况下最大位移为0.673 m,而水位25.5 m、29.5 m工况下最大位移较之分别增大了19.2%,当水位每增大2 m,平均可导致坡内填土体最大位移增长12.3%。从位移分布来看,其在坡内各高程上演变特征与应力演化有所类似,均从坡顶至坡底为递增,此也表明了岸坡内应力、位移的来源为土体自重[16],从护坡设计考虑,应重点防护土体自重应力导致的滑坡失稳。

图3 岸坡位移分布特征
根据对不同水位工况下岸坡稳定性计算,获得了各工况下堤防岸坡安全稳定系数变化特征,如图4所示。分析安全系数变化可知,堤防迎水侧水位愈大,则岸坡安全系数愈低,水位每增大2 m,岸坡安全系数平均可递减18.3%;但不可忽视,安全系数降幅处于增大的过程,在水位为19.5~25.5 m方案内,安全系数平均降幅仅为7.1%,但水位超过25.5 m后,安全系数最大降幅达38.4%,平均降幅为35.1%,甚至在水位29.5 m工况下安全系数低于1。由此可知,堤防迎水侧水位处于安全运营期,仍然会对岸坡稳定性产生较大威胁,故岸坡加固很有必要。
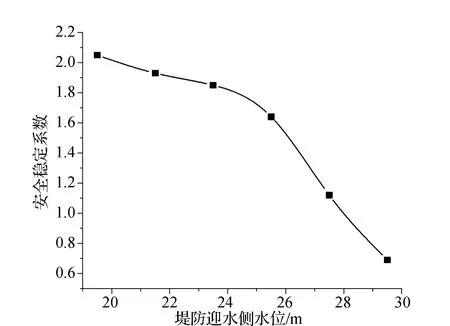
图4 堤防岸坡安全稳定系数变化特征
2.2 分层压实度影响
根据对不同压实度下岸坡填土体静力场计算,获得岸坡内应力分布特征,如图5所示。分析图中应力分布可知,当填土体分层压实度改变,各工况下岸坡应力分布差异性较小,而最大应力增幅也较小,在压实度50%下最大应力为83.8 kPa,而压实度70%、90%下最大应力分别为84.1 kPa、84.3 kPa,表明压实度对岸坡填土体内应力水平影响较小。
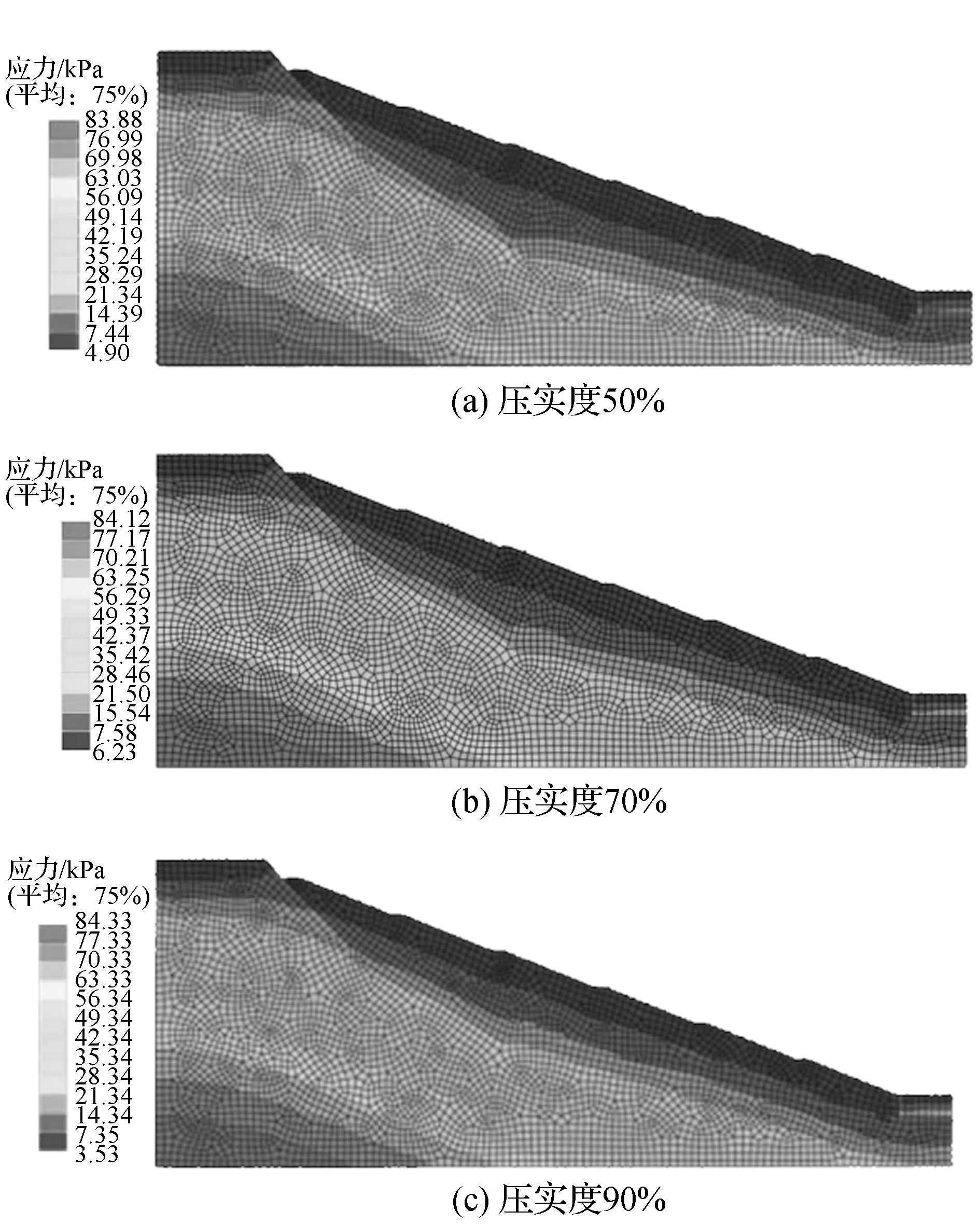
图5 各压实度方案下岸坡应力分布
图6、图7为各工况下岸坡内位移分布与变化特征。从图中可知,当在水位23.5 m时,压实度以20%的差异对比,仍然不改变各方案下位移基本相近的现象,3个压实度工况下最大位移的差距最大仅为0.1%,基本均稳定在0.738 m左右。而对比其他水位下压实度工况也可知,基本上压实度的差异,对位移特征无显著影响,同一水位下各压实度工况内的位移特征基本表现一致,此种现象与应力受之影响类似。
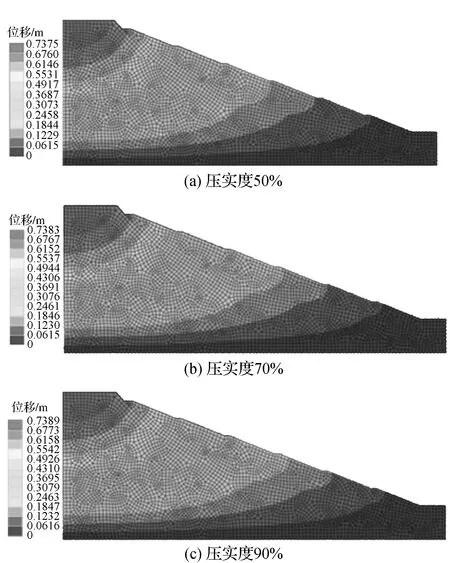
图6 各压实度方案下岸坡位移分布
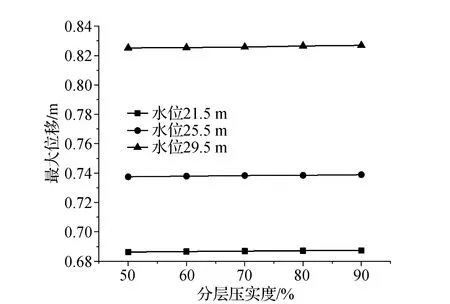
图7 各压实度方案下岸坡最大位移变化
根据静力场计算获得各压实度工况下岸坡安全稳定系数变化特征,如图8。分析安全系数演变可得知,同一水位下,压实度增大,安全系数稍有增长,在水位25.5 m工况下,压实度每增大10%,安全系数平均可提高3.9%,而在其他水位下,安全系数随压实度变化而影响平均增幅为3%~4%,即压实度的提高,有利于岸坡稳定性,但促进效应有限。
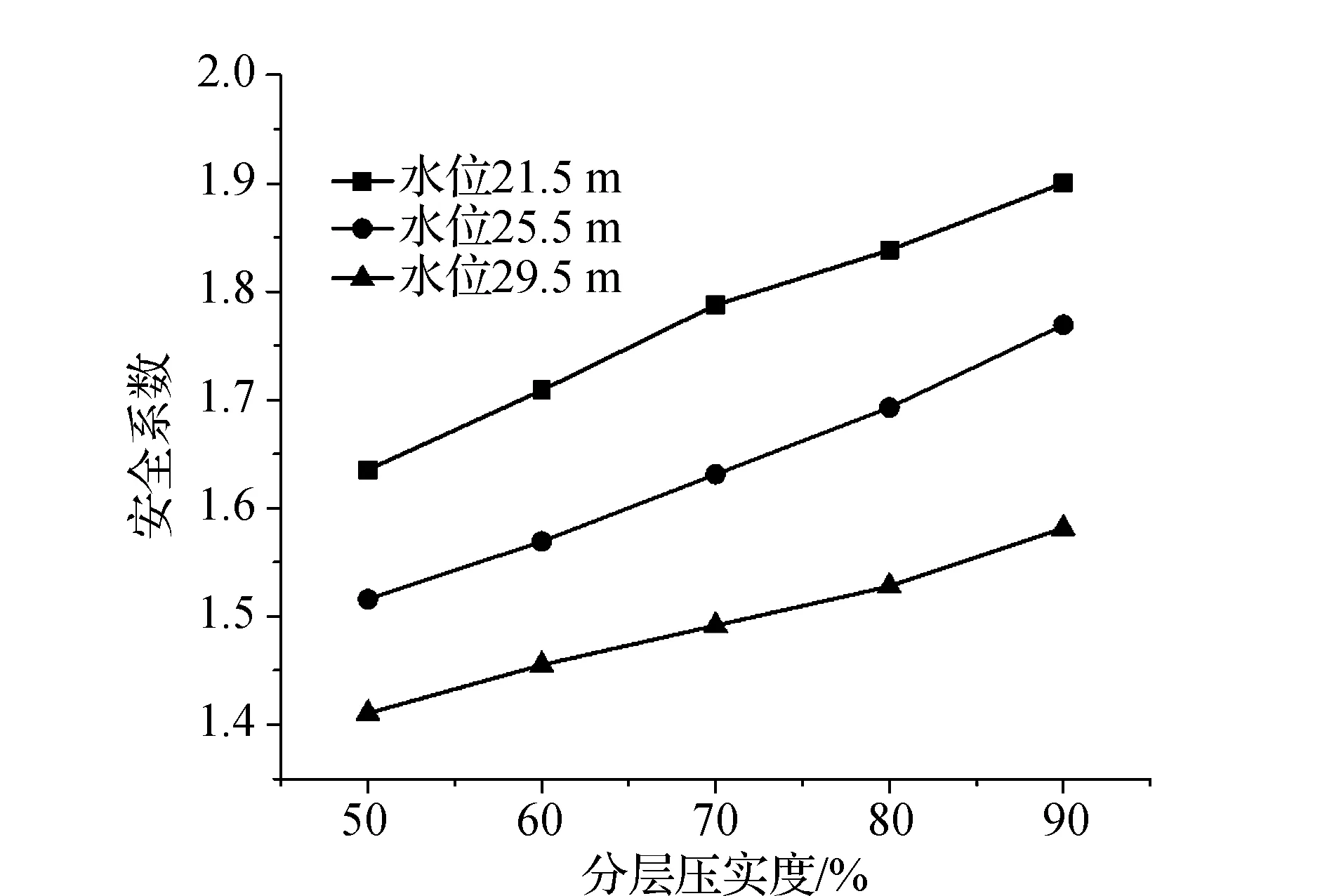
图8 各压实度方案下岸坡安全系数变化
3 堤坝岸坡填土体动力学特征
基于EI Centro地震波输入[17],设置地震水平系数为0.5,峰值加速度设定为0.25 g,计算获得岸坡填土体稳定性特征及地震动响应特性,图9为地震作用下岸坡填土体内应力、位移分布特征。
从图中可看出,在地震动力作用下,其最大应力分布为819.4 kPa,较之静力作用下,地震动力水平作用受静水压力削弱平衡影响,导致填土体最大应力水平并未达到1000 kPa,相比静力场下最大应力,动力作用下最大应力增长约为10倍。从位移分布特征可知,与静力场位移分布有所差异的是,地震动力作用下最大位移分布由坡底转移至上覆填土体区域,且在0.25 g峰值加速度地震波作用下,岸坡上覆填土体接近临界破坏。
针对岸坡填土体地震动影响特征,本文以六层填土体接触面上特征点作为分析对象,获得典型层面上地震动加速度响应特征,如图10所示。从各层面上峰值加速度响应值可知,第一层面上峰值加速度响应值为0.045 m/s2,而在第三、第五层面上峰值加速度较前者分别增长了82.2%、4.56倍,从第一层至第五层填土层面上峰值加速度响应值均为递增。从填土体分层特征可知,第一至五层高程上为从坡顶延伸至坡内,故坡内峰值加速度响应表现以填土体下部更为显著,失稳破坏也是从填土体下部开始[18]。

图9 地震作用下填土体内应力、位移分布特征

图10 填土体加速度响应特征
图11为地震动作用下岸坡内各计算阶次内的位移响应特征。分析图中各层面位移特征可知,第一、三、五层面上位移响应最大值分别为0.025 m、0.015 m、0.022 m,对比各层面位移响应值可知,填土体中部较为稳定,位移响应值低于上、下部,故填土体的加固处理重点应在填土体表面与下部区域。
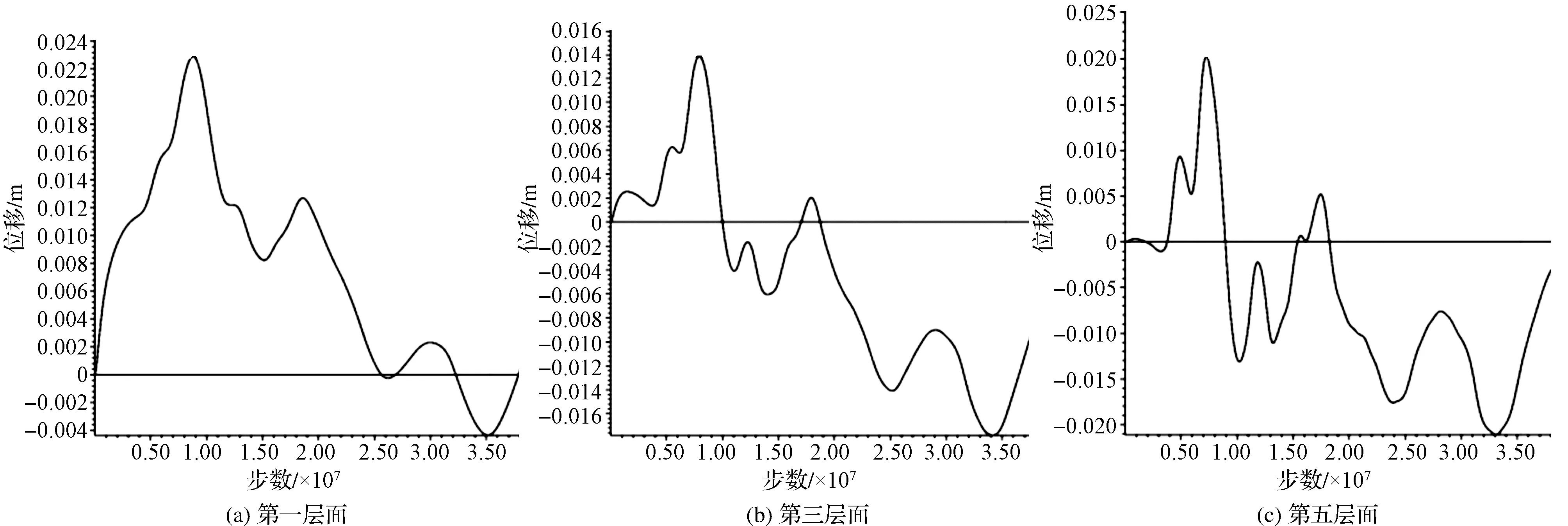
图11 填土体位移响应特征
4 结 论
(1)堤防迎水侧水位愈高,则岸坡填土体应力与位移水平愈大,但岸坡安全系数为递减,水位每增长2 m,则最大应力与最大位移可增长11.4%、12.3%,而安全系数平均可递减18.3%;岸坡填土体应力、位移均从坡顶至坡底为递增演变。
(2)分层压实度对岸坡填土体应力、位移分布影响较小,压实度50%、70%、90%工况下最大位移基本均稳定在0.738 m;压实度增大,安全系数稍有增长,但增幅有限,安全系数随压实度变化而增幅平均为3%~4%。
(3)地震动力作用下填土体最大应力未超过1 MPa,最大位移分布由坡底转移至上覆填土体区域;岸坡峰值加速度响应表现以填土体下部更为显著,而填土体中部位移最为稳定。
