错列双圆柱涡激振动干涉数值模拟*
2022-10-13王晓凯赵德光
张 睿 娄 敏 王晓凯 赵德光
(1.中国石油大学(华东)石油工程学院 2.海洋石油工程(青岛)有限公司)
0 引 言
随着海洋油气的开发,海洋立管作为海上油气开发中最为关键和易损的部件,其涡激振动问题受到广泛关注[1]。在实际工程中,一座海洋平台通常会连接多根海洋立管,立管与立管会形成多圆柱系统。不同于单根圆柱的涡激振动,由于存在立管间尾流干涉的影响,多圆柱系统产生的涡激振动特性更为复杂[2-3]。
杜晓庆等[4]通过数值模拟对串列圆柱中上游圆柱的运动状态对下游圆柱涡激振动的影响进行了研究,发现上游圆柱的振动会提高下游圆柱的起振速度和横流向最大振幅,并且两类串列圆柱在振动过程中的间距比和下游圆柱发生涡激振动的机制都有所不同。王晓凯等[5]在尾流干涉下考虑流固耦合作用对小尺寸串联圆柱进行仿真研究,发现串联圆柱的尾涡脱落模式随约化速度增大会发生显著变化,进而影响圆柱的运动响应和受力情况。林凌霄等[6]基于CFD方法,对不同间距比下的并列双圆柱绕流进行了数值模拟,模拟结果表明,随着间距比的改变,两圆柱尾流会呈现不同的形态。F.J.HUERA-HUARTE等[7]通过试验研究了高雷诺数下柔性并联双圆柱的流致振动,发现当间隙比大于2.5时,两圆柱之间的干扰耦合影响较小。叶泽华等[8]在改进CBS(Characteristic Based Split)有限元求解流场的基础上,通过改进的流-固耦合有限元解法计算涡激振动问题,模拟了低雷诺数下两错列圆柱涡激振动过程,发现来流角度改变对于下游圆柱的流场、受力及振动特性有着显著影响。徐万海等[9]采用模态分析法将试验测量应变转化为位移,开展了3种排布方式下双柔性圆柱流激振动的模型试验,试验结果表明,当柔性圆柱交错排布时,下游圆柱横流向和顺流向的控制频率接近,顺流向的位移显著增大。
目前,对双圆柱系统的研究主要集中在固定圆柱绕流特性及串、并联基础布置的涡激振动研究上。在工程实际中,两圆柱错列排布相比串联或并联情况更为常见,然而关于错列双圆柱涡激振动特性的研究还相对较少[10]。为进一步探究影响错列双圆柱涡激振动特性的敏感间距及排列角度,笔者基于重叠网格(Overset Mesh)技术进行网格划分,将振动模型简化为双自由度系统,建立二维流固耦合数值模型,使用四阶龙格库塔法求解振动方程,编译用户自定义函数(UDF)并结合Fluent动网格技术进行求解,在对所建模型进行验证的基础上,对错列双圆柱开展涡激振动响应研究,研究间距比、来流角度和约化速度对错列双圆柱涡激振动特性的影响。所得结果可为实际海洋立管的布置提供参考。
1 数值方法
1.1 控制方程
连续性方程和动量方程:
∇u=0
(1)

(2)
式中:u表示流体的速度,m/s;p表示压力,Pa;Re表示雷诺数;t表示时间,s。
将圆柱振动模型简化为二维弹簧-质量-阻尼系统,振动模型控制方程如下:
(3)
(4)
式中:x、y分别为圆柱顺流向和横流向位移,m;m为单位长度质量,kg/m;c为阻尼系数,N/(m/s);k为刚度系数,N/m;FD(t)、FL(t)分别为顺流向和横横向的流体力,N。
1.2 流固耦合实现
针对立管的涡激振动问题,本文采用动网格技术实现流固耦合,具体如下:通过Fluent对圆柱的运动和圆柱周围流场变化进行模拟,提取圆柱受到的升力和阻力系数;在UDF中采用四阶龙格库塔法对二维振动控制方程进行离散并求解,得到每个时间步内对应的立管速度和位移。
1.3 模型参数
本文模拟所取圆柱直径D为0.02 m,质量比m*为2.55,阻尼比ξ为0.003,固有频率为1.72 Hz。两圆柱错列排布,如图1所示。圆柱间距S为4D,来流角度α=45°,两圆柱圆心到流场中轴线的距离相同,流场域左侧距离上游圆柱圆心10D,流场域右侧距离上游圆柱圆心30D。
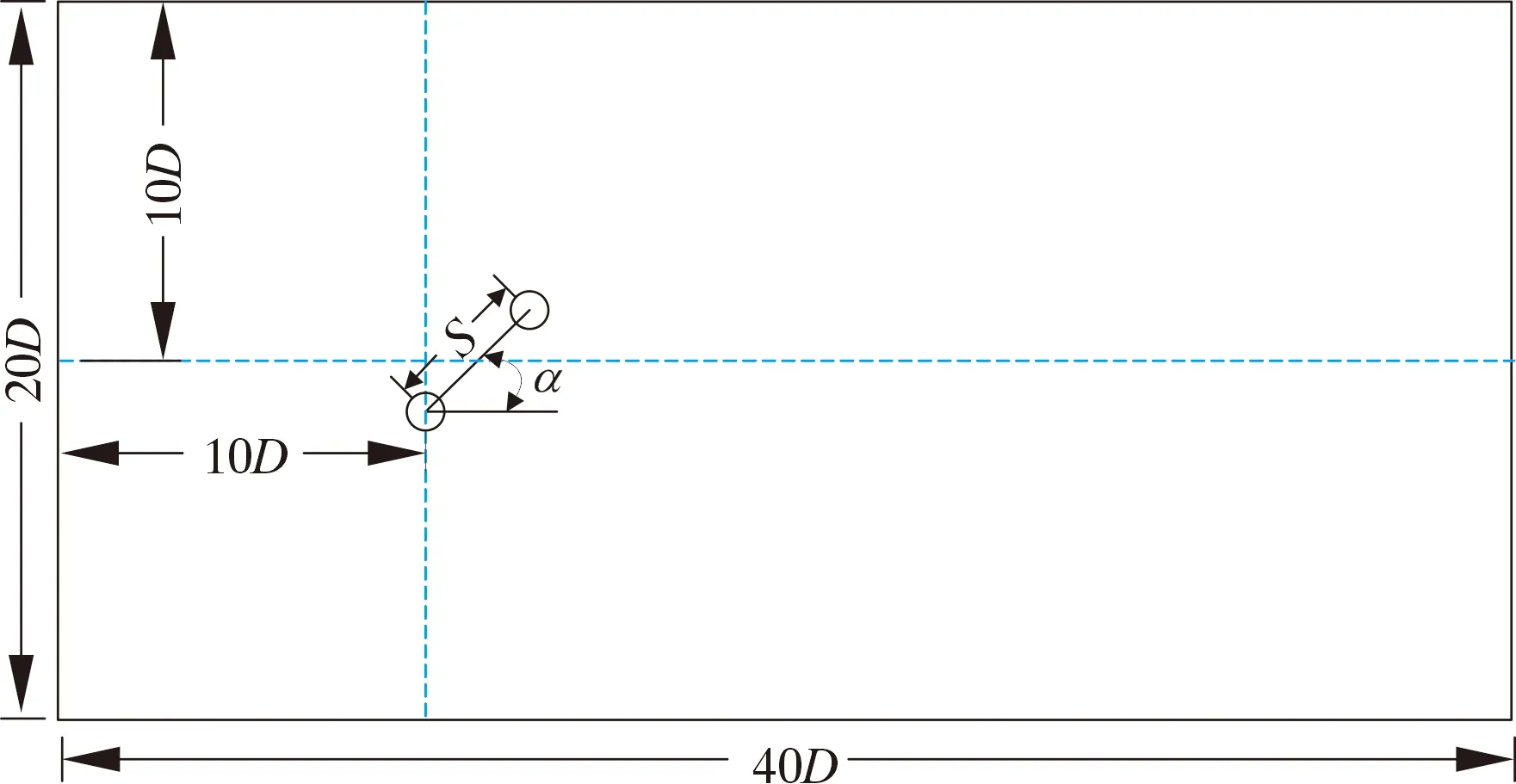
图1 圆柱排布方式图Fig.1 Arrangement of cylinders
通过Overset Mesh技术进行流场模型的网格划分[5],以保证较好的网格质量,网格划分结果如图2所示。网格类型均采用结构化四边形网格,对尾流区域的网格进行加密处理,其他区域逐渐增大网格密度,以此合理控制网格总量,以便节约计算时间。

图2 网格划分示意图Fig.2 Schematic diagram of mesh division
计算流场域入口采用均匀速度边界,出口选择压力边界,上下两侧面边界为对称边界条件,圆柱表面采用无滑移边界条件。通过湍流强度和水力直径定义湍流,计算可得湍流强度和水力直径;湍流模型采用SSTk-ω模型,对流项采用二阶迎风离散格式,时间项采用全隐式积分;通过Coupled算法实现控制方程中速度与压力的耦合。根据网格相对运动不超过划分网格的最小尺寸的要求,选取迭代时间步长为0.01 s。
2 模型验证
2.1 圆柱绕流验证
对雷诺数Re=200、间距比S/D=3时的串联双圆柱体绕流进行数值模拟,将所得结果与文献[11-13]的模拟结果进行对比,结果如表1所示。从表1可以看出,本文圆柱绕流模拟所得上游阻力系数Cd1、下游阻力系数Cd2和斯特劳哈尔数St与文献中数值结果相近,由于网格、湍流模型以及数值处理的方法不同,存在一定误差。这说明本文所采用的网格划分方法、计算模型设置的参数以及模拟结果正确。
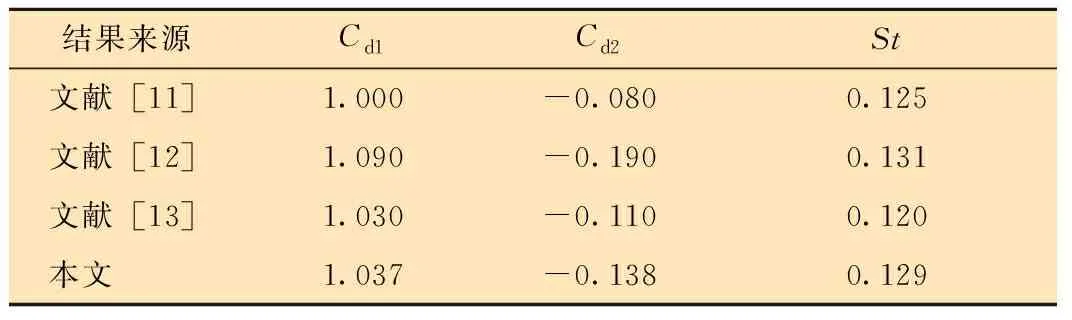
表1 双圆柱绕流模拟结果对比Table 1 Comparison of simulation results of flow around double cylinders
2.2 单圆柱涡激振动模拟验证
由于圆柱流固耦合研究涉及到流场网格的动态变化,与圆柱绕流相比,对网格质量、计算参数选取及自定义函数的准确性等有着严格的要求,所以需要对圆柱模型进一步开展模拟验证。
计算模型采用前文的网格划分方法及数值求解格式要求,严格按照文献[14-15]中的参数进行数值模拟,将本文模拟结果与文献结果进行对比,结果如图3所示。
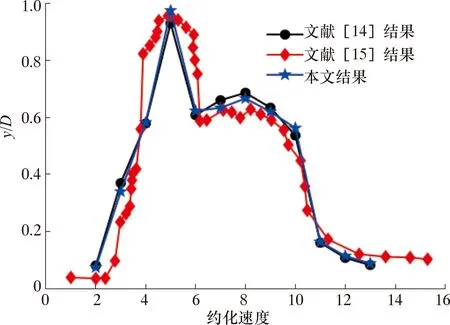
图3 横流向振幅随约化速度的变化关系Fig.3 Variation of transverse amplitude with reduced velocity
采用振幅均方根与圆柱直径之比(y/D)对横流向振动响应进行描述。从图3可以看出,本文模拟结果与参考文献结果相似,确定了自定义函数UDF的准确性以及流固耦合计算模型的可靠性,为后文错列圆柱涡激振动数值模拟研究奠定了基础。
3 计算结果
基于上述数值模型,选择无量纲量约化速度Ur=1.0~15.0,即雷诺数Re=680~10 320。首先对间距比S/D=3.0、4.0及5.0的错列排布双圆柱立管涡激振动特性开展研究;同时研究来流角度α=15°、45°及75°工况下错列双圆柱涡激振动特性。
3.1 错列圆柱间距比研究
3.1.1 圆柱振动频率与幅值
保持来流角度α=45°不变,在不同间距比下,错列圆柱的漩涡脱落频率fs与固有频率fn的比值λ随约化速度的变化如图4所示。由图4可知,在低约化速度范围内,不同间距比的各条曲线走向几乎一致,而在进入高约化速度范围Ur>10后,错列两圆柱的频率比在数值上存在较大差距,上游圆柱明显大于下游圆柱。
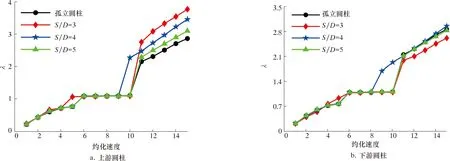
图4 不同间距比下频率比随Ur的变化关系Fig.4 Variation of frequency ratio with reduced velocity at different spacing ratios
不同间距比下错列圆柱的横流向振动响应随约化速度的变化关系如图5a和图5b所示,顺流向振动响应随约化速度的变化关系如图5c和图5d所示。
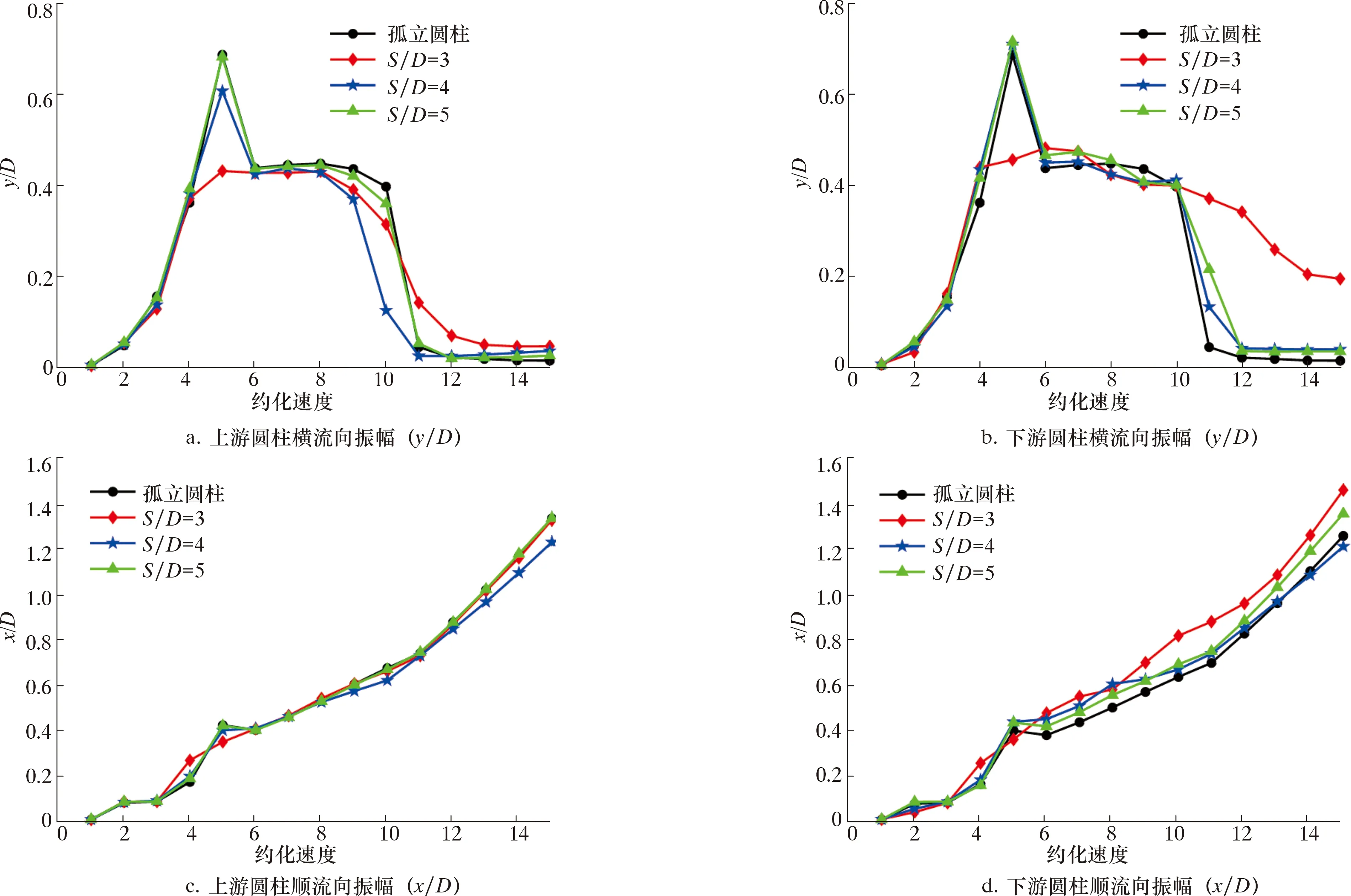
图5 圆柱涡激振动响应随Ur的变化关系Fig.5 Variation of vortex-induced vibration response of cylinder with reduced velocity
从图5可以看出,当约化速度Ur=0~4时圆柱振动处于上分支,Ur=4~10为锁振区间,Ur=10~15时处于下分支。但是间距比S/D=3时下游圆柱的曲线格外突出,在两个流向上的振幅会明显大于其他圆柱。这是因为间距较近,间隙流相当于增大了来流流速,因此下游圆柱位移幅值明显增大。随着间距比的增大,圆柱间的干涉作用减弱,上、下游圆柱的振幅曲线不断向孤立圆柱的振幅曲线靠近,横流向振幅变化呈现三段式变化趋势,顺流向平均振幅(x/D)随着来流速度的增大持续增大。
3.1.2 运动轨迹分析
圆柱运动轨迹如图6所示。由图6可知,当间距比S/D=3时,两圆柱的运动轨迹较为杂乱,无明显“8”字形,下游圆柱受上游圆柱的流动干涉影响出现了许多不稳定的非周期性运动轨迹,表明在S/D=3时错列两圆柱的流动干涉作用较为强烈。
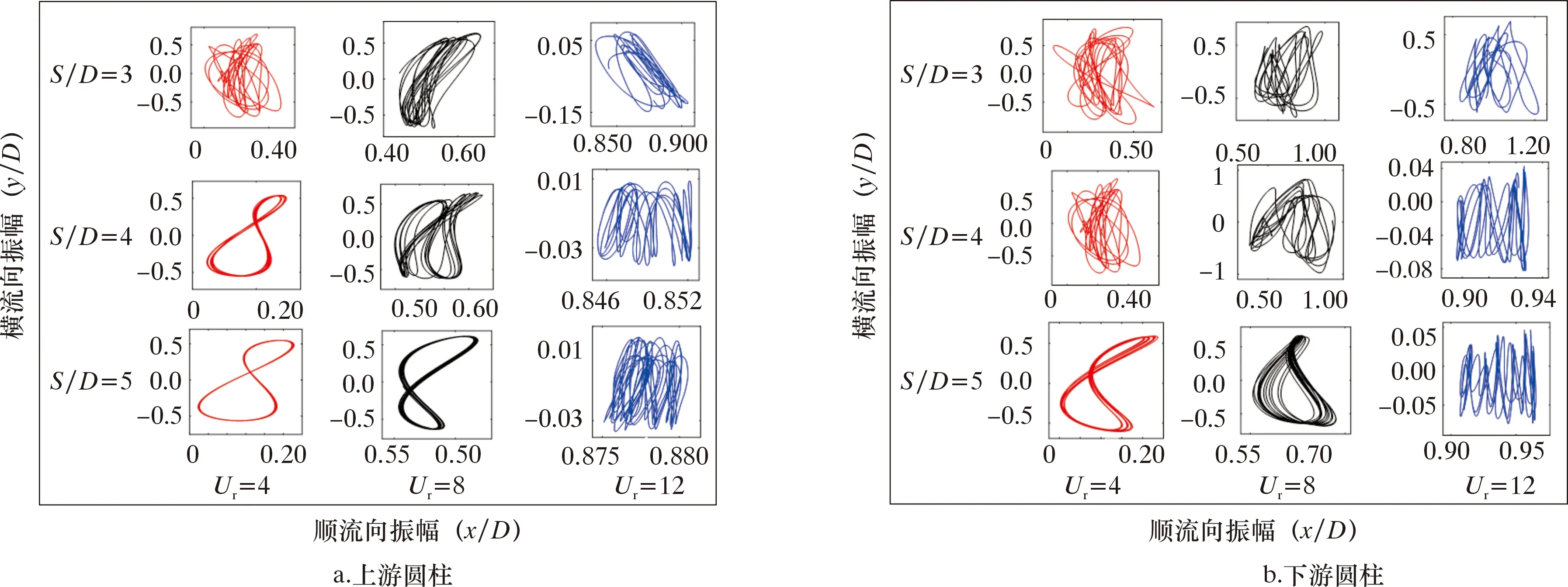
图6 两圆柱的运动轨迹(来流角度不变)Fig.6 Kinematic trajectories of double cylinders (at constant flow angle)
随着间距比的不断增大,“8”字形、“桃”形等运动轨迹开始占据主导,圆柱运动的规律性得到提升,运动轨迹由繁到简,两圆柱轨迹间的差异越来越小,上游圆柱和下游圆柱的运动轨迹随着S/D的增大慢慢趋于一致。S/D=4和5时,上游圆柱对下游圆柱的干涉效应显著高于下游圆柱对上游圆柱的干涉反馈效应。
3.1.3 流场分析
图7反映了不同间距比下错列两圆柱的尾涡模态随约化速度的变化关系。
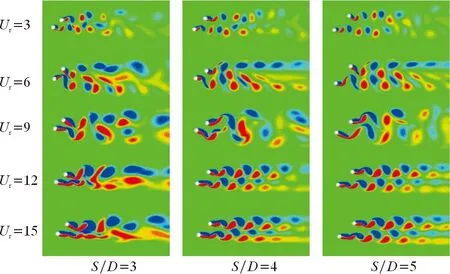
图7 不同间距比下尾涡模态随Ur的变化Fig.7 Variation of trailing vortex mode with reduced velocity at different spacing ratios
由图7可知:在间距比S/D=3时,随着约化速度增大,流体与圆柱之间的耦合作用强烈,不能在圆柱后方形成规则脱落的漩涡;当约化速度大于10后,两圆柱脱离“锁振”状态,振幅减小。S/D=3与其他间距比相比,下游圆柱受到上游圆柱尾涡脱落的影响更大,在横流向产生比其他2种情况更大的振幅;下游圆柱也对上游圆柱产生“抑制”,使上游圆柱的尾涡变得细长。在高约化速度下,随着间距比的增大,下游圆柱对上游圆柱的“抑制”作用减弱,上游圆柱出现涡旋脱落,涡街形态逐渐变得规则,直到S/D=5时,上、下游圆柱的频率比曲线逐渐接近孤立圆柱。
3.2 错列圆柱来流角度研究
3.2.1 圆柱振动频率与幅值
保持间距比S/D=4不变,研究来流角度和约化速度对流动干涉作用的影响。角度越小错列圆柱就会越接近串联圆柱,反之,角度越大两圆柱的相对位置将趋于并联排列。因此当来流角度从小到大变化时,即可视为从串联圆柱向并联圆柱的逐渐过渡。图8为不同来流角度下错列两圆柱的频率比λ随约化速度的变化关系。观察图8发现,随着来流角度α的增大,圆柱的“锁振”开始位置出现前移倾向,且45°锁振区间相比孤立圆柱及其他双圆柱较为狭窄;在同一来流角度α时,上游圆柱与下游圆柱的“锁振”区间长度接近。
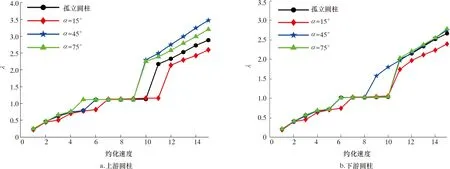
图8 不同来流角度下频率比随Ur的变化关系Fig.8 Variation of frequency ratio with reduced velocity at different flow angles
图9为不同来流角度α下错列圆柱的涡激振动响应随约化速度的变化关系。
由图9可以看出,α=15°时错列两圆柱的幅值显著大于孤立圆柱和其他来流角度时的数值。此外下游圆柱的振幅最终保持在0.28D附近,远远大于上游圆柱。不同来流角度下错列两圆柱的顺流向振幅随约化速度的增加持续增大,各条振幅曲线相近,且与孤立圆柱差别不大,因此判断错列圆柱来流角的改变对顺流向平均振幅的影响比横流向振幅的影响小。

图9 圆柱涡激振动响应随Ur的变化关系Fig.9 Variation of vortex-induced vibration response of cylinder with reduced velocity
3.2.2 圆柱运动轨迹
圆柱运动的轨迹如图10所示。由图10可知:当来流角度α=15°时,错列两圆柱的运动轨迹差异显著,上游圆柱的运动轨迹构成较为简单,下游圆柱则以非周期性运动为主,轨迹较为杂乱且相互重合,说明此时下游圆柱所受的干涉影响较大;当来流角度α=45°时,圆柱运动的周期性有所改善,“8”字形轨迹开始出现,下游圆柱的运动轨迹逐渐清晰简单,原因是来流角度增大后受到上游圆柱流动干涉作用的影响明显降低;当来流角度α=75°时,错列两圆柱运动轨迹的周期性进一步提升,“8”字形轨迹占据主导,上游、下游圆柱的运动轨迹愈发接近,并显现出并联两圆柱的轨迹对称特性。
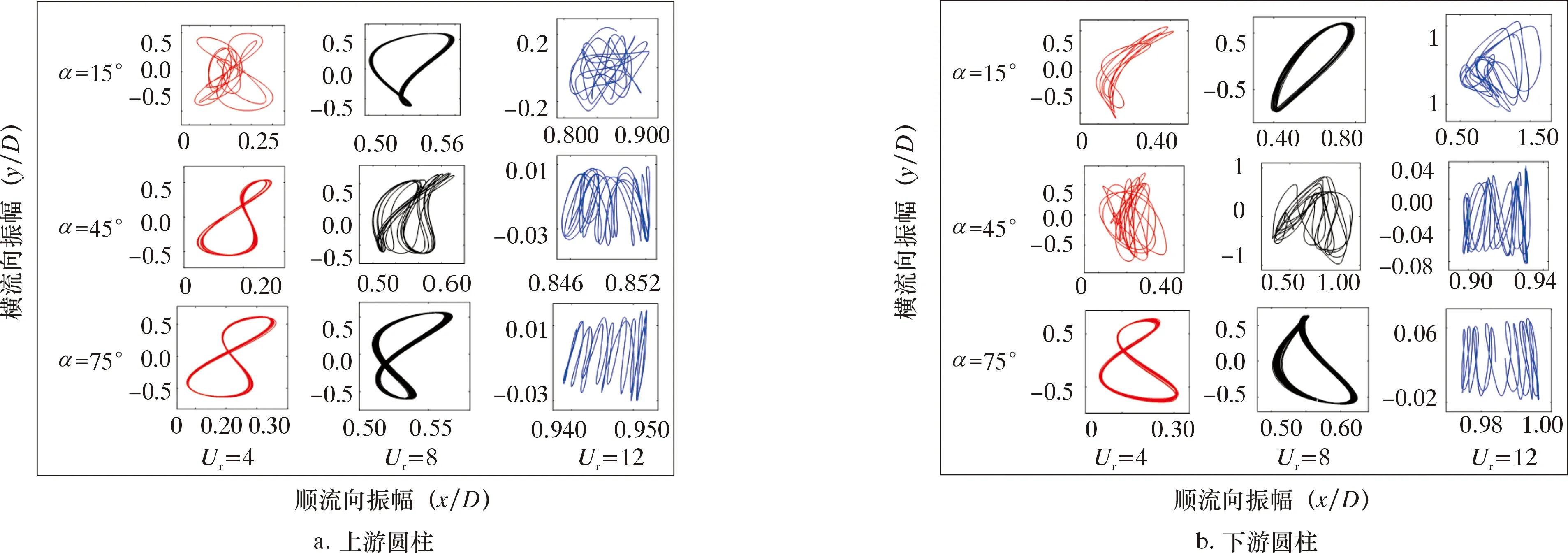
图10 两圆柱的运动轨迹(间距比不变)Fig.10 Kinematic trajectories of double cylinders (at constant spacing ratio)
3.2.3 流场分析
图11为不同来流角度下错列两圆柱的尾涡模态随约化速度的变化关系。由图11可知:当来流角度α=15°时,下游圆柱处于上游圆柱的尾流区中,两圆柱漩涡产生干扰,漩涡结构显得比较复杂;随着来流角度变大,下游圆柱逐渐脱离上游圆柱的尾流区,两圆柱的尾涡模态也变得简单、规则,从单一涡街模式变化为双涡街模式;当进入高约化速度且来流角度α=15°时,上游圆柱的两个剪切层并没有形成漩涡脱落,但由于上游圆柱对下游圆柱的干涉作用,推迟了下游圆柱的游涡脱落,这也与下游圆柱横向振幅受到限制逐渐减小和上、下游圆柱频率比逐渐接近的现象相对应;而随着来流角度增大,上、下游圆柱脱落的漩涡不再相互干扰,各自后方出现规则的涡街,呈现出与并联圆柱接近的“同向同步”模态。
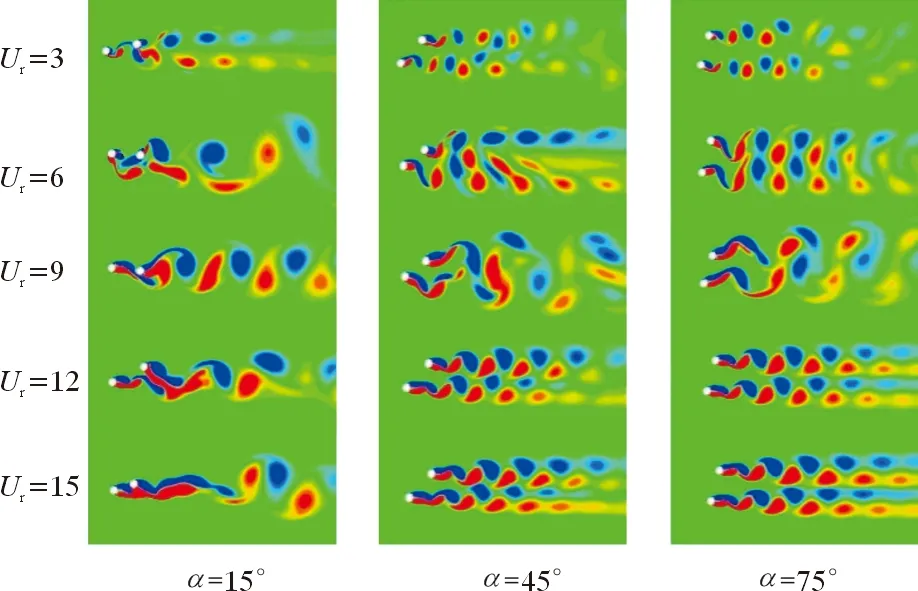
图11 不同来流角度下尾涡模态随Ur的变化Fig.11 Variation of trailing vortex mode with reduced velocity at different flow angles
4 结 论
(1)当间距比和来流角度较小时,错列两圆柱的流动干涉作用较为强烈,两圆柱的运动轨迹较为杂乱;随着间距比和来流角度的增大,圆柱的运动轨迹逐渐变得规则,两圆柱轨迹间的差异越来越小,上游圆柱和下游圆柱的运动轨迹将慢慢趋于一致。
(2)在间距比S/D=3时,流体与圆柱之间的耦合作用非常强烈,不能在圆柱后方形成规则脱落的漩涡;在高约化速度下,与其他间距比相比,下游圆柱受到上游圆柱尾涡脱落的影响更大,在横流向产生更大的振幅;下游圆柱也对上游圆柱产生“抑制”,使上游圆柱的尾涡变得细长。
(3)当来流角度α=15°时,上游圆柱的2个剪切层并没有形成漩涡脱落,由于上游圆柱对下游圆柱的干涉作用,推迟了下游圆柱的涡脱落,这也与下游圆柱横向振幅受到限制逐渐减小和上、下游圆柱频率比逐渐接近的现象相对应。
