基于DE-SVM的风电机组高速轴承故障诊断
2022-10-13叶凯黄雪梅张磊安范治达
叶凯,黄雪梅,张磊安,范治达
(山东理工大学机械工程学院,山东淄博 255000)
0 前言
随着风电装机容量的不断攀升,降低运维成本成为迫切需求。风电机组通常工作于恶劣的环境中,运行工况多变。作为风机传动链中关键部件的高速轴承长期处于交变载荷作用下,易发生故障,并且传动链故障造成的停机时间最长、发电量损失最多,造成的损失较为严重。据统计,陆上风电场运维成本高达总收入的15%~20%,海上风电场甚至高达30%~35%,运维成本高居不下。因此,从降低运维成本以及安全性方面考虑,有效实现风电机组故障诊断具有重要意义。
风电机组高速轴承的振动信号具有非线性、非平稳性的特征,故障诊断较困难,需要选取合适的故障诊断模型。支持向量机(Support Vector Machine,SVM)是一种基于统计学的分类模型,能有效解决小样本、高维数、非线性等问题,适应性和分类能力优秀,在故障诊断方面有较好的表现,已成功应用在机械故障诊断领域。研究表明,SVM模型分类能力受惩罚因子和核函数参数影响巨大,而参数的选取没有统一的标准和理论,一般凭借经验或利用交叉验证法通过大量实验进行确定,这就造成了选取的参数不一定最优,进而影响整个模型的分类能力。
综上所述,针对风电机组高速轴承故障诊断困难以及SVM模型参数选择问题,本文作者提出一种差分进化算法改进支持向量机(Differential Evolution-Support Vector Machine,DE-SVM)的风机高速轴承故障诊断方法。首先,使用集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)对采集信号进行降噪处理,得到若干本征模态函数(Intrinsic Mode Functions,IMFs),提取其能量特征构成SVM模型的输入特征集;然后,利用差分进化算法(Differential Evolution,DE)对SVM关键参数和进行寻优,构建DE-SVM分类模型;最后,将测试数据输入到优化后的SVM模型中,进行轴承的故障诊断和识别。
1 基本理论
1.1 SVM理论
支持向量机是VAPNIK等人提出的一种机器学习算法,其基本思想:对于线性问题,构造一个最优超平面对目标问题进行求解;对于非线性问题,一般使用适当的核函数将输入空间特征信息映射到一个高维特征空间,再利用线性方法在高维特征空间中求解问题。
对于轴承故障诊断问题,应抽象为非线性问题。设样本集为{(,),(,),…,(,)}∈(×),其中,∈⊂为输入向量,={-1,1}为对应的输出值,=1,2,…,,为训练样本数,为样本空间维数。
目标函数的对偶问题为
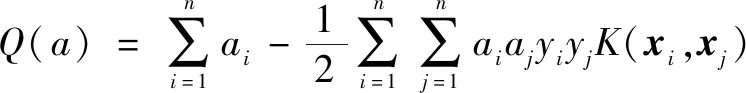
0≤≤,=1,2,…,
(1)
式中:(,)表示核函数;为惩罚因子。
相应的最优分类函数变为
()=sgn{(·)+}=
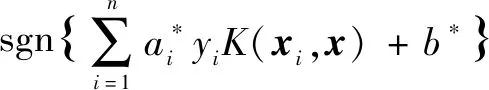
(2)
SVM处理非线性问题最关键的是核函数的设置,包括核函数种类的选择以及核参数的确定。文中选用径向基函数(Radial Basis Function,RBF)作为SVM的核函数。RBF具有优秀的非线性处理能力、较宽的收敛域,并且核参数单一,是理想的分类核函数。RBF核函数表示如下:
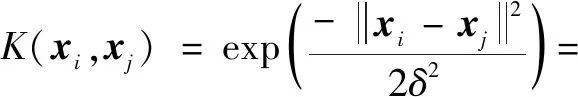
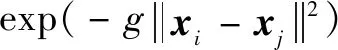
(3)
式中:为核函数内带宽;为核函数参数,=12。
综合上面各式,SVM性能受各种参数影响较大,尤其是受惩罚因子和核函数影响较大。惩罚因子表示对误差的容忍度,越大,表明对误差的容忍度越小,越容易过拟合;相反地,越小,越容易欠拟合,从而影响SVM的泛化能力。核函数是RBF核函数自带的唯一参数,它表示数据映射到新的特征空间后的分布,越大,支持向量越少;越小,支持向量越多。的大小影响SVM模型训练与预测的速度。
1.2 DE算法
DE算法是由STORN等人在遗传算法(Genetic Algorithm,GA)的基础上提出的一种基于群体差异的随机搜索算法。DE算法本质上是一种全局优化算法,用于求解非线性、多维空间中整体最优解。其基本思想:随机生成初始种群,经过随机差分和交叉操作得到中间种群;然后,利用贪婪策略在父代种群与当前种群之间进行选择与重组,最终得到新的种群;种群不断迭代,直至满足所设终止条件。DE算法的主要流程如下:
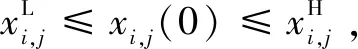
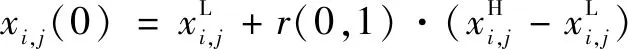
(4)
(2)变异。DE算法通过个体之间的差异进行差分变异操作,通过变异因子和差分向量对将要变异的个体进行合成。在第代个体中,随机选择3个个体,生成的变异向量为
(+1)=1()+·2,3()
(5)
其中:2,3()=2()-3(),为差分向量,≠≠≠;∈[0,2]为变异因子,表示差分向量的影响力大小。
(3)交叉。为增加种群多样性,同时保留父本有效信息,需要利用交叉算子对第代个体()和变异个体(+1)进行交叉操作,得到中间种群(+1):

(6)
其中:∈[0,1]为交叉算子,越大,算法收敛速度越快,越小,收敛速度越慢,但越有利于保持种群的多样性和提高全局搜索能力。
(4)选择。根据贪婪策略,在()和经过交叉操作后得到的(+1)个体之间进行选择,选择出适应度更高的作为下一代个体(+1)。

(7)
其中:为适应度函数。对于每个个体,(+1)要好于或持平于(),并不断进行变异、交叉、选择,直至满足终止条件。
2 DE-SVM模型
2.1 DE-SVM模型构建
本文作者基于DE算法良好的全局寻优能力、较快的收敛性以及参数设置较少等优点,选用DE算法进行参数寻优。以样本交叉验证平均得分最高为优化准则建立目标函数,对SVM的关键参数惩罚因子和核参数进行优化选择。DE-SVM模型构建流程如下:
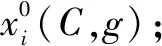
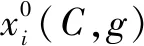
步骤3,进入下一代进化,=+1;

步骤5,输出最优个体即最优惩罚因子和核参数组合(,),将最优参数输入SVM模型中,DE-SVM模型构建完成。
DE-SVM模型参数寻优流程如图1所示。
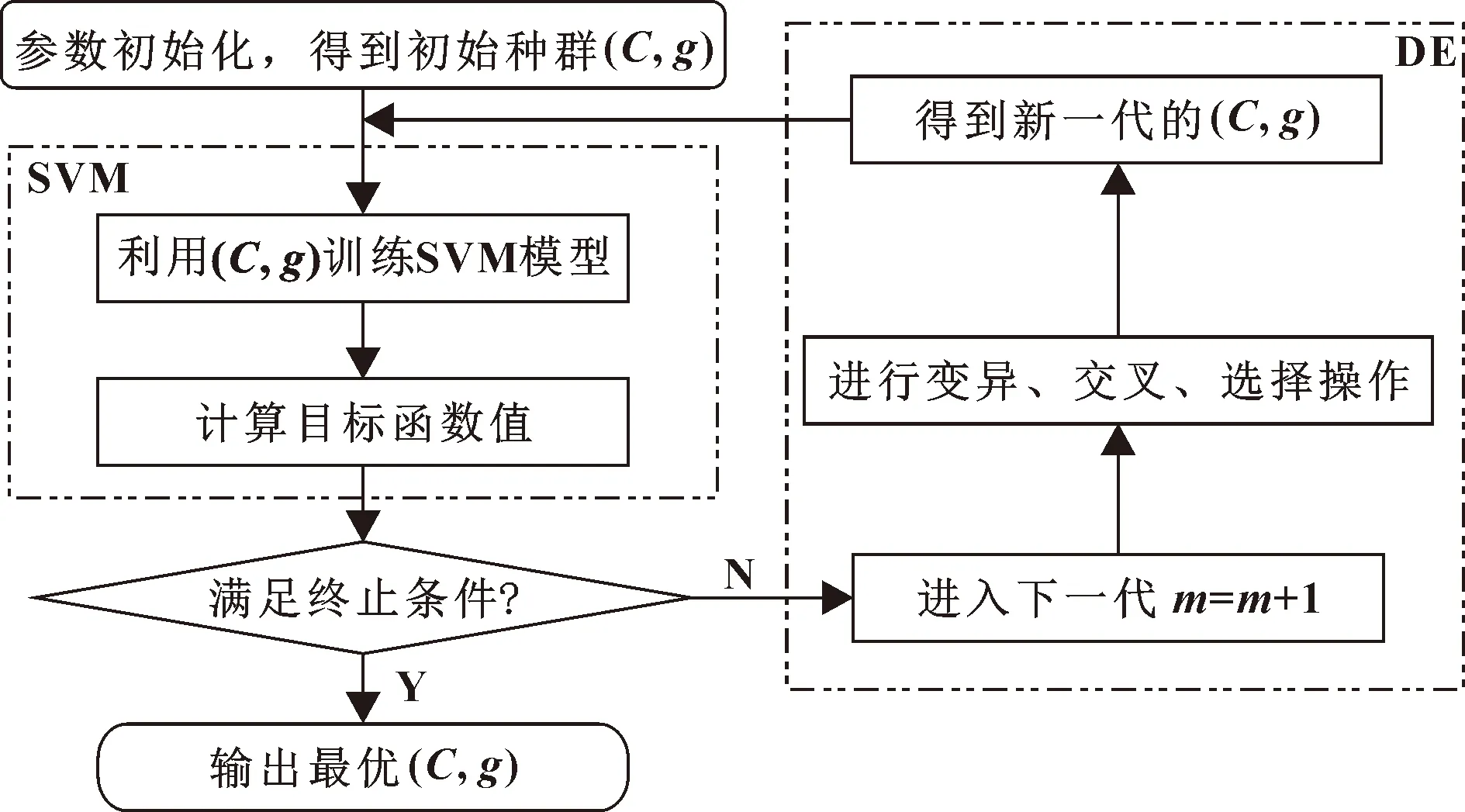
图1 DE-SVM寻优流程
2.2 DE-SVM参数选择
为取得良好的训练结果,需要对DE-SVM模型的关键参数进行选择,具体如下:
(1)种群规模。一般来说,种群规模越大多样性越多,越有利于寻得最优解,但也会增加计算难度,训练时间较长,文中选择=50;
(2)终止阈值。为保证精度,将终止阈值设为1×10;
(3)变异因子。变异因子又称缩放因子,用来决定差分向量的影响力,取值范围为[0,2],若该参数过小则差异性较小,容易早熟,陷入局部最优;如果过大,则收敛较慢;初始值一般取0.5,变异策略选择DE/rand/1/bin;
(4)交叉因子。取值范围为[0,1],取值越小越有利于保证种群多样性,同时收敛速度变慢;取值越大则收敛速度越快,但种群多样性降低,易发生早熟现象,文中取=0.2;
(5)SVM惩罚因子和核参数的范围。为保证多样性,参数取值范围为[2,2]。
3 实例分析
3.1 数据集设置
为验证DE-SVM算法在风电机组高速轴承实际故障诊断中的准确性和有效性,选用凯斯西储大学轴承实验中心提供的高速轴承振动数据进行实验分析。实验条件:采用电火花加工技术在滚动轴承外圈的6点钟方向、滚动体以及内圈预先布置单点故障,故障损伤直径为0.177 8 mm×0.279 4 mm,电机载荷1.47 kW(2马力),转速1 750 r/min,采样频率为12 000 Hz。在上述实验条件下分别采集正常状态、内圈故障、滚动体故障和外圈故障4种状态下的轴承振动信号,每种状态随机采集60组样本数据,共240组样本数据,每组样本数据长度为1 024,共245 760个样本数据。按照2∶1的比例将每种状态的数据随机划分为训练集和测试集,最终得到160组训练集、80组测试集。
3.2 故障特征提取
为有效地处理非线性、非平稳的信号以及提高后续故障识别的准确率,使用EEMD方法对采集到的滚动轴承振动数据进行降噪处理和提取故障特征。原始振动信号经EEMD分解后产生若干IMF分量和一个残余分量,对各IMF分量进行能量分析,计算每阶IMF分量的能量占比=,选取前7阶IMF分量,从而构建特征向量=[,,,,,,]。滚动轴承4种状态前7阶IMF分量能量占比如图2所示,160组训练集数据经EEMD分解之后的能量特征分布如图3所示。

图2 滚动轴承4种状态下前7阶IMF分量能量占比
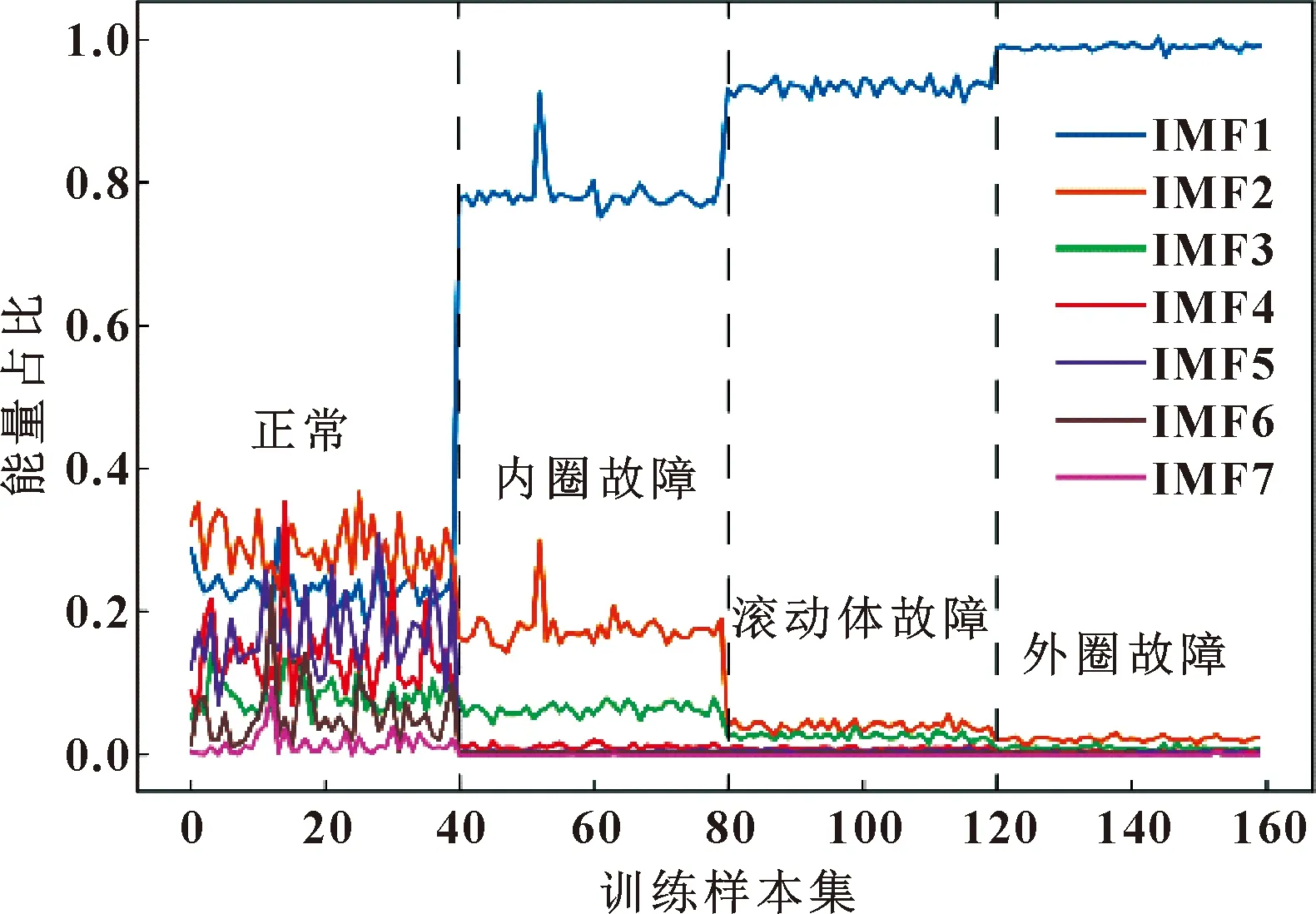
图3 训练集4种状态IMF能量分布
3.3 故障诊断分析
在上述故障特征提取的基础上对特征向量进行标准化处理并标记轴承故障类型,设置类别标签1、2、3、4,分别代表滚动轴承的正常无故障、内圈故障、滚动体故障和外圈故障4种状态。表1所示为部分样本数据。将训练集特征向量分别输入到经典SVM、遗传算法优化的支持向量机(GA-SVM)和文中所提的DE-SVM故障诊断模型中,进行分类器的训练拟合。3种SVM模型均采用RBF核函数,经典SVM采用工具箱默认参数,GA-SVM以及DE-SVM模型均使用相应的智能算法进行参数寻优,并根据寻优结果对分类器进行参数设置,完成模型的训练。其中,DE-SVM模型具体参数的选择参考第2.2节内容。最后,将80组测试集数据分别输入到训练完成的3种模型中进行验证,得出分类准确率。DE-SVM优化结果如图4所示,表2所示为3种算法比较结果。
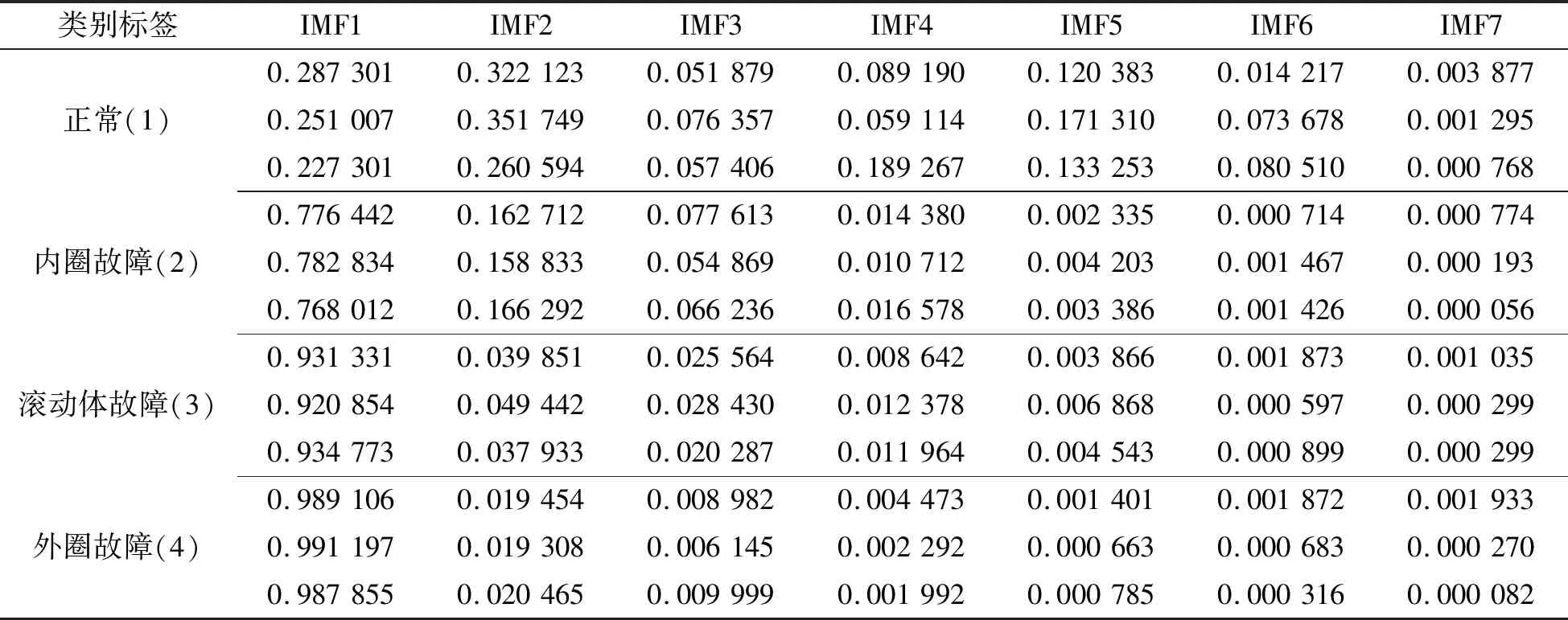
表1 部分训练样本数据

图4 DE-SVM优化结果
由表2可知:经典SVM对于正常状态、内圈故障的识别正确率为100%;对于滚动体故障20组数据正确识别出19组,识别准确率分别为95%;对于外圈故障20组数据正确识别出18组,识别准确率为90%,总体识别率为96.25%。GA-SVM和DE-SVM对于测试集的识别率均为100%,但DE-SVM训练用时更短,更快到达收敛,效果更好。由此可见,基于DE-SVM的故障诊断方法能够实现对风电机组传动链轴承故障的分类识别,具有较高的准确率。

表2 3种模型故障诊断结果
4 结论
(1)提出了一种基于DE-SVM的风机传动链轴承故障诊断方法。为减小SVM参数选择的主观性以及提高SVM的分类性能,采用DE算法对SVM模型的惩罚因子和核函数进行智能寻优。
(2)利用风电机组高速轴承数据进行分析,对DE-SVM故障诊断模型进行测试。结果表明:所提方法故障识别正确率达到了100%,识别能力较强,验证了该方法的有效性和准确性,为风电机组传动链轴承的故障诊断提供了新思路。
