潜在类别混合模型及其在纵向数据轨迹分析中的应用*
2022-10-12武振宇郑雪莹
殷 畅 武振宇 郑雪莹△
【提 要】 目的 介绍潜在类别混合模型及其在纵向数据轨迹分析中的应用。方法 以一项限制能量摄入的随机对照临床试验为例,应用潜在类别混合模型进行轨迹分析,结合贝叶斯信息准则、平均后验概率及高后验概率个体所占比例判断最佳轨迹数目及形状。结果 四组三次模型最优,人群分为四类减重模式:高体重快速减重组、低体重快速减重组、高体重缓慢减重组及对照组。结论 潜在类别混合模型既能识别群体中的异质性,又能考虑到类别内个体发展轨迹,有望广泛应用于纵向数据的处理分析。
流行病学研究经常关注某指标随时间变化的情况,并对该指标在不同时间点进行测量,由此得到的每个研究对象在不同时间点的测量值集合称为纵向数据[1]。与分析群体平均值或随访数据与基线数据的差值相比,分析数据纵向变化特征更能反映研究指标的发生发展状况,从而为寻找疾病控制的敏感期提供科学依据。处理纵向数据常用的方法有混合效应模型、广义估计方程、多水平模型、重复测量设计的方差分析等[2],可拟合研究指标随时间变化轨迹,描述发展趋势。而上述方法均假定研究对象的发展具有同质性,即群体内的所有个体遵循相似的发展规律,这一假设在现实中难以满足。如群体内有潜在的亚组在不同时期存在不同的变化模式,采用前述方法难以识别。
轨迹分析是流行病学领域新兴的一种分析方法。它根据个体测量的纵向数据,将其划分为具有不同发展模式的潜在类别,从而更好地描述随时间推移研究指标在个体内和个体间的变异性和模式[3]。常用于纵向数据的轨迹分析模型有以下三种:潜在转变分析(latent transition analysis,LTA)、基于组的轨迹模型(group-based trajectory models,GBTM)和潜在类别混合模型(latent class mixed model,LCMM)。三者均假设总体中存在有限个未观测到的具有相似发展模式的潜在类。LTA用于多分类变量的纵向数据分析,GBTM和LCMM可兼顾分类变量与连续型变量[3]。在轨迹分析中,将固定效应定义为每个潜类别的平均参数(截距和斜率),随机效应则表示个体参数与类平均参数的差异。GBTM假设不同类别间的固定效应不同,类别内的个体有相同的固定效应;LCMM则是GBTM的更一般形式:不同类别间的固定效应不同,类别内个体在固定效应相同的基础上还有不同的随机效应。相较于LTA与GBTM,LCMM兼顾类别间的异质性和类别内的个体效应,拟合更为准确。近年来,国内学者用轨迹分析方法探究纵向队列中研究对象身体质量指数[4-8]、血压[9-10]、肿瘤标志物[11-12]、生活质量[13]等重复测量指标的潜在发展轨迹,并分析不同轨迹与相应结局的关联。本文对LCMM进行介绍,并结合实例说明其应用,为相关专业人员提供参考。
原理与方法
1.基本思想与模型概述
LCMM基于潜变量分析(latent variable analysis)和增长混合模型(growth mixed model,GMM)。假设群体中有若干不可观测到的潜在类别(定义为分组变量),计算个体属于不同类别的概率,实现对群体的分组。对纵向数据部分的处理则基于GMM:类别间有不同的固定效应,类别内个体之间有随机效应[14]。因此,LCMM可以在考虑类别内个体差异的基础上估计固定效应,进而拟合出不同轨迹组的增长曲线。
基于潜变量分析,可根据研究对象属于各个潜在类别的概率,将有相似发展模式的个体归为一类。假设N个研究对象有G个异质的潜在类别,每个研究对象i有且仅有一个归属类别g(g=1,…,G)。用离散随机变量ci=g(g=1,…,G)定义研究对象i属于类别g,其概率πig可用包含协变量Xci的多项式logistic回归模型描述:
(1)
其中ξ0g是类别g的截距项,ξ1g是与协变量Xci相关的类特定参数[14]。
基于GMM,可估计类特定的固定效应及类别内个体的随机效应。以高斯分布的变量为例,类别g中的个体i在时刻j的测量值Yij可以表示为:
Yij|ci=g=XL1i(tij)Tβ+XL2i(tij)Tυg+Zi(tij)Tμig+ωi(tij)+ij
(2)
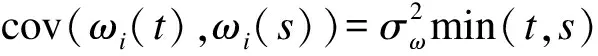
2.参数估计与分析步骤
LCMM采用最大似然法对参数进行估计,并用迭代MarQuardt算法获得最优解。该方法受初始值影响较大,在分析过程中需要尝试设置不同初始值来避免模型获得局部最优解而收敛[14]。
在应用LCMM前可结合专业背景及先验知识判断总体中异质性的存在。在此之后,通常需要遍历公式(2)中协变量XL1、XL2和Z的线性、二次和三次形式,每种形式分别拟合1~6组。为了确定最佳的轨迹数目和形状,采用以下标准进行筛选和判断:(1)贝叶斯信息准则(Bayesian information criterion,BIC)越低越好;(2)各类别平均后验概率大于0.7;(3)各类别中高后验概率(大于0.7)的个体占比超过65%。
常用R软件中的LCMM Package进行分析。LCMM Package中包含hlme、lcmm、multlcmm、jointlcmm等主要函数。hlme函数用于拟合潜在类别线性混合模型;lcmm在hlme的基础上增加了link函数,将可分析数据类型扩展到非高斯分布的变量;multlcmm为多变量分析函数;jointlcmm则将潜在类别混合模型与生存模型结合起来[14]。使用者可根据数据类型选择函数,本文以lcmm函数为例进行结果展示。
实例研究
1.数据来源
本研究数据来源于2011-2013年间能量摄入限制影响综合评估(comprehensive assessment of long-term effects of reducing intake of energy,CALERIE)的二期研究。它是一项多中心随机对照试验,也是第一个专门关注人类持续能量摄入限制(calorie restriction,CR)影响的研究。CALERIE试验对生理、心理、生活质量和认知功能进行全面评估,证明了人类持续CR(至少两年)的可行性和对长寿、心血管及代谢相关疾病的有利影响。CALERIE共招募了220名非肥胖健康研究对象,按照2∶1的比例随机分配至能量摄入限制(calorie restriction,CR)组(n=145)和随意饮食(ad libitum diet,AL)组(n=75),限制组两年间每日能源摄入量相对基线水平减少25%,对照组随意饮食。分别在干预开始后的第1,3,6,9,12,18,24个月测量体重[15]。在实际数据分析中,按照一定纳入排除标准(至少有基线数据、3~6个月之间的一次测量数据、12~24个月之间的一次测量数据),共纳入研究对象200人。其中男性60名,女性140名。
2.统计分析
用LCMM识别体重变化的不同发展模式,体重变化轨迹设置为随访时间的多项式函数。遍历了多项式函数的线性、二次和三次形式,考虑到研究人群数量不多,为了避免某一潜在类别人数占比过低,每种形式分别拟合1~5组。以1组三次的模型参数作为起始值,按照前述标准筛选最优模型。采用LCMM package(版本1.9.3)中的“lcmm”函数拟合模型,软件为R 4.1.0。
3.结果
志愿者以白种人为主,占总人数的77%;其次为黑种人(12.5%),亚裔(6.5%)及其他(4%)。基线平均身高为168.71cm,平均年龄为38.16岁。
表1为LCMM模型拟合结果。结合前述判断标准,4组三次模型为最佳模型,即:

表1 潜在类别混合模型(LCMM)拟合过程
Y(ij|ci=g)=(υ0g+μ0ig)+(υ1g+μ1ig)time+(υ2g+μ2ig)time2+(υ3g+μ3ig)time3+ij
其中,Y为高斯纵向结果体重(单位:千克),time为随访时间(单位:月),υ=(υ0g,υ1g,υ2g,υ3g)为类别g的固定效应系数,μ=(μ0ig,μ1ig,μ2ig,μ3ig)为类别g中个体i的随机效应系数,ij为随机误差。
图1所示为最优模型中不同亚组体重变化的轨迹曲线。根据体重的水平和变化速度,四个轨迹组分别命名为:高体重快速减重组(24%)、低体重快速减重组(42%)、高体重缓慢减重组(2.5%)和对照组(31.5%)。高体重快速减重组(n=48)平均从77kg开始,六个月快速减重8kg,之后维持不变,在CR后14个月开始产生较少的体重回涨,之后维持不变。在能量摄入限制后,低体重快速减重组(n=84)平均从68kg开始,六个月快速减重6kg,之后维持不变,后续变化与高体重快速减重组类似。高体重缓慢减重组(n=5)平均从80kg开始缓慢减重,在18个月之后体重减少约10kg,之后开始有反弹的回涨趋势。但因高体重受试者人数较少,能量摄入限制后的体重变化轨迹有待进一步验证。对照组(n=63)体重平均变化幅度很小,未进行能量摄入的干涉,为CALERIE实验的对照组。缓慢减重组在CR开始时体重下降速度较缓,但在长时间坚持后也能达到和快速减重组同样的效果。持续性25%能量摄入限制的效果不因减重模式不同而不同。
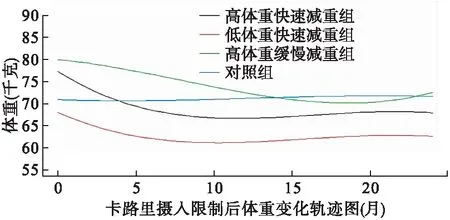
图1 体重变化轨迹分组
CALERIE试验有关的既往研究采用重复测量协方差分析的方法,认为相较对照组而言,限制组的核心体温并无显著变化,静息代谢率仅在一年内有所下降[16];骨密度变化微小,与所降低体重相符[17];男性去脂体重下降百分比显著高于女性[18];对睡眠质量无影响[17]。在轨迹分组的基础上拟合混合效应模型,纳入性别、年龄为协变量进行分析,发现四组之间核心体温无明显差异,而低体重快速减重组调整后的静息代谢率显著低于其他三组,这可能与体重基数小有关;高体重快速减重组、低体重快速减重组和对照组之间的去脂体重两两都有差异,可能因为低体重快速减重组的男性占比(15.48%)显著低于另外两组(高体重快速减重组56.25%,对照组28.57%);四组之间的骨密度、睡眠质量均无明显差异。因此,保证营养足够的前提下,25%能量摄入限制是安全无害的,不同的减重模式并不影响这一结论。
讨 论
LCMM假设已知的总体中含有限个未被观测到的潜在类别。不同类别之间有不同的发生发展模式,同一类别内的个体是相似的。相较常用的纵向数据处理方法,LCMM既能捕捉人群中不同潜在类别的异质性,又考虑到类别内个体的随机效应,从而更为准确地刻画并描述生长曲线。在使用LCMM分析数据前,应该考虑数据缺失的情况。有模拟研究表明,随机缺失情况下对结果的影响不大,非随机缺失的数据应尽量降低其缺失率[19]。LCMM Package默认删除缺失的观测,同时假设用GMM模型拟合个体纵向发展趋势时数据为随机缺失(missing at random)[20]。因此,在分析数据前应根据研究目的与数据质量进行合理的筛选或插补。
除了遍历的方法,Hannah Lennon开发了轨迹分析的八步法框架:先确认最佳组数,再确定多项式的形状,最后进行敏感性分析[21]。该方法是一种渐进式建模法,最终模型的构建建立在每一步的合理与恰当上,要求研究者对数据本身和研究背景充分掌握,且确保建模过程中每一步的有效性。而LCMM的一些参数设置具有主观性,设置不恰当会改变最终的分析结果。因此,探索性的遍历法在可操作性与灵活性方面更具优势。分析过程中,前述的判别准则并不是唯一的,一些研究也会考虑熵(entropy)、赤池信息准则(akaike information criterion,AIC)、对数似然比等作为选择最佳轨迹数目及形状的依据[22]。
流行病学研究中,分出潜在类别并不是终点。很多研究会继续探究影响轨迹分组的预测因素;或是将分组作为自变量,纳入协变量后分析其与结局指标之间的联系,常用Cox模型(生存数据)、logistic回归模型等。有的研究根据个体发展的轨迹参数,探讨疾病发生发展过程的敏感期,为疾病控制提供科学依据;还可以识别特殊的亚群,更好地探究病因学关联[21]。
综上所述,LCMM能更加准确地拟合群体中个体的变化轨迹,又能在群体中找出不可观测的潜在类别。有望在队列研究等有随访的纵向数据分析中广泛应用。目前并没有统一的使用及汇报规范,因此,应用时须充分了解其原理、条件和注意事项,合理解释结果。
