Ce3+/Eu2+掺杂无机发光材料构效关系与唯象理论

王淑欣，宋 振，刘泉林

（北京科技大学 材料科学与工程学院，北京 100083）

1 引 言

Ce3+/Eu2+掺杂无机发光材料在照明、显示、监测、示踪、防伪以及信息存储等领域具有重要应用。其中荧光粉转换发光二极管（pc-LED）以其发光效率高、体积小、全固态以及耐久性好等优异性能广泛应用于照明工业和液晶显示背光源领域[1-4]。源于Ce3+/Eu2+离子的发光跃迁是宇称允许的f-d电偶极跃迁，具有高效吸收和高效发射的优点；其激发能量取决于Ce3+/Eu2+激活剂离子的4f和5d能级之间的能量差。4f轨道的能级由于受到5s25p6壳层的屏蔽作用，其能量受外界环境的影响较小，基本不随基质材料的改变而改变。与4f轨道不同，5d轨道处于外层，其能级能量受基质晶体结构和激活剂所处的局域结构的影响较大。共价键效应、晶体场劈裂和电声子耦合作用可以有效调控其激发光谱和发射光谱，为基于组分-结构-性能的构效关系设计新型荧光粉提供理论依据和可行性[5-7]。另外，Ce3+/Eu2+掺杂LED荧光粉的发光性能还取决于其电子结构[8]，即稀土离子和基质材料的能级/能带结构。

作为pc-LED实用的发光材料，应满足以下要求：（1）具备和LED芯片发射光谱匹配的激发光谱；（2）合适的发射光谱；（3）高发光效率；（4）优异的发光热稳定性；（5）优异的化学稳定性[9-10]。在过去几十年中，研究人员成功研发出了一系列满足以上要求的荧光粉，得到了覆盖全部色调的商用白光发射LED器件。目前，商用LED荧光粉主要包括铝酸盐Y3（Al,Ga）5O12∶Ce3+、氮化物（Ca,Sr）-AlSiN3∶Eu2+、氧氮化物β-SiAlON∶Eu2+和（Ba,Sr）-Si2O2N2∶Eu2+、硅 酸 盐（Ba,Sr）2SiO4∶Eu2+和（Ba,Sr）3SiO5∶Eu2+等[11-16]。本 文 系 统 介 绍 了Ce3+/Eu2+掺杂无机发光材料的构效关系与唯象理论的研究进展，详细总结了基质材料组分、晶体结构、局域结构和电子结构对发光性能的影响规律。

2 Ce3+/Eu2+掺杂无机发光材料的构效关系与唯象理论

Ce3+/Eu2+掺杂无机发光材料的发光过程可以分为能量吸收、无辐射弛豫和辐射跃迁发光三个阶段：（1）当受到激发时，激活剂离子Ce3+/Eu2+吸收能量使得电子从4f基态跃迁至5d激发态；（2）由于5d电子和晶格声子发生耦合作用，部分激发能量以无辐射跃迁的形式散失，激发态弛豫到最低激发态；（3）弛豫后的5d激发态电子跃迁至4f基态发光[17]。因此，荧光粉的激发能量取决于Ce3+/Eu2+激活剂离子的4f和5d能级之间的能量差。基质对5d能级的影响通常可以使用质心移动εc和晶体场劈裂εcfs两个参量进行表征，如图1所示[18]。在基质材料中，由于共价键效应，电子间斥力减少，5d能级向低能方向移动；5个5d能级平均能量的下移称为质心移动εc。此外，根据激活剂离子占据的晶体格位的对称性，简并的5d能级最多可分裂为5个不同的5d态；晶体场劈裂εcfs则为最高5d能级和最低5d能级之间的能量差。质心移动εc和晶体场劈裂εcfs的整体效应导致5d和4f能级之间的能量差减小，直接决定了材料的激发光谱所处的位置和带宽。在已知激发谱的情况下，发射谱和峰位主要由电声子耦合和斯托克斯位移ΔS决定。稀土离子的电子在从激发态回到基态发光之前，会与晶格声子发生耦合使其部分激发能以非辐射跃迁形式散失，导致发射光相对于激发光红移。这种相同电子态间电子跃迁的吸收和发射能量的差值称为斯托克斯位移[19-20]。在过去几十年中，研究者们研发出了许多Ce3+/Eu2+掺杂的无机发光材料，并深入理解其构效关系。在理论方面，Dorenbos建立了一套完整的唯象理论，为理解、预测、设计和调控稀土掺杂无机发光材料的性能提供了重要的科学依据[5]。本节综述质心移动、晶体场劈裂、诱导效应、斯托克斯位移、发光效率和发光热猝灭以及电子结构等相关研究进展，系统总结Ce3+/Eu2+掺杂无机发光材料的构效关系与唯象理论。

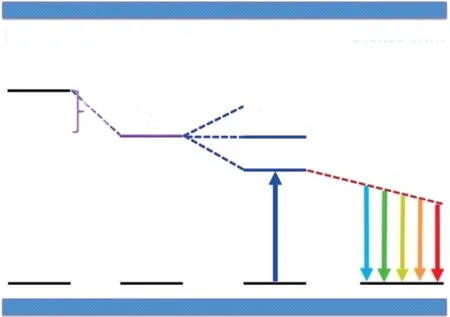
图1 Ce3+/Eu2+发光性能与配位环境之间的关系[8］Fig.1 The correlations between the luminescence property of Ce3+/Eu2+and the coordination environment[8］

2.1 电子云扩展效应或共价键效应——质心移动

基质中Ce3+/Eu2+5d能级的平均能量（质心）低于自由离子中5d能级的平均能量，平均能量降低的大小称为质心移动εc。质心移动通常被认为与电子云膨胀相关，称为电子云扩展效应或共价键效应，与5d轨道和阴离子p轨道的共价性密切相关。共价性使镧系阳离子的电子间平均距离增大，从而减少了库伦斥力，产生质心移动[21]。1980年，Morrison首次提出配位极化模型，强调5d电子和阴离子配位电子的交互作用对质心移动的重要作用[22]。在配位极化模型中，金属电子的瞬时位置使周围配体极化，极化的配体又作用于金属电子本身。这种自感电势减少了金属电子间的库伦排斥，从而导致电子能量质心位置降低，即质心移动。

为了进一步定量地理解和预测化合物中掺杂稀土离子的5d能级的质心移动，在共价模型和配位极化模型的基础上，Dorenbos提出一个新的参数，即光谱极化率αsp[23]。它综合了（1）配体极化、（2）共价性和（3）电子云扩展效应对质心移动的影响。假设，（1）总质心移动是每个阴离子单独贡献的结果的叠加；（2）只有最近邻阴离子对质心移动有显著贡献；（3）所有配体的极化率相同，则质心移动可表示为

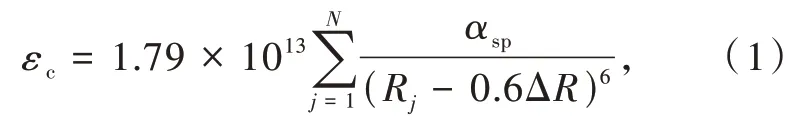
其中Rj（pm）是在未弛豫晶格中Ce3+到阴离子j的距离；求和为N个近邻配位阴离子配体的总和；ΔR≡RM-RLn，其中RM是被离子半径为RLn的镧系元素Ln取代的阳离子的离子半径；0.6ΔR是键长弛豫的估计值。该关系式表征了代表发光性能的光谱极化率、代表化合物结构的离子间距和代表成分的电负性之间的关系。此外，Dorenbos建立了光谱极化率αsp和平均阳离子电负性χav之间的相关关系：

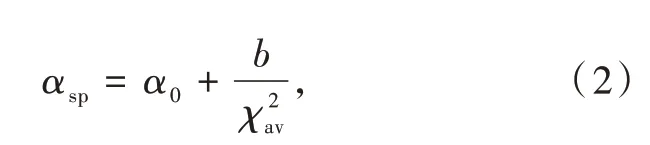
其中α0是极大χ情况下的极限极化率；b代表阴离子由于与金属键合而改变其极化率的敏感性。平均阳离子电负性χav定义为

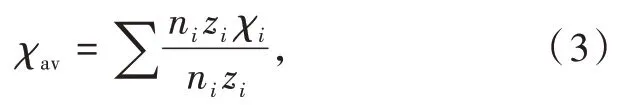
其中ni为化学式中带有电荷zi和电负性χi的阳离子的数量。

基于以上理论，Dorenbos采用统计分析方法，通过分析Ce3+掺杂氧化物和氟化物的光谱和结构数据，得到了光谱极化率αsp和平均阳离子电负性χav之间的定量关系，如图2（b）所示[24,26]。在氧化物中[23,26]：

图2 （a）卤化物和氧化物中Ce3+5d能级的质心移动[5］；（b）Ce3+掺杂氮化物、氧化物和氟化物中光谱极化率和平均阳离子电负性之间的相关关系[24］；（c）Ce3+掺杂氮化物荧光粉中光谱极化率αsp和平均阳离子电负性χav的相关关系的修正结果[25］。Fig.2（a）The centroid shift for Ce3+5d configuration in halides and oxide compounds[5］.（b）Spectroscopic polarizability against the inverse square of the average cation electronegativity in Ce3+doped nitrides，oxides，and fluorides[24］.（c）The revised correlation between the spectroscopic polarizability and the average cation electronegativity in Ce3+doped nitrides[25］.

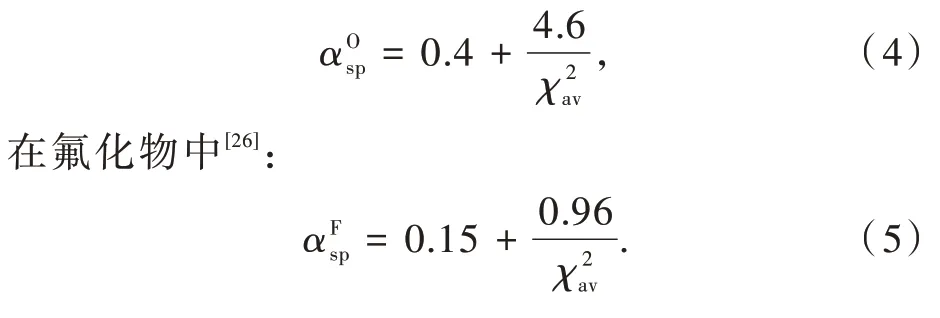
近几十年来，Ce3+/Eu2+掺杂氮化物发光材料由于其独特的发光性能以及在白光LED领域广泛的应用前景而备受关注。我们课题组研究了Ce3+掺杂氮化物中光谱极化率αsp和平均阳离子电负性χav之间的定量关系[24]。通过分析Ce3+掺杂氮化物的光谱和结构数据，得到了如图2（b）所示的定量关系。对比氟化物和氧化物，我们得到bF＜bO＜bN，这是由于阴离子与金属键合时电子云的极化程度按照由F到O到N的顺序依次增加。这一结果说明通过O代替F或N代替O可以得到更大的质心移动，实现发光材料的光谱红移。

荧光粉中Ce3+/Eu2+的配位结构对于研究其组分-结构-性能相关关系至关重要，然而很多化合物的配位结构数据在不同报道中相互矛盾。因此，我们课题组根据键价理论和配位多面体的稳定性提出了一套确定氮化物中阳离子配位数的统一标准[25]。在此基础上，通过分析Ce3+掺杂氮化物发光材料的光谱数据和结构数据，修正了光谱极化率和平均阳离子电负性之间的定量关系如下（图2（c））：

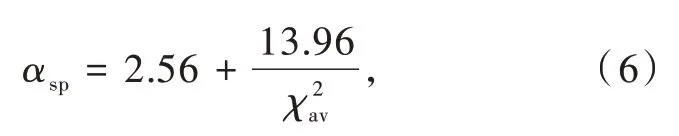
Dorenbos模型的建立为预测Ce3+/Eu2+掺杂无机发光材料的质心移动提供了理论依据，为基于材料组分和结构预测以及调控激发性能提供了参考和指导。

2.2 晶体场劈裂

Ce3+/Eu2+5d能级的晶体场劈裂εcfs拓宽了激发光谱，使Ce3+/Eu2+掺杂荧光粉可调控到被蓝光等低能辐射激发。晶体场劈裂由5d电子和阴离子配体之间的交互作用、泡利作用以及库伦作用共同引起。

Dorenbos通过分析六十多种Ce3+/Eu2+掺杂荧光粉（包括卤化物、氧化物、硫化物和硒化物）的光谱和结构数据，揭示了晶体场劈裂和Ce3+/Eu2+周围的配位环境之间的关系[27]。结果表明晶体场劈裂和激活剂离子的配位数、配位多面体的类型和尺寸密切相关，而与配位阴离子的种类无关。在Ce3+/Eu2+占据相同配位多面体的化合物中，晶体场劈裂可以表达为

其中βQpoly为常数，与配位体类型相关；Rav定义为

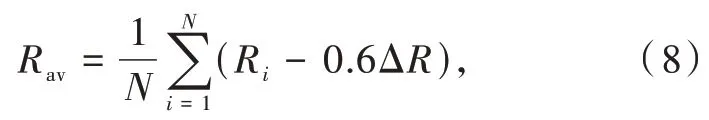
其中Ri是未弛豫晶格中镧系离子到N个配位阴离子的键长；ΔR≡RM-RLn，其中RM是被离子半径为RLn的镧系元素Ln取代的阳离子的离子半径；0.6ΔR是键长弛豫的估计值。通过分析拟合具有6配位八面体（Octa）、8配位六面体（Cubal）和12配位立方八面体（Cubo）的晶体结构的荧光粉的结构和光谱数据（图3（a）～（c）），Dorenbos得到了具有不同配位环境的荧光粉的βpoly。不同配位环境中的Ce3+和Eu2+的βpoly值具有相同的比值，即βocta∶βcubal∶βcubo=1∶0.89∶0.44；对于12配位的Eu2+，βocta为1.36×105eV·pm2。此外，通过进一步分析拟合得到了Ce3+和Eu2+晶体场劈裂之间的关系[28]：

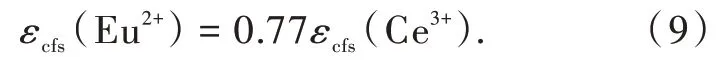
我们课题组进一步研究了Ce3+/Eu2+掺杂氮化物荧光粉中5d能级的晶体场劈裂与基质材料结构和组分之间的相关关系[6]。得到了晶体场劈裂与配位多面体的类型和尺寸的关系，如图3（d）、（e）所示。结果表明晶体场劈裂随着配位数的增加而减小。在配位数相同的情况下，晶体场劈裂εcfs与平均配位键长R-2av成正比。通过对比分析在相同氮化物中占据相同阳离子格位的Ce3+和Eu2+的晶体场劈裂数据，得到了线性相关关系

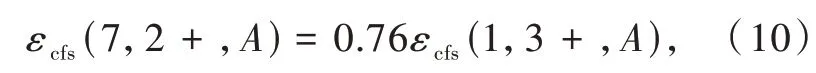
即在相同氮化物中占据相同阳离子格位的Eu2+的晶体场劈裂是Ce3+的0.76倍。Ce3+/Eu2+掺杂氮化物荧光粉的分析结果与Dorenbos在氟、氯、氧化物中得到的结论一致[28]，进一步证实晶体场劈裂主要取决于阳离子的配位多面体的类型和尺寸，与阴离子类型无关。晶体场劈裂与配位数密切相关，如图3（d）、（e）所示，因此，可预测具有CaAl-SiN3结构类型的MgAlSiN3化合物可产生大的晶体场劈裂。据此，我们设计并制备出了CaAlSiN3∶Mn2+荧光粉。Mn2+在八面体六配位场下的基态与第一激发态的能级差与晶体场强度负相关，这一特性与Cr3+相反。然而，目前报道的Mn2+的发光在可见的绿光-红光区。通过在Mg位置掺杂Mn2+，获得了具有宽带远红-近红外发射的氮化物发光材料MgAlSiN3∶Mn2+。发射峰位于754 nm，半峰宽约150 nm。这为研发新型宽带近红外发光材料提供了一种策略[29]。

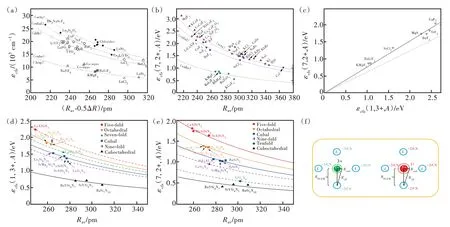
图3 卤化物、氧化物、硫化物和硒化物荧光粉中Ce3+（a）和Eu2+（b）5d能级的晶体场劈裂，以及其相关关系（c）[5，27-28］；Ce3+（d）和Eu2+（e）掺杂氮化物的晶体场劈裂ecfs；（f）Ce3+和Eu2+的配位环境。L为F-、S2-、N3-等配体，CN为配位数，Rradi为中心离子的离子半径，RPCEM是配体和中心离子的平均距离，Reff是配体和中心离子的有效距离[6］。Fig.3 The crystal field splitting of the 5d configuration of Ce3+（a）[27］and Eu2+（b）[5］，and their correlation in phosphors including halide，oxide，sulfide，and selenide compounds（c）[28］.The crystal field splitting of the 5d configuration of Ce3+（d）and Eu2+（e）in nitride phosphors[6］.（f）Coordination environment of Ce3+/Eu2+.L is the ligand，F-，S2-，N3-and so on，CN is the coordination number，Rradi is the ionic radius of central ion，RPECM is the average distance between ligand and central ion，Reff is the effective distance between ligand and central ion[6］.

关于晶体场劈裂，可通过点电荷静电模型（PCEM）进行计算和解释。八面体、立方体和立方八面体配位多面体分别包含一个上下表面有0，2或6个配体的三棱柱和反三棱柱[30]。Görller-Walrand等提出晶体场参数B20和B40可以表达为

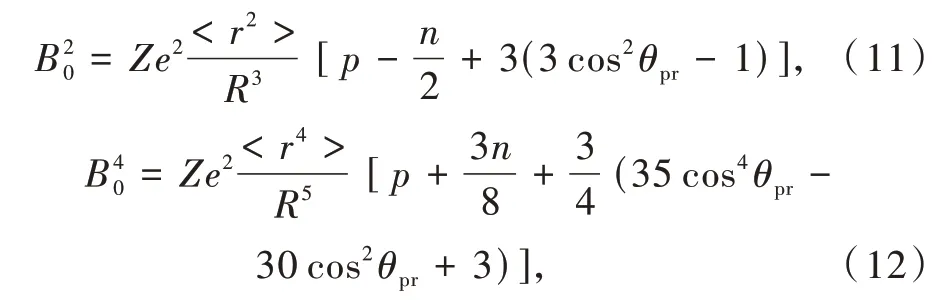
其中Z为配体电荷，R为键长，r为离子半径，P为三次对称轴平面的数量，n是垂直三次对称轴的平面数量。θpr是三次对称轴和从原点到6个棱柱顶点阴离子的矢量之间的夹角。括号中的表达式表示角部分Θkq，描述了阴离子的几何构型对晶体场参数的影响。八面体、立方体和立方八面体配位的Θ20约等于0，Θ40分别为-2.33，2.07，1.17，比值为1∶0.89∶0.5，和以上使用经验公式拟合得到的结论基本一致。

晶体场劈裂的大小与阴离子的类型无关，而主要取决于配位多面体的几何构型，即点电荷静电模型中的角部分Θkq。然而，根据Bkq的表达式可以看出Bkq和配位电荷Z成正比。即在点电荷静电模型中，晶体场劈裂应该和配位阴离子的电荷有关，这和使用经验公式分析拟合得到的结果相矛盾。我们课题组提出使用阴离子的有效电荷Z=Q/N（Q（Ce3+）=3，Q（Eu2+）=2）代替形式电荷Z（卤化物为1，硫化物和氧化物为2，氮化物为3）可以有效解释这一矛盾。图3（f）绘制了有效电荷概念示意图，其中N个配位离子分别携带Q/N个有效电荷。所以Bkq中的配位电荷Z与阴离子的类型无关，而是与Ce3+和Eu2+阳离子的电荷成比例。此外，Eu2+和Ce3+电价之比为2/3=0.67，根据点电荷静电模型，Eu2+5d能级晶体场劈裂应为Ce3+5d能级晶体场劈裂的0.67倍，这一数值与统计分析得到的0.76十分接近。因此,有效电荷的概念也可以在一定程度上帮助理解Eu2+的晶体场劈裂小于Ce3+的晶体场劈裂的原因[6]。

值得关注的是，晶体场劈裂不仅取决于发光中心与配体的距离r，还取决于配位多面体的几何构型，即角部分[31-32]。在晶体材料中，配位多面体相互之间通过共顶点、共棱或共面连接[33]。通过掺杂通常引起本身和相邻配位多面体形状和大小的协同变化，导致晶体场劈裂出现复杂的变化规律，比如在YAG∶Ce3+材料体系中[34-36]。深入理解这些变化规律，需要对局域结构和晶体场进行深入的分析。将质心移动与晶体场劈裂理论相结合，可以帮助预测和调控Ce3+/Eu2+掺杂的无机发光材料的吸收光谱和激发光谱。

2.3 诱导效应对电荷迁移带和fd跃迁发光的影响

Ce3+/Eu2+5d能级作为决定其发光性能的重要因素，主要取决于基质的组成和结构。5d能级的质心位置主要取决于电子云扩展效应的影响，即由材料整体的组成和平均结构决定。此外，局域结构也对5d能级的能量位置有重要影响。最近邻配位阴离子对5d能级的影响，即晶体场劈裂，广泛用于理解和预测材料的发光性能。然而，次近邻阳离子对5d能级能量的影响，即诱导效应，却很少被关注。如图4（a）所示，对于三元化合物TxMyXz，其中X为阴离子，T和M为阳离子。如果T电负性小于（或电正性大于）M，那么T较M来说更倾向于成为电子施主而提供电子，该电子会影响M—X键的电子云分布，即阴离子X更倾向于得到来自阳离子T的电子而不是阳离子M的电子，M—X键类型必定会发生一定程度的变化，这个现象被称之为诱导效应[37]。

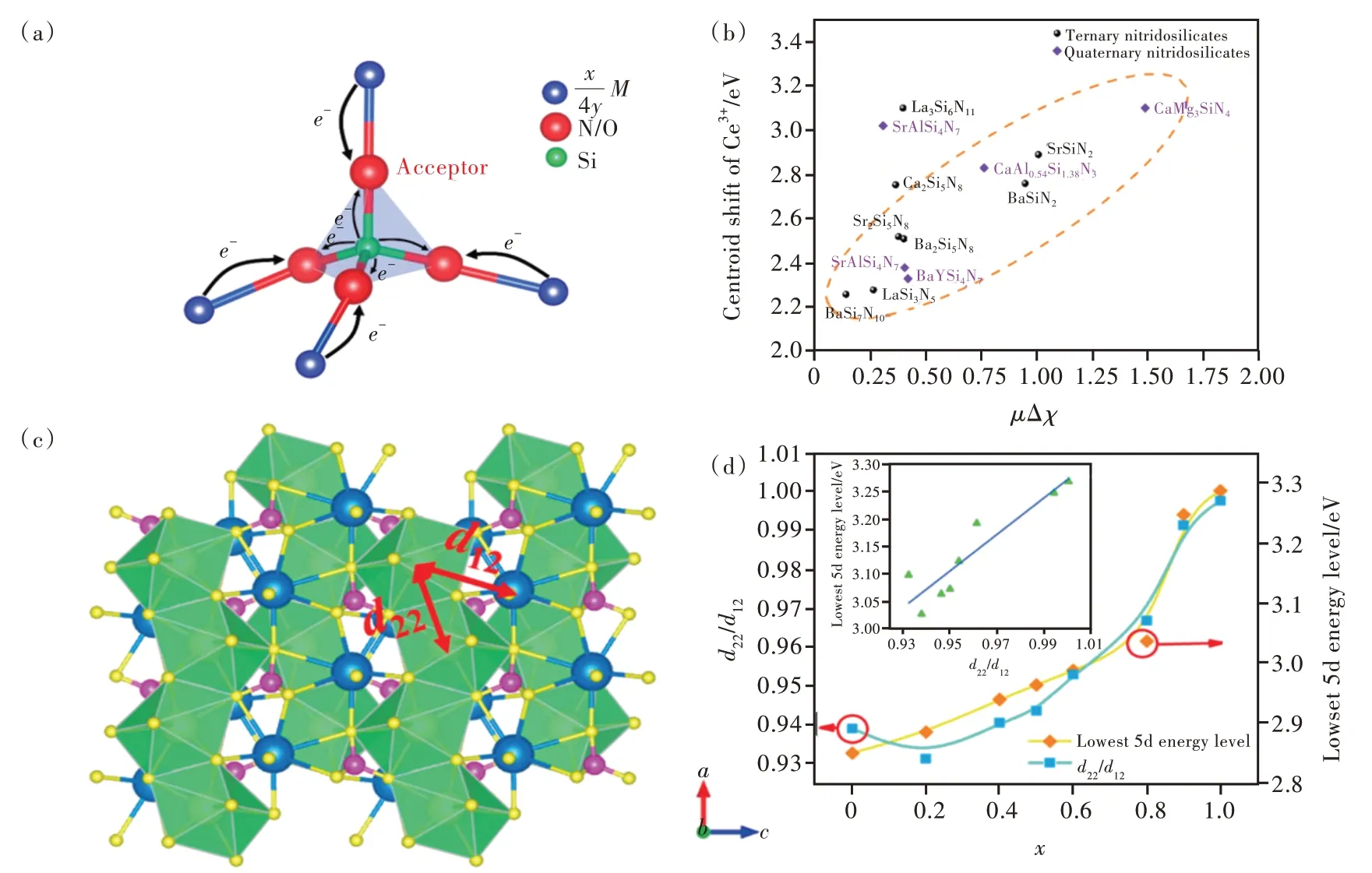
图4 （a）金属元素M的诱导效应机理图[40］；（b）三元/四元硅氮化合物中Ce3+5d能级质心移动εc和诱导因子μΔχ的关系[40］；（c）诱导效应：KxBa1.97-x（Si1-xPx）O4∶0.03Eu2+中Eu2+最低5d能级与d22/d12比值随x值的变化关系[43］。Fig.4（a）Schematic diagram of the inductive effect of M.The thickness of arrow represents the degree of ability of donating electrons[40］.（b）Centroid shift of 5d levels of Ce3+versus the inductive factor in（qua）ternary nitridosilcates[40］.（c）Inductive effect：lowest 5d energy level and the ratio of d22 to d12 as functions of the x values in KxBa1.97-x（Si1-xPx）O4∶0.03Eu2+[43］.

诱导效应在有机化合物中被广泛应用，随后Noll[38]首次引入到无机固体中用来解释硅酸盐中Si—O键 的 变 化。1992年，Etourneau等[37]采 用 诱导效应概念来解释无机化合物的包括氧化还原势、电导率、磁学性质、光学性质等的变化。2017年，Xiao等将诱导效应的概念引入至Ce3+/Eu2+掺杂 无 机 发 光 材 料 中，用 于 解 释K2（0.995-x）Na2xAl2B2O7∶0.01Eu2+的可调控发光性能。激发光谱分析显示Eu2+5d能级的质心移动随着x的增大而减小，Xiao等使用诱导效应对这一现象进行了解释[39]。2018年，我们课题组对硅氮/氧化合物中诱导效应对局域结构和发光性能的影响规律进行了系统研究[40-41]。

电负性是理解诱导效应的重要参量，Pauling将电负性描述为“分子中原子吸引电子到自身的能力”；Leach将电负性描述为元素的基本属性[42]。我们课题组从结构化学角度出发，采用统计学方法，通过研究上百种硅氮/氧化合物的晶体结构和光谱数据，提出了关键参数——诱导因子μΔχ，定量化研究了次近邻阳离子的诱导作用[39]。发现[SiN4]或[SiO4]四面体的加权平均键长以及Si原子加权平均键价与诱导因子呈明显线性关系。金属在硅氮化合物中的诱导效应要明显强于硅氧化合物。同时，发现Ce3+5d能级质心移动εc大小与诱导因子μΔχ正相关，如图4（b）所示。

诱导效应也可以用于理解分析电荷迁移带的变化规律[41]。稀土离子电偶极允许的跃迁分为两种：电荷迁移（Charge transfer,CT）跃迁和4fn-4fn-15d跃迁。前者像是从配体得到一个电子被还原，例如四价离子Ce4+、Pr4+和三价离子Sm3+、Eu3+、Yb3+倾向于得到电子变成相应三价和二价离子，光谱上表现为电荷迁移吸收带；而后者的4f-5d跃迁像是失去电子被氧化的过程，例如三价离子Ce3+、Pr3+和二价离子Eu2+、Sm2+、Yb2+倾向于变成相应的四价和三价离子，光谱上表现为4f-5d吸收带。在很多三价稀土离子掺杂的化合物中，三价稀土阳离子得到配位阴离子的电子而成为二价阳离子，光谱上表现为宽带吸收，称之为电荷迁移带。从诱导效应角度来看，如果稀土阳离子配位多面体外的次近邻阳离子的电负性不同，将影响阴离子的电荷分布，从而影响电荷迁移过程难易程度，在光谱上表现为电荷迁移带的红移或蓝移。反之，电荷迁移带的位置也必然反映出稀土离子局域结构环境。我们通过分析三价稀土离子掺杂无机固体的电荷迁移带以及晶体局域结构相关信息，研究了在电荷迁移过程中晶体局域结构的诱导作用，提出次近邻配位阳离子的两个重要诱导参数——电负性因子和离子半径因子，从而半定量化研究了次近邻阳离子通过诱导效应对稀土离子电荷迁移带的影响规律。通过将次近邻阳离子按照晶体学格位种类进行分类，讨论了一种、两种、三种以及更多种类次近邻阳离子发生改变时的电荷迁移带能量变化。研究发现，电荷迁移能与电负性呈负相关关系，而与离子半径呈正相关关系[36]。

诱导效应与最近邻阴离子和次近邻阳离子的距离和几何构型密切相关。例如，我们发现在KxBa1.97-x（Si1-xPx）O4∶0.03Eu2+固溶体中，Eu2+最低5d能级与d22/d12比值密切正相关，该现象可用诱导效应来解释[43]。当Eu2+取代了M2格位时，沿链方向的最近邻的阳离子之间的距离（d22=0.392 8 nm）小于链间两最近邻的阳离子的距离（d12=0.420 1 nm）。因此，最近邻的Ba更易于贡献出一个电子，并对Eu—O施加更多的电子压力，这就使得Eu—O的共价性有所上升。因此，沿链方向的5d轨道就会具有更低的能量，成为最低5d能级，并决定了最低激发带的位置。在KxBa1.97-x（Si1-xPx）O4∶0.03Eu2+中，随 着x值 的 增加，d22逐渐增加而d12逐渐减小，如图4（c）所示。因此，沿链方向形成的d轨道能量升高，引起激发 峰 的 蓝 移。对 于 端 元 成 分KBaPO4∶Eu2+，d22几乎等于d12，这就导致了链状效应的消失，最低激发峰也具有最大的蓝移[43]。

2.4 电声子耦合和斯托克斯位移

斯托克斯位移ΔS即为相同电子态间电子跃迁的吸收和发射能量的差值。基于晶体场劈裂和质心移动可以根据化合物的组分及结构预测荧光粉的激发谱位置，在此基础上结合斯托克斯位移则可以进一步预测荧光粉的发射谱位置。

对于Ce3+/Eu2+掺杂无机化合物，斯托克斯位移是最低5d能级和4f基态能级之间吸收和发射能量的差值。斯托克斯位移源于电声子耦合，可用位形坐标模型进行描述[38]，如图5所示。基于以下两个假设：（1）Born-Oppenheimer近似，即掺杂离子内电子转移的光学跃迁发生得很快以至于在跃迁过程中晶格不发生弛豫；（2）仅考虑一种晶格振动模式，呼吸振动模式。同时假设基态和激发态振动频率相同。因此，斯托克斯位移ΔS可表达为[44]

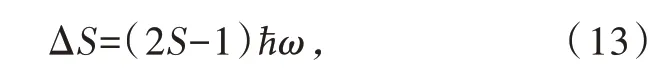
其中ћ为约化普朗克常数；ω为振动圆频率；ћω是连续振动能级之间的能量差，即为声子能量；无量纲黄昆因子S表示电子态和振动态的耦合程度，即电子-声子耦合程度。公式（13）广泛应用于Ce3+/Eu2+掺杂荧光粉的斯托克斯位移的计算和分析[20,45-46]，然而，近年来另一公式ΔS=2Sћω出现在一些研究报道中[47-48]。Jong等系统地研究了这一问题，发现这两个表达式都是近似正确的，实际的斯托克斯位移位于两个公式的计算结果之间[19]。Blasse等对电子-声子耦合程度进行了分类，定义S＜1为弱耦合，1＜S＜5为中耦合，S＞5为强耦合[49]。黄昆因子S的计算公式为：

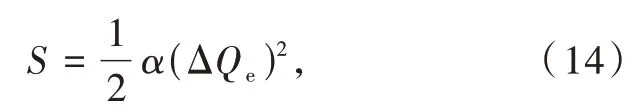
其中α=Mω/ћ，M为振动系统的约化质量。ΔQe为晶格弛豫；电子被激发到激发态时，电子云分布的改变致使核处于一个新的平衡位置，平衡位置的变化量称为晶格弛豫ΔQe，如图5所示[19,44]。晶格弛豫ΔQe取决于化合物中镧系离子替代的阳离子种类、配位阴离子种类以及局域结构。Blasse等报道在三个正硼酸盐中，镧系离子所替代的阳离子越大，斯托克斯位移越大[50]。此外，如公式（13）所示，声子能量ћω和斯托克斯位移正相关。文献报道声子能量在卤化物体系中按氟化物（～350 cm-1）到氯化物（～260 cm-1）到溴化物（～200 cm-1）的顺序依次减小[51]。氧化物（～600 cm-1）比硫化物（～270 cm-1）具有更大的声子能量，硒化物（150 cm-1）声子能量最小[52]。这些结果表明晶格振动频率ω按照从氧化物到硫化物到硒化物的顺序依次降低。在卤化物体系中按照从氟化物到氯化物到溴化物的顺序依次降低。这是由于原子质量增加，原子半径增加，电负性降低以及键合强度变弱，从而晶格振动频率降低。

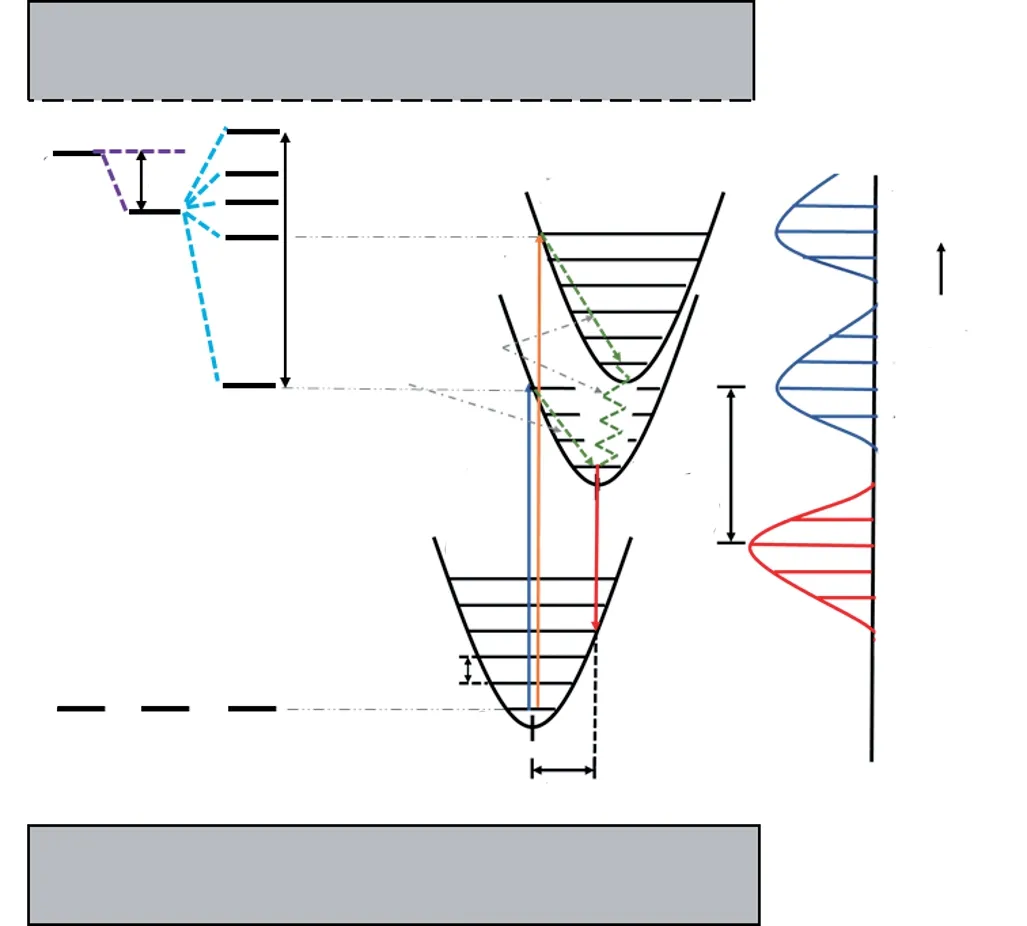
图5 Ce3+/Eu2+质心移动、晶体场劈裂和斯托克斯位移示意图，图中注明位形坐标模型中的振动能级和声子能量[7］。Fig.5 Energy level diagram showing the crystal field splittingεcfs，centroid shiftεc and the Stokes shiftΔS.The vibrational states and phonon energy are indicated in the configurational coordinate diagram[7］.

为进一步探索Ce3+/Eu2+掺杂无机发光材料的斯托克斯位移和基质材料组成以及结构之间的相关关系，我们课题组收集整理了60多种Ce3+/Eu2+掺杂无机发光材料的结构和光谱数据，系统研究了Ce3+/Eu2+取代的阳离子和配位阴离子特性对斯托克斯位移ΔS、声子能量ћω和黄昆因子S的影响[7]。化合物选取原则是：稀土离子占据单一晶体学位置，是单一发光中心，以便排除多发光中心由于光谱重叠对斯托克斯位移数据读取带来的误差。结果表明Ce3+/Eu2+取代的阳离子和配位阴离子特性对斯托克斯位移ΔS、声子能量ћω和黄昆因子S有重要影响。斯托克斯位移和有效平均配位键长Rav正相关。在卤化物和硫属化合物中，斯托克斯位移分别按照从氟化物到氯化物到溴化物和从氧化物到硫化物到硒化物的顺序依次降低；然而，在具有同一周期阴离子的化合物中，斯托克斯位移和阴离子类型没有明显的相关关系。在大多数情况下，声子能量和平均配位键长R负相关，而黄昆因子和平均配位键长正相关。此外，结果表明斯托克斯位移和阳离子配位数没有明显的相关关系。

在具有相同结构和阴离子类型的化合物中，黄昆因子S和平均配位键长R正相关，而声子能量ħω和平均配位键长R负相关。根据公式（14），黄昆因子S和晶格弛豫ΔQe正相关，晶格弛豫ΔQe即为电子被激发到激发态时电子云分布的改变使核的平衡位置发生的变化。因此，晶格弛豫ΔQe和化合物中阴离子与中心阳离子之间的配位键长密切相关。在镧系离子取代中心阳离子时，镧系离子在具有较长配位键长的基质材料中有较大的容纳空间，使电子在从基态跃迁到激发态时具有更宽松的空间调整其平衡位置，导致材料具有较大的晶格弛豫ΔQe。因此黄昆因子S和晶格弛豫ΔQe与平均配位键长正相关。由于斯托克斯位移和平均配位键长具有同样的正相关关系，因此，黄昆因子在斯托克斯位移和平均配位键长的正相关关系中起主导作用。

在具有相同结构和阳离子的化合物中，声子能量ћω在卤化物和硫属化合物中分别按照从氟化物到氯化物到溴化物和从氧化物到硫化物到硒化物的顺序依次减小，和斯托克斯位移与阴离子类型之间的相关关系一致。这一现象可以使用位形坐标模型进行理解。在晶格弛豫ΔQe相同的情况下，较大的振动频率使势能曲线的曲率较大，从而导致较大的斯托克斯位移。另一方面，原子质量在卤化物和硫属化合物中分别按照从氟到氯到溴和从氧到硫到硒的顺序依次增加，使得原子半径增加，电负性降低，从而导致中心阳离子和配位阴离子之间的化学键具有较软的属性。较大的阴离子质量和较软的化学键属性使基质材料晶格的振动频率较小，导致其较小的声子能量。

在具有同一周期阴离子的化合物（例如氟化物、氧化物和氮化物）中，斯托克斯位移不随阴离子种类的改变而改变。如上所述，斯托克斯位移主要取决于镧系离子占据空间位置的大小和结合键的强度。前者较易理解，因为同一周期元素具有相似的原子半径。然而同一周期中阴离子配体的电荷对斯托克斯位移几乎没有影响，可以通过有效电荷的概念对其进行理解，即使用阴离子的有效电荷Z=Q/N（Q（Ce3+）=3，Q（Eu2+）=2）代替形式电荷Z（卤化物为1，硫化物和氧化物为2，氮化物为3）[53]。

斯托克斯位移和阳离子的配位数没有明显的相关关系。这与晶体场劈裂不同，由于阴离子配体几何构型的影响，晶体场劈裂和阳离子配位数有明显的相关关系。斯托克斯位移主要取决于晶格弛豫ΔQe和势能曲线的曲率。一般情况下，较多的配位阴离子使发光中心在基质材料中占据较大的空间位置，因此电子在从基态跃迁到激发态时具有更宽松的空间调整其平衡位置，导致材料中晶格弛豫ΔQe较大。同时，空间越宽松，位形坐标模型中势能曲线的曲率越小。晶格弛豫ΔQe和势能曲线的曲率共同作用、相互抵消，使斯托克斯位移和阳离子配位数没有明显的相关关系[7]。

需要注意的是，用位形坐标模型去描述电声子耦合有一个假设：即仅考虑一种晶格振动模式，呼吸振动模式。显然，该模型做了简化处理，在用来理解斯托克斯位移与组分和结构的关系时，可能得不到满意的解释。另外，当发光中心离子进入晶格后，由于晶格弛豫，会引起局域结构的复杂变化。因此，需要考虑局域结构的变化对斯托克斯位移的影响，从而解释对发射光谱移动的影响规律[8,43,54]。另外，通常随着激活离子浓度的增加，发射光谱由于晶体场的变化和重吸收效应发生红移，斯托克斯位移变大[55]。

2.5 发光效率、发光热猝灭、缺陷和长余辉发光

发光材料的内量子效率定义为发射光子数和吸收光子数之比[56]。当电子从基态激发到激发态后，可以通过两种途径返回基态，分别为辐射跃迁和非辐射跃迁。辐射跃迁即指发光，非辐射跃迁则指能量以除发光以外的形式耗散掉，通常又称为发光猝灭[57]。因此，辐射跃迁速率和非辐射跃迁速率二者之间的比值决定了荧光粉的发光效率。通常非辐射跃迁有多种通道，源于不同的物理机制。

目前，学者们普遍认可的Ce3+/Eu2+掺杂无机发光材料的发光猝灭机制或非辐射跃迁过程主要有三种：基于位形坐标模型的基态和激发态的交叉弛豫、基于材料电子结构的5d电子到导带的离化、以及杂质和缺陷导致的发光猝灭[58-61]。对于位形坐标模型，足够的热能可以帮助激发态电子达到较高的振动能级。如果这一振动能级到达或高于基态和激发态势能曲线的交点，激发态电子则借助声子（晶格振动）释放能量通过交点回到基态，导致发光猝灭[15,61]。由于势能曲线的交点位置取决于材料的声子能量ћω和黄昆因子S，所以在位形坐标模型中，荧光粉的室温发光效率和热猝灭特性主要由材料的声子能量ћω和黄昆因子S决定。研究发现刚性结构有助于抑制发光猝灭从而实现较高的发光效率，并提出使用德拜温度判定材料的结构刚性[62]。在电子离化模型中，5d1激发态电子可以被光电离或热电离至导带。随后，离化电子非定域化并在整个晶体中移动，这增大了其被缺陷陷阱捕获的概率，从而导致发光猝灭[59,63]。在电子离化模型中，发光效率和发光热猝灭特性主要取决于5d电子的离化能，即5d电子能级和基质化合物导带底的能量差。在杂质和缺陷导致发光猝灭模型中，激发态能量可以传递到缺陷（包括表面缺陷）或杂质能级，从而导致发光猝灭。这种传递的发生仅限于杂质或缺陷与激活剂离子足够接近的情况，或激活剂离子的浓度足够高。随着激活剂离子浓度增加和随温度升高，激活剂离子之间能量传递增强，辐射跃迁概率减小，非辐射跃迁概率增加（例如，能量传递到杂质或缺陷能级的概率增强），从而导致发光猝灭，这一过程与浓度猝灭密切相关[61]。值得注意的是与这些杂质和缺陷相关的猝灭过程不是材料固有的，可以通过优化合成条件减少缺陷和杂质浓度以及改变发光中心浓度等方法来提高材料的发光效率和抗热猝灭特性。与位形坐标模型和电子离化模型相关的发光热猝灭是材料的固有特性；与4f和5d势能曲线的交点以及激活剂离子5d能级相对于基质导带底的相对能量位置相关。人们可以通过合适的基质化合物、或对已有荧光粉进行改性，来调控电声子耦合和电子结构，从而提高其发光效率和抗热猝灭性能[58-61,64-65]。

基于位形坐标模型的基态和激发态的交叉弛豫过程中，激发态电子直接回到基态，导致发光热猝灭。基于材料电子结构的5d电子到导带的离化过程，激发态电子没有回到基态，而是被激发到导带中或被电子陷阱捕获；随着温度升高，这部分电子被热激发通过导带回到5d态，再跃迁到4f基态发光。这通常导致在测量过程中，发光强度随温度升高而增强，使得材料表现为发光零热猝灭或热猝灭反常[9]。另一方面，这部分被陷阱捕获的电子如果在室温下被热激活就会导致长余辉发光，在光激励下被激活就会导致光激励发光。

在高性能荧光粉基础上，基于电子结构，通过调控带隙、5d能级与导带底的能量差、缺陷类型、缺陷深度和浓度，可实现长余辉发光和光激励发光。例 如，在Y3Al5O12∶Ce3+中，通 过Ga替 代Al调控带隙，掺杂Yb3+、Cr3+、B3+等引入合适的陷阱，获得了优异的黄绿超长余辉发光材料[66-69]。在（Ba,Sr）3SiO5∶Eu2+中通过掺杂Ge调控带隙，引入Nb5+获得合适的陷阱，制备出了可被太阳光激发的暖色调超长余辉发光材料（图6（a）～（d））[70-72]。对于（Ca,Sr）AlSiN3∶Eu2+、β-Sialon∶Eu2+和SrLiAl3N4∶Eu2+，最低5d与导带底的能级差较大；可利用短波长的激发光，把Eu2+的基态4f电子直接激发到导带，随后被陷阱捕获，实现长余辉发光或光激励发光。这些材料的余辉激励过程与SrAl2O4∶Eu2+,Dy3+长余辉发光的激励过程明显不同（图6（e）～（f））[73-75]。

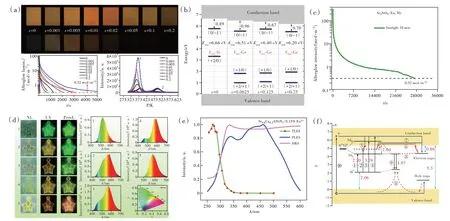
图6 （a）Sr3（Si1-xGex）O5∶Eu2+（x=0～0.2）的余辉性能[70］；（b）Sr3（Si1-xGex）O5（x=0，0.062 5，0.125，0.25）中氧空位的热力学电荷转移能级示意图[70］；（c）Sr3SiO5∶Eu2+，Nb在阳光下照射10 min后的余辉衰减曲线[71］；（d）SrAl2O4∶Eu2+，Dy3+和Sr3SiO5∶Eu2+，Nb封装器件余辉性能示意图[71］；Sr0.8Ca0.2AlSiN3∶Eu2+的余辉激发光谱（e）和余辉机制（f）[73］。Fig.6（a）The persistent luminescence properties of Sr3（Si1-xGex）O5∶Eu2+（x=0-0.2）[70］.（b）Calculated thermodynamic charge transition levels for the most stable oxygen vacancies in Sr3（Si1-xGex）O5（x=0，0.062 5，0.125，0.25）[70］.（c）Persistent luminescence decay curve of Sr3SiO5∶Eu2+，Nb after sunlight irradiation for 10 min[71］.（d）Persistent luminescence property of devices fabricated with SrAl2O4∶Eu2+，Dy3+and Sr3SiO5∶Eu2+，Nb[71］.（e）PLE，TLE and DR spectra of Sr0.8Ca0.2AlSiN3∶0.15% Eu2+[73］.（f）Persistent luminescence mechanism for Sr0.8Ca0.2AlSiN3∶xEu2+[73］.

发光材料的热稳定性、长余辉发光和光激励发光与材料的电子结构密切相关。因此，深入理解稀土掺杂无机化合物的电子结构对设计研发高效发光材料、长余辉发光材料和光激励发光材料等具有重要意义。

2.6 稀土掺杂无机化合物的电子结构

稀土掺杂发光材料的发光性能，包括激发和发射谱的位置、发光热稳定性、闪烁性能以及长余辉性能等，主要取决于稀土离子相对于基质材料导带底和价带顶的电子能级结构[76]。2003年，Dorenbos在Dieke图的基础上，结合光谱数据和稀土离子电子结构信息构筑电子结构图，给出了二价、三价稀土离子的4f、5d各能级相对于基质化合物导带底和价带顶的能量位置以及它们相对于真空的能量位置，称为HRBE图（Host referred binding energy）和VRBE图（Vacuum referred binding energy）[77-79]。

图7为LaF3的HRBE图 和VRBE图[26]。图 中双“之”字形曲线①和③分别连接二价稀土离子Ln2+和三价稀土离子Ln3+的4f基态电子能量，曲线②和④分别连接Ln2+和Ln3+的最低5d激发态电子的能量。大量的理论和实验证明，在所有的无机化合物中，HRBE图中四条曲线的形状几乎不变[80]。基于自由二价和三价稀土离子的电离能数据，使用化学位移模型、镧系收缩模型以及大量的实验数据进行修正，2017年，Dorenbos给出电子结构图曲线形状参数[80]。因此，电子结构图的构筑主要基于化合物依赖的3个参数：（1）基质化合物导带底和价带顶之间的能量差，即带隙能量Eg（箭头a）；（2）Ln2+的4f基态相对于基质价带顶的能级位置（箭头b）；（3）Eu2+和Eu3+基态4f电子能量的能量差U（6，A）（箭头c）[53]。基质化合物的带隙Eg可以由激子能量Eex得到，根据经验公式

图7 LaF3的HRBE图和VRBE图[26］Fig.7 HRBE and VRBE diagrams of LaF3[26］

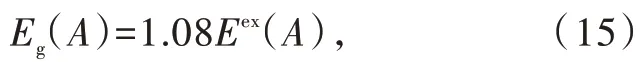
其中激子能量Eex可以通过紫外漫反射或真空紫外激发光谱得到[26]。Ln2+的4f基态相对于基质带隙的能级位置，目前主要有三种获得途径。一是通过激发使电子直接从价带进入Ln3+的4f壳层，使Ln3+变 为Ln2+，即 电 荷 迁 移（Charge transfer）。Ln3+的电荷迁移带（Charge transfer band）峰位对应的能量即为价带顶和Ln2+的4f基态能级之间的能量差[77]。第二个方法为通过光子激发Ln2+，使电子从4f基态直接进入导带，并检测光电流强度。相应峰位对应的能量即为Ln2+的4f基态能级和导带底的能量差[81]。最近，我们课题组提出了第三种方法，即利用某些化合物的余辉激发光谱的起始能量作为4f基态与导带底的能量差以确定Eu2+（或Ce3+）的4f能级位置[73-74]。Eu2+和Eu3+基态4f电子能量的能量差称为U（6，A），即4f电子间库伦排斥能[82]。由 于U（6，A）与Ce3+5d能级质心移动εc（1,3+,A）都取决于晶格中稀土离子周围的配位环境，2013年Dorenbos在大量实验数据的基础上提出使用εc（1,3+,A）计算U（6，A）的经验公式[26,83]

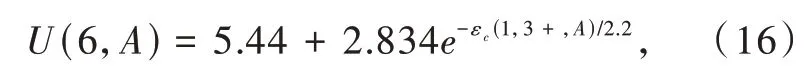
当Ln2+和Ln3+的4f基态能级位置确定后，通过光谱数据，可以较容易地得到其最低5d激发态电子的能级位置，完整地绘制出HRBE图。随后，Dorenbos建立了化学位移模型[53]。基于Eu2+的4f电子和周围化学环境的交互作用，假设周围电荷平均分布，得到化学位移值E4f（7,2+,A），即在化合物A中Eu2+的4f电子电离能，与U（6，A）的关系公式[53,84]

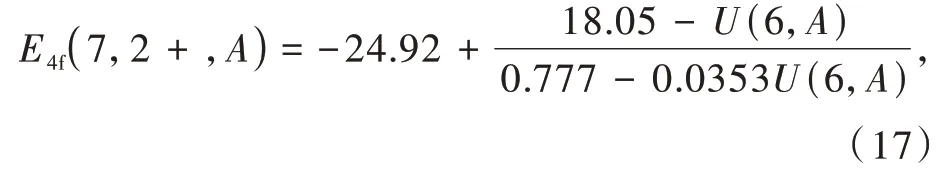
由于各镧系离子之间4f以及5d能级的相对能量在化合物中保持不变，所以根据化合物中Eu2+4f电子电离能可以得到该化合物中所有二价和三价镧系离子的4f以及5d电子的电离能，完整地绘制出VRBE图。

HRBE图和VRBE图提供14种二价、三价稀土离子的4f、5d能级和基质化合物电子结构的能量信息。电子结构图不仅可以预测14种稀土离子的能级结构、材料带隙结构和稀土离子价态，而且可以帮助我们通过调节镧系离子基态、激发态能级和基质晶格价带、导带的相对位置，改善稀土掺杂无机发光材料的发光性能[85]。

提供各稀土离子能级结构。在化合物中，只要得到任何一种稀土离子的能级结构信息，根据曲线形状参数，可以直接预测其他13种稀土离子在该化合物中的能级结构。

给出基质化合物价带顶和导带底的能量位置。VRBE提供稀土离子4f和5d能级，以及基质价带顶和导带底相对于真空（0 eV）的能量信息，这使得所有基质化合物处在价带顶和导带底的电子能量具有可比性。我们可以得到不同化合物价带顶和导带底电子能量随其化学组成和结构的变化规律，从而用于分析和预测化合物的电子结构和性能，同时帮助设计满足应用需求的新型发光材料。

预测稀土离子的稳定价态。Dorenbos假定费米能（Ef）位于导带底和价带顶的中间位置。进一步假设少量稀土掺杂几乎不影响化合物的费米能，则低于费米能的能级应被占据，而高于费米能的能级应被闲置，即稀土离子价态取决于Ln2+4f基态电子电离能和费米能级的能量差（EFf=E4f（Ln2+）-Ef）。若化合物中EFf＜0,则稀土离子倾向于以二价态存在；若EFf＞0,则稀土离子倾向于以三价态存在[86]。

解释发光热猝灭特性。发光热稳定性和Ce3+/Eu2+激发态5d电子到导带底的能量差密切相关。5d电子到导带底的能量差越小，越容易离化到导带，发光热稳定性越差。电子能级结构图可以提供5d电子和导带底的相对能量位置，因而可以帮助我们理解分析以及设计调控材料的发光热稳定性。例 如，SrMg2Al2N4和SrMg3SiN4与SrLiAl3N4三个化合物晶体结构尽管空间群不同，但结构骨架非常相似，即具有Vierer环状骨架结构。我们基于光谱数据，构筑了这三个化合物的HRBE及VRBE图，阐明该系列荧光粉的发光热焠灭特性与机制[8]。

调控闪烁材料的性能。无机闪烁材料广泛应用于电离辐射探测领域。为了最大程度消除能量累积造成的重影，闪烁材料要求具有较快的衰减时间。材料中缺陷的存在会延长其衰减时间，因此，我们可以利用电子能级结构图，调节材料带隙和缺陷能级之间的相对能量，设计调控闪烁材料的性能[87]。

设计和调控长余辉发光材料的性能。HRBE图和VRBE图不仅为分析材料的长余辉机理提供依据，同时提供两种调控长余辉发光材料的长余辉性能的途径，分别称为能带工程和缺陷工程。能带工程即通过阴/阳离子取代的方式，改变基质材料的带隙，从而改善其长余辉性能。缺陷工程即通过选择合适的稀土掺杂离子，调控陷阱能级与基质带隙能级结构的相对位置，调节长余辉发光材料的长余辉性能[68,88]。

3 局域结构与发光性能调控

由于5d轨道受配位环境的影响大，因此局域结构对Ce3+/Eu2+掺杂无机发光材料的性能有重要影响。前文也表明局域结构与晶体场劈裂、诱导效应、斯托克斯位移、发光效率和发光热猝灭等密切相关。

X射线衍射分析（XRD）是测定无机材料晶体结构最重要的技术手段，但其主要表征的是具有周期性的平均结构，对局域结构的分析还需要结合其他方法，如透射电镜[89]、晶体学和固体化学的知识[90-91]。另外，由于固体中稀土或过渡族金属离子的发光对局域结构的变化非常敏感，因此可通过光谱分析来推测局域结构[24,54]。例如，对于Ce掺杂的SrYSi4N7荧光材料中Ce3+的晶体学位置，存在两种看法：一是Ce3+被认为占据碱土金属离子Sr2+的位置，二是被认为占据Y3+位置。两种看法都有一定的依据，而且由于Ce3+离子的掺杂量通常较小，很难通过常规手段比如XRD测定具体占位。但是，借助光谱与成分和结构的关系式，通过Ce3+掺杂的SrYSi4N7的光谱性能，来推测Ce3+离子的真实占位。结果表明Ce3+离子在SrYSi4N7中，占据的是Sr2+位置[24]。

荧光粉通常是粉末材料，而粉末衍射数据由于颗粒择优取向等因素，会导致衍射强度出现偏差，从而影响基于Rietveld结构精修方法解析原子占位和占有率的准确性。因此，用XRD来测定掺杂浓度较低的原子占位具有较大不确定性。另外，XRD很难分辨原子序数相近的原子或离子。但是，XRD对于晶格常数的测量和分析通常具有很小的误差，因此有时可利用晶格常数的变化来分析晶体结构。例如，对于Sr2-2xEu2xSi5N8荧光粉，尽管Sr2+离子半径（0.121 nm，7配位）与Eu2+离子半径（0.120 nm，7配位）相差非常小，但即使用很少量的Eu2+替代Sr2+，也会在实验上测量到晶格常数的减小[55]。例如，我们基于晶格常数随成分的变化并结合结构化学知识确定了氧原子在CaAl-SiN3∶Eu2+结构中的占位[90]。

分析局域结构通常需要晶体学和固体化学的知识。晶体学将晶体中具有周期性规则排列的原子位置抽象为格位（Site）。每一种空间群都包含若干种格位，这些格位的对称性（Site symmetry）各不相同，一般用Wycokff符号加以区分。该符号由数字和字母构成，其中数字表示多重度（Multiplicity），即一个单胞中该格位的等效数目；字母用来表示对称性的高低。例如，对于Y3Al5O12,按照晶体学位置可表述为{A}3[B]2（C）3O12，{A}代表8配位十二面体的24c格位，[B]为6配位八面体的16a格位，（C）为4配 位 四面体 的24d格 位[33]。Ga替代Al时优先占据24d格位，也可占据16格位。由于存在反位缺陷，部分Y可以占据[B]位，部分Al则可占据{A}位置。格位是由对称性而非化学元素所决定的；同一种原子可以占据不同的格位，而不同的格位可以容纳相同的原子。因此，用元素符号表示格位容易引起混淆，可用其他符号表示。例如，在（Sr,Ba）SiO4∶Eu2+中有两种4c格位，其原子坐标不同，且配位数分别为10和9。Sr和Ba在这两种格位上虽存在择优占位，但在两个格位上均有分布；因此如果用“Sr位”或“Ba位”容易引起混淆。此时可单独定义对应于10配位、9配位的M格位、M’格位来描述具体的占位情况[15]。在T相（Ba,Ca）2SiO4∶Eu2+的晶体结构中，5个晶体学位置（Wyckoff site）发生了原子格位劈裂。这需要利用晶体学分析其局域结构。分析发现产生原子格位劈裂的原因是为了优化成键；这使该相结构刚性增强，从而导致了发光热猝灭性能的提升[91]（图8）。

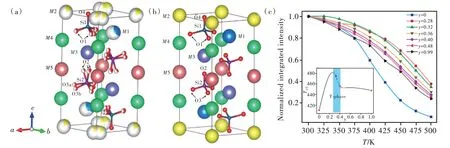
图8 T-相（Ba，Ca）2SiO4的晶体结构：（a）原子格位劈裂模型，（b）原子格位不劈裂模型，（c）发光热猝灭特性[91］。Fig.8 Crystal structure of T-phase（Ba，Ca）2SiO4：（a）atom-split model，（b）atom-unsplit model，（c）thermal luminescent quenching characteristics[91］.

容忍因子（Tolerance factor）最早由Goldschmidt从钙钛矿结构中提出，它可以表征某一结构类型的晶体化学特征[92]。我们课题组通过结构分析和统计方法，构筑了石榴石、尖晶石和烧绿石系列化合物的结构容忍因子（图9），为建立从成分出发计算预测结构和相稳定性的理论模型提供了重要的依据[33,93-94]。利用容忍因子快速判别具有特定化学组成化合物的相稳定性，避免了第一原理计算所需要的大量计算。另外，利用烧绿石型结构容忍因子还可以从成分出发计算预测烧绿石型化合物的原子有序-无序的占位[94]。结构容忍因子可为基于材料基因工程的理念和技术去计算和筛选化合物提供重要依据。

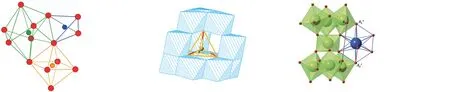
图9 石榴石、尖晶石和烧绿石结构的容忍因子表达式[33，93-94］。Fig.9 Tolerance factors of garnet，spinel and pyrochlore structures[33，93-94］.

作为发光中心的稀土或过渡族金属离子替代占据晶体中的某一格位后，由于与基质晶格中其他相同格位的化学元素不同，会导致晶格弛豫。替代后的配位多面体尺寸和形状与原基质相比有所改变或调整。在晶体材料中，配位多面体相互之间通过共顶点、共棱或共面连接[33]。掺杂离子所处的配位多面体的调整受到周围多面体的影响和制约，从而使局域结构分析变得困难和复杂。例如，在Cr3+掺杂的KMP2O7中，基质八面体格位M分别为Ga、Sc、In、Lu时，观测到KMP2O7∶Cr3+材料源于Cr3+的发射峰的峰位和强度随M的变化明显不同，表明该结构中Cr3+替代后晶格弛豫较小[95]。然而，对于Sr9M（PO4）7∶Cr3+（M=Ga,Sc,In,Lu）荧光粉，所有样品在485 nm光激发下在850 nm附近呈现一个宽带近红外发射峰位，发射峰位几乎不随M元素类型发生变化，表明该结构中Cr3+替代后晶格驰豫很大[96]：由于结构限域效应，尽管基质中M元素的离子半径不同，但替代后Cr3+的配位多面体体积和形状几乎相同，因而发射峰位相同。

总之，局域结构对Ce3+/Eu2+掺杂无机发光材料的发光性能影响很大。局域结构的变化和分析具有复杂性。因此，需要综合考虑发光理论、晶体学，并结合先进的结构和光谱分析技术，来理解发光材料的构效关系。下面我们以YAG∶Ce3+和CaAlSiN3∶Eu2+为例，说明局域结构与发光性能的关系。

3.1 铈掺杂石榴石型发光材料

Ce3+掺杂石榴石结构荧光粉中的“反石榴石效应”是局域结构调控发光性能的一个典型例子。在（A24c）3{B16a}2[C24d]3O12中的三个阳离子格位分别替换较大半径的离子，例如A位Gd替换Y∶（Gd）3{Al}2[Al]3O12→（Y）3{Al}2[Al]3O12,B、C位Ga替换Al∶（Y）3{Ga}2[Ga]3O12→（Y）3{Al}2[Al]3O12，都会导致晶格常数变大、多面体体积膨胀、平均键长增加等趋势一致的平均结构变化规律。然而，前一种情况下晶体场劈裂变大，后一种情况下晶体场劈裂变小[31]。这一自相矛盾的现象无法用平均键长的5次方反比关系来解释。实际上，对于互相连接的多面体，其中一个多面体的改变会造成邻近多面体的协同变化，而正是这种协同变化造成了平均结构一致变化趋势之下局域结构的差异。对于YAG中容纳发光离子Ce3+的十二面体，Gd→Y和Ga→Al两种替代方式会导致不同的配位迁移模式，如图10（a）所示，并使十二面体产生沿不同方向的四方变形（Tetragonal distortion）[34]。晶体场分析表明，四方变形主导了Ce3+在石榴石结构中的晶体场劈裂[31,97-98]。我们通过多面体建模及晶体场定量计算的方式，研究上述十二面体的形变方式对于能级劈裂的影响。利用群论推导三价铈离子在D4h和D2对称性下的5d能级分布情况，发现最低和次低能级不再发生劈裂[99]。结果表明，石榴石晶体结构与三价铈离子晶体场劈裂之间不再是简单的五次方反比关系，而是与所占据的十二面体扭曲形变有关。石榴石结构中的三种阳离子多面体位的扭曲存在一种竞争关系，从而导致非均匀形变。对于Ce3+占据的多面体，虽然从平均结构上看多面体尺寸在增加，但相邻多面体的协同变化导致了局域结构的不同，从而使晶体场劈裂表现出复杂的“反石榴石效应”。这也同时说明，用来判断晶体场劈裂大小的5次方反比关系有局限性，不能以平均键长为唯一判断依据，还应考虑配位彼此间的相对位置。

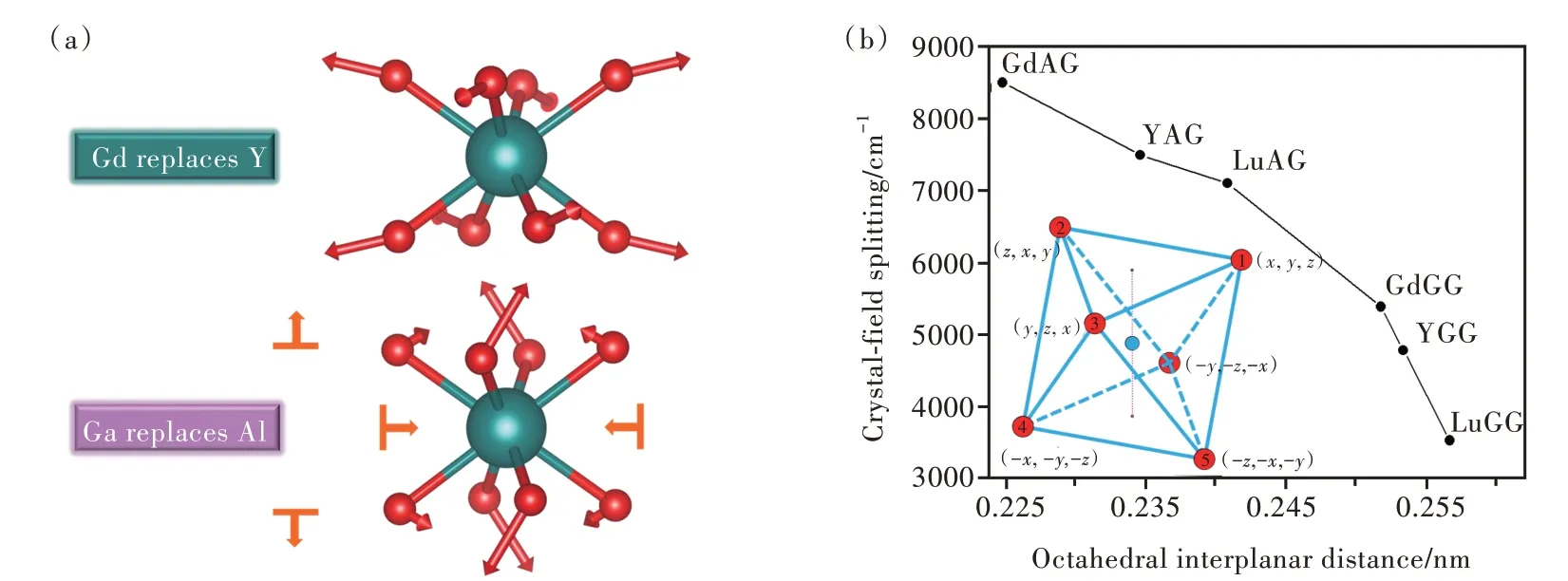
图10 （a）YAG中不同格位替代导致的配位迁移模式[34］；（b）不同石榴石型化合物中晶体场劈裂与八面体面间距的对应关系[35］。Fig.10（a）Different ligand moving patterns caused by multiple site substitutions in YAG[34］.（b）Crystal-field splitting as a function of octahedral interplanar distance for different garnet series[35］.

我们课题组进一步尝试从石榴石的结构特点出发，找到了能够表征Ce3+晶体场劈裂的指示符[35]。不同石榴石荧光粉中晶体场劈裂与结构指示符的关系如图10（b）所示，可见该指示符能够较好地反映石榴中不同格位元素替代导致的晶体场劈裂变化，从而可以根据成分和结构预测相应材料的发光性能[35]。在YAG中，用氮替换氧能够实现Ce3+发光的红移。理论计算和晶体结构测定表明，氮元素替代后会扩张十二面体，造成Ce3+的晶体场劈裂增加，进而造成光谱红移[36]。

3.2 局域结构对CaAlSiN3∶Eu2+系列固溶体发光性能的影响

CaAlSiN3∶Eu2+荧光粉在蓝紫光区有宽的吸收带，且发射红光[54，90］。该荧光粉具有良好的化学稳定性和温度猝灭特性，以及高量子效率，在白光LED中已得到应用。但是该荧光粉的发射主峰偏红，大约在650 nm，致使采用其封装的白光LED的光效偏低。为了进一步改善CaAlSiN3∶Eu氮化物荧光材料的发光特性，在CaAlSiN3∶Eu中掺入O调控其波长，使其蓝移至与白光LED最匹配的620 nm。CaAlSiN3具有正交晶系结构，空间群为Cmc21，其 中Ca占 据4a位 置，Al和Si无 序 占 据8b位置，N原子占据两种晶体学位置：8b和4a，分别标记为NI和NⅡ，单胞中NⅠ的数目是NⅡ的2倍。因此，CaAlSiN3的晶体化学式可以表示为Ca（Al-Si）2NI

2NⅡ。随着O含量的增加，晶格常数a和晶格常数比a/b逐渐减小，而晶格常数b几乎保持不变。根据晶格常数沿不同方向的变化规律不同，我们推定O原子在CaAlSiN3∶Eu结构中择优替代NⅡ原子[90]。最终，我们将含O的CaAlSiN3的晶体化学式表达为Ca（Al/Si）2NI（2NⅡ1-xOx）。为了进一步调控A位和B位阳离子，我们课题组设计和制备 出 了（Ca1-xLix）0.98（Al1-xSi1+x）N3∶0.02Eu2+连 续 固溶体。通过XRD衍射图谱及其晶格常数随成分的变化图可看出，样品皆为纯相。随着x的增大，样品的衍射峰向高角度方向移动，晶格常数相应线性变小，符合Vegard定律。从图11（a）可以看出，激发光谱的高能端几乎保持不动，而低能端随着x增大而发生蓝移。这意味着激发光谱的重心位置发生了蓝移，光谱的半高宽（FWHM）变窄，即5 d能级的劈裂变小。在固溶体（C a 1-x L i x）（A l 1-x S i 1+x）N 3的晶体结构中，随着x增大，晶格常数变小，单胞体积也相应变小。在这种情况下，E u 2+离子的5 d能级劈裂应逐渐增大，发射光谱红移并逐渐加宽，这与观察到的现象正好相反。我们认为这种异常现象有两方面原因：一是E u 2+离子与配位的阴离子之间的距离没有变小，反而为了容纳更小的L i+离子，临近的E u 2+所处的配位多面体变大；二是由于S i 4+替代A l 3+后化合物平均电负性发生改变，引起光谱极化率减小。该固溶体的发射光谱呈现了三个阶段的变化过程，如图1 1（b）～（d）所示。第一阶段：随L i/S i量的增加，发射光谱有微小蓝移，从6 6 9 n m到6 6 3 n m；第二阶段，从6 6 3 n m到7 3 8 n m的大幅度红移；第三阶段，当x=1时，发射光谱突然大幅度蓝移至6 0 0 n m。通过对晶体结构和发光中心局域结构的分析，提出了如图1 1（g）所示的模型来解释化学成分连续变化时发射光谱不连续变化的现象。

图11 （Ca1-xLix）0.98（Al1-xSi1+x）N3∶0.02Eu2+（x=0～1）的发射光谱（a），及不同Li-Si替代量的激发光谱：（b）x=0～0.2，（c）x=0.3～0.9，（d）x=0.8～1；（e）光谱参数λc、λabs、λem和λ0随x的变化规律；（f）斯托克斯位移随x的变化规律；（g）（Ca1-xLix）0.98（Al1-xSi1+x）N3∶0.02Eu2+固溶体从CaAlSiN3（x=0）端元到LiSi2N3（x=1）端元的结构演化模型[54］。Fig.11（a）The excitation spectra of（Ca1-xLix）0.98（Al1-xSi1+x）N3∶0.02Eu2+（x=0-1）samples with x=0-1，and the emission spectra of（Ca1-xLix）0.98（Al1-xSi1+x）N3∶0.02Eu2+samples for different ranges：（b）x=0-0.2，（c）x=0.3-0.9，（d）x=0.8-1.（e）The wavelength ofλc，λabs，λem andλ0 as a function of x.（f）The Stokes shift as a function of x.（g）The proposed model on the chemical unit co-substitution strategy represented by structural evolution of（Ca1-xLix）0.98（Al1-xSi1+x）N3∶0.02Eu2+：from CaAlSiN3（x=0）to LiSi2N3（x=1）via the（LiSi）5+substitution for（CaAl）5+couple[54］.

在 固 溶 体（Ca1-xLix）0.98（Al1-xSi1+x）N3∶0.02Eu2+的晶体结构中，发光离子周围由呈六圆环形状排列的[AlN4]和[SiN4]四面体相间排列而成，有且只具有四种组合情况：3个[AlN4]和3个[SiN4]四面体（记为M1），2个[AlN4]和4个[SiN4]四面体（记为M2），1个[AlN4]和5个[SiN4]四面体（记为M3），以及全部6个[SiN4]四面体（记为M4），四种情况如图11（g）所示。从M1到M4，发光中心离子的配位环境发生了从均匀到不均匀、再到均匀的变化情况。采用该模型能够很好地解释固溶体（Ca1-xLix）0.98（Al1-xSi1+x）N3∶0.02Eu2+的 发 光 特 性 随成分的变化规律。

4 前景展望

Ce3+/Eu2+掺杂的无机发光材料由于其光谱可调、高内/外量子效率和高发光热稳定性受到人们的广泛关注，并具有广泛的应用，如在LED照明和液晶背光源领域，以及作为长余辉发光材料和闪烁材料等。近年来，面向类太阳光LED健康照明和超高色域液晶显示技术的发展，迫切需要研发新型高效深红-近红外发光材料[100-101]、紫光/蓝光激发的全光谱LED照明用荧光粉[102-103]，以及窄带发射的绿光和红光发光材料[4,104]。但是，目前在这一领域仍存在一些问题，特别是在理论方面，需要人们深入研究和解决。

4.1 斯托克斯位移与材料组分和结构的定量关系

建立发光材料组分和结构与斯托克斯的相关关系对于预测荧光粉发射性能至关重要。受到荧光粉光谱数据数量和质量的限制，目前仅得到了材料组分和结构与斯托克斯位移的定性相关关系。因此，随着Ce3+/Eu2+掺杂无机发光材料的实验数据的积累、理论发展和计算能力的增强，深入探索材料组分、晶体结构和局域结构与斯托克斯位移之间的内在关系和电声子耦合作用，将对新型高性能发光材料的研发提供科学依据。

4.2 发射带半峰宽与材料组分和结构的关系

窄带发射无机发光材料既可协同提升照明器件的显色指数和流明效率（如窄带红色发光材料）,也可增大液晶显示器件的色域（如窄带蓝色、绿色和红色发光材料），在照明和显示用发光二极管（Light-emitting diodes,LED）器件中具有重要的应用前景。因此研究发光材料组分和结构与半峰宽的相关关系将为研发新型窄带发射无机发光材料提供重要指导。

4.3 发光效率和热猝灭特性与组分和结构的关系

发光效率是评判荧光粉发光性能的重要参数，在荧光粉的实际应用中至关重要。研究发现刚性结构有助于抑制发光猝灭从而实现较高的发光效率，并提出使用德拜温度判定材料的结构刚性[62]。然而，发光效率和热猝灭特性与材料组分、晶体结构、局域结构和电子结构的定量关系尚不明确。因此探究影响发光效率的因素，揭示其与基质材料组分和结构的内在定量关系是今后研究的重要方向。

4.4 长余辉机理研究

目前，人们对长余辉发光材料的研究主要是通过实验的手段，比如，通过掺杂调控带隙或调控缺陷类型、缺陷的深度和浓度。通过第一性原理计算，也可分析材料的能带结构、本征缺陷能级和掺杂离子能级结构。但目前对长余辉发光机理仍存在很多争议。结合实验数据，理论上深入研究长余辉发光机理，对研发新型高性能长余辉发光材料具有重要意义。

5 结 论

我们总结了近年来Ce3+/Eu2+掺杂无机发光材料的唯象理论和构效关系研究进展，特别是基质材料组分和结构与Ce3+/Eu2+5d能级质心移动、晶体场劈裂以及斯托克斯位移的相关关系的研究进展。同时总结了诱导效应、局域结构和电子结构对发光性能的影响规律；并通过论述荧光猝灭机理，总结了影响发光效率、发光热猝灭特性和长余辉性能的因素。最后，对唯象理论和构效关系的未来发展提出了展望。

本文专家审稿意见及作者回复内容的下载地址：http://cjl.lightpublishing.cn/thesisDetails#10.37188/CJL.20220191.