一种面向立体跨域耦合任务的无人集群协同任务规划技术
2022-10-12梁月乾
梁月乾, 张 潇, 杨 毅
(1. 中国电子科技集团公司智能科技研究院, 北京 100041;2.海军装备部装备招标中心, 北京 100080)
0 引 言
近几年来,集群系统的巨大优势受到了越来越多的关注。特别是当集群是由搭载不同类型载荷的来自陆、海、空不同域多种不同类型平台组成时,每个集群成员可以充分发挥各自的优势,多个集群成员组成的子群可以优势互补,相比于由同类型平台组成的同构集群,这使得整个异构集群能高效完成更为复杂的体系任务。异构集群能充分显示其整体效能的一项基本保证是合适的任务规划。任务规划涉及在诸多实际约束条件下,如何安排每个集群成员或每个子群在每个任务阶段的角色,使某项整体效能达到最优。
任务规划方法大致可以分为两类[1]:精确优化方法和启发式方法。精确优化方法利用匈牙利法、分支定界法等对建模的旅行商问题、车辆路由问题、网络流问题等进行求解,通常可以得到最优任务规划方案[2-3]。启发式方法包括从生物系统的群集行为中发现的遗传算法、粒子群优化算法、蚁群优化算法等[4-8],以及从社会规律中发现的基于市场机制的方法等[9-10]。通过设置不同迭代次数,启发式方法可以获得不同优化程度的任务规划方案。
本文以异构集群的立体跨域协同为背景,研究存在不同类型和任务域的多个目标区域、处于不同任务域的多种集群平台的耦合时序任务的协同规划问题。
1 立体跨域耦合任务规划模型
1.1 问题描述
考虑一个由多个任务域的无人装备组成的跨域集群对多个陆域、海域选定目标区域执行类型1~4四种耦合任务的场景。这四种任务之间存在时序关系:类型1任务需要在其他任务开始前完成;类型4任务需要在类型3任务完成后执行;当需要对同一个目标区域既实施干扰任务也实施类型3任务时,这里假设这两种任务需要同时执行。
设有M个目标区域,其中包含未知数量和类型的目标。将区域位置记为qm,m=1,2,…,M。陆域、海域目标区域的集合分别记为Bg、Bw。与所在域无关,假设目标区域包括三种类型:第一种类型的目标区域只需执行类型1、类型2任务;第二种类型的目标区域需要执行类型1、类型3、类型4任务;第三种类型的目标区域需要执行所有四类任务。这三种类型的目标区域的个数分别记为M1、M2、M3。不失一般性,可将这三种类型目标区域的集合分别记为A1={1,2,…,M1}、A2={M1+1,M1+2,…,M1+M2}、A3={M1+M2+1,M1+M2+2,…,M}。
根据各目标区域的大小、其中目标的可能数量及类型、目标在区域中的分布情况等,量化每个目标区域的不同类型任务的能力需求,即类型1任务能力需求QR,m、类型2任务能力需求QEI,m、类型3任务能力需求QA,m、类型4任务能力需求QDA,m,其中m=1,2,…,M。需求量为0,表示无需对相应目标区域执行该类型的任务。对每个目标区域,将其对应的四类任务分别记为m、M+m、2M+m、3M+m。任务总个数记为N=4M。根据前述三种目标区域类型,即A1、A2、A3,将需要执行的任务集合记为W1,将不需要执行的任务集合记为W2={1,2,…,N}-W1。
设集群由K个无人装备组成,其中K1个为跨域或两栖装备,K2个为陆域装备,K3个为海域装备。将陆域、海域无人装备的集合分别记为Cg、Cw。根据每个无人装备上搭载的载荷的性能,可以将其四类任务能力分别量化为PR,m、PEI,m、PA,m、PDA,m。对小型无人装备,可能只有一种任务载荷,即只有一个任务能力非0,其余任务能力均为0.将每个无人装备的平均任务速度记为Vk,航时记为Tk,初始位置记为qV,k,其中k=1,2,…,K。
1.2 模型建立

上述任务规划问题可以建模为混合整数线性规划(Mixed Integer Linear Programming, MILP)模型。该模型的目标函数为
(1)

(2)
其中,每个无人装备的任务总时间满足
(3)
所有无人装备需要满足其最大航时约束,即
(4)
为避免每个无人装备循环执行某些任务,形成子回路,需要加入Miller-Tucker-Zemlin子回路消除约束[11]。由于每个任务需要多个集群成员同时执行才能完成,所以原子回路消除约束需要变更为如下形式
(5)
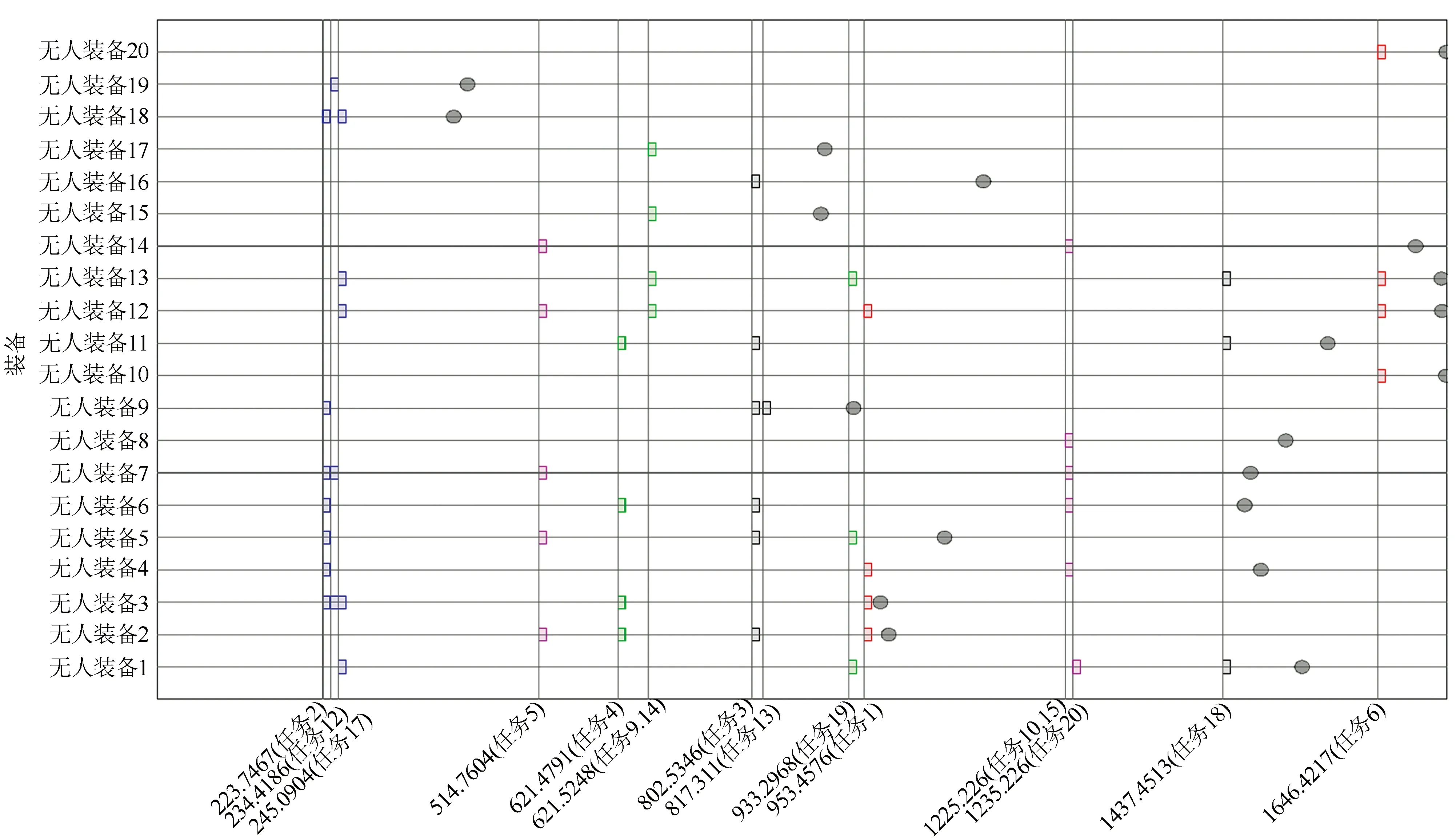
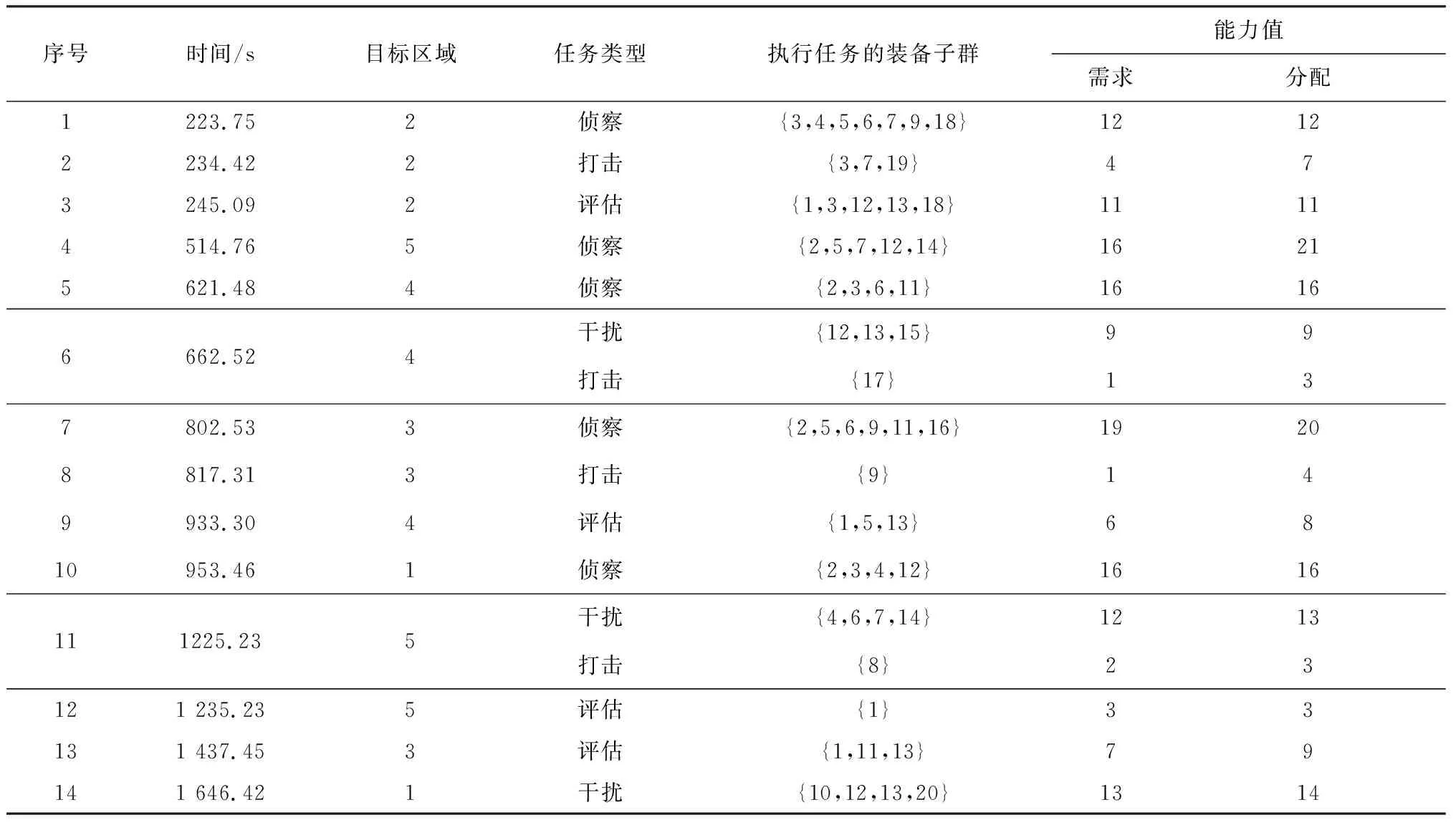
其中,整数决策变量满足ui 要保证完成每个需求任务,需要满足 (6) 其中,rj表示任务j的类型序号。 对每个无人装备,为保证其任务连续性,需要满足 (7) 即其到达哪个任务,下一步就需要从哪个任务出发。 对每个无人装备,它从初始状态出发,并最终回到初始位置,这要求 (8) (9) (10) 不同类型任务的时序关系要求下式满足 (11) 式中:Δt为对同一个目标区域的两个连续类型任务之间的最小时间间隔。 为节省任务时间,每个无人装备上的弹药全部用于对一个目标区域的攻击,而不是在多个目标区域各使用一部分弹药,这需要满足 (12) 不同域的无人装备只能执行其所在域的任务,据此,我们有 (13) 对无需执行的任务,有 (14) 对每个无人装备,当它的某种任务能力为0时,需要有 (15) 式中:i=0,1,2,…,N;j=(r-1)M+1,(r-1)M+2,…,rM;k=1,2,…,K;r=1,2,3,4且满足Pk,r=0。 分支定界法是求解混合整数线性规划问题的一种经典且有效的方法,该方法能保证得到问题的最优解(前提是问题有最优解)。该方法首先求解不考虑整数约束(称为松弛)的线性规划问题,根据其解对原问题进行“分支”,继续对分支问题进行松弛、求解,确定出原问题的上界和下界(“定界”),直到满足所有整数约束。 分支定界法的步骤为[12]: 步骤3:问题选取。从L中选取一个问题Pl,并将其从L中移除。 步骤5:添加割平面。寻找解xlR不满足的割平面。若能找到,将其添加到松弛问题,并转到步骤4。 考虑下面的立体跨域任务规划场景。集群由K=20个无人装备组成,其中13个(K1)为跨域装备,4个(K2)为陆域装备,3个(K3)为海域装备。各装备的航时、平均速度、任务能力值如1所示。共有5个目标区域,前两个为海面区域,后三个为陆地区域,即Bw={1,2}、Bg={3,4,5}。三种类型区域的集合分别为A1={1}、A2={2,3}、A3={4,5}。各区域的需求任务能力值如表2所示。 表1 各装备的航时、平均速度、任务能力值 表2 各区域的需求任务能力值 利用本文方法得到的任务规划结果如图1和表3所示。5个目标区域的任务分别用红色、蓝色、黑色、绿色、品红色方块表示,方块对应的横坐标为任务完成时间,对应的纵坐标为执行该任务的无人装备集。图中的椭圆形为每个无人装备的返回时间。从表4的第三、四列可以看到,不同类型任务的时序约束是满足的。表4的第六、七列分别为对应任务的能力需求值和分配给该任务的总能力值,可以看到,每个需求任务均由有足够能力的无人装备子群完成,第五列给出了完成每个需求任务的无人装备子群。不难看到,陆域无人装备(14、15、16、17)仅对陆域的目标区域(区域3、4、5)执行任务,而海域无人装备(18、19、20)仅对海域的目标区域(区域1、2)执行任务。若不计无人装备的返回,最优总任务时间约为1 646.42 s。若计入无人装备的返回,最优总任务时间约为1 718 s。 图1 任务规划结果 表3 任务规划结果 值得注意的是,除本文所使用的分支定界法外,一些常用的启发式方法,如蚁群算法、粒子群算法、遗传算法等,也可以用于求解所讨论的立体跨域耦合任务规划问题。本文所使用的分支定界法尽管所用计算时间较长,但能保证获取规划的最优解;相比之下,启发式方法虽然在问题规模较小、群体规模较小、迭代次数较少时计算时间较短,但并不能保证所获得的解为最优解,可能仅为局部最优解。因此,本文所述方法可以用于离线规划,启发式方法可以用于问题规模较小时的在线规划。 本文给出了一种基于分支定界法的面向立体跨域耦合任务的无人集群协同任务规划技术。任务规划以最小化总任务时间为优化目标,考虑了四种类型任务之间的时序约束关系,考虑了不同类型集群装备的任务域约束、载荷能力约束、航时约束等。从仿真结果中可以看到,所设计技术能为异构无人集群的跨域协同任务提供最优策略。作为一个未来的研究工作,我们将为立体跨域耦合任务规划问题寻求一种次优、计算代价较小的启发式解决方案。

2 分支定界法

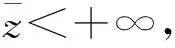

3 仿真结果


5 结 语
