基于Adam的电大目标快速仿真建模技术

郭良帅,李懋坤,许慎恒,杨 帆

（清华大学电子工程系,北京 100084）

0 引言

目标电磁散射与辐射特性在隐身与反隐身研究、雷达探测识别、天线优化设计、信道建模等领域具有重要意义。受限于目标电磁特性直接测量的高成本、长周期、高费效比等因素,电磁场仿真建模成为分析目标电磁特性的核心技术手段。

电磁场仿真建模方法主要有基于积分方程的矩量法（MoM）、基于微分方程的有限元法（FEM）及时域有限差分方法（FDTD）等。其中MoM自动满足辐射边界条件,更加适合求解电大目标电磁问题。基于MoM的快速仿真算法,如多层快速多极子（MLFMA）、区域分解（DMM）等,进一步提升了MoM的计算效率,可满足复杂中等电尺寸目标电磁场分析求解的需求。

采用MoM求解目标电磁场时,需求解矩阵方程以获取目标表面的感应电磁流系数,从而获取金属表面或介质体内的电磁流。矩阵方程的求解复杂度是决定计算效率的核心。LU分解法、高斯（Gauss）消元法等传统直接求解器的复杂度为O（N）（N为矩量法未知量数目）,仅能用于小维度矩阵方程求解。共轭梯度（CG）、最小残差余量（GMRES）等算法基于Krylov子空间的迭代求解器的计算复杂度为O（N）,较直接求解器具有更高的计算效率,但仍无法满足电大目标电磁场仿真建模需求。

降低MoM未知量数目的高阶基函数是一种降低计算复杂度的有效方法,通过增大离散网格密度,可以有效降低目标离散单元个数,减小阻抗矩阵方程维度,从而提升计算效率。但对于电大目标,该方法的矩阵方程计算复杂度仍无法满足要求。文献[7]将自适应矩估计（adaptive moment estimation,Adam）用于电小目标电磁仿真,取得了较好的效果,为基于神经网络优化的MoM仿真提供了一种新的思路。

本文提出了一种基于Adam的电大目标电磁求解技术,将矩阵方程的求解过程转化为神经网络模型参数优化过程。矩阵方程由行向量组成,每一个行向量视作一个训练样本,激励项向量视作数据标签。训练得到的网络参数即为原矩阵方程的解。由于每次训练过程中,仅随机选择部分样本进行网络参数训练,因此可以有效降低单次网络参数更新的计算复杂度,提升计算效率。

本文首先给出MoM求解电大目标电磁问题的积分算子和矩阵方程,然后建立一种矩阵方程的等效神经网络模型,并利用Adam对神经网络参数进行求解,最后通过数值算例验证本文方法的有效性。

1 MoM积分算子

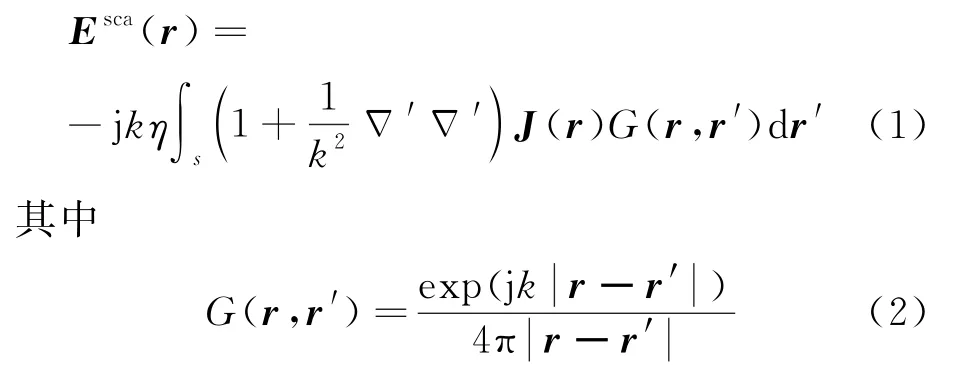
式中Δ:k为波数;η为波阻抗;s为电流源积分区域;′为对源点的梯度算符;J（·）为目标表面电流函数;G（r,r′）为自由空间格林函数,其中r,r′分别为场点和源点位置坐标矢量。对于目标表面未知的感应电流,通常采用离散单元上的局部电流基函数进行展开,然后代入式（1）,形成局部基函数展开的散射场。目标离散网格单元示意如图1所示。目标为双锥体结构,尺寸为0.254 m×0.051 m×0.051 m,采用三角形网格剖分,网格密度为0.003 m。

图1 目标离散网格单元示意图

选用RWG基函数作为展开函数,将目标上连续的感应电磁流离散为三角形面元上的局部基函数的线性组合,以分析目标的散射场。RWG基函数表达式为

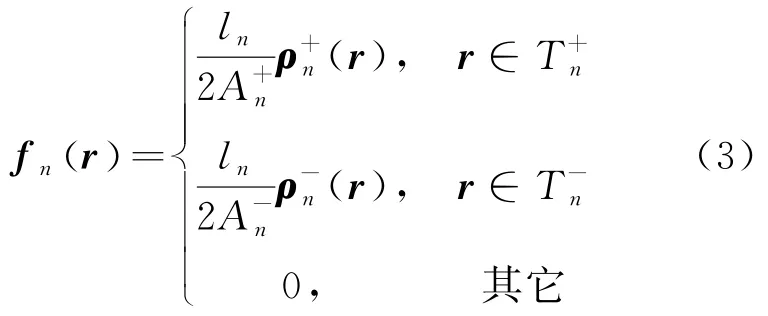
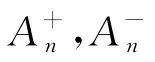
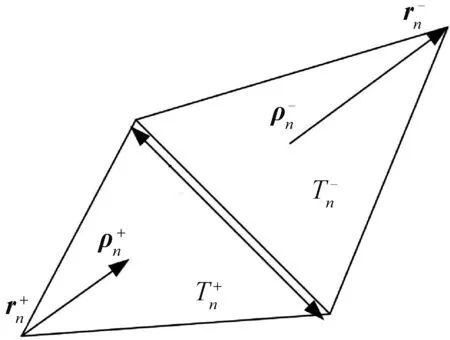
图2 RWG基函数示意图

假设外部照射平面波为E（r）=exp（jk·r）,k为传播矢量。根据金属表面边界条件,采用伽辽金（Galerkin）匹配方法,建立的矩量法矩阵方程为

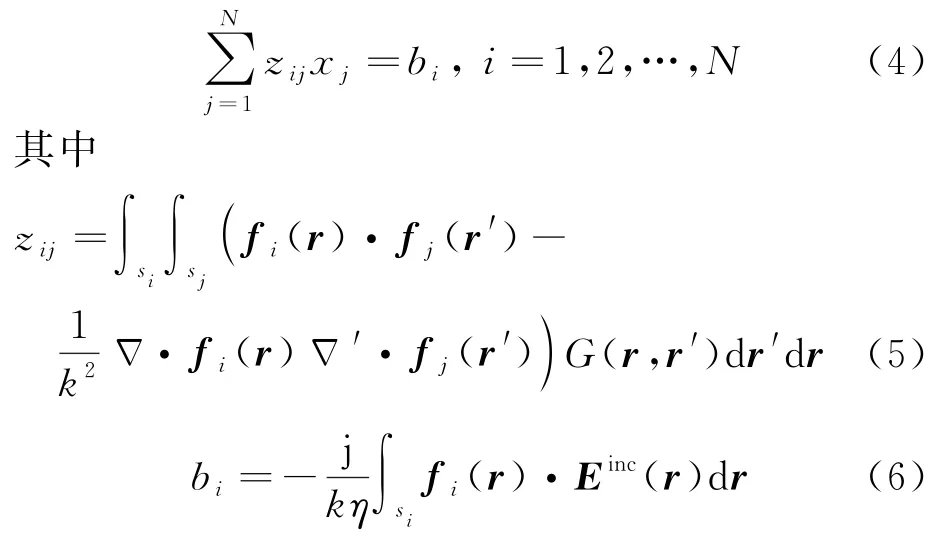
式中:N为基函数个数（一般为剖分网络单元的公共边个数）;z为矩量法阻抗矩阵第i行第j列的矩阵元素;x为感应电流在基函数上的展开系数;b为第i个激励项元素;f（·）,f（·）分别为第i个和第j个基函数;Δ为对场点的梯度算符;s,s分别为第i个和第j个基函数对应的积分区域。

根据式（4）,通过求解矩阵方程得到展开电流系数x,进而可得到目标表面的感应电磁流。由于RWG基函数要求离散网格密度不大于0.2λ（λ为电磁波波长）,对于电大目标通常会产生大量的未知数。为降低基函数数目,本文采用大面元上的相位提取（phase extraction,PE）基函数开展电流拟合,以降低计算复杂度。

采用PE基函数进行电流拟合,可以定义为

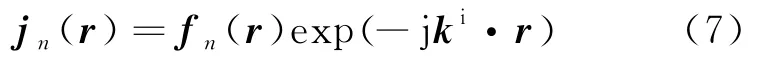
式中:k为入射电磁波矢量。将式（7）带入式（4）可得到相应的矩阵方程。相较于RWG基函数,PE基函数将变化剧烈的相位项单独提出,变化平缓的幅度项用RWG基函数描述,降低了对基函数离散网络密度的要求。对于平滑结构,PE基函数对目标的离散网格密度可达到0.5λ以上。

式中：σ为黑体辐射常数；εeff为腔体有效发射率；Tcav为吸收腔内表面温度；Ta为周围环境温度；εw为腔体内壁材料的热发射率。

2 矩阵方程的网络等效

MoM求解目标电磁问题的关键在于式（4）的计算。将式（4）中矩阵方差简化描述为

式中:Z为阻抗矩阵;x为系数矩阵;b为激励项矩阵。式（8）的求解可转化为代价函数的最小值优化问题,代价函数J（x）定义为

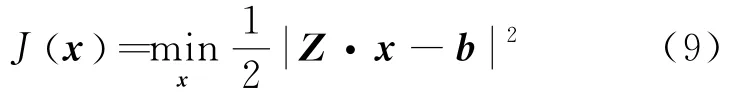
式中:min（·）为取最小值函数;|·|为求绝对值运算符。

针对该优化问题,建立等效神经网络预测模型,如图3所示。阻抗矩阵Z的每一行看作一个训练样本,网络模型实现矩阵向量乘运算。激励项矩阵b看作数据标签,待求系数矩阵x看作神经网络参数,训练得到的神经网络参数即为原矩阵方程的解。图3中,网络输出包含的两个元素b,b分别对应数值标签的实部和虚部;z,z分别为阻抗矩阵行向量z的实部和虚部;x,x分别为展开系数向量的实部和虚部;w-w分别为矩阵向量相乘得到的中间结果（复数矩阵分成实部、虚部后得到的实数向量）。对于式（9）的优化,应分别按照实部和虚部进行范数计算。通过梯度下降算法可获取网络参数,实现原矩阵方程的求解。

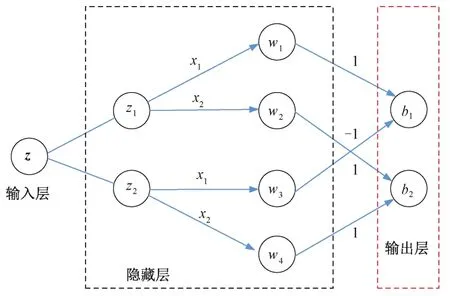
图3 等效神经网络预测模型

3 Adam求解算法

Adam是一种自适应更新步长的求解算法,通过自动调整梯度下降过程中的更新步长提升神经网络参数训练效率。Adam算法迭代求解公式为

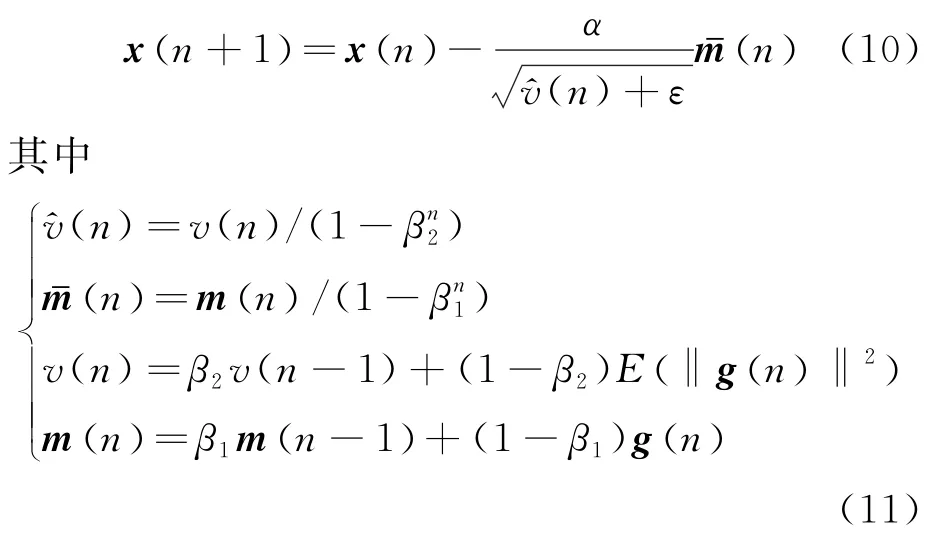
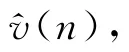
当更新步长α较大时,更新快,但不易收敛;当α较小时,更新慢。不同更新步长的收敛效果如图4所示。

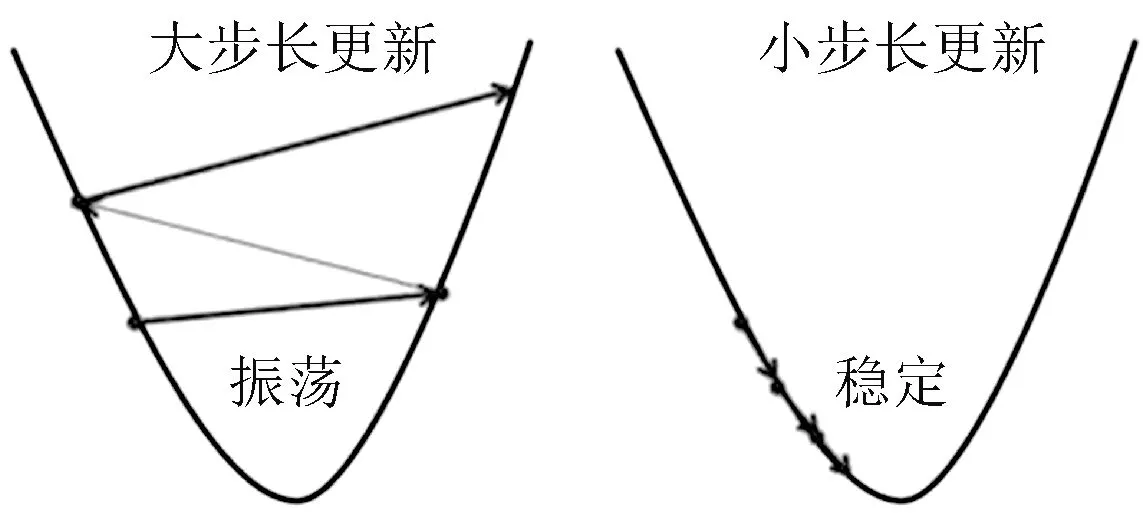
图4 不同更新步长的收敛效果

更新步长太大,则收敛很快,但在最优解附近易出现振荡;更新步长太小,则收敛很慢,而且易陷入局部最优解中。为解决该问题,本文采用的步长更新方程为

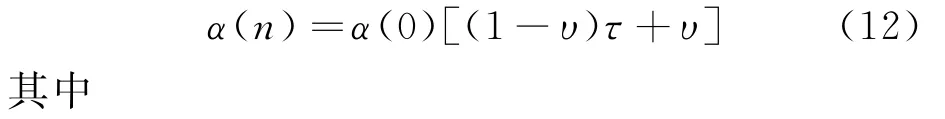
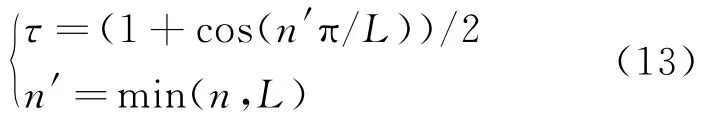
式中:α（n）为第n步的更新步长;α（0）为初始步长;υ为加权系数;τ为修正系数;n′为步长修正数目,用于控制更新步长大小;L为步数控制参数。当迭代步数大于L时,更新步长不再改变。

该策略可以将更新步长控制在有限的范围内。设α（0）=0.1,υ=0.5,L=70,更新步长余弦衰减曲线如图5所示。

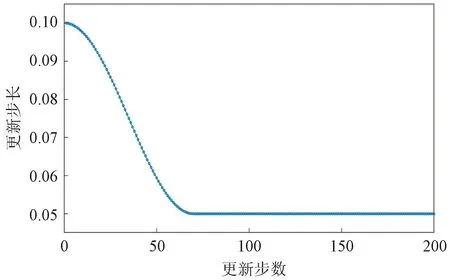
图5 更新步长余弦衰减曲线

利用Adam算法求解式（9）中的代价函数,可完成矩阵方程求解。根据式（10）,求解过程中,采用不同的迭代步数,随机地选择部分样本数据而不是全部数据,进行g（n）的计算,以降低单步求解复杂度。

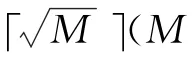
4 数值算例

在计算机（Intel i5-9600K@3.7GHz）上对图6所示的半径为5.0 m的金属球开展远场雷达散射截面积（RCS）仿真。采用平面波入射,频率为300 MHz,沿-x方向传播,y方向极化。散射扫描平面为x-y平面,方位角扫描间隔0.5°。通过与GMRES算法求解结果对比,验证Adam算法仿真精度和效率。

图6 金属球仿真示意图

不同求解算法得到的金属球RCS仿真结果如图7所示。各算法求解结果吻合较好,Adam算法求解得到RCS与Mie级数的均方根误差为0.53 dBsm,精度较高。

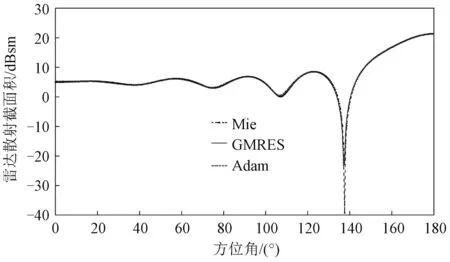
图7 金属球RCS仿真结果

图8给出了采用GMRES算法和Adam算法求解矩阵方程的误差收敛曲线,其中GMRES算法迭代步数20,耗时10.3 s,Adam算法（每次更新采用的样本数为904）迭代步数213,耗时7.1 s。

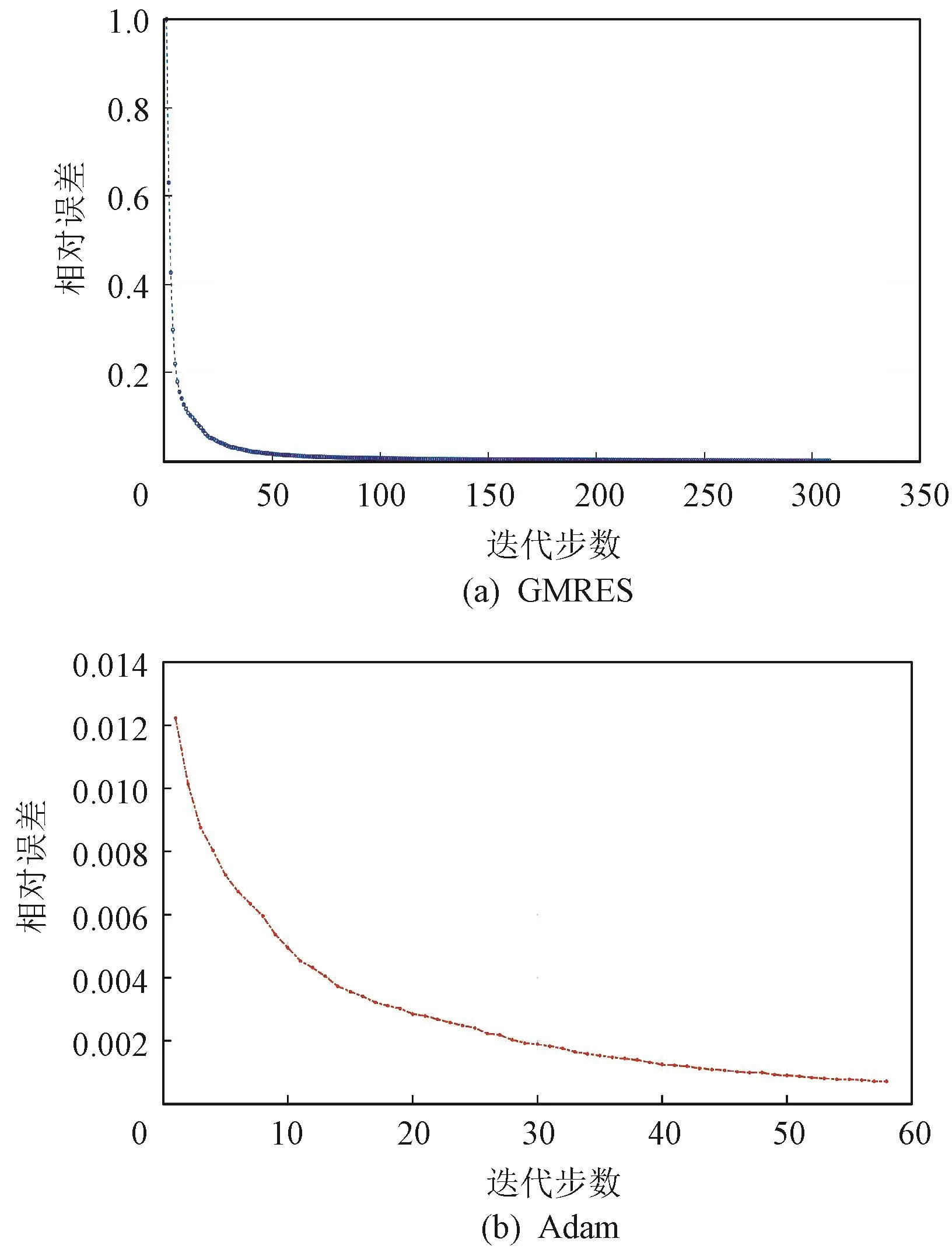
图8 不同算法迭代收敛曲线

对图9所示的边长为1 m的金属立方体开展RCS仿真。平面波照射频率为3.0 GHz,入射角度为俯仰90°、方位0°,水平极化;散射扫描角度为俯仰90°、方位0°～180°,扫描间隔0.5°。

图9 立方体仿真模型

采用传统RWG基函数的网格数为132 192,采用PE基函数的网格数为3 168,采用 MoM形成的阻抗矩阵维度缩减为传统RWG阻抗矩阵维度的0.05%。以RWG基函数仿真结果为参考,采用Adam算法求解PE基函数生成的矩阵方程,单步更新样本数为1 584。不同方法求解立方体RCS和感应电流系数的仿真结果如图10所示。

图10（a）给出了采用RWG基函数离散目标,利用GMRES算法求解矩阵方程得到的RCS仿真结果,与本文所提方法求解仿真结果的对比曲线,均方根误差为1.3 dBsm,仿真结果吻合较好。产生误差的主要原因是Adam算法基于历史梯度信息对更新方向进行修正,而GMRES算法通过修正子空间上的全局梯度信息进行更新,在预设阈值下存在一定偏差。图10（b）给出了采用PE基函数离散目标,分别利用GMRES和Adam求解矩阵方程得到的目标表面感应电流系数,实部均方根误差为-70 dB,虚部均方根误差为-58 dB,两者吻合较好。其中阻抗矩阵条件数为259.9,GMRES迭代81步后相对误差为0.009,耗时13.2 s,Adam迭代212步后相对误差为0.01,耗时5.6 s。

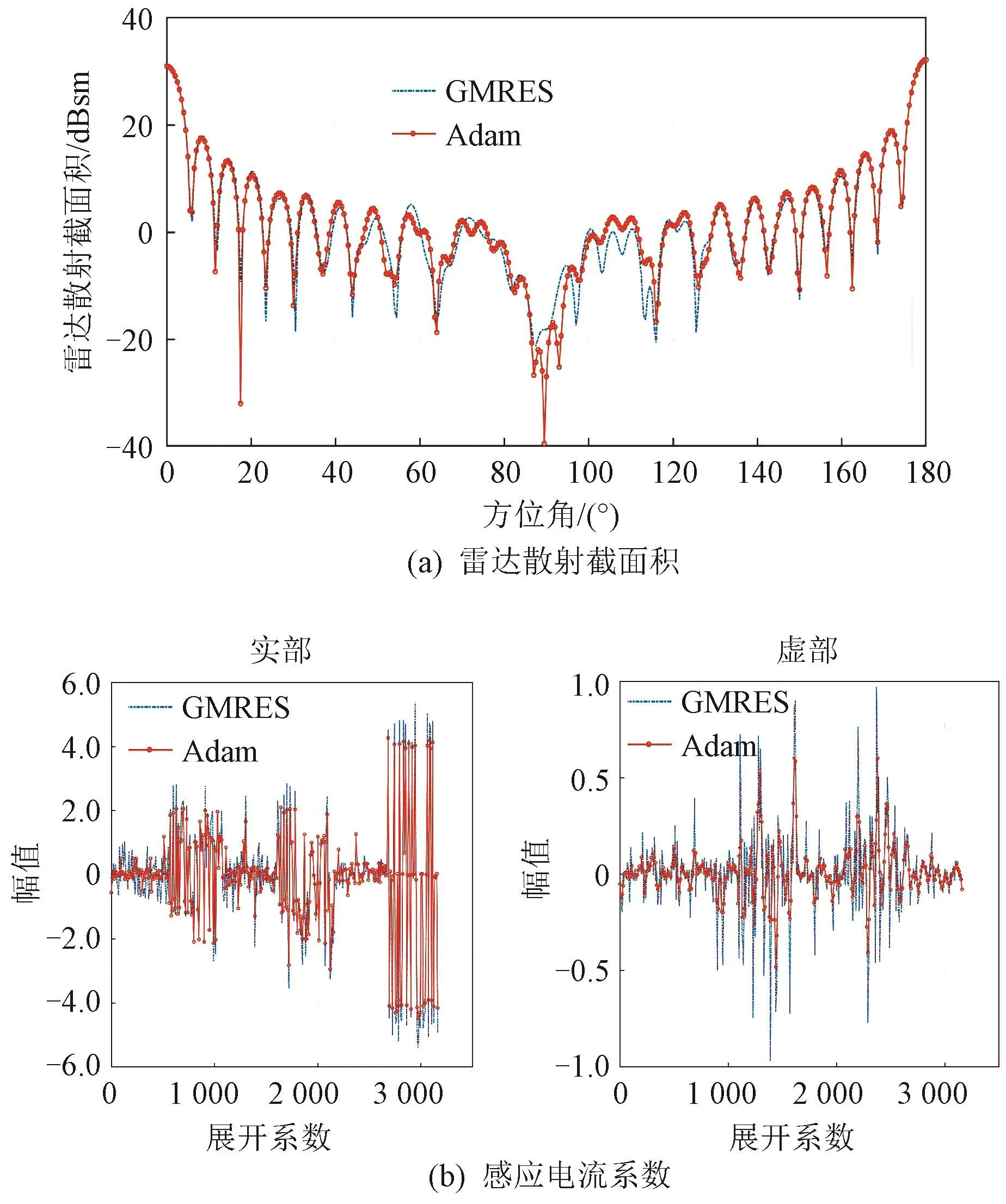
图10 不同方法求解立方体RCS和感应电流系数的仿真结果

5 结论

本文提出了一种基于Adam的电大目标电磁场快速求解方法。首先利用大离散单元上的PE基函数有效降低MoM阻抗矩阵维度,然后将矩阵方程求解转化为代价函数的最小值优化问题,最后设计一种神经网络模型,训练得到的网络权值即为原矩阵方程的解。网络训练过程中Adam算法的梯度和二阶矩的更新仅采用部分数据开展计算,降低了单步求解计算复杂度。数值仿真验证了本文所提算法的有效性。