混合动力重型货车参数局部与集成优化仿真研究

2022-10-12杜常清何隽逸杨贤诚

汽车工程学报 2022年5期

杜常清，何隽逸，张佩，杨贤诚

（1.武汉理工大学现代汽车零部件技术湖北省重点实验室，武汉 430070；2.武汉理工大学汽车零部件技术湖北省协同创新中心，武汉 430070；3.湖北省新能源与智能网联车工程技术研究中心，武汉 430070）

近年来，随着我国现代化基础建设的不断发展，中重型载货汽车的保有量稳步增长，消耗了大量的石油，是交通运输中大型CO排放源之一。为了保证汽车行业的可持续发展，并响应国家能源战略需求，重型商用车的节能减排显得十分重要。同时针对重型货车日益严格的油耗需求和排放限值，使传统重型货车难以兼顾经济性和动力性需求，研究并发展新型高效混合动力重型货车迫在眉睫。选择合适的动力源参数、建立高效的能量管理策略是混合动力汽车研究的核心重点。动力源参数对于提高经济性和降低成本非常重要，能量管理策略对保证获得最佳动力性和经济性、最低排放起着决定性作用。因此，混合动力重型货车的最优参数设计需融合动力源参数匹配、能量管理策略两方面的研究成果。目前，混合动力汽车参数优化分为动力源参数局部优化、控制参数局部优化以及动力源参数与控制参数集成优化。

混合动力重型货车运行模式较为复杂，工程实际中考虑到能量管理策略的可实施性，目前采用较多的仍是基于规则的能量管理策略。基于规则的控制策略通过设立车速、需求转矩、发动机特性曲线、电池荷电状态（State of Charge，SOC）等逻辑门限值，使汽车在运行时，能够实时合理分配电机与发动机转矩，发动机工作在高效区时长增加，从而节省燃油。但其门限值的确定需进行大量参数标定工作，工程量大且效率低。基于此，国内外学者对其门限值中的部分关键参数采用优化算法自动寻优。李萍等应用粒子群优化算法对规则控制中的荷电状态和发动机最优工作区间等3个阈值参数在可控范围内进行寻优，取得了更好的燃油经济性。CHEN Zheng等应用遗传算法优化发动机启动功率阈值，发动机工作在高效区的时长增加，从而提高了燃油经济性。邓元望等应用混沌遗传算法对隶属函数和控制规则进行优化，克服了遗传算法局部收敛的缺陷，提高了燃油经济性，并降低了CO排放量。

当混合动力重型货车的能量管理策略确定后，其动力源参数与控制策略参数相互耦合，共同影响着混合动力车辆的综合性能。混合动力汽车参数优化也由最初单一的动力源参数优化或控制系统参数优化过渡形成两者的集成优化。邓涛等以燃油经济性为优化目标，以动力性能为约束条件，采用非支配排序遗传算法（Non Dominated Sorting Genetic Algorithm-II，NSGA-II）对PHEV的传动系参数和能量管理控制参数进行了优化，与优化前控制策略进行仿真对比，燃油经济性提高了7.8%。刘建辉等以动力系统参数和能量控制策略参数为优化变量，以油耗和有害气体排放量为优化目标，采用交叉-变异蜂群算法进行参数优化，得到了更高效的参数全局搜索方式。李垚以经济性和动力性为目标，对单轴并联式HEV动力源参数进行了优化，得到局部最优匹配结果；接着耦合控制参数，将控制参数与动力源参数集成优化，进一步提升了整车燃油经济性。

以上研究大多通过智能算法单一优化动力源参数或控制策略参数，并将得出的局部优化参数下的经济性与原始初值参数下的经济性进行对比，或集成优化出全局动力源参数、控制策略参数下经济性与原始初值参数下的经济性进行对比，并未进行局部优化结果与全局优化结果的相互对比。特定车型在特定的行驶工况下运行，其全局优化参数后的经济性并不一定优于局部优化参数的结果。针对上述研究存在的不足，本文建立了可缩放整车动力学模型，采用粒子群算法对关键动力源参数进行了局部优化；基于发动机高效工作区和SOC，设计了基于规则的能量管理策略，采用粒子群算法（Particle Swarm Optimization，PSO）对规则中部分重要逻辑门限参数值进行了局部优化；联立整车模型和控制策略模型，对关键动力源参数和控制策略参数集成优化，得到全局优化参数后的整车经济性，并与前述两次局部优化结果进行对比分析，探究了混合动力重型货车在特定工况下参数局部优化与全局优化结果的优劣性。

1 可缩放整车动力学模型及动力源参数优化

1.1 整车结构

本文选取P2构型的混合动力重型货车作为研究对象，单轴并联混合动力系统依次由发动机、离合器、驱动电机、动力电池、AMT变速器、主减速器等组成，其结构如图1所示，主要部件参数见表1。

表1 整车基本参数

图1 P2构型结构简图

1.2 基于Matlab的整车模型构建

针对混合动力系统动力源参数与控制策略参数集成优化研究，基于Matlab/Simulink软件，采用前向仿真方法，搭建了单轴并联式P2构型混合动力货车的发动机模型、电机模型、整车纵向动力学模型、电池模型等。

1.2.1 整车纵向动力学模型

本文重点研究重型货车动力源参数和控制参数的集成耦合，忽略横向和垂向动力学对车辆的影响，仅考虑纵向的动力学特性，且忽略车轮与地面的滑移。作用在驱动轴的驱动力矩和制动力矩使车辆加速或减速，车辆驱动时有：

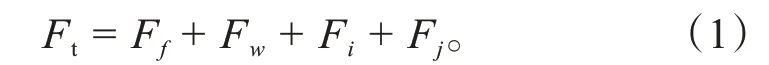
车辆制动时有：

式中：为整车驱动力；F为滚动阻力；F为坡道阻力；F为空气阻力；F为加速阻力；为电机制动力；为机械制动力；为车辆质量；为轮胎滚动阻力系数；为坡度，仿真中设置为0；ρ为空气密度；为空气阻力系数；、为车速，单位分别为km/h、m/s；A为迎风面积；为旋转质量换算系数。

整车需求转矩为：

式中：为驱动转矩；为总传动比；η为传动系统效率；为车轮半径，m；为行驶时整车需求转矩，Nm。

1.2.2 发动机Willans Line模型

Willans Line模型的可缩放性使其非常适合于混合动力系统参数优化匹配的仿真分析。根据Willans Line理论，发动机实际输出能量与输入能量存在如下关系：

式中：斜率为发动机能量转换效率的峰值；为输入发动机总能量；为转换后输出的总能量；截距为发动机内部损耗。

对于发动机，存在如下关系式：

式中：为发动机输出有效转矩，Nm；̇为发动机燃油质量流量，kg/s；为发动机燃油低热值，J/kg；为发动机当前转速，rad/s。

基于上述公式，发动机有效效率可表示为：

Willans模型采用平均活塞速度u和平均有效压力两个正则化变量来描述发动机工作特性。使用正则化变量的最大优点在于，对于所有发动机，它们的范围是基本相同的，而与发动机尺寸无关，以四缸发动机为例，公式如下：

式中：为发动机排量，L；为活塞冲程，mm；为平均可提供压力。

因此有：

式中：为平均损失有效压力。

由此可知，对于发动机效率计算而言，关键是获取发动机能量转换效率和平均损失压力，和是与发动机转速和转矩有关的函数，可根据发动机特性试验获得。缩放后的发动机转速-转矩外特性曲线则根据现有机型外特性曲线进行缩放估算。

1.2.3 电机模型

混合动力系统动力源参数优化和能量管理策略研究关注的是循环工况长时间段内系统的燃油消耗，因此不考虑电机的电磁学以及热力学等动态特性，不考虑其内部复杂的转换关系。搭建电机试验台架，整理试验数据，以此建立电机的准静态模型。电机外特性曲线图以及效率MAP图，如图2所示。

图2 电机效率MAP图

驱动电机实际输出转矩与驱动电机和动力电池组特性有关，电机输出功率与电功率在不同工作模式下的计算方式不一，如下式所示。

驱动状态电机功率：

发电状态电机功率：

式中：和分别为电机的输出功率和电功率；为当前电机效率。

由于线性扩展模型简单方便，非线性扩展模型复杂、计算量大且线性扩展模型与非线性扩展方法得到的结果相差不大。电机的参数优化匹配采用线性扩展方法，首先确定电机基准部件参数值，同时根据电机试验台架数据确定基准特性曲线，再基于扩展后电机部件参数值相对基准部件参数值的变化进行等比例修改基准特性曲线，从而得到扩展后的电机特性曲线。本文假定电机效率不变，电机转矩依据其参考机型转矩，与参考机型最大功率呈线性比例，如式（18）所示。

式中：和分别为电机参考机型转矩和最大功率，单位分别为Nm和kW；为驱动电机目标机型最大功率，kW。

1.2.4 电池模型

本文不考虑电池在充放电过程中的化学特性，忽略温度对动力电池性能的影响，采用常见的等效电路Rint模型，等效电路模型如图3所示。

图3 动力电池模型

公式如下：

式中：()为电池开路电压，V；()为电池电流，A；()为电池组功率，kW；()为电池内阻，Ω。

电池组的SOC表示电池组剩余电量与额定容量的比值，如下式计算：

式中：为电池容量，Ah。

1.3 基于粒子群的动力源参数局部优化

在动力源参数优化设计过程中，正确地选择寻优参数是优化设计的第一步，选择的参数变量需要对其动力部件特性具有重要影响，同时其在更新变化过程中，对应的部件特性曲线能够相应更新变换。功率变量作为电机以及发动机的关键参数，其变化对整车动力性以及经济性有显著影响，同时当功率参数改变时，电机、发动机外特性曲线随之规律变化。因此，选取发动机功率，电机功率作为设计变量，能量管理策略采用下述基于规则控制策略，优化区间见表2。

表2 动力源优化参数取值区间

式中：为发动机最大功率，kW；P为电机最大功率，kW。

PSO作为群体算法的一种，是人类受益于动物的行为创造的一种静态全局最优算法。动力源参数中的两个功率因子优化问题属于非线性最优搜索问题，适合应用PSO来优化，其优化流程如图4所示。

图4 基于PSO优化动力源参数流程

首先，种群初始化，设定粒子群的粒子数=10。粒子在寻优范围内随机初始化一群粒子，此时粒子的初始位置即为个体最优位置P的初始值，初代粒子中最优位置为G的初始值。每次迭代时，将该代粒子位置作为输入量，代入模型层仿真计算出对应的适应度值函数()，结果交互到算法层进行对比寻优出这一代的个体最优位置与群体最优位置，然后通过如下速度和位置的更新公式不断迭代寻优40代，得到收敛的群体最优位置。

式中：为初始惯性权重值，取0.9；为优化终止惯性权重值，取0.4；为最大迭代次数，取40代；为当前迭代次数。

为了防止粒子盲目搜索导致超出寻优范围，将粒子寻优速度和位置约束在[-，]和[-，]范围内。在C-WTVC工况下对两功率参数进行寻优，其参数优化变量与适应度函数的迭代过程如图5～7所示。

图5 适应度目标函数变化曲线

可以看出，当迭代步数到大约第10代时，功率变量与目标函数开始收敛于最优解，符合收敛速度和精度的要求。各子图中，蓝色连线为种群中所有粒子参数在40代迭代过程中的变化曲线，红色连线则为每一代中种群最优适应度值（油耗经济性最低）所对应粒子参数值的连线。从粒子群优化后的结果来看，当功率参数值=270.67 kW，=206.55 kW时，最后的适应度值油耗最小，油耗优化结果达到局部最优。

图6 Pc值变化曲线

图7 Pm值变化曲线

2 改进规则的能量管理策略

2.1 基于规则的能量管理策略设计

基于规则的能量管理策略因其反应迅速、工程易实现的优点，成为商业化整车控制器中应用最多的控制策略。其规则的制定，核心是找到发动机高效的工作区间，通过大量标定试验得到的最佳参数阈值，如电池SOC阈值（电池放电停止阈值SOC、电池充电停止阈值SOC、电池稳定阈值SOC）及实际需求转矩，结合电机调节发动机的输出转矩，制定相应的转矩分配策略，提高发动机的工作效率，从而提高系统的能量效率。

图8为发动机转速-转矩工作区间，发动机峰值转矩曲线为台架试验测得的外特性曲线，即发动机各单位转速下峰值转矩值拟合而成的曲线；发动机最优输出转矩曲线是由发动机每个转速下的有效燃油消耗率最低点所对应的发动机转矩值拟合曲线；发动机启动转矩曲线是发动机工作时燃油消耗较高的曲线，低于此曲线时关闭发动机。

图8 发动机工作区间

根据上述发动机工作区阈值和电池SOC上下阈值将行驶模式分为纯电动模式、发动机单驱模式、电机助力模式以及行车充电模式。

（1）纯电动模式：车辆需求转矩小于发动机最小转矩线且电池SOC大于电池放电停止阈值SOC。

（2）发动机单驱模式：车辆运行中等负荷，发动机工作在最优输出转矩线附近区域，燃油消耗率低，燃油经济性好。

（3）电机助力模式：当需求转矩大于发动机最优输出转矩同时小于发动机峰值转矩时，使发动机输出最优转矩曲线，电机补偿剩余转矩；当需求转矩大于发动机峰值转矩时，使发动机输出外特性转矩曲线，电机补偿剩余转矩。

（4）行车充电模式：如果需求转矩小于发动机启动转矩，且电池SOC小于电池放电停止阈值SOC，发动机对外输出启动转矩，过量转矩供给电机发电；如果需求转矩大于启动转矩，小于最优输出转矩，且电池SOC小于电池充电停止阈值SOC，发动机输出最优转矩曲线，过量转矩分配电机发电；如果需求转矩大于最优输出转矩，但小于峰值转矩，且电池SOC小于电池放电停止阈值SOC，发动机则输出峰值转矩。

根据上述规则，设计出基于规则的控制策略，切换条件见表3。

表3 驱动工作模式切换规则

2.2 基于粒子群优化阈值的规则策略

由于发动机的运行具有非线性，规则的制定缺乏科学的数学计算分析与理论基础，工程实际制定时需基于给定的车辆结构与工况循环进行反复的标定测试。发动机外特性曲线可通过专业的发动机试验台架测得，但其最优输出转矩曲线及启动转矩曲线的逻辑门限值与规则难以得到。同时电池荷电状态阈值往往也取决于工程人员的经验，具有主观臆测误差。可见，电池荷电状态阈值（电池放电停止阈值SOC、电池充电停止阈值SOC）、发动机最优输出转矩曲线、发动机启动转矩曲线都是影响规则控制效果的关键因素。由于输出转矩曲线不便参数化进行寻优，对其设置比例因子，转而对其比例因子进行参数优化。最终，使用粒子群优化算法对规则控制中的4个阈值SOC、SOC、最优输出转矩因子opt、启动转矩因子start在可控范围内进行寻优，优化变量范围见表4。

表4 控制策略优化参数取值区间

控制策略参数优化流程与上述动力源参数优化流程一致、粒子群参数的设置也与上述保持一致，仿真工况选择C-WTVC工况，与上述保持一致。算法执行后的每代最优粒子参数位置结果如图9所示，其对应的最优适应度函数曲线如图10所示。

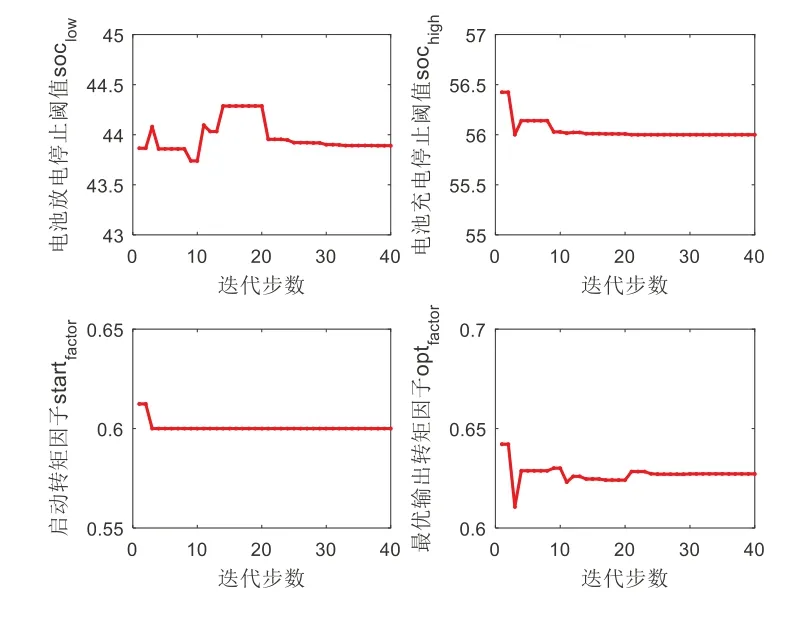
图9 规则策略关键参数优化过程

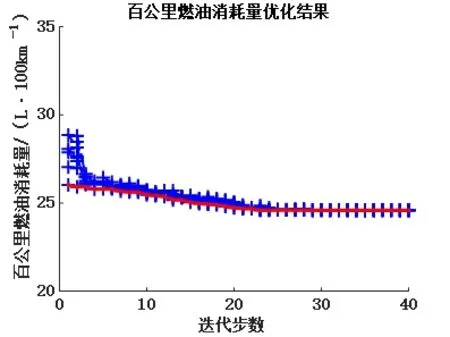
图10 适应度值优化曲线

3 动力源参数与控制策略参数集成优化

前文分别介绍了在固定的控制策略参数下进行并联混合动力重卡动力源参数优化匹配，以及在固定的动力源参数下进行并联混合动力重型货车控制策略参数优化匹配。上述采用串行优化的方法，分别得到了局部最优的动力源参数、控制策略参数以及对应的油耗适应度值，但对于整车而言，动力源参数和控制策略参数是耦合的。因此，需将动力源参数与控制策略参数集成在一个搜索空间，进行并行优化，得到全局最优的集成参数优化结果以及相应的油耗适应度值，再将局部与集成优化的仿真结果进行对比分析。

将上述动力源参数与控制策略参数集成为一个搜索空间，修改粒子群算法，增加其空间维数至6维，设置各参数不同的寻优速度。不同参数其寻优空间范围不同，寻优速度则需不同，合适的寻优速度能保证各参数粒子不会过早出现局部收敛、防止粒子远离目标区域等。同样采用CWTVC工况，以整车动力性能为约束条件，油耗经济性为目标函数进行集成优化，并与之前局部优化结果进行对比，分析二者的差异。参数集成优化过程如图11所示。

图11 集成参数优化结果

由表5可知，动力参数局部优化、策略参数局部优化与原型车相比，油耗优化结果分别降低4.25%、3.19%。参数集成优化后的油耗相对于参数局部优化后的油耗降低了11.4%、12.4%，相对于原型车降低了15.2%。集成优化在原型车的基础上增大了发动机启动转矩因子start，扩大纯电动模式区间，为维持SOC稳定在充放电阈值区间，集成优化后的电机最大功率相对提高，电机助力性能更强，在保证动力性的前提下，优化后的发动机最大功率随之减小，油耗值下降。

表5 局部优化与集成优化匹配结果比较

将优化后的全局最优参数结果应用于整车缩放模型和规则策略模型中，得出各动力部件实际转矩之和与整车需求转矩、实际车速与目标车速对比曲线如图12所示，验证优化参数结果对模型的适配性。

图12 转矩对比、车速跟随图

蓝色实线代表整车需求转矩以及目标车速，红色虚线代表各动力部件实际输出转矩之和以及实际车速。从图中可以看出，优化得到的参数应用于本文建立的整车缩放模型和规则策略模型，在CWTVC标准工况下，能够使实际车速与目标车速跟随基本吻合，动力部件实际输出转矩之和与整车需求转矩相差较小，验证了所选参数对模型的适配性。同时为了避免在不同参数下SOC变化过大对评价发动机油耗结果的影响，代入3次参数优化结果，得到SOC变化曲线如图13所示。

图13 SOC变化曲线

由图13可知，初始SOC均设为50%，代入不同参数优化结果后，工况终止时终止SOC分别稳定在54.97%、54.75%、53.98%。终止SOC相差在1%之内，可忽略其对发动机油耗结果造成的影响。综合上述结果证明在该特定工况下，混合动力重卡通过动力系统参数和能量管理策略参数的集成优化与原型车、局部优化相比能进一步实现油耗降低的目标，得到全局最优结果。