多元非线性数学模型在碳纤维纸拉伸强度预测中的应用

孟建梅，王晓丽

（1.晋中职业技术学院，山西 晋中 030600；2.晋中学院，山西 晋中 030619）

0 引言

近年来，世界各国都在积极开发并应用新型清洁能源，目前燃料电池作为第四代发电技术，单位重量输出的电能大、功率大，在军用和民用等领域均具有较大的应用前景，故进行相关课题的开发和研究非常重要。碳纤维纸是燃料电池中的重要组成部分之一，作为燃料电池气体扩散层的基底材料发挥重要作用［1］，直接关系到燃料电池燃料的利用率，碳纤维纸的拉伸强度关系到气体扩散层中膜电极安装的稳定性，关系到电池使用寿命［2］。基于此，对碳纤维纸拉伸强度进行预测具有重要的现实意义。

目前我国部分学者已经获得一定的研究成果，文献［3］中建立了高温环境下碳纤维增强聚丙烯复合材料拉伸强度的预测模型。为研究复合材料的断裂机理，进行拉伸试验，观察断口形貌，然后选择Duva-Curtin-Wadley模型作为纤维断裂判据，将其纳入等效夹杂模型，结合Mori-Tanaka理论预测老化行为与失效情况，该方法虽然可对拉伸强度进行预测，但预测精度不佳。文献［4］中通过对力学参数进行标定实验获得75组有效数据，由此构建了基于小样本数据的传统多元回归方程、典型前馈式及反馈式神经网络等不同预测模型，对模型的不同拟合效果和预测精度进行分析，再选用遗传算法对最优的预测模型进行优化，以此实现对材料拉伸强度的预测。该方法虽然试验成本较低，运算复杂度不高，但由于它是以胶脂为研究对象，在对碳纤维纸的拉伸强度进行预测时仍然存在预测精度较低的问题。

基于前人研究经验，本文基于多元非线性数学模型构建一种预测模型，并将它应用到碳纤维纸拉伸强度预测当中。

1 基于多元非线性数学模型的强度预测模型构建

碳纤维纸的功能是保护膜电极集合体并传导电流［5］。其位置如图1所示。

图1 碳纤维纸在燃料电池中的位置示意图

碳纤维纸的独特作用对其性能有着极高的要求，高抗拉强度就是其中之一［6］。为明确碳纤维纸的使用寿命，确定其失效机理，本文基于多元非线性数学模型建立一个预测模型，对碳纤维纸拉伸强度进行预测。首先筛选碳纤维纸拉伸强度的影响因素，而后基于多元非线性数学模型建立影响因素与拉伸强度之间的关系模型［7］。

1.1 碳纤维纸拉伸强度影响因素筛选

多元非线性数学模型预测原理是以自变量的变化来推断因变量的变化，因此建立预测模型的前提条件是确定模型的自变量，也就是筛选与之息息相关的影响因素。目前影响因素筛选方法主要有两种，一是GM（1，1）模型法，二是主成分分析法［8］。在这里，采用前一种进行影响因素筛选。下面对该方法筛选过程进行具体分析。

步骤1：收集资料，罗列可能对碳纤维纸拉伸强度产生影响的因素。这一环节罗列的影响因素越全面越好［9］。

步骤2：对罗列出来的影响因素进行整理，并重新排列组合。

步骤3：建立参考数列，即所有比较数列的对比标准，其形式如下：

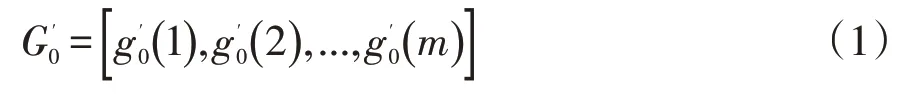
式中，m为指标的个数。

步骤4：建立比较数列，它是由实际选出的所有影响因素构成，其形式如下：

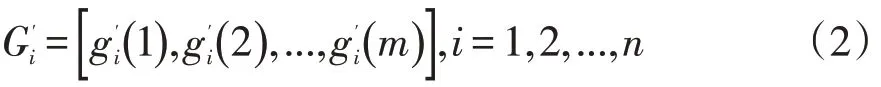
步骤5：按照公式（3）对所有影响因素进行无量纲化处理。

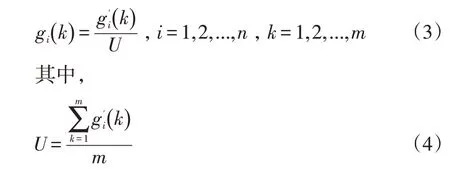
步骤6：计算比较数列与参考数列中各个影响因素的差值P，并进行绝对化处理［10］。公式如下：

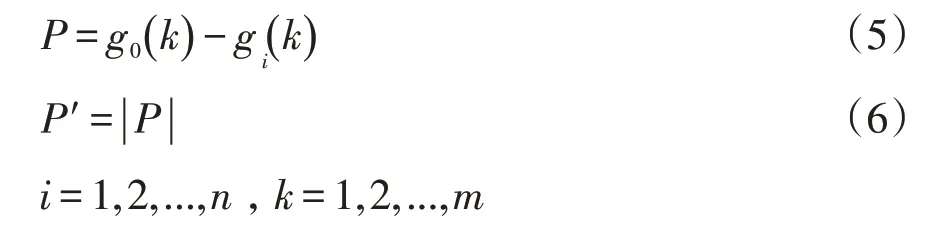
式中，P′为绝对差值，n为影响因素的数量。

步骤7：从计算出来的P′值中选出最大值p′max和最小值p′min。

步骤8：按照公式（7）计算各个影响因素的关联系数ζi(k)，数学表达式如下：

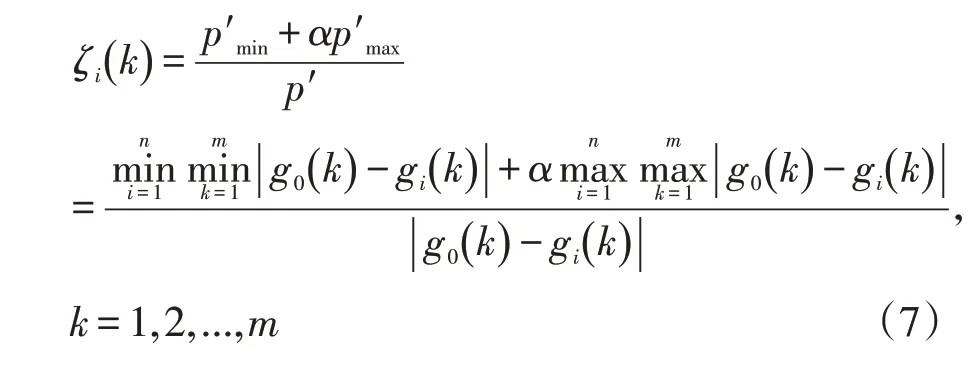
其中，α为分辨系数，0<α<1，一般情况下，取中间值0.5。

步骤9：将关联系数集中为一个值，也就是计算数列关联度β0i。计算公式如下：

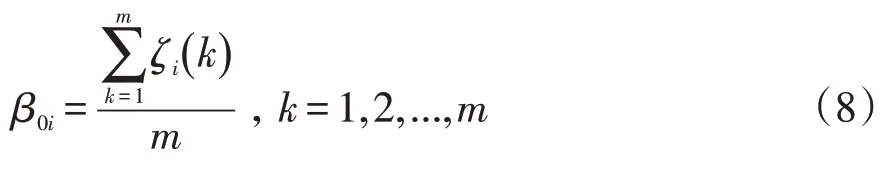
步骤10：关联度排序，选取前n个影响因素作为影响碳纤维纸拉伸强度的主要因素。

1.2 强度预测模型构建

预测是指以一些已知数据来推断未知数据的过程。本研究以已知的碳纤维纸拉伸强度影响因素来预测碳纤维纸拉伸强度这一因变量数值发生变化的情况。二者具有很强的关联性，因此在这里引入多元非线性数学模型来构建二者之间的关联预测模型［11］。下面进行具体分析。

多元非线性数学模型一般形式如下［12］：

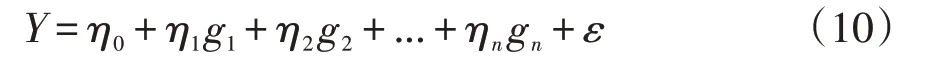
式中，η0,η1,...,ηn是n+1个待估参数；η0称为回归常数；η1,...,ηn称为回归系数；Y为因变量（碳纤维纸拉伸强度），g1,g2,...,g n为自变量（影响因素）；ε为随机误差。

（1）若给出了式中各个待估参数η0,η1,...,ηn的明确数值，记为，而ε则不再具有意义，因此公式（10）写为

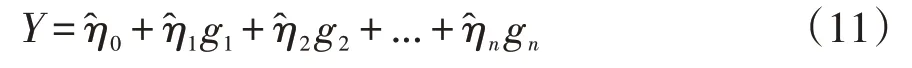
上述公式则不再称为多元非线性数学模型，而是称为多元经验回归模型。

（2）若给定一组自变量（影响因素）g1,g2,...,g n，则可以得到一个Y值，记为，̂就是Y的一个预测值。这时随机误差ε常常假定为

式中，e为常数。

（3）若已获得N组观测数据(gi1,g i2,...,gin;Y i)，i=1,2,...,n，则公式（10）写为

那么多元非线性数学模型就可以写成如下的形式：

式中，G T为G的转置。

2 碳纤维纸拉伸强度多元非线性预测模型应用分析

为检验多元非线性预测模型在碳纤维纸拉伸强度预测中的应用效果，通过实验的方式来获取N组碳纤维纸拉伸强度影响因素数据，然后以此为依据进行未来变化趋势预测，检验模型的预测准确性［14］。

2.1 研究对象选择

本文选择的研究对象为一种高性能碳纤维纸TGP-H-060，该碳纤维基本参数如表1所示。

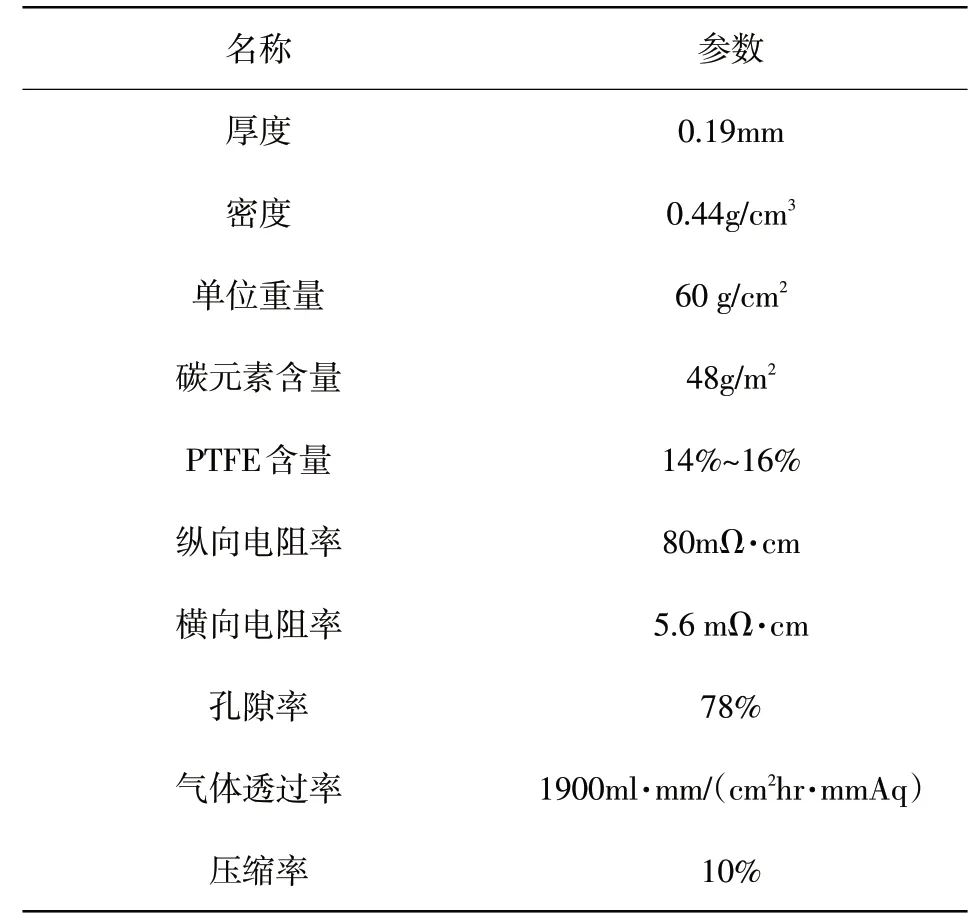
表1 TGP-H-060高性能碳纤维纸基本参数

2.2 影响因素筛选结果

结合TGP-H-060高性能碳纤维纸生产工艺以及生产环境，利用1.1的方法筛选对其拉伸强度有着明显影响作用的因素，最终筛选出关联度大于3的影响因素作为关键因素，结果如表2所示。

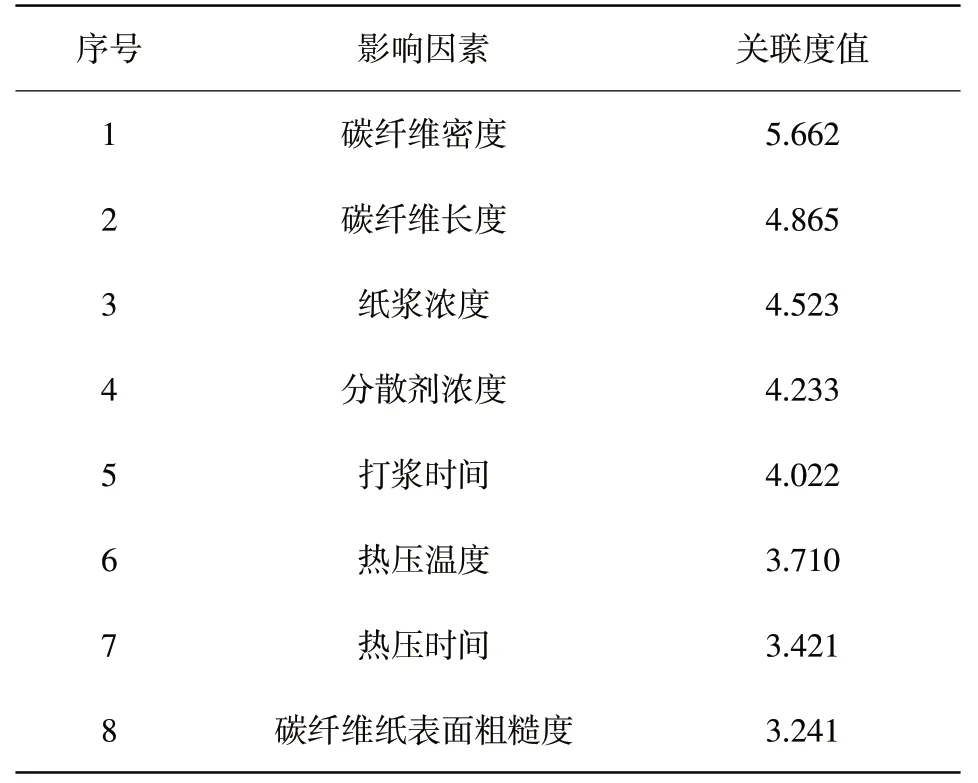
表2 TGP-H-060高性能碳纤维纸影响因素表

2.3 碳纤维纸拉伸强度测试设备

选取PY-H801电子拉力试验机来测试纸张在恒速拉伸条件下的拉伸强度变化情况［15］。PY-H801电子拉力试验机基本技术参数如表3所示。

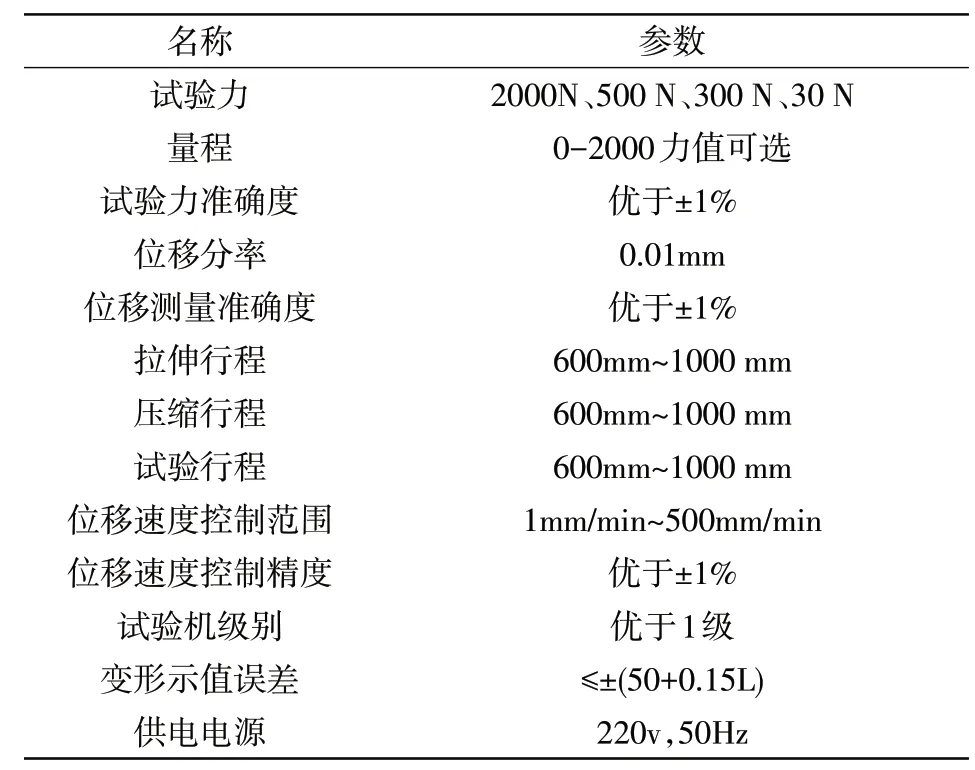
表3 PY-H801电子拉力试验机基本技术参数

2.4 碳纤维纸拉伸试验环境

将TGP-H-060高性能碳纤维纸裁剪成长度250mm、宽度15mm的试样，将试样放置到PY-H801电子拉力试验机上，随后向相反方向做拉力运动，采集这一过程中的力值和位移，以此计算拉伸强度值，如图2所示［16］。

图2 碳纤维纸拉伸实验示意图

2.5 观测数据集

PY-H801电子拉力试验机工作下，获取得到10组影响因素值和碳纤维纸拉伸强度值，如表4所示。

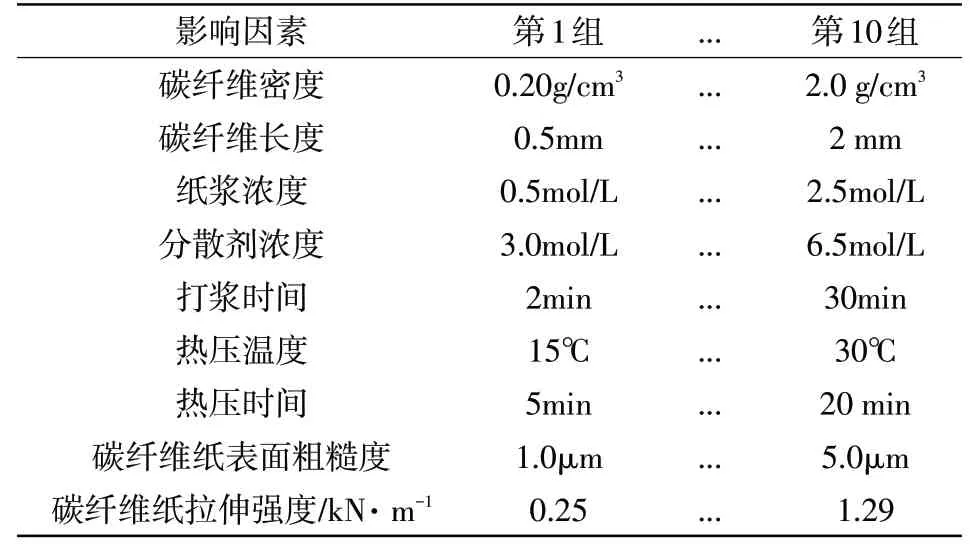
表4 观测数据集

2.6 参数η0,η1,...,ηn估算与检验

以得到的前7组观测数据为已知数据，输入到式（11）当中，利用最小二乘法来计算模型当中的η0,η1,...,ηn值，并进行假设检验，结果如表5所示。

表5 回归系数及其模型检验结果

根据表5，建立碳纤维纸拉伸强度预测模型如下：

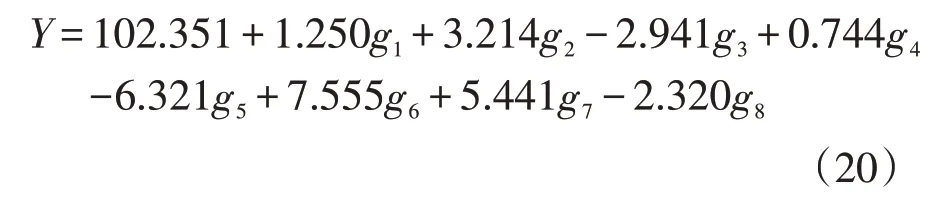
2.7 估测准确性检验

以表4后3组数据中的影响因素为准，利用公式（20）预测相应的碳纤维纸拉伸强度值，并与实际值进行对比，结果如表6所示。

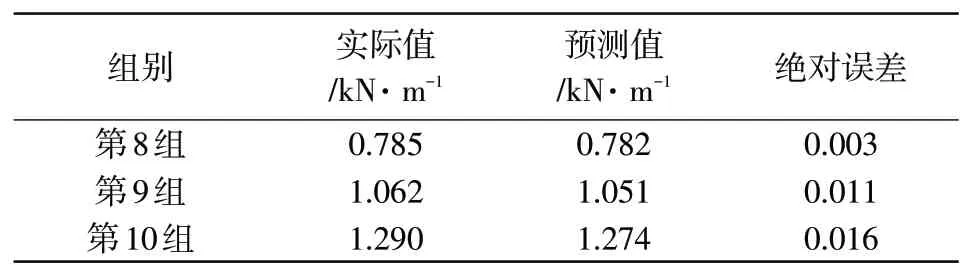
表6 估测准确性检验结果

从表6中可以看出，利用所构建的基于多元非线性数学模型的预测模型对碳纤维纸拉伸强度值进行预测，所得预测值与实际值之间的误差小于1 kN·m-1，说明该模型的预测准确性较高，具有广泛的应用前景。

3 结语

本文基于多元非线性数学模型构建碳纤维纸拉伸强度预测模型，并进行应用分析，检验模型的预测精度。经过应用检测，模型预测准确性较高，其预测值与实际相比绝对误差小于1 kN·m-1，证明所提方法预测值较为准确，具有广泛的应用前景。虽然本文有效提升了预测精度，但仍存在一定不足，未来将继续提升其预测精度。