一致收敛函数列及函数项级数的反常积分性质

费时龙，任雅柔

（宿州学院，安徽 宿州 234000）

0 引言

常见的数学分析教材中讨论了函数列一致收敛的极限函数的连续性、可微性与可积性，获得了极限与积分、求导交换次序的充分条件，并在此基础上研究了函数项级数和函数的连续性、可微性与可积性，获得了求和与极限、导数、积分交换次序的充分条件，但对一致收敛的函数列与一致收敛的函数项级数的反常积分却未见涉及。本文将在一致收敛的函数列极限函数的可积性与一致收敛的函数项级数和函数可积性的基础上，分别讨论它们的反常积分性质与敛散性。

1 一致收敛的函数列极限函数反常积分性质

引理1.1［1］设函数列f n(x)在[a,b]上一致收敛于函数f(x)，且对任意n,f n(x)在区间[a,b]上可积，则f(x)在区间[a,b]上可积,且

注：引理1.1给出了定积分与极限号交换次序的条件,下面定理1.2研究无穷积分与极限号交换次序的条件,定理1.4研究一致收敛的函数列极限函数瑕积分的敛散性并讨论瑕积分与极限号交换次序的条件。

定理1.2 设函数列f n(x)在[a,+∞)上一致收敛于函数f(x)，且满足下列条件:

（1）对任意n,f n(x)在任何有限区间[a,u]上可积；

（3）对任意ε>0,∃M>a,使得对任意n,有

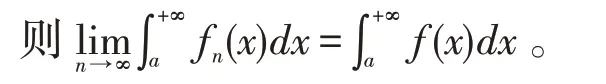
证明由条件（2）及（3）知对任意ε>0,∃M>a,使得对任意n,有

2 一致收敛的函数项级数和函数的反常积分性质

注：引理2.1给出了无穷求和与定积分交换次序的条件,下面定理2.3与定理2.4分别研究无穷求和与无穷积分交换次序以及无穷求和与瑕积分交换次序的充分条件。

3 结语

常见的教材在一致收敛的基础上讨论了定积分与极限号交换次序及定积分与求和号（无穷求和）交换次序的条件，本研究在此基础上分别获得了反常积分与极限号交换次序及反常积分与求和号（无穷求和）交换次序的条件。本文的研究结论丰富了函数列及函数项级数在积分学中的应用范围，后续工作中，还可以进一步研究极限号、求和号与其他积分（如曲线积分、曲面积分等）交换次序的条件。