地震作用下黄土边坡动态滑动位移研究

2022-10-11尹小军王兰民

地震工程学报 2022年5期

尹小军,王兰民

(1.嘉应学院土木工程学院,广东梅州 514015;2.中国地震局兰州地震研究所,甘肃兰州 730000)

0 引言

2008年5月12日14时28分在四川省发生了汶川MS8.0强烈地震。强烈的汶川地震造成了在大约48 678 km2的区域内,诱发了不低于48 000处滑坡[1],其中面积超过50 000m2的大型滑坡多达112处,北川以西王家岩滑坡在瞬间将约1 600人埋入地下[2-3]。地震诱发的坡体变形通常会依次出现三个阶段:第一阶段,共震阶段,即在地震过程中出现一个持时相对较短的地震力和重力共同作用导致的边坡失稳,形成一个垮落面或者沿已有裂隙产生一个永久性位移;第二阶段,即震后阶段,如果震动产生的沿滑移面土体湿剪切强度小于所需维持边坡静态平衡力,则位移持续增加;第三阶段,由于蠕变、固结过程中振动、地表和地下水充填了深部张裂隙,而造成的静水压力降低,位移进一步增加。该研究主要分析地震作用下边坡滑动位移情况。

滑动块体法最早由Newmark于1965年提出[4]。之后,科研人员[4-6]利用纽马克块体法,分析了大量地震作用下边坡滑移问题。Stamatopoulos.C,Ambraseys和Sarma等[7-12]提出了两个块体及多个块体滑坡模型,认为对于较小的滑动位移,单块体模型较合理,但对于非常大的滑动位移,单块体模型是保守的。多块体法能够分析更加复杂的地震边坡问题,通过对临界加速度积分可得共震位移。Rathje,Yeznabad等[13-14]研究了地震作用下滑动位移的估算。朱守彪等[15]根据汶川地震中主要滑坡体的几何及运动特征,研究了地震滑坡的动力学机制。陈春舒等[16]基于极限分析原理,研究了实时动态的Newmark滑块位移法计算,结果比不考虑动态时要小。尹小军[17]研究了地震作用下、降雨与地震耦合作用下黄土边坡的稳定性。

前述研究的模型主要是四边形或三角形滑动块体,而在地震滑坡中,滑动轨迹并非总是沿着直线滑移。大量现场观察表明,多数土体滑坡是沿曲线轨迹滑移,且在滑坡过程中滑动块体的几何形状和土体剪切强度是变化的。据此,笔者提出一个在地震作用下新的边坡滑动模型,该模型由两个滑动块体组成,边坡上部为四边形滑动块体,边坡下部为沿弧线滑移的扇形块体。主要研究两个方面的内容:(1) 求解模型的临界地震加速度系数(kc),计算在三种实例下的临界地震加速度值;(2) 分析推导模型上部块体的滑动位移表达式[u(t)],计算在三种实例下该块体的滑动位移,分析了滑动块体的长度、厚度、交界面倾角对于滑动位移的影响。

1 黄土边坡滑动机理

1.1 前人提出[4,7-8]的模型分析

图1中模型(a)、(c)、(d),滑移面为平面(即直线型滑移线),模型(b)为单个弧面滑动块体。然而,在实际地震黄土滑坡中,大部分边坡滑移面,既有平面,又有弧面,是多种滑移面的组合。

图1 单块体模型Fig.1 Single block model

1.2 问题的定义

本文提出的模型是一个折线边坡,如图2所示,上部边坡的倾角α1、下部边坡的倾角α2、两块体的交面线BNG、其交面线的倾角为β(以G为圆点,顺时针旋转取负,逆时针旋转取正值),取BN的长度为h0。上部边坡滑动体为一个刚性块体,块体为AMNB、边坡的坡长为L、下部边坡滑动体为一个扇形体、半径为R(ON=OC=R)、扇形的圆心角为θ1,OA与OB的夹角为θ0。假设土体为理想刚塑性体,则在滑动的过程中体积不变,滑动块体之间不分离。

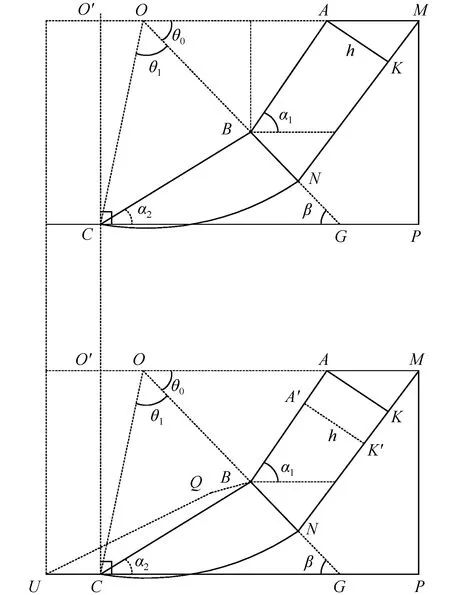
图2 黄土边坡滑动模型Fig.2 Sliding model of loess slope

1.2 基本假设

根据不可压缩性条件,在t时刻块体1沿MN下滑流经BN的土体体积与块体2沿曲线NC下滑流经BC的土体体积相等,即ΔVAA′K′K=ΔVBCUQ可得下式:

(1)

式中：u1为滑动块体1的位移;u2为滑动块体2的位移,λ为两滑动块体位移的比值。

1.3 黄土边坡滑动块体力学分析

边坡两块体受力分析示意图如图3所示。

图3 滑动块体受力分析Fig.3 Mechanical analysis of sliding block

其中：KN和BN线上受剪切力,垂直于BN线上受到的作用力P(t),滑动块体的重力W1和水平方向的地震力k(t)·m1g(图3)。

2 临界地震加速度系数的求解

2.1 黄土边坡滑动块体的平衡方程

根据牛顿第二定律,上部边坡滑动块体AMNB的加速度为:

m1u″1(t)=W1sinα1-Cu[L-u1(t)]-

p(t)cos(90-β-α1)+Cu·h[tan(β-α1)]-1+k(t)·m1gcosα1

(3)

下部边坡块体BNC沿一个圆弧线滑动,设圆心为O,则根据力矩平衡方程可得:

m2ω′l2=W2l2+p(t)(T-h0/2)-ηCu·

Rl0+k(t)·m2gl1

(4)

式中:l0是滑动块体滑移弧长;l1是滑动块体的重力力臂;l2是滑动块体的地震力力臂;l是下部边坡块体BNC的滑动力臂;η是滑动块体剪切强度的折减系数;P(t)是滑动块体间的作用力。

根据式(3)和式(4),可解得P(t) 如下:

(5)

式中:Ms为地震力矩;MG为重力力矩;γ为土体容重;Cu为湿剪切强度。

直接求取扇形滑动体BNC的力臂l是非常困难的,因此,采用间接求解,即利用ONC的力矩减去ONB的力矩,其中,ONC的重力力矩可用微元积分求取。

将式(5)带入式(3)可得下式:

从而解得滑动块体1的表达式:

(6)

2.2 黄土边坡滑动块体的平衡方程

变换式(6)可解得临界地震加速度系数时程:

(7)

式中:kc为临界地震加速度系数时程。由于R-h0/2=R-h/2(α1+β)=X,m1=γh{1/2[2L-hcotα1+hcot(α1+β)]-u1(t)}。

由于重力和地震力为主动力,块体开始滑动,在开始的瞬间,即t=0时刻,u′(0)=u(0)=0,所以,m1可以写成:当u1(t)=0,m1=m10,则m10=1/2γh(2L-hcotα1+hcot(α1+β)),m11=γh·u1(t),其中:m10是滑动块体1滑动前的质量;m11是滑动块体1在t时刻的变化质量。

3 黄土边坡滑动位移

3.1 黄土边坡滑动位移动分析

根据方程式(6),带入m1和m2,

(8)

式中：m20是滑动块体2滑动前的质量,等同于m2。

从而可得下式:

{[(m10+m20·l·sin(β+α2)+u1(t)[γh·X-1l·

sin(β+α2)-γh]}·u″1(t)=u1(t)[Cu+

γh·gsinα1+k(t)·γh·gcosα1]+

m10gsinα1-CuL+Cuh·tan-1(β+α1)-

X-1(η·Cu·Y-MG)sin(β+α1)+

k(t)[m10gcosα1+X-1Mssin(β+α1)]

(9)

化简方程式(9),令式中:A=m10+m20X-1l·sin(β+α2);B=γh[X-1l·sin(β+α2)-1];C=Cu+γh[gsinα1+k(t)·gcosα1]。从而方程式(9)可变为下式:

(10)

3.2 黄土边坡滑动位移计算

式(10)为一微分方程,其求解有三种形式:第一种形式是B=C=0,可简化为最简单的形式;第二种形式是B=0,式(10)可变为二阶微分方程,该方程有两个不相等的实根,从而式(10)可得出通解;第三种形式B=C≠0,此时,该方程很难解得一个实数解。

利用Matlab软件,进行编程,分析优化各参数,可得到式(10)的一个解析解。

3.3 黄土边坡计算参数

通过实验,测得该黄土土样的剪切强度、土体容重值。大量滑坡观测数据表明,在地震作用下,大部分黄土边坡失稳,其边坡倾角位于30°～40°之间。通过室内实验,测得黄土的剪切强度和容重。

4 计算结果

4.1 黄土边坡算例

地震型黄土滑坡按照滑动面深度,可分为浅层滑坡(6 m)、中层滑坡(6～20 m)和厚层滑坡(20～50 m)[18]。

“5·12”汶川地震引起甘肃陇南三家地村大规模黄土滑坡,造成了重大人员伤亡。经中国地震局测定,滑坡区地震烈度为八度,设计地震基本加速度为0.2g,地震动反映谱特征周期为0.4 s。此次地震造成多处滑坡,滑体长度和厚度变化较大,为了便于分析比较,取下列三种典型的滑坡进行计算。

实例1:某滑坡的滑体长度约为160 m,滑坡的前缘宽度约为60 m,滑坡的后缘宽度约为50 m,滑坡厚度约为5 m。

实例2:某滑坡的滑体长度约为350 m,滑坡的前缘宽度约为120 m,滑坡的后缘宽度约为110 m,滑坡厚度约为11 m。

实例3:某滑坡的滑体长度约为710 m,滑坡的前缘宽度约为200 m,滑坡的后缘宽度约为180 m,滑坡厚度约为25 m。

为了便于计算比较,实例各参数如表1所列。

表1 三种实例的物理参数Table 1 Physical parameters of three cases

4.2 临界地震加速度系数的分析

临界地震加速度系数(kc),其取值范围为-1≤kc≤1,当地震加速度系数大于临界地震加速度系数时,边坡失稳,即块体开始滑动。在黄土变化破坏滑移后,在实际块体滑动过程中,土体剪切强度值不是恒定的,而是衰减的,考虑剪切强度衰减时临界地震加速度系数的变化规律。

图4(a)、4(b)和4(c)为β=40°和60°时,实例1、2和3 随土体抗剪强度变化时,地震临界加速度系数的变化规律。

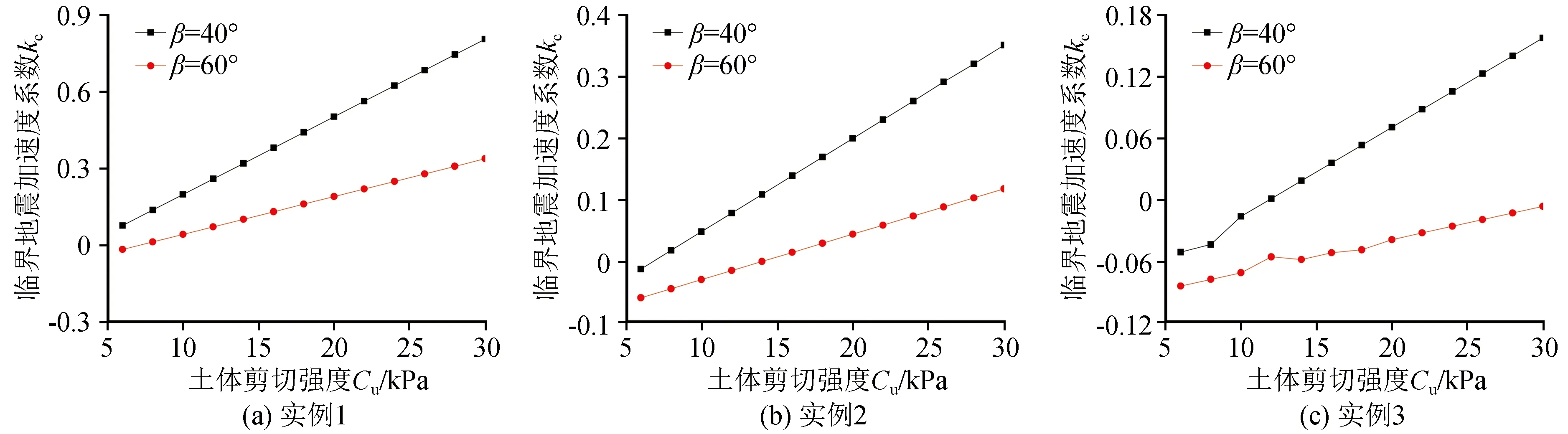
图4 Cu与Kc的变化关系Fig.4 Relationship between Cu and Kc

图5(a)和图5(b)分别给出了β>0和β<0、η=1时,即块体交界面倾角变化时,实例1、2和3滑动块体土体剪切强度变化时,临界地震加速度系数变化的比较。

图5 两块体交界面倾角与临界地震加速度系数的关系Fig.5 Relationship between β and Kc

4.3 黄土边坡滑动位移结果

图6给出了三种不同边坡在两块体交界面倾角为β=40°,k(t)=0.35,土体剪切强度从第1 s时的28 kPa衰减至第5 s的20 kPa时滑动块体的位移变化。

图6 块体位移随时间的变化关系Fig.6 Relationship between block displacement and time

图7给出了三种不同边坡在k(t)=0.4,t=5 s,Cu=20 kPa时块体夹角对滑动位移的影响。

图7 块体交界面倾角与位移的变化关系Fig.7 Relationship between inclination angle of the block interface and displacement

图8给出了滑移块体交界面倾角为40°,黄土边坡上部和下部滑体的倾角均为35° 时,块体滑动位移随土体剪切强度变化的关系。

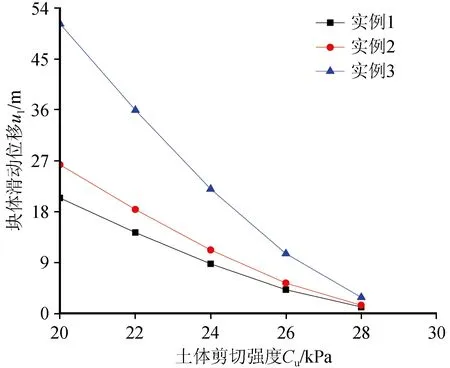
图8 块体滑动位移与土体剪切强度的变化关系Fig.8 Relationship between block sliding displacement and soil shear strength between displacement and shear strength

5 讨论

该研究中,选取的三种实例为地震作用下黄土滑坡的三种不同类型,为了便于分析比较,对选取的物理参数进行适当的优化,选择更为临界的情况进行分析比较。

从图4可知,随着Cu的增加,kc逐渐增大,β=40°时的kc大于β=60°时的kc;且随着Cu的增加,kc的变化量也逐渐增大,实例3的变化量最小,实例1的变化量最大;Cu=6 kPa时,实例3的Δkc=0.033 1,实例1的Δkc=0.093 6;Cu=30 MPa时,实例3的Δkc=0.164 7,实例1的Δkc=0.467 4。

从图5可知,β=40°～80°时,kc逐渐减小,由开始时的迅速减小到后来的缓慢减小,实例1的变化范围最大,为Δkc=0.647 7 ,实例3的变化范围最小,为Δkc=0.214 2;β=40°时,实例1和实例3变化量为Δkc=0.648 6;β=80°时,实例1和实例3变化量为Δkc=0.209 2。

β=-40°～-80°时,kc逐渐较小,且在整个范围内,kc均小于0;实例3的kc变化很小,为Δkc=0.032 5,实例1的kc变化较大,为Δkc=1.257 4;β=-80°时,实例1和实例3变化量为Δkc=0.327 4;β=-40°时,实例1和实例3变化量为Δkc=0.498 3。

当β的大小相同,方向不同时,临界地震加速度系数也不相同,说明块体交界面的倾角方向影响临界加速度系数的大小。

从图6可知,在块体滑动1 s时,三种不同滑块的位移差异很小。当滑移5 s时,实例三的滑块位移是实例二的两倍多,远大于其他两种算例的滑动位移。这表明在相同条件下,滑动块体越大,滑动的位移越大。

从图7可知,在β=40°时,u13是u11的2倍多,u13>u12>u11;随β的增大,u13迅速减少,而u12则逐渐减小,至β=80°时,u降至最小,u12和u11的差异变得很小;这表明滑动块体交界面的倾角β对滑动位移u影响很大,滑块越大,β对u的影响越大。

从图8可知,土体剪切强度Cu对滑块的位移u有很大的影响。在Cu=20时,u13>u12>u11,且Δu较大;当Cu=28时,Δu非常小。这表明,Cu对u的影响非常大,块体越大,u的变化越显著。