地裂缝场地建筑结构动力响应特征及抗震设防研究

杨兴凯,邓亚虹,2,常 江,慕焕东,曹 歌,牛得鑫

(1.长安大学地质工程与测绘学院,陕西 西安 710054;2.自然资源部矿山地质灾害成灾机理与防控重点实验室,陕西 西安 710054;3.西安理工大学岩土工程研究所,陕西 西安 710048)

0 引言

地裂缝是一种典型缓变型地质灾害,广泛分布于我国的汾渭盆地、华北平原以及苏锡常地区,其中又以西安地裂缝发育最为典型、致灾最为严重。地裂缝的存在对城市道路、桥梁、地下管道及建筑结构都造成了不同程度的破坏,其中又以地表建筑破坏尤为显著[1-2]。

至今,关于地裂缝的成因机理,国内外已基本形成共识。自1929年Leonard提出构造成因说以来,先后已有多位国外学者对世界各地的地裂缝成因进行研究,逐渐形成构造与地下水开采复合成因观点[3-6],这一结论与国内学者的研究结论基本一致。目前,国内有关地裂缝成因、分布规律和活动特征等已有较为成熟的研究和认识[7-12],而与工程实践密切相关的研究却相对较少。西安处于构造活动强烈的汾渭盆地,地震灾害威胁严重,因而建筑结构的抗震设防是工程建设中的重中之重。

结构的动力响应与场地的动力特性密切相关,而地裂缝的存在会改变场地固有的振动特性。慕焕东等[13]通过振动台模型实验进行了地裂缝场地地震响应分析,得出了地震放大效应的影响规律与影响范围。范文等[14]通过数值模拟研究了地震作用下地裂缝场地的动力响应,确定了地震动放大效应显著范围,给出了上盘60 m,下盘30 m的避让距离建议;刘妮娜等[15]通过振动台模型试验,发现地震荷载会加速地裂缝上盘的沉降与次级裂缝的生成。张磊刚等[16]、Chang Jiang等[17]、Xuan You等[18]采用地脉动原位测试的方法,研究了地裂缝场地动力响应规律。测试结果表明,地裂缝附近场地的地脉动响应具有明显的放大效应。然而,由于缺乏地裂缝场地地震放大效应的实际监测数据和震害统计资料,《西安地裂缝场地勘察与工程设计规程(DBJ61-6-2006)》规定地裂缝场地上的抗震设防烈度不予提高,建筑物的抗震设计仍按照《建筑抗震设计规范》[19-20]执行,这使得那些位于地裂缝附近,处于地震放大效应影响范围内的建筑可能面临安全隐患。若要对地裂缝场地建筑结构进行合理的抗震设防,须系统的研究地裂缝场地地震放大效应对结构的影响,目前这方面的研究很少,尚处于初步探索阶段。

为此,本文以西安地裂缝场地为研究背景,通过对结构在地震荷载作用下的峰值加速度、层间位移的定量分析与比较,揭示了地裂缝对建筑结构动力响应的影响规律,以及不同基础形式结构之间的动力响应差异,可为近地裂缝场地建筑物的抗震设计与工程建设提供参考。

1 数值分析模型

1.1 模型建立

图1 地裂缝场地各土层分布图(单位:m)Fig.1 Distribution of soil layers in ground fissure site (Unit:m)

表1 土层物理力学参数Table 1 Physical and mechanical properties of soils

上部结构为5层两跨混凝土框架结构,框架层高均为3 m,跨度6 m,柱截面(宽×高)为(0.6×0.6) m2,梁截面(宽×高)为(0.4×0.6) m2,框架梁、柱均采用梁单元模拟。该框架结构的基础分别设置为独立基础、片筏基础、桩基础和桩筏基础。其中独立基础建模时通过结构与土体节点耦合来实现,桩基础和筏板均采用梁单元模拟,分别为梁单元1和梁单元2。梁单元1桩径D为1 m,桩长为10 m;梁单元2截面尺寸(宽×高)为(1 ×1.2) m2。结构所有构件均采用C30混凝土,弹性本构,密度ρ=2 500 kg/m3,泊松比为0.3,弹性模量E=3.0×104MPa。

考虑到模型边界效应对上部结构的影响,选取有限元模型几何尺寸为300 m×80 m。模型地表设置为自由边界,底部为固定约束,两侧设置为自由场边界,从而达到模拟无限自由场地的效果,避免反射波对动力响应的影响[22]。最终建立的地裂缝场地与框架结构的整体模型如图2所示。

图2 有限元模型Fig.2 Finite element model

1.2 计算工况

地震作用下,竖向地震力比水平向地震力要小,并且结构的竖向抗震性能较好,故在时程分析时仅考虑水平向地震动,地震波沿模型底部垂直入射。输入地震波选取El-Centro波,经过滤波和基线校准后的地震波时程曲线及傅里叶谱如图3所示。根据《建筑抗震设计规范》,将地震波峰值调整为0.1g、0.2g及0.4g,分别代表多遇地震、设防地震和罕遇地震。同时考虑结构距地裂缝距离和结构基础形式对其地震响应的影响。其中结构分别位于场地上盘和下盘距地裂缝3、6、12、18、24及36 m处。具体计算工况如表2所列。

表2 计算工况Table 2 Conditions of the calculation

图3 El-Centro波加速度时程及傅里叶谱Fig.3 Acceleration time-history and Fourier spectrum of El-Centro wave

1.3 模态分析

动力分析之前,先对模型进行特征值分析,分别求出框架结构和土体的自振频率。结构的前两阶自振频率分别为3.76 Hz和12.40 Hz,土层的前10阶自振频率如表3所列。材料阻尼选取Rayleigh阻尼,阻尼矩阵的表达式为[23]:

表3 土体自振频率Table 3 Natural frequencies of soil

[C]=α[M]+β[K]

(1)

式中:[C]为阻尼矩阵;[M]和[K]分别为质量矩阵和刚度矩阵;α和β分别为与质量和刚度相关的阻尼系数,量纲分别为s-1和s。

阻尼系数可根据第i、j阶振型的固有圆频率ωi、ωj和与圆频率对应的阻尼比ξi、ξj计算,其计算公式为:

(2)

式中:ωi=2πfi,ωj=2πfj;fi和fj分别为第i、j振型的自振频率。

由于主要分析结构的水平向振动,故选取水平方向质量参与系数最大的两阶模态对应的自振频率,因此取f1=0.894 6 Hz,f2=1.768 5 Hz,土体阻尼比取ξ1=ξ2=0.1,计算得到土体阻尼系数α=0.746 6 s-1、β=0.011 2 s。选取上部结构前两阶自振频率来计算其阻尼系数,取f1=3.76 Hz、f2=12.40 Hz,混凝土阻尼比取ξ1=ξ2=0.05,计算得到结构阻尼系数α=1.812 8 s-1、β=0.001 0 s。

2 场地地表加速度响应分析

在进行结构动力分析之前,先进行无结构地裂缝场地的动力响应分析。分别在上、下盘距地裂缝0、3,6、12、18、24、30、36、48及60 m处布置测点。测点布设如图4所示。

图4 地裂缝场地地表测点布设图Fig.4 Layout of surface monitoring points in ground fissure site

图5为场地地表峰值加速度的变化曲线。由图可知,随着输入地震波峰值加速度的增大,地表峰值加速度也增大。越靠近地裂缝,峰值加速度越大,并且随着距地裂缝距离的增大逐渐减小,上、下盘均在24 m以后趋于稳定,表明地裂缝放大效应的影响范围约为24 m。这与文献[13]得到的地表加速度变化规律相符,同时也说明模型的边界效应不明显,模拟效果良好。

图5 地裂缝场地地表峰值加速度Fig.5 Peak ground accelerations in ground fissure site

定义地表峰值加速度放大因子为测点峰值与平稳峰值的比值。其中平稳峰值取上、下盘距地裂缝最远处3个测点的平均值。取距地裂缝3 m处的测点为分析对象,计算其峰值加速度放大因子(表4)。由表可知,输入地震波峰值加速度为0.2g时加速度放大因子最大,0.1g的放大因子次之,0.4g的最小;同时,上盘峰值加速度明显大于下盘,即存在“上盘效应”。

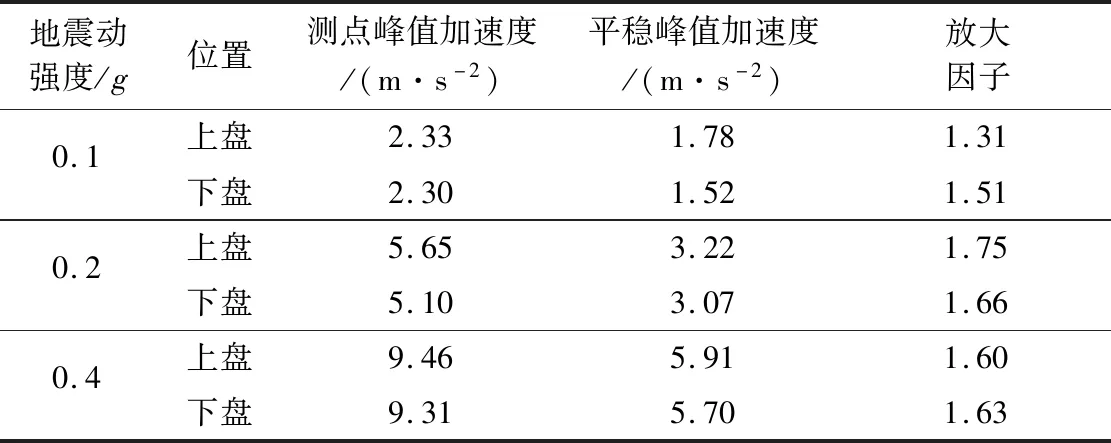
表4 地表峰值加速度及放大因子Table 4 Peak ground accelerations and amplification factors

3 结构动力响应特征分析

3.1 结构加速度响应分析

考虑篇幅,仅以距地裂缝3 m的桩筏基础结构为分析对象进行说明。由于结构加速度峰值出现的时刻与输入波加速度峰值出现的时刻接近,均在前10 s内,故仅截取前10 s的结构加速度时程曲线。图6为结构在0.2gEl-Centro波作用下各层加速度的时程曲线。整体来看,结构无论是位于地裂缝上盘还是下盘,其加速度的响应规律相似;各层加速度响应除大小有差异外,其时程变化规律基本一致。但是结构顶层加速度峰值出现的时间并不完全相同,上盘出现在2.60 s,下盘出现在2.63 s,两者存在0.03 s的时间差。这是因为地震波经过地裂缝时发生复杂的反射和折射,其传播方向和能量发生变化[18],使得上、下盘结构基础附近的地震波产生明显差异,即结构受到非一致性激励,故其加速度的峰值时间存在一定差异。

图7为结构峰值加速度随层高的变化曲线。由图可知,结构峰值加速度随层高的增大而增大,顶层峰值加速度最大,同时上盘各层峰值加速度略大于下盘,即上盘效应,且层数越高,两者差值越大。上、下盘结构峰值加速度变化规律相似,整体均呈现“S”形,可将其大致分为三部分：1～2层,2～4层,4～5层。其中中间2～4层峰值加速度变化幅度最大,而底层和顶层的变化幅度相对较小。

定义楼层峰值加速度与输入地震波峰值加速度之比为结构楼层的加速度放大系数(下同),如表5所列。由表可知,加速度放大系数与层高无明显线性关系,其随着层高的增大而增大,顶层放大系数最大,最大可达4.24倍。对比上下盘放大系数可得,各层放大系数上盘均大于下盘。

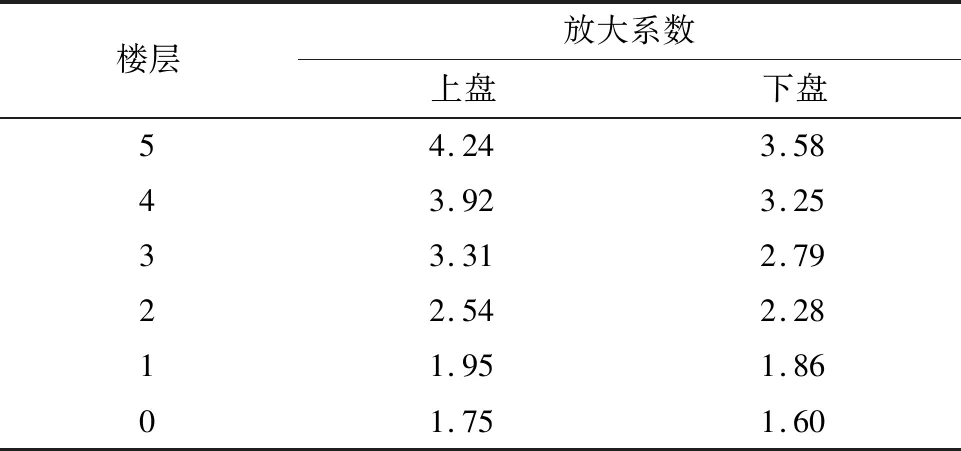
表5 结构加速度放大系数Table 5 Peak acceleration amplification factors of structure

3.2 结构位移响应分析

图8为结构在0.2gEl-Centro波作用下各层侧向位移的时程曲线。由图可知,位于地裂缝上、下盘的结构,其侧向位移时程变化规律相似,各层侧向位移变化基本一致,这表明在振动过程中,结构主要发生一阶水平向振动。在同一时刻,上、下盘结构侧向位移值存在一定差异,峰值时间也略有不同。上盘在2.27 s达到峰值,下盘在2.31 s达到峰值,这主要是由地裂缝场地的特殊动力特性所引起的。

图8 结构侧向位移时程曲线Fig.8 Lateral displacement time-history curves of structure

图9为结构层间位移角随层高的变化曲线。由图可知,无论结构位于地裂缝上盘还是下盘,其层间位移角均随层高的增大先增大后减小,最大层间位移角均出现在第二层;同时,结构层间位移角也表现出明显的上盘效应,这说明上盘结构遭受的地震作用更加强烈,在进行地裂缝场地的结构抗震设计时还需区别对待上、下盘,比较而言,上盘需要更高的设防水平。

图9 结构各层层间位移角Fig.9 The story drift ratio of each layer of structure

4 结构动力响应影响因素分析

4.1 地震动强度对结构动力响应的影响分析

图10为不同地震动强度作用下,结构峰值加速度随层高的变化曲线。由图可知,随着输入地震动强度的增大,各楼层加速度也增大。对比上、下盘结构的加速度可知,上盘效应在结构顶层表现得最为明显,而结构底层的加速度没有明显差异;并且随着地震动强度的增大,上下盘结构之间的加速度响应差异进一步扩大。

图10 结构峰值加速度随层高变化曲线Fig.10 Change curve of structural peak acceleration with story height

图11为结构加速度放大系数最大值随输入地震动强度的变化曲线。由图可知,上盘加速度放大系数最大值大于下盘,并且随着输入地震动强度的增大,最大放大系数反而有所减小。这主要是因为随着地震动强度的增大,土体非线性增强,并逐渐进入塑性状态,导致土体传递振动能量的能力不断减弱。

图11 加速度放大系数最大值随输入地震动强度 变化曲线Fig.11 Change curve of maximum acceleration amplification factor with the input ground motion intensity

图12为结构层间位移角随层高的变化曲线。由图可知,层间位移角随着输入地震波峰值加速度的增大而增大,并且上盘结构层间位移角明显大于下盘,即上盘效应。与结构加速度不同的是,结构各楼层的层间位移角均表现出明显的上盘效应,并且随着地震动强度的增大,上盘效应越显著。

图12 结构层间位移角随层高变化曲线Fig.12 Change curve of structural story drift ratio with story height

4.2 基础形式对结构动力响应的影响分析

图13为0.2g地震波作用下不同基础形式的结构峰值加速度随层高的变化曲线。由图可知,无论何种基础形式,上盘和下盘结构的加速度响应均明显不同。同时,无论结构位于地裂缝的上盘还是下盘,片筏基础、桩基础和桩筏基础结构的加速度响应接近,而独立基础结构的加速度响应与前三者差异明显。整体而言,独立基础各层差异较其他三种基础要小,表现为底层略小而高层略大。表6给出了结构各层加速度放大系数,取结构顶层的放大系数进行分析。当结构位于地裂缝上盘时,桩基础放大系数最大,片筏基础、桩筏基础次之,独立基础最小;当结构位于地裂缝下盘时,片筏基础放大系数最大,桩筏基础、桩基础次之,独立基础最小。

图13 不同基础形式结构峰值加速度Fig.13 The peak acceleration of structure with different foundation forms

表6 不同基础形式结构加速度放大系数Table 6 Acceleration amplification factors of structure with different foundation forms

图14为层间位移角随层高的变化曲线。由图可知,不同基础形式的结构,其层间位移角随层高的变化规律相似,但最大层间位移层有所不同。独立基础结构的最大层间位移层为第三层,其余基础形式的结构均为第二层。除此之外,基础形式对结构层间位移响应的影响随层高略有差异,结构底层的层间位移角差异较为明显,随着楼层的增大,基础形式对结构层间位移角的影响逐渐减弱。

图14 不同基础形式结构层间位移角Fig.14 The story drift ratio of structure with different foundation forms

综上可知,不同基础形式的结构,其动力响应存在差异。这是因为结构的基础形式不同,场地土-结构相互作用机理不同,同时叠加地裂缝对结构的影响,在二者的共同作用下所造成的。故在结构抗震设计时,应考虑到基础形式对结构的动力响应的影响。

4.3 结构距地裂缝距离对其动力响应的影响分析

图15为结构顶层峰值加速度及最大层间位移随距地裂缝距离的变化曲线。由图可知,在地裂缝附近区域,结构峰值加速度和最大层间位移均具有明显的放大效应。越靠近地裂缝,结构响应峰值越大,随着距地裂缝距离的增大,峰值逐渐减小,并且对称位置处的结构上盘响应峰值大于下盘。综合考虑峰值加速度和最大层间位移的变化规律,当结构与地裂缝距离大于24 m时曲线趋于平稳,结构响应基本一致,表明地裂缝的放大效应影响范围约为24 m,该距离可作为建筑物的安全避让距离。同时,在该范围以内的建筑物面临较大地震破坏风险,须提高其抗震设防水平。

图15 结构顶层峰值加速度及最大层间位移随距离的变化曲线Fig.15 Change curves of peak acceleration at the top story and maximum inter-layer displacement of structure with distance

由上分析可知,在距地裂缝较远区域(大于24 m),结构响应峰值基本一致,故取其均值作为不受地裂缝放大效应影响的“平稳峰值”,同时定义放大因子为:结构响应峰值与平稳峰值的比值。图16为结构顶层峰值加速度和最大层间位移放大因子随距离的变化曲线。从图中可以看出,放大因子随距离的变化规律同峰值的变化规律相似,上、下盘放大因子均在距地裂缝3 m处最大,且随距离的增大逐渐减小并趋于稳定。其中,峰值加速度最大放大系数上盘为1.27,下盘为1.28;最大层间位移的最大放大系数上盘为1.35,下盘为1.22。

图16 放大因子随距离变化曲线Fig.16 Change curves of amplification factors with distance

5 结论

本文以西安地裂缝场地为研究背景,研究了地裂缝场地上的框架结构的峰值加速度、层间位移等动力响应特征,并分析了其影响因素和影响规律,得出如下结论:

(1) 地裂缝附近场地上的结构加速度响应和层间位移响应具有明显的放大效应。动力响应峰值随着距地裂缝距离的增大逐渐减小,最终趋于稳定,放大效应的影响范围为24 m左右,此范围以内的结构面临较大地震破坏风险,需提高其抗震设防水平。

(2) 结构的峰值加速度随层高的增大而增大,整体呈现出“S”形,层间位移角随层高的增大先增大后减小。二者均表现出明显的“上盘效应”,即上盘结构响应强于下盘,且随着地震动强度的增大,上下盘结构动力响应差异进一步扩大,上盘效应愈发显著。

(3) 片筏基础、桩基础和桩筏基础结构的加速度响应接近,而独立基础结构的加速度与前三者差异明显,但随着楼层的增大,基础形式对结构层间位移角的影响逐渐减弱。

(4) 上、下盘结构的峰值加速度、峰值位移大小及峰值出现的时间等存在一定差异,这是由于地震波经过地裂缝时发生复杂的反射和折射,结构受到非一致性激励造成的。