三角域上的3阶P-Bézier曲面

熊 建

(安徽审计职业学院 综合教育学院, 安徽 合肥 230601)

曲面造型技术是计算机辅助设计、计算机辅助制造和计算机图形学的核心技术之一,曲面造型的一个最基本问题是对曲面的设计和表示[1-3]。作为应用较为广泛的Bézier曲面,主要包括矩形域上的张量积曲面和三角域上的非张量积形式的三角曲面[4-5]。三角域上的曲面造型设计,更有利于解决构型复杂、形状和边界不规则的几何造型问题,已成为计算机辅助设计、计算机辅助制造和计算机图形学中造型技术研究的热点。

现有文献中,对传统多项式空间中的Bézier三角曲面进行了较广泛的研究[6-7]。但多项式空间中的Bernsten-Bézier基的非有理形式造型能力有限[8-10],而有理形式又因其复杂性[11],从而具有分母零点的奇异值、权因子调节困难、求导求微分的次数升高等缺陷[12-14]。人们尝试寻找非多项式空间中的Bézier型基[15-17]。而如何把这些非多项式空间中的Bézier型基推广到三角域上,从而完善这类Bézier型基的三角曲面造型理论，成为曲线曲面的研究方向之一[18-20]。沈莞蔷等[18-19]将三角多项式空间中3阶、5阶P-Bézier基推广到三角域上,魏永娟等[20]将4阶C-Bézier基推广到三角域上,陈素根等[21-22]将3阶、4阶T-Bézier基推广到三角域上。三角域上的n次Bernsten-Bézier基包含了(n+1)(n+2)/2个基函数,3阶Bézier型基都是拟2次的[18,21],推广到三角域上基函数为7个,比三角域上的2次Bernsten-Bézier基函数个数多了1个。

本研究将3阶P-Bézier基进行非张量积形式的二元推广,构造出三角域上含6个函数的3阶P-Bézier基函数组,其与三角域上的2次Bernsten-Bézier基函数组具备相似特性。基于该基函数组定义的3阶P-Bézier三角曲面片,具备2次Bézier三角曲面片相似特性,如角点插值性、凸包性、对称性、几何不变性和仿射不变性等。本研究构造的3阶P-Bézier三角曲面片的控制顶点个数比文献[18]少1个,计算更简便。尤其,当α=π/2时,为文献[22]构造的三角曲面。

1 三角域上3阶P-Bézier基函数

1.1 回顾

文献[9]在三角多项式空间Γ={1,sint,cost}上定义的3阶P-Bézier基函数为:

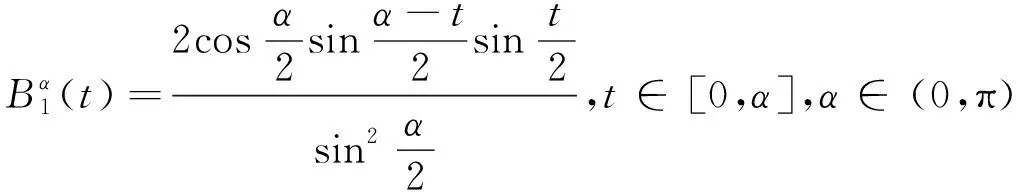
(1)

1.2 三角域上基函数的定义及性质

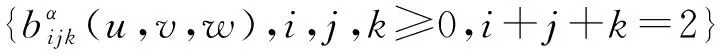
定义1 在D={(u,v,w)|0≤u,v,w≤α,u+v+w=α,α∈(0,π)}上,设

(2)

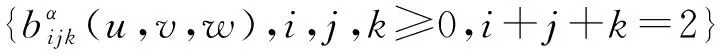
基函数组的性质:

性质4:(端点性质)

证明:由式(2)经计算易证性质1,2,3,4成立,下证性质5成立。

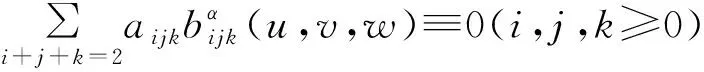
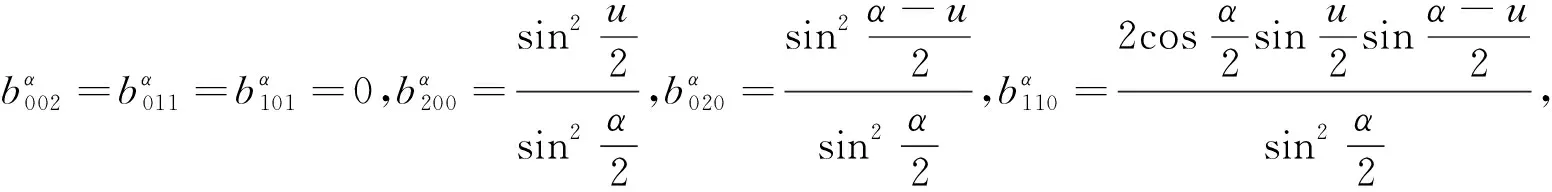
同理,令u=0,w=α-v可证a020=a002=a011=0;令v=0,u=α-w可证a200=a002=a101=0。

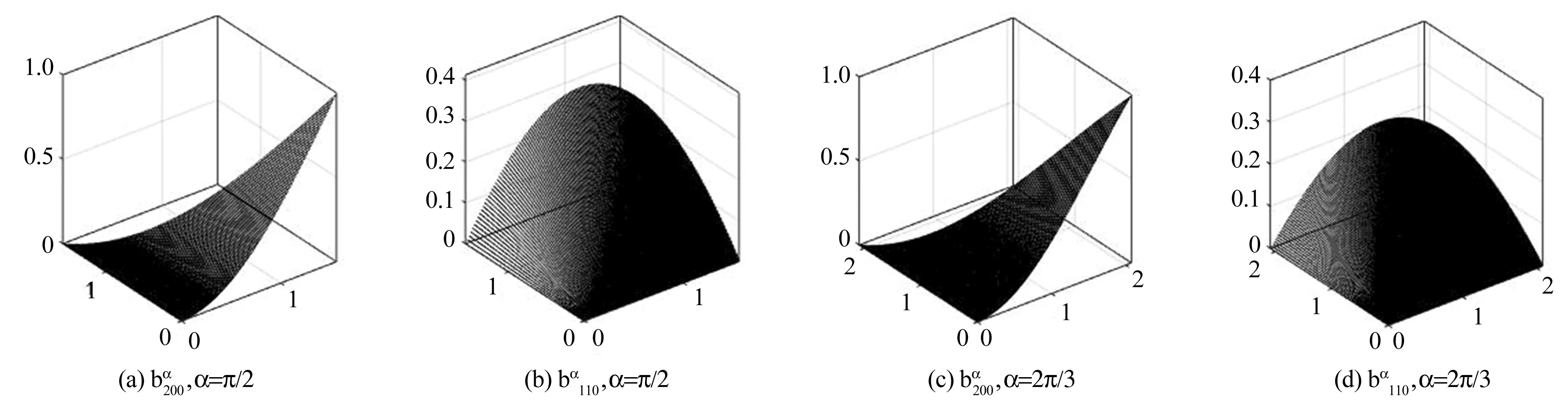
图1 三角域上3阶P-Bézier基函数部分图形Fig.1 Partial graphics of the 3-order P-Bézier basis in triangular polynomial sapce

2 三角域上3阶P-Bézier曲面

定义2:对任意(u,v,w)∈D及给定的控制顶点Pijk,i,j,k≥0,i+j+k=2,称

(3)

此为三角域上3阶P-Bézier三角曲面片。

3阶P-Bézier三角曲面片的性质:

性质6:(凸包性)3阶P-Bézier曲面片位于控制顶点构成的控制网格包围中。

性质7:(几何不变性和仿射不变性)

曲面片S(u,v,w)的几何形状不依赖于坐标系,与控制顶点有关,对控制顶点作仿射变换就是对相应的曲面片S(u,v,w)作同样的仿射变换。

性质8:(对称性)

性质9:(曲面片的边界性质)

(1)边界曲线:3阶P-Bézier三角曲面片的边界曲线是以控制网格的边界作为控制多边形生成的3阶P-Bézier曲线;

(2)角点插值性质:S(α,0,0)=P200,S(0,α,0)=P020,S(0,0,α)=P002;

(3)角点处的切平面:3阶P-Bézier三角曲面片S(u,v,w)在三个角点P200(α,0,0),P020(0,α,0),P002(0,0,α)处的切平面分别由P200P110P101,P020P011P110,P002P101P011所张成。

证明:由基函数组的性质易证性质6～8及性质9之(1),(2),下面证明性质9(3)成立。

令w=α-u-v,过S(u,v,w)上任意点(u,v,α-u-v)处的切平面如下:(其中β,γ∈R)

同理可证(u,v,w)=(0,α,0)与(u,v,w)=(0,0,α)处的情况。

3 应用实例

例1:图2分别给出参数α=0.25π、0.5π、0.75π、0.9π时,三角域上的3阶P-Bézier曲面片的图例,其中控制顶点分别为P200(1,0,0),P110(0.7,0.7,0),P020(0,1,0),P011(0,0.7,0.7),P002(0,0,1),P101(0.7,0,0.7)。

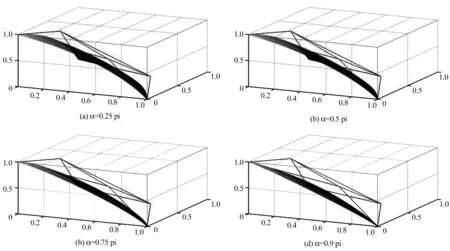
图2 三角域上3阶P-Bézier曲面片Fig.2 The 3-order P-Bézier surface over triangular domain

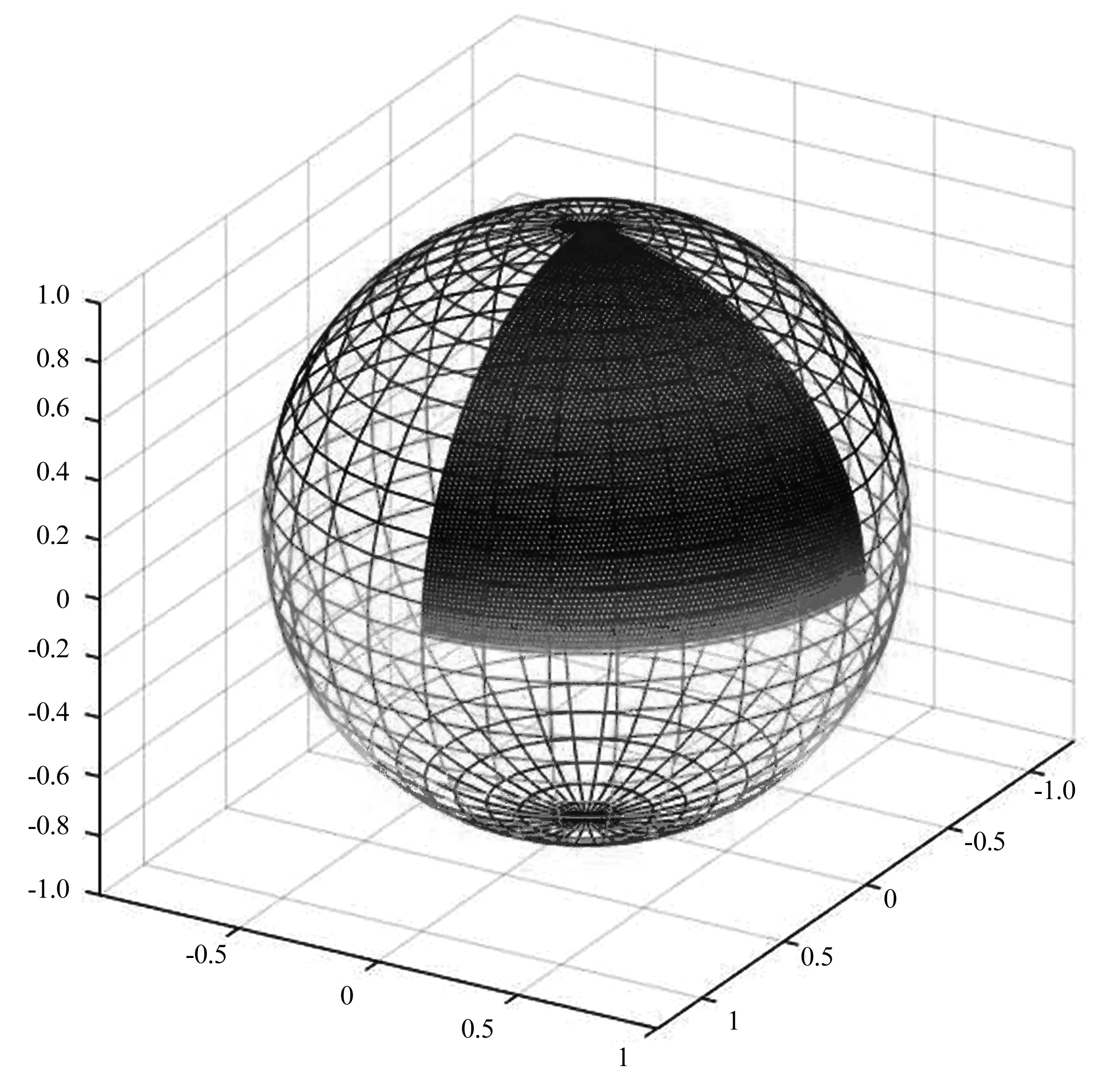
图3 3阶P-Bézier曲面片近似表示1/8单位球面Fig.3 1/8 unit sphere in 3-order P-Bézier

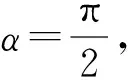
4 结论与展望

本研究将三角多项式空间Γ={1,sint,cost}中的3阶P-Bézier基函数进行非张量积形式的二元推广,提出了由6个三角多项式函数构成的三角域上的基函数组,该基函数组具备3阶Bézier基函数组的类似性质。由这组基生成的三角曲面片与3阶Bézier三角曲面片具备类似特性,例如凸包性质、对称性质、几何不变性质和仿射不变性质及角点插值性质等。该三角曲面片能够近似表示球面片,也能够实现三通管接口处的连续光滑拼接。应用实例表明,运用本文方法构造的三角曲面造型是一种实用有效的曲面设计方法。

3阶P-Bézier三角曲面片是否具有升阶、细分等性质;曲面的拼接条件及保凸性要求等都是后续可以继续研究的课题。