基于人工-真实样本度量学习的指针式仪表检测方法
2022-10-11翟永杰赵振远王乾铭白康
翟永杰,赵振远,王乾铭,白康
(华北电力大学自动化系, 河北 保定 071003)
0 引 言
为了支撑起不断扩大的工业生产规模,实现工业生产的自动化智能化已势在必行[1]。各种测量仪表作为自动化系统的信息输入来源,其数量也急剧增加,如何准确地获取测量仪表的读数成为实现工业自动化的首要问题。目前的测量仪表从显示形式上分为两种,指针式仪表和数字式仪表。对于指针式仪表,一方面因其本身结构简单、可靠性高、反应灵敏、制造成本低等优点被广泛应用在工业生产中[2-3];另一方面,虽然数字化仪表已经成为仪表行业发展的新趋势,但是在很多实际生产环境中,如变电站,由于电磁干扰等环境因素的影响,不宜采用数字式仪表[4-5];第三,因历史遗留原因造成了指针式仪表大规模应用,且无法在短时间内全部进行升级,因此实现对指针式仪表的自动读数就显得尤为重要[6-7]。
指针式仪表没有数据输出接口,其测量结果无法直接被计算机系统采集分析,需要通过人工手动采集并输入计算机系统[8-9]。考虑到在高危生产环境中运维人员不方便进入现场抄表,并且人工读数存在成本高、效率低、结果易引入主观因素等原因[10],利用智能巡检机器人携带摄像头代替人工进入现场,通过计算机视觉技术完成对测量仪表的自动读数是当前主流的方式[11-12]。仪表的自动读数分为两个阶段[13],分别是仪表的检测和仪表的识别,前者从复杂背景中将仪表表盘区域标出,后者在前者的基础上进行仪表读数的判定。仪表识别的准确率严重依赖仪表表盘区域检测的准确性,因此高精度的仪表检测技术成为实现指针式仪表自动读数系统的前提条件。
针对仪表检测方法,国内外的学者进行了大量研究,大致可以分为两类:
一类是基于传统计算机视觉原理的算法。文献[14]利用SIFT(Scale Invariant Feature Transform)算法通过关键点匹配完成指针式仪表检测;文献[15]提出了利用改进的ORB算法实现了指针式仪表的搜索;文献[16]提取待识别图片和模板图片的KAZE特征,并采用KNN(K-Nearest Neighbor)算法完成特征匹配,从而得到了表盘区域。该类算法对噪声太敏感、泛化能力差、复杂度高、容易漏检和误检,不适用工程应用;
另一类是基于深度学习的目标检测算法。随着深度学习的发展,已经有许多学者利用其解决指针式仪表目标检测的问题,且已经取得不错的成效。文献[17]通过SSD目标检测模型对指针式仪表进行检测定位,并取得不错的检测结果;文献[18]提出一种基于Faster R-CNN的指针式仪表识别算法,通过引入Focal loss损失函数和特征金字塔(FPN)来提升检测精度;文献[19]提出一种基于改进预训练MobileNetV2网络模型与圆形Hough变换相结合的方法来提升对圆形指针式仪表的检测精度和速度;文献[20]提出了一种基于YOLOv4和霍夫变换的指针式仪表检测方法,通过对YOLOv4提取出的区域进行霍夫变换精确定位指针式仪表。上述算法都在一定程度上提高了仪表的检测精度,但是由于指针式仪表种类繁多,算法需要大量数据进行训练才能保证神经网络收敛,进而达到有效的检测精度,然而在实际生产环境中采集到足够多的数据往往是不切实际的,因此实际检测精度依然较低。文献[21]提出一种基于深度卷积神经网络与虚拟样本结合的指针式仪表检测方法,利用先验知识构建指针式仪表虚拟样本生成模型,解决深度神经网络面临的小样本难题;文献[22]使用网络爬虫及数据增强技术扩充数据集来解决指针式仪表检测过程中样本不足的问题,并在YOLOv3的基础上结合Kmeans++初始化的Mini Batch Kmeans方法得到改进模型。上述算法通过使用人工虚拟图像或使用爬虫技术爬取指针式仪表的图像对训练集进行扩充,但是这些图像与实际生产环境中的图像有较大的差异,无法通过简单混合训练集使神经网络得到有效的训练,导致在实际生产环境中检测效果差、精度低。
以上研究表明,相对于传统的机器视觉算法,基于深度学习的目标检测算法在进行指针式仪表检测任务时更具优势,但真实场景下的样本数量不足和质量过低问题严重制约着深度学习在本任务中的应用。
针对这一问题,提出了一种基于人工-真实样本度量学习的指针式仪表检测方法,通过深入研究指针式仪表的结构并结合人工抄表的经验,提取出指针式仪表在表盘检测中的显著部分,并对其进行建模;同时将度量学习机制引入目标检测模型中,定义一种相似度量损失函数来驱动神经网络的训练。以上方法可实现在少样本情况下更高的检测精度,为指针式仪表的检测提供了新的思路。
1 设计方案
1.1 算法框架
通过对指针式仪表结构的分析和研究,以及结合度量学习的网络特性,文中算法总体框架如图1所示。

图1 文中算法框架
文中算法以Faster R-CNN目标检测模型为基线模型(Baseline),在其基础上以相似度量损失函数的形式融合度量学习机制。在网络训练时,首先将真实样本与人工基准样本分别输入权值共享的特征提取网络提取特征,然后,一方面利用真实样本生成的特征在真实样本上生成建议框,结合标注信息通过感兴趣区域池化操作将特征缩放到统一大小,并通过预测网络对真实样本中目标的位置和类别进行预测,将预测结果与标注信息进行对比,从而计算位置损失和类别损失。另一方面,将人工基准样本与真实样本中目标区域对应的特征输入特征相似性度量模块,计算相似度量损失。最后,将三种损失按一定比例结合进行统一优化。相似度量分支通过相似度量损失函数间接参与到真实图像的预测网络中,该分支仅在训练时起作用,不降低原模型的预测速度。
1.2 指针式仪表结构分析
一般指针式仪表如图2所示,按结构可以大致划分为四个部分,分别是刻度线、刻度值、指针、表盘背景。

图2 指针式仪表
在指针式仪表图像中,刻度线由多段短线组成,短线的长度一般呈规律变化,间隔均匀或非均匀(非线性指针式仪表)地分布在仪表表盘上,并在特定圆周上做辐射状排布。由于拍摄角度和拍摄设备的内参数导致图像出现不同程度的畸变,使得原来按照圆周排布的刻度线变成按照椭圆排布,刻度线的长度也发生一些微小变化;刻度值与刻度线在仪表表盘上的排列相似,并与刻度线相邻,按照仪表种类的不同可能出现在刻度线的内侧、外侧或者两侧(双刻度指针式仪表),刻度数值一般遵循等差数列或者等比数列(非线性指针式仪表);指针为细长条状,围绕某一定点作回转运动,该定点一般与刻度线围成的圆周圆心重合,其长度比刻度线围成的圆周半径略长并小于直径。上述三种结构都有利于指针式仪表的检测,但是通过分析刻度线、刻度值与指针在表盘区域的像素占比可知,如图3所示,刻度线的像素占比明显高于刻度值与指针的像素占比,因此称刻度线为指针式仪表检测过程中的显著特征,刻度值与指针称为非显著特征。在建模时应优先考虑显著特征,并称通过建模得到的、只包括显著特征信息的图像为人工基准图像或人工基准样本。表盘背景包括仪表名称、仪表单位、生产厂家、适用条件等,这些信息出现位置不定,数量不定,内容不同,无法成为有效的仪表检测特征。
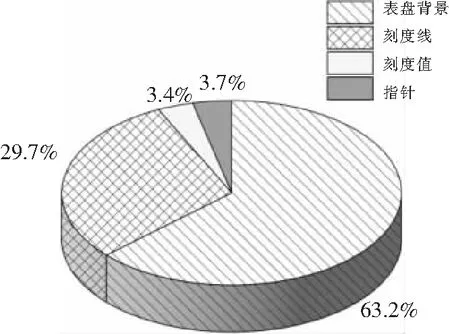
图3 指针式仪表结构占比分析
为使神经网络有充足的数据得到训练,并且优先学到指针式仪表的显著特征,设计了人工基准样本生成算法(Artificial Benchmark Sample Generation Algorithm,ABSGA),该算法流程图如图4所示。
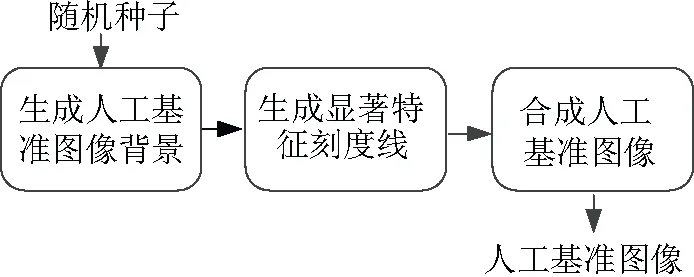
图4 ABSGA 流程图
ABSGA通过输入不同随机种子,随机生成不同的人工基准图像,该算法分为三个部分:
首先生成人工基准图像背景,通过统计分析,真实场景中表盘背景的颜色多为灰(gray)、白(white)、黑(black),因此ABSGA在HSV颜色空间按照表1所示参数,并根据式(1)对表盘背景进行随机颜色初始化。

表1 HSV颜色对照表
(1)

其次按照式(2)随机生成与表盘背景有一定对比度的刻度线特征。
(2)
式中c′表示刻度线颜色。
最后将图像从HSV颜色空间转回RGB颜色空间,并施加式(3)所示的仿射变换。
(3)
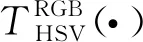
人工基准图像样例如图5所示,相较于其他方式生成的人工图像,ABSGA生成的人工基准图像仅包含指针式仪表的显著特征,可以使得神经网络更加专注显著特征的学习,更有利于引导网络的训练。

图5 人工基准图像样例
1.3 特征相似性度量模块
度量指衡量两个元素之间距离的函数,也叫做距离度量函数。度量学习[23-25]也称为距离度量学习或者相似度学习,指通过给定的或学习到的距离度量函数计算两样本对之间的距离,从而度量样本间相似度。基于度量学习方法的一般流程如图6所示,该框架具有两个模块,分别是嵌入模块F和度量模块S,嵌入模块F通过对样本进行特征提取操作得到特征向量,并将其映射到低维向量空间以减少运算量和降低特征之间的耦合,提高不同特征之间的差异;之后根据度量模块S计算出特征之间的差异,进而计算相似度得分。度量模块S通常采用余弦相似度[26]。
度量学习发展至今已有广泛的研究和应用,文献[27]在2015年提出使用孪生神经网络(Siamese Neural Network)进行图像分类任务,如图7(a)所示。该网络是一种相似性度量模型,通过两个共享权值和参数的卷积神经网络将输入的图像对映射到低维向量空间,使用简单的距离函数进行相似度计算。按照最小化同类样本之间距离、最大化异类样本之间距离的规则定义损失函数,并用其驱动神经网络的训练。
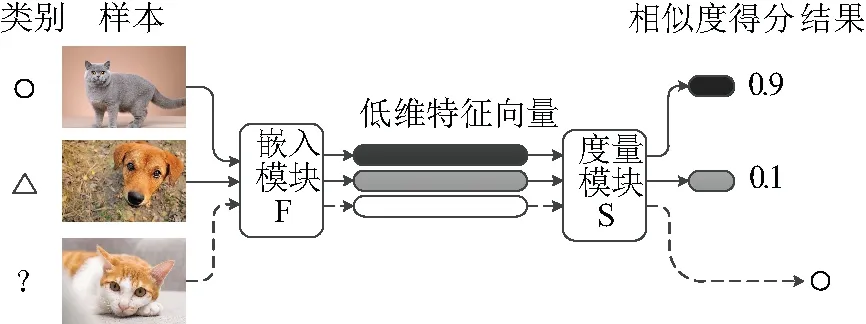
图6 度量学习一般流程图
由孪生神经网络的特性,很自然有如下观点:如图7(b)所示,假设在孪生神经网络的一侧输入人工基准图像,另一侧输入真实图像,由于人工基准图像包括了真实图像的显著特征信息,因此在损失函数的驱动下,两侧图像的特征将逐渐相互靠近,在特征空间中形成点簇,即两侧图像通过该网络提取到的特征会“自然”聚集在一起。一方面该特性可以在特征空间中降低或消除人工图像和真实图像的分布差异,另一方面,由于人工基准图像只包含显著特征信息,由人工基准图像提取到的特征向量会更具有针对性和稀疏性,有利于使特征提取网络学会区分显著特征信息。对目标检测网络来说,通常前置网络是一个特征提取网络,本质上是一个特征嵌入模块F。因此,将度量学习引入目标检测网络,同时把通过建模生成的指针式仪表图像作为人工基准图像,同样会使待检测图像的特征和人工设计图像的特征相互靠近。与孪生网络不同的是,为了适配目标检测任务,实际参与匹配的是输入图像对的一部分。具体来说,待检测图像经过特征提取之后,通过标注的真值框(GT_boxes)提取出指针式仪表表盘区域,取该区域在特征图上的映射作为感兴趣区域(Region of Interest,RoI),由该RoI参与度量模块的计算。同理,输入人工图像的分支也进行相同的操作。
通过对指针式仪表结构的研究和分析,对指针式仪表的显著特征刻度线进行建模,并以此生成人工基准图像输入网络,使得输入的真实图像经过特征提取网络后,在低维特征向量空间内都会与该基准图像的特征彼此靠近。通过引入指针式仪表的显著特征,使得特征提取网络能够“有选择”地学习真实图像中与人工基准图像相似的特征,达到指导神经网络训练的目的。
为了更加充分地阐述特征相似度量模块,以Faster R-CNN为基线模型,详细说明该模块的结构。如图8所示,在Faster R-CNN中引入新的网络分支,该分支的特征提取网络与Faster R-CNN的特征提取网络共享一套权值,用于提取输入图像的特征。之后使用自适应全局平均池化操作,将特征图的尺寸压缩为2 048维的向量。为了进一步对图像特征向量进行精炼简化,通过一个全连接层对特征向量进一步压缩,并使用反余弦函数(Tanh)和纠正线性单元(Rectified Linear Unit,ReLU)作为激活函数进行非线性操作,将全连接层输出的特征值限制在特定的范围内。最终输出更低维度的向量,称为输入图像的特征向量,网络结构如表2所示。通过比较两图像RoI的特征描述向量,完成特征相似性度量。
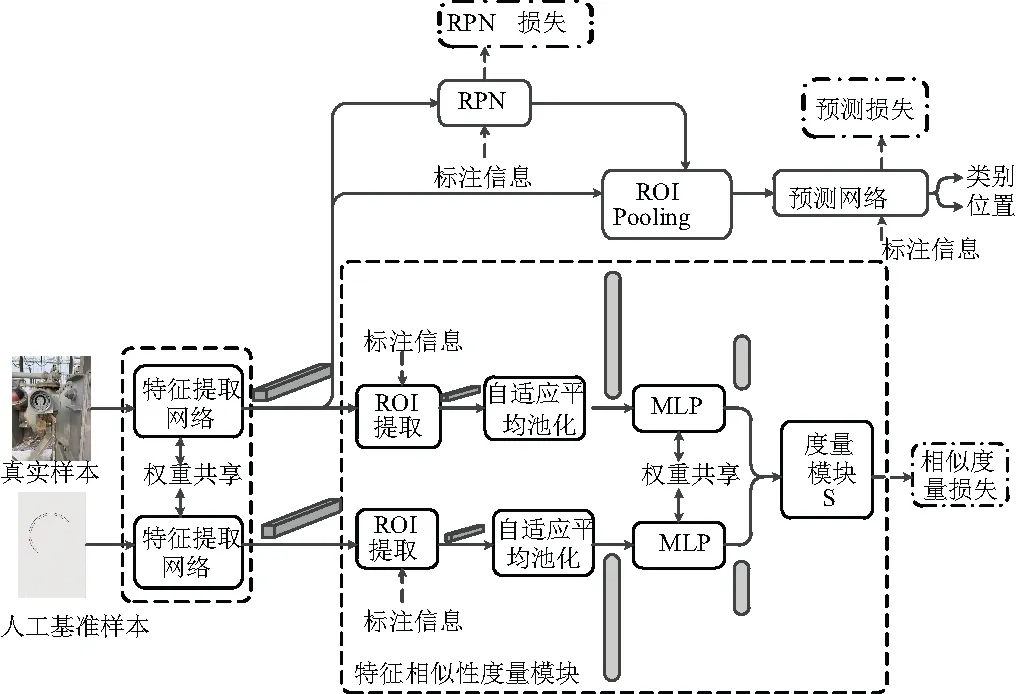
图8 融合相似度量损失的Faster R-CNN结构示意图

表2 特征相似性度量模块网络结构
1.4 相似度量损失
对度量模块而言,尽管其输入向量已经被嵌入低维向量空间,但从图像处理任务的角度考量,输入的低维特征描述向量依然有着较高的维度,而夹角余弦在处理相似性度量问题时,在不同维度下具有相同的判定准则,对维度具有良好的鲁棒性。鉴于此,采用向量之间的夹角余弦作为度量模块S,余弦值越大表明特征描述向量之间的夹角越小,两待比较对象越相似。
(4)
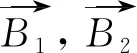
(5)

由于特征提取网络最后使用的激活函数不同,使得特征描述向量元素的取值范围不同,因此采用了不同的误差函数训练网络。分别是:
(1)基于Tanh激活函数对输出向量进行非线性操作。Tanh的值域为[-1,1],经过归一化后特征描述向量元素的取值范围为[-1,1],使得相似度的取值范围S∈[-1,1]。误差函数如下:
(6)
(7)
式中Si为每个图像对之间的相似度得分;NBatch为在训练过程中一个批次(Batch)包含真实图像的个数;Mj为一张真实图像内包含GT_boxes的个数;M为一个Batch中所有GT_boxes的数量。
(2)基于ReLU激活函数对输出向量进行非线性操作。ReLU的值域为[0,∞],经过归一化后特征描述向量元素的取值范围为[0,1],使得相似度的取值范围S∈[0,1]。误差函数如下:
(8)
式中 log()为以自然底数e为底的对数函数。
融合相似度量损失的Faster R-CNN模型的总损失为:
loss=lossRPN+lossFrR+λ·lossS
(9)
式中lossRPN为基线模型中与建议框生成网络(Region Proposal Network,RPN)相关的损失,包括RPN结构的分类损失和回归损失;lossFrR为基线模型中与Faster R-CNN预测器相关的损失,包括预测器的分类损失和定位损失;lossS为相似度量损失,可以取lossR或者lossT;λ为平衡系数,用以维护相似度量损失与原基线模型损失的平衡。
2 实验结果及分析
2.1 实验环境
为便于对该模块定性和定量的分析,采用Faster R-CNN为Baseline,在该模型的基础上验证特征相似性度量模块的有效性。为了说明基于人工-真实样本度量学习的指针式仪表检测算法在少样本情况下的效果,在电力系统的实际生产环境中采集指针式仪表图像构造数据集,包括多种类型的压力表、温度表、电压表、电流表、密度表等,共计220张,囊括了工业生产常见的指针式仪表类型。为了充分说明该方法的有效性,避免产生偶然性因素,通过随机采样,从总数据集中随机采样20张图像作为训练集,剩余200张作为验证集,并每10次训练取平均值作为最终结果。人工基准图像由ABSGA随机生成,通过Faster R-CNN的度量分支参与训练。
文中所有算法均运行在Ubuntu18.04 LTS操作系统下,借助Pytorch神经网络框架,使用Python编程语言实现算法的搭建,并通过CUDA10.1调用NVIDIA 1080Ti专业级显卡进行GPU加速,以期更快地完成训练和测试。
为了量化说明文中算法的有效性,采用目前目标检测模型中常用的评价指标:平均精度均值(mean Average Precision,mAP)对模型进行评估。由于本算法针对的是指针式仪表这一单目标,因此mAP退化为精度均值(Average Precision,AP)。按照目标检测框与真值框间的交并比(Intersection over Union,IoU)不同,AP评价指标可以分为AP50(IoU=0.5计算得到的AP)、AP75(IoU=0.75计算得到的AP)、AP50_95(IoU分别取0.5~0.95,间隔0.05计算的平均AP)。结合文中研究内容,分别对以上三种指标进行比较。
2.2 对比实验
表3给出了融合相似度量损失前后的指针式仪表检测的AP结果,为10次训练和验证后的平均值。训练阶段选择的Batchsize为1,优化器为随机梯度下降(Stochastic Gradient Descent,SGD),初始学习率设为0.005,动量参数设为0.9,学习率衰减为5,最大迭代次数(epoch)为50。检测可视化结果如图9所示,其中x轴为不同的AP评价标准,y轴为在特定评价标准下的AP值。横线柱为基线模型Faster R-CNN的检测结果,纵线柱为融合相似度量损失后Faster R-CNN的检测结果,纵线柱上方的数字表示改进模型相对于基线模型的提升情况。两柱内的散点分别表示10次训练的检测结果。

表3 融合相似度量损失前后的指针式仪表检测结果(10次平均)
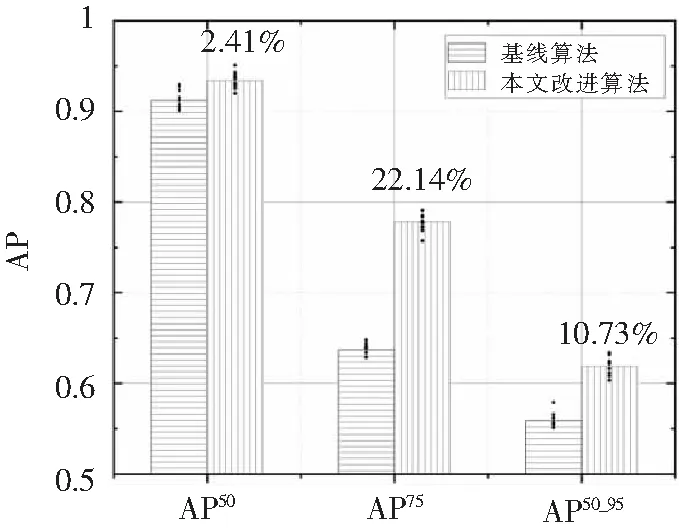
图9 融合相似度量损失前后的指针式仪表检测结果统计图
图10表示指针式仪表检测任务特殊性的示意图。图中框(右)为真值框,框(左)为与真值框IoU=0.643的检测框,按照AP50的评价标准,该框(左)检测框应归为正确检测框。但是,从指针式仪表检测任务的目的来看,检测是为了后续对检出目标进行处理,后续处理的准确度严重依赖于本阶段检测的精度,因此仅仅依赖AP50这种比较松弛的评价标准显然是不合适的,应更加侧重AP75和AP50_95的结果。

图10 指针式仪表检测任务特殊性示意图
结合表3和图9可以看出,对基线模型来说,虽然AP50较高,但AP75与AP50_95较低,鉴于本任务的特殊性,基线模型还是存在较大提升空间的。在融合相似度量损失后,三种性能指标均有所提升,其中AP75提升最为明显,提升幅度高达22.14%,AP50_95也有10.73%的提升。由于基线模型的AP50本身就很高,因此在融合相似度量损失之后AP50的提升幅度最少,只有2.41%。综上可知,融合相似度量损失之后的目标检测模型可以有效利用人工基准样本的引导作用,通过在低维向量空间中进行相似性度量,降低模型对数据集样本数量的要求,有效缓解了真实场景中指针式仪表样本缺少的问题。
为全面评估基于人工-真实样本度量学习的指针式仪表检测模型性能,文中比较了SSD512[28]、Cascade RCNN[29]、Faster R-CNN[30]、RetinaNet-101[31]、改进的YOLOv3[22]、改进的YOLOv4-Tiny[32]以及文中算法的检测效果,如表4所示。

表4 不同检测方法性能对比
由表4可知,相较于其他模型,基于人工-真实样本度量学习的指针式仪表检测模型在三种指标上都有较大的提升,其中AP75提升最为明显。与RetinaNet-101相比,AP75提升幅度高达86.57%。由此可以看出文中算法在处理少样本数据的优势。
图11给出了融合相似度量损失前后的Faster R-CNN模型在进行指针式仪表检测后的定性可视化结果。可以看出,基线模型在检测指针式仪表时,容易出现以下问题:预测框过大,如图11(a),虽然完全包括检测目标,但是由于预测框过大,包含的干扰信息占比增加,对后续指针式仪表读数的识别非常不利;预测框与真实目标交并比较小,指针式仪表未完全标出,如图11(b),无法进行后续仪表读数识别;出现较多误检测,如图11(c)和图11(d),将其他物体错误预测为目标。针对以上问题,本文融合相似度量损失的Faster R-CNN模型有很好的改善效果,通过引入人工基准图像,使得特征提取网络在训练阶段得到引导,有效提升指针式仪表的检测精度,如图11(e),有效提升检出目标的完整率,如图11(f),并有效抑制误检,如图11(g)和图11(h)。从以上结果来看,充分验证了文中算法的有效性。
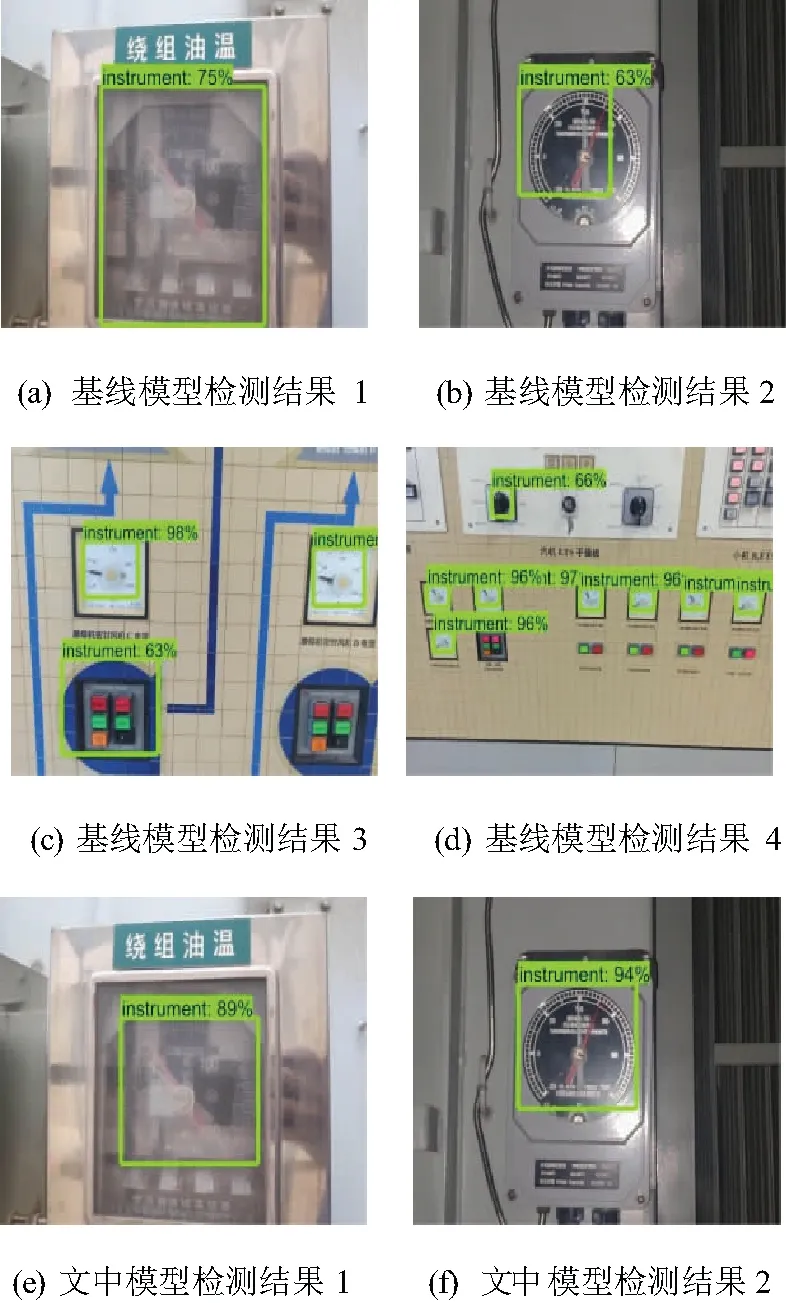

图11 融合相似度量损失前后的指针式仪表检测可视化结果
2.3 消融实验
为了深入理解特征相似性度量模块在本算法中的作用,通过修改部分超参数进行消融实验,包括损失函数、相似度量损失在Faster R-CNN总损失中的比例λ及特征描述向量维度D。
表5和图12是在采用D=256、λ=0.2时,对损失函数进行消融实验的结果。

表5 损失函数消融实验结果

图12 损失函数消融实验结果统计图
由表5和图12可以看出,在其它参数不变的情况下,很明显基于ReLU激活函数的损失lossR要比基于Tanh激活函数的损失lossT效果更优。相比lossT,基于lossR的AP50、AP75、AP50_95分别有1.52%、12.75%、7.84%的提升。
表6和图13是在采用lossR作为损失函数、D=256时,对相似度量损失在Faster R-CNN总损失中所占比例λ进行消融实验的结果。由表6和图13可以看出,在其它参数不变的情况下,随着λ的增大,AP50、AP75及AP50_95的变化趋势大致相同,都是先增大后减小。除λ=10.0,其他λ情况下三项指标均有提升,在λ=0.2时三项评价指标均较高,其中AP75和AP50_95达到最高,AP50达到次高,只比最高值低0.5%。在λ=10.0时,除AP50有较少的提升外,AP75和AP50_95都有所下降。综合来看,相似度量损失的加入使模型的精度有较大的提升,引入损失的比例决定着精度提升的幅度,过小或过大的比例会使精度提升较小,更大的比例会使系统失去平衡,精度不升反降。
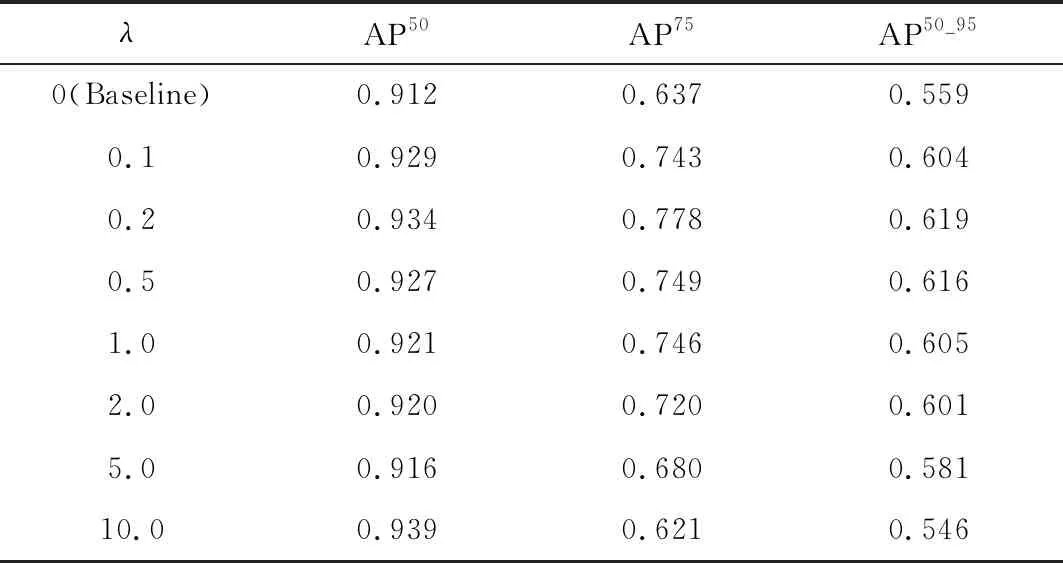
表6 λ消融实验结果

图13 λ消融实验结果统计图
表7和图14是在采用lossR作为损失函数、λ=0.2时,对特征描述向量维度D进行消融实验的结果。由表7和图14可以看出,其它参数不变的情况下,随着D的变化,AP50和AP50_95变化不太明显,分别只有1.6%和1.9%的变化幅度;而AP75的变化幅度较大,在D=256时该指标达到最大,D=1 024时最小。随D的增大,三个指标都有先增大后减小的趋势,同时在D=256时达到最优。综上所述,特征压缩维度D对AP75指标影响最为明显,对另外两个指标影响较小,并且使用过低的特征压缩维度会因丢失过多信息导致精度下降,过高的特征压缩维度会引起特征冗余,不仅不能提高检测精度,且会使计算量增大。
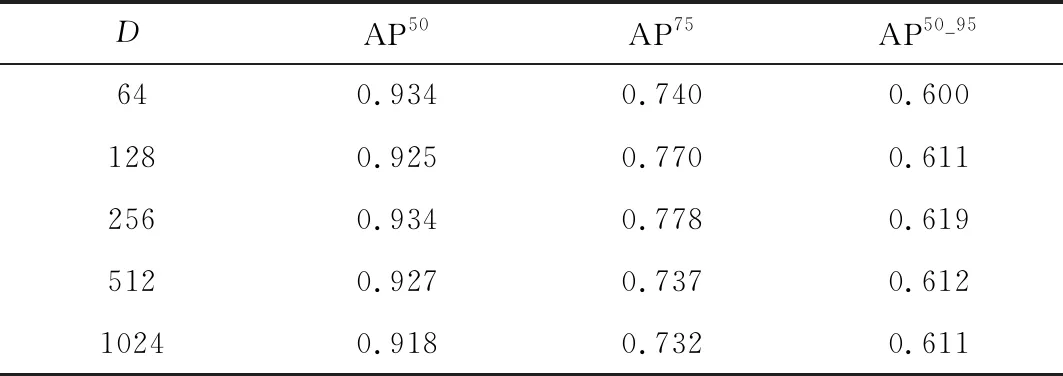
表7 D消融实验结果
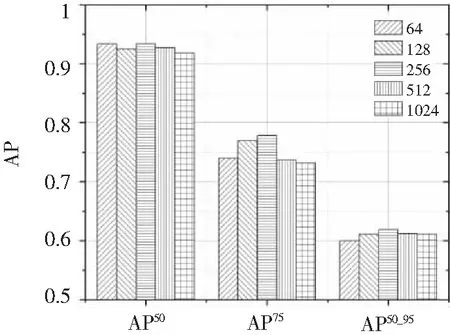
图14 D消融实验结果统计图
3 结束语
在对指针式仪表结构充分分析的基础上,结合度量学习的特性,提出了基于人工-真实样本度量学习的指针式仪表检测模型。通过对指针式仪表显著特征区域进行建模,并以此生成人工基准图像,在相似度量损失函数的驱动下,利用人工基准图像对特征提取网络进行先验指导。通过对比实验,基于人工-真实样本度量学习的指针式仪表检测模型在进行指针式仪表检测任务上,相对于基线模型,AP50、AP75、AP50_95分别有2.41%,22.14%,10.73%的提升,其中AP75提升最为显著。
实验表明,将度量学习引入目标检测模型,有利于缓解人工图像与真实图像之间的分布差异,并且可以在先验人工图像的指导下对特征提取网络进行校正,提升模型的检测能力,缓解了指针式仪表检测精度对训练样本数量的严重依赖,有效提升了少样本情况下指针式仪表的检测精度。
