基于改进粒子群优化算法的负荷分配方法研究

2022-10-11魏家柱潘庭龙

电测与仪表 2022年10期

魏家柱，潘庭龙

(江南大学物联网工程学院，江苏无锡 214122)

0 引言

电力经济调度问题可以归纳为如何进行负荷分配，实现总煤耗最低。然而，单纯追求经济效益已经不能满足新形势下电网建设的需要。随着人们环保意识的提高，污染物的排放量正成为衡量电力系统调度优良性的重要指标之一。由此引出环保经济发电调度(Environmental-Economic Dispatch, EED)的多目标优化问题。

当前在研究EED问题时主要有3类方法：文献[1-2]中的多目标问题转化为单目标问题求解。文献[3-4]的多目标优化算法直接求解，文献[5]中的单个目标转换为约束条件求解。文献[1]在容量优化分配问题中引入了模糊集理论，将多个目标函数整合得到单个目标函数并进行优化，对不同权重下的计算结果进行对比，选取最优的满意度，使得火电机组的出力曲线更为平滑，保证自动发电控制系统的经济、环保运行。文献[2]在微电网并网运行时，综合考虑需求侧响应建立多目标优化模型，利用层次分析法将该多目标优化问题转化为单目标优化问题，使得运行过程中的成本有所降低。文献[1-2]只在特定的权重组合下说明文章算法的先进性，缺乏和多目标优化算法的对比。而多目标优化算法则有效避免了对各个子目标权重组合的选择，一次性地给出多个Pareto最优解，能够很好地保证决策者的选择空间，简化计算过程。为了找到更加真实的Pareto解集并维护解集的多样性，文献[3]针对机组启停和负荷分配的综合模型，在非支配排序遗传算法II的基础上引入了0-1混合变量动态求解该多目标优化问题。文献[4]为了降低帕累托锋的产生和满意解的选择带来的计算复杂性，通过混合混沌微分进化算法和鲍威尔模式搜索算法的实现，得到了多目标火电负荷调度问题的满意解。粒子群优化算法原理相对简单，迭代过程中不会出现交叉和变异，只要设定搜索范围和全局最优位置，就可以计算出优化问题中的最优解，因而在负荷优化分配问题中得到了广泛的应用[6-8]。

而常规的多目标粒子群优化(Multi Objective Particle Swarm Optimization,MOPSO)算法在求解EED问题时容易陷入局部最优且难以保证求解结果分布的均匀性。在利用MOPSO求解EED问题时引入了精英交叉算子，并通过拥挤度排序的方法保留较好的粒子，同时在精确计及网损时给出了等式不等式约束的处理方法。

1 负荷分配的多目标优化模型

1.1 经济性单目标函数

在对出力进行调节时，机组既发出有功功率又发出无功功率。其中无功功率对机组的煤耗量影响较小，利用二次函数拟合机组煤耗量和承担的有功负荷总量可以得到发电总成本的目标函数为：

(1)

式中Pi为第i台机组发出的总功率(MW)；N是参与电力系统调节的机组总数；ai、bi、ci是机组的煤耗量系数，由机组的自身特性决定。

1.2 环保性单目标函数

燃煤过程中主要排放SO2、CO2和NOx三种气体，其中SO2和CO2的排放量较低，可以忽略。用三次函数来拟合NOx排放量和机组承担的有功负荷之间的关系，则NOx排放量函数可以表示为：

(2)

式中αi、βi、γi和λi是机组的污染物排放系数，由机组的自身特性所决定。

1.3 约束条件

(1)考虑到整个互联电力系统的安全，机组在输出功率时首先要满足系统的功率平衡约束条件。互联电网机组出力的功率平衡约束条件为：

(3)

式中PD表示电力系统的负荷需求；PL表示电力系统的网络损耗。其计算公式为：

(4)

式中B、B0、B00为网损系数。

(2)为了保证机组的稳定运行，机组出力大小需限制在一定范围内。互联电网机组出力的的不等式约束为：

Pmini≤Pi≤Pmaxi, (i=1,…,N)

(5)

式中Pmaxi为机组i的有功出力上限；Pmini为机组i的有功出力下限。

2 基于改进粒子群优化算法的EED问题求解

2.1 约束条件的处理

(1)等式约束

在设定机组出力的等式约束时，一些文献直接忽略了网损[1]。还有另外一些文献为了处理方便，只考虑了B项系数[9]，这样都会造成优化结果存在误差。为使求解结果严格满足发电机出力等式不等式约束条件，在粒子初始化位置和更新位置时选取机组1作为等式约束平衡机组。

由式(3)和式(4)可以得到：

(6)

选取机组1作为平衡机组时，将式中机组1的出力分离开来可以得到：

(7)

又因为网损系数中存在BT=B，故存在：

(8)

将式(8)带入式(7)中并合并同次幂，可得到：

(9)

(2)不等式约束

粒子在进行位置更新时，可能会飞离限定的区域。对于求解结果需要判定是否满足1.3节中的不等式约束条件。粒子第i维度的大小Xi在不满足约束条件时根据式(10)进行更新[8]：

(10)

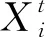
而机组1的出力是由式(9)确定的，作为平衡机组其出力必须满足不等式约束条件。若不满足，应该通过设置不满足条件使得粒子重新开展此次循环，直到1机组的出力满足不等式约束条件。

在初始化粒子位置和更新粒子位置时处理其等式和不等式约束的一般流程图如图1所示。

图1 等式不等式约束处理方法示意图

具体步骤为：

Step 1:位置初始化时按照初始化公式确定机组2,…,N出力，位置更新时按照粒子群优化算法的位置更新公式更新机组2 ,…,N出力；

Step2:按式(10)约束机组2,…,N的出力；

Step3:按式(9)更新机组1的出力；

Step4:按式(5)判断机组1的出力是否满足机组1的出力不等式约束条件，若满足跳出此次位置更新过程，若不满足返回Step1重新更新所有机组出力大小，直到所有机组同时满足出力不等式约束条件时跳出粒子位置更新循环程。粒子位置每更新一次，等式不等式处理过程同步进行一次。

2.2 寻优参数设置

一个优化算法的好坏的关键在于能否权衡全局以及局部搜索，粒子群优化算法全局以及局部搜索受到惯性权重w设置的影响。动态改变w，可以加快粒子群算法的收敛速度。现阶段普遍采用的三者独立的调整策略削弱了粒子群算法在进化过程中的统一性。根据惯性权重的变化规律，采用了惯性权重w、学习因子c1、c2的联动策略，具体为：

(11)

式中wmax和wmin分别表示权重因子的最大和最小值；Tmax表示最大的迭代次数。

2.3 精英交叉算子

传统粒子群优化算法中的粒子只学习最优粒子中的飞行经验，而没有参照其他粒子的经验。这样的一大缺陷在于粒子的多样性优势难以发挥，很可能会陷入早熟。且在初始化粒子时存在相似粒子，会出现收敛速度慢，易陷入局部最优等问题[10]。交叉操作则能很好地解决该问题，交叉操作一方面能够使得粒子进行信息交换，另外一方面使得优秀的基因得以保留。为了使MOPSO尽快跳出局部最优，本文将精英交叉算子[11]引入MOPSO之中。即在每次更新粒子位置后，产生一个随机数a，如果a小于默认的交叉概率pc，则利用更新后的所有粒子中适应度最好的两个粒子生成两个新的粒子，新产生的两个粒子将替换更新后适应度最差的两个粒子并参与循环更新过程。新粒子的计算公式为：

(12)

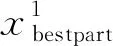
2.4 外部档案维护策略

外部归档集的作用为储存粒子在更新过程中所探索到的非支配解。寻优过程开始前，在外部设置归档集，其大小和粒子大小相同。循环过程正式开始之前即将非支配解集全部存储到归档集中。每次循环结束，都将排序较高的粒子放入归档集中。循环次数到达上限时，归档集中存放的结果就是该经济环保负荷优化分配问题的Pareto解集。

由于循环结束后排序较高的粒子会不断地写入档案，而归档集的容量有限，当写入粒子的数量大于档案规模时应该删除排序较低的粒子，并再次重新排序，重复上述操作得到排序较高且和种群规模相等的外部归档集。一般认为，求解结果分布范围广且分布均匀视为优化效果较好。为了保证最终的Pareto解集分布的广度和均匀性，本文将非支配排序遗传算法(NSGA-II)中按照拥挤距离排序的方法引入到粒子群优化算法中来求解经济环保负荷优化分配问题。

设定任一粒子的初始拥挤距离为0，单个目标拥挤距离的计算方法如下[13]：

(1)将归档集中的各粒子依次按照某一目标进行升序排序；

(2)为了让粒子更能向排序在两端的地方飞行，定义边界点的拥挤距离大小为无穷大；

(3)按照公式(13)计算各个体的拥挤距离。

L[j]d=L[j]d+(L[j+1]i-L[j-1]i]/(fmaxi-fmini)

(13)

式中L[j+1]i表示第j+1个粒子的目标函数i的值;fmaxi和fmini则分别表示各个粒子下目标函数i的最大值和最小值。

对于多个目标函数均执行(1)～(3)中的过程，得到所有粒子的拥挤距离，并将其从大到小排序。

2.5 求解EED问题时总体运算流程

根据以上思路，改进后的粒子群算法在求解负荷优化分配问题时的一般流程如图2所示，整个过程的实现均依靠机组的本地控制器。

具体步骤为：

Step1:在机组2 ,…,N承担的负荷界限内随机选取Q个点作为粒子初始位置。为了加速寻优过程，初始化公式为[13]：

Pi=Pmini+(Pmaxi-Pmini)×rand(i=2,...,N)

(14)

图2 改进后的粒子群优化算法的流程图

按照2.1节中的所提方法处理机组1的出力大小，粒子初始化为Q行N列的矩阵;

Step2:定义同时存放机组出力大小，经济及环保性能指标和拥挤距离的矩阵，则该矩阵的维度为N+2+1；

Step3:对外部归档集进行初始化，选取非支配解集进入速度位置更新的循环中;

Step4:循环开始，按照2.4节中的方法计算非支配解集中各粒子经济环保目标函数的拥挤距离，并从大到小排序;

Step5:拥挤距离前10%的粒子中随机选取一行作为全局最优位置，此时的最优位置处于比较分散的区间，能够很好地提高算法的全局寻优能力;

Step6:逐行更新粒子的速度和位置，公式为：

(15)

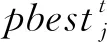
按照2.1节中的所提方法处理机组1的出力大小;

Step7:引入2.3节中的交叉算子，生成新粒子;

Step8:按照2.4节中的所提方法维护外部档案，防止写入外部档案中的粒子溢出;

Step9:当前粒子支配个体最优粒子时则用当前粒子替代个体最优粒子，否则不操作；

Step10：若迭代次数不满足则回到Step4；迭代次数满足后输出外部档案，得到多行N+2+1列的矩阵。

3 实例分析

将所提的负荷分配方法在三机组上进行测试，其对应的特性参数[14]如表1所示，网损系数如下：

由表1可知扰动出现前3机组承担的总负荷大小为908.06 MW，而扰动出现后调度中心所给指令值大小为1 200 MW，为了避免各机组反向调节，设置当前机组的出力作为出力下限，计煤耗的单价为71 $/t。考虑忽略和计及网损两种情况下经济环保负荷分配的结果，每种情况下均用文献[15]中的标准MOPSO和本文所提的的IMOPSO分别求解。为了保证求解结果的公平性且简化获取最终分配结果的工作，四次求解的算法粒子大小均为50个，迭代次数均为20次。改进前c1=c2=2，w=1，改进后wmax=0.9，wmin=0.4，引入的精英交叉算子中交叉概率pc=0.8，从适应度最好的粒子中继承的比例b=50%。

在忽略和计及网损两种情况下，利用所提的粒子群优化算法和常规的粒子群优化算法得到的Pareto最优解集分别如图3和图4所示。

图4 计及网损时的Pareto最优解集

分析图3和图4中的结果可以发现引入精英交叉算子后Pareto解集的大部分点在改进前的下方，只在经济成本较高的一段才重合。这说明精英交叉算子的引入很好地增强了粒子的多样性，使其很快的跳出了局部最优，克服了常规粒子群优化算法求解高维粒子容易陷入局部最优的缺陷。此外，引入的拥挤度排序的方法使得求解结果在分布上更加均匀，和改进前相比能够为决策者提供更大的决策空间。

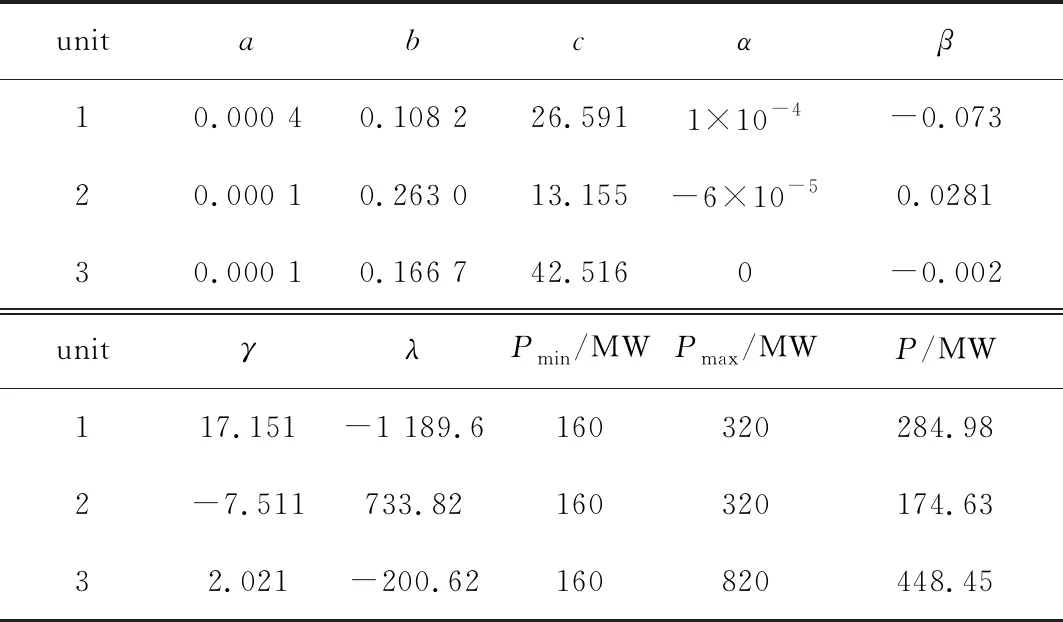
表1 3机组特性系数

在实际优化配置过程中，最终实施的方案一般只有一个。利用文献[16-19]中的模糊隶属度函数筛选各种情型下的Pareto解集，得到的该经济环保负荷优化分配的最终解如表2所示。该求解结果包括经济成本Fe、污染物排放量Fg、各机组出力大小Pi，并进一步计算各机组出力之和P∑以及网损PL。

分析表2中结果可以发现，同样在Pareto解集中利用模糊隶属度函数对求解结果进行筛选，忽略网损时粒子群优化算法在改进后使得发电成本降低了7 $/h，污染物排放降低了5.432 3 t/h。计及网损时粒子群优化算法在改进后使得发电成本降低了174 $/h，污染物排放降低了11.041 8t /h。该结果表明，所提算法在忽略和计及网损两种情况下都能较好的适用于经济环保负荷多目标优化分配问题中。

同在算法改进后，计及网损时和忽略网损时相对比经济成本和污染物排放分别上升了1 894 $/h和30.722 8 t/h，该结果说明所研究的电力系统中网损对优化结果影响较大，进一步论证了给出精确计及网损时等式约束不等式处理方法的必要性。