基于多维缩放的日负荷曲线聚类分析

2022-10-11徐毅吴鸣李广玮王昕扬

电测与仪表 2022年10期

徐毅，吴鸣，李广玮，王昕扬

(1.上海电力大学电子与信息工程学院，上海 200090； 2.中国电力科学研究院有限公司，北京 100192)

0 引言

近年来，随着智能电网的深入和推进，越来越多的高级量测体系(Advanced Metering Infrastructure,AMI)投入运营中，电力负荷数据变得易于感知和测量，为电网公司提供了海量的用户负荷数据[1]。通过聚类技术可以从大量的用户负荷数据中挖掘出其典型的用电特征，能够为电网公司实现负荷预测[2]、需求侧管理[3]等方面提供强有力支撑。因此研究合理准确的负荷曲线聚类方法具有十分重要的现实意义。

目前国内外对负荷曲线的聚类大致上可分为直接法和间接法[4]。直接法是对经采集过的负荷数据直接进行聚类，常见的聚类算法有K-means[5]、FCM、SOM等。但随着负荷数据规模的不断增长，直接法带来了存储和计算效率的双重挑战。

间接法可以解决这一矛盾。间接法是指先提取负荷曲线的特征，再根据其特征进行聚类分析。间接法可分为变换和降维两种方法。常见的变换方法有离散小波变换[6]、离散傅里叶变换[7]等。降维是指将负荷数据维数进行降低，再进行聚类。例如文献[8]采用了6个有明确物理意义的特征指标作为负荷曲线降维的依据，再利用加权K-means聚类方法进行聚类。文献[9]采用主分量分析方法得到日负荷曲线的部分主要特征作为降维聚类的指标，再利用加权K-means方法进行聚类。文献[10]采用奇异值分解方法将数据旋转变换至新的坐标系中，然后将各坐标轴上的坐标作为降维指标，再利用改进的K-means方法进行聚类。文献[11]采用SAX算法对负荷曲线进行降维并提取特征，再运用改进AP聚类算法对负荷曲线进行聚类。文献[12]采用主成分分析进行降维，再用四种聚类方法进行聚类，最后用共识矩阵对各聚类成员进行聚类融合。

上述选取的不同降维方法虽然都能进行有效的聚类，但在聚类过程中均存在两个问题：(1)采用降维破坏了原本曲线之间的差异性，对原始曲线信息造成一定程度损失，可能会导致原本被分成一类的曲线通过降维被分成不同类别，进而会对曲线聚类的准确度造成影响；(2)通过降维得到的指标是有重要程度之分的，需要对其进行权重配置。

多维缩放(Multi-Dimensional Scaling，MDS)是一种典型的降维算法，它是保持了样本在原始空间和低维空间的距离不改变为原则，最大程度地减小了数据“失真”的现象[13]。这样可以很好的解决因降维后所导致的样本间差异性降低的问题。

1 负荷降维聚类理论

1.1 MDS理论

假设有n个用户，每个用户采集到m维数据，可以计算出在原始m维空间中的距离矩阵D∈Rn×n(这里采用欧式距离)，其中dij表示第i个用户和第j个用户之间的距离。若把数据降维到q维空间中去，得到所有用户点在q维空间中的表示为矩阵Z∈Rn×q，其中第i行数据zi=[zi,1,zi,2,…,zi,q]表示第i个样本，并且任意两个用户在q维空间中的距离等于原始空间中的距离。由此，可推导出满足此条件矩阵Z的解析解[14]。

由保持距离原则可知：

(1)

假设低维空间中的样本是中心化的，即：

(2)

对式(1)左右两边求和有:

(3)

(4)

(5)

定义内积矩阵B=ZZT∈Rn×n，bij是矩阵B中第i行第j列的元素，即bij=zizTj。则由式(1)可知：

(6)

由式(2)～式(6)可得

(7)

对矩阵B做特征分解，得到：

B=VΛVT

(8)

式中Λ是由B的特征值生成的对角矩阵；V是特征向量作为列的矩阵。

由矩阵B的定义则有：

(9)

为了能实现降维，往往仅需降维后的距离与原始空间中的距离尽可能接近，而不必严格相等。若降到q维空间中去，则选取前q个最大的特征值及其所对应的特征向量，得到Λq和Vq，则降维后的特征表示为：

(10)

1.2 降维指标数目的确定

求出矩阵B的特征值并按照从大到小(取前m个)排列为：λ1≥λ2≥…≥λq…≥λm

定义sq为累计贡献率，其公式如下：

(11)

累计贡献率越大，则说明降维后的矩阵保留了越多的信息。通常累计贡献率达到95%即可确定降维的数目。

2 基于MDS的负荷聚类算法

2.1 数据预处理

文中据预处理包括异常数据处理、数据归一化处理和曲线平滑处理三部分。

2.1.1 异常数据处理

在数据采集的过程中，由于数据传输、装置故障、线路等问题会产生异常数据[15]。对异常数据需要通过负荷变化率来判别，当某条日负荷曲线的数据异常量超过10%时，需剔除；若小于10%时，则通过均值替换法进行修正。其计算方式如下：

设第i条曲线的第k个数据值xi,k为异常数据点，修正值为：

(12)

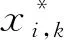
2.1.2 数据归一化处理

由于采集到的日负荷曲线数据之间存在较大的差异，为消除负荷数量级对聚类效果的影响，因此要对数据进行归一化处理。

通过归一化可将用户负荷特性数据压缩在区间[0,1]中。文中用极值归一化方法，表达式如下：

(13)

式中x(i,k)是经采集过的第i条用电曲线在第k点的负荷数据;x′(i,k)是经归一化后的第i条用电曲线在第k点的负荷数据；x(i)max和x(i)min是第i条负荷曲线的最大、最小用电量。

2.1.3 曲线平滑处理

电网在实际运行时由于受到通信中断、软硬件故障、信号干扰等影响会使得负荷数据产生失真情况，导致负荷曲线出现较大波动，从而影响聚类结果。而高斯滤波法可以更有效地“消除干扰”，进一步突出曲线形状，反映出曲线的总体趋势[16]。故采用高斯法处理数据，经过处理前后的负荷曲线如图1所示。

图1 负荷曲线的平滑处理

2.2 加权K-means聚类

2.2.1 基于CRITIC—熵权法的指标权重配置方法

基于MDS的理论，若降低到q维空间中去，则取出前q个最大的特征值。这说明特征值的大小反映出了该维空间的重要程度，也同时说明降维指标是有重要程度之分的。若将降维后的矩阵直接进行K-means聚类，则会忽略降维指标的重要程度，将在很大程度上影响负荷聚类质量。故需要进行降维指标权重配置。

单一的CRITIC法未能考虑指标间的差异性对指标权重的影响，而熵权法则是充分运用指标的数据信息的差异来确定指标权重，可以弥补这一不足；但是单一的熵权法又容易受到指标数值变动的影响，指标值的变动很小或者很突然地变大变小会使得熵权法用起来有局限。故本文将两种方法相融合，优势互补，构建了基于CRITIC—熵权法的指标权重配置方法[17]。

设降维后的矩阵Z=(zij)n×q，i=1,2,…,n;j=1,2,…,q。则熵权法步骤如下：

(1)计算信息熵

(14)

(15)

式中Pij是第i个用户在第j个降维指标下的贡献度；Ej是第j个降维指标的信息熵。

(2)确定权重

(16)

式中wj是第j个降维指标的权重。

CRITIC法步骤如下：

(1)计算指标信息量

(17)

式中Cj是第j个降维指标所含有的数据信息量；δj是第j个降维指标所含有的数据标准差；rkj是k、j两个降维指标之间的相关系数。

(2) 确定权重

(18)

进而得到降维指标的综合权重为：

(19)

由此即可确定权重向量W=[W1,W2,…,Wq]。

2.2.2 改进的K-means聚类方法

以降维后的矩阵Z为输入，以欧式距离作为相似性判据，进行聚类，其处理过程如下：

Step2：样本分类。计算每条日负荷曲线到K个子聚类中心的加权欧式距离，再将该条日负荷曲线划分到距离它最近的子聚类中心。从样本zi到第j个聚类中心zj=[zj,1,zj,2,…,zj,q]的加权欧式距离可由式(20)计算：

(20)

Step3：更新聚类中心。根据Step2中所得到的结果，对每个类簇中的所有日负荷曲线求取平均值，并将其作为各类簇的新聚类中心；

Step4：迭代计算。计算聚类中心是否收敛，若未收敛则跳转至Step2，重复步骤Step2和Step3；若收敛则算法结束。

2.3 聚类有效性评价指标

聚类有效性检验是使用聚类有效性指标，对聚类后的结果进行评价，以此来明确最优类簇数的过程[18]。常见的聚类有效性指标有轮廓系数(Silhouette Coefficient, SC)、CHI指标(Calinski-Harabasz Index，CHI)、戴维森堡丁指数(Davies-Bouldin Index，DBI)。

由于SC是通过极值点来判断最优类簇数，而极值点相比较于拐点从视觉上更易觉察出；此外SC的内聚度指标和分离度指标使用的是样本的平均欧式距离，稳定性强，不易受到类簇中心干扰，所以采用SC作为聚类有效性指标[19]。

设曲线被分成K个类簇U1,U2,…,UK，当计及权重向量W时，则对于第i个样本其对应的向量修正轮廓系数为：

(21)

其中：

式中a(i)为i向量到同一簇内其他点不相似程度的平均值，该值越小，簇内越紧凑；b(i)为i向量到其他簇的平均不相似程度的最小值，该值越大，簇间分离程度越高。

将所有样本的轮廓系数求平均值，就是该聚类结果的总轮廓系数Sn(i)：

(22)

Sn(i)可用于评估聚类的总体质量，其值越大就表明聚类的效果越好，对应于最大值时的聚类数目K就是该聚类结果的最优类簇数。基于MDS的负荷聚类算法的流程图如图2所示。

图2 基于MDS的负荷聚类流程图

3 算例分析

3.1 数据集来源

文中实验数据集来自于SEAI发布的爱尔兰智能电表实际测量数据，其覆盖了2009年～2011年6 369个家庭用户及中小型企业用户，负荷数据每30 min采集一次，每个用户每天共采集48个数据点[20]。

3.2 电网实际日负荷曲线聚类

本文共选取2 945户负荷数据作为样本进行实验，经过数据预处理后，最终获得了共计2 732条有效的日负荷曲线，构成了2 732×48阶矩阵A。

采用MDS降维并求累计贡献率sq，如图3所示。

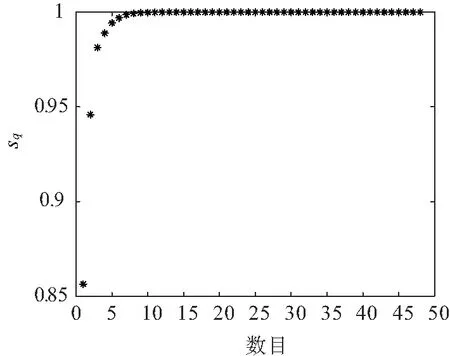
图3 累计贡献率

由图3可知，当降维指标数目达到3时其累计贡献率可达到95%以上，故选取降维指标数目q=3，由此得到2 732×3阶降维矩阵Z。再经熵权法确定权重，得权重向量W=[0.780 6,0.084 5,0.134 9]。采用改进K-means算法对矩阵Z进行聚类，经过计算得出总的轮廓系数Sn(i)和聚类数目K之间的曲线如图4所示。

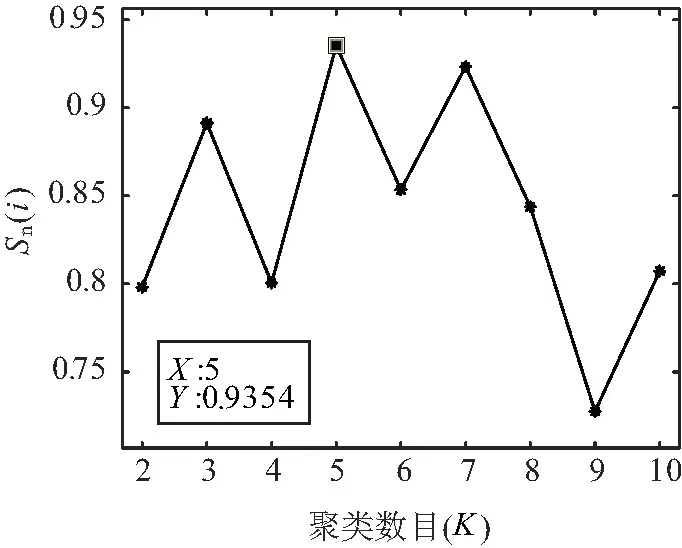
图4 基于MDS降维的聚类指标曲线

由图4可知当K=5时，Sn(i)取最大值为0.935 4，此时聚类效果最好，故最优类簇数为5。这时得到的日负荷曲线聚类结果如图5所示。

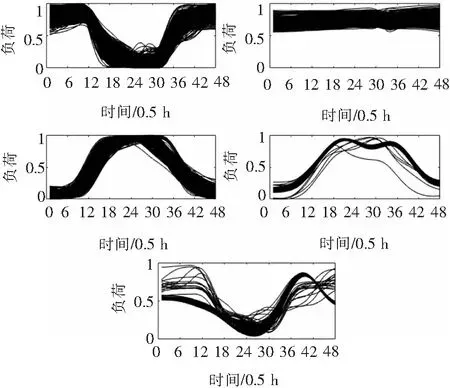
图5 基于MDS降维的日负荷曲线聚类结果

计算每类簇中所有日负荷曲线的平均值，并将其作为该类簇负荷的典型日负荷曲线，则得到的结果如图6所示。

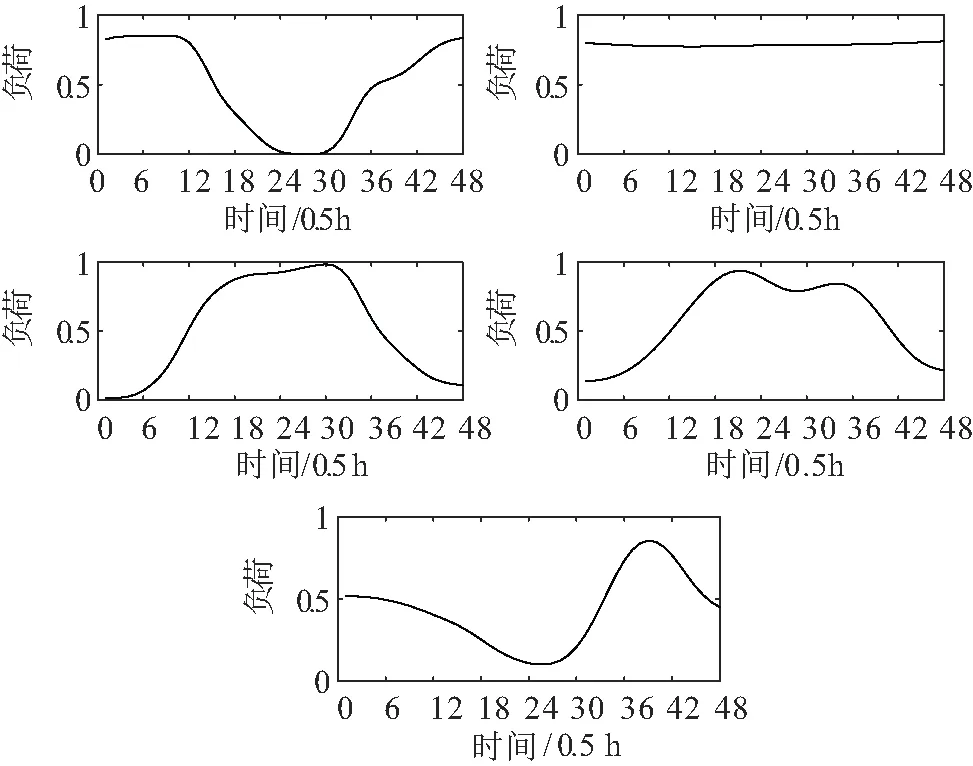
图6 基于MDS降维的典型日负荷曲线图

在图6中，各类簇曲线按照顺序依次呈避峰型负荷、平稳型负荷、单峰型负荷、双峰型负荷和错峰型负荷。在聚类结果中属于各类簇的曲线数目依次为566，222，819，220和605。

类簇1为避峰型负荷，主要用电量在18：00-次日6：00期间，这类负荷主要是夜间营业用电量大，符合酒店、酒吧、KTV等的用电特征。类簇2为平稳型负荷，全天用电量较为平坦，这类负荷应为一些保障民生生活类的负荷，全天无休，如供电、供暖等。类簇3为单峰型负荷，表现为在白天9：00-17：00期间用电量大，负荷曲线较为平滑，这类负荷包括学校、医院、办公楼等。类簇4为双峰型负荷，两个负荷峰期集中在9：00-12：00和14：00-17：00期间，多为政府机关、企事业办事机构等行业性用户。类簇5为错峰型负荷，主要用电量在0：00-6：00和15：00-24：00期间，在凌晨左右有小范围的波动，所以主要呈夜间用电特征，这类负荷主要为家庭用户白天不在家用电在晚上，同时符合一些用电量大的企业利用峰谷电价在电价低谷时安排企业进行生产的习惯。

各类簇曲线走势符合数据集的特征，故基于MDS降维的聚类算法能够较为准确地对日负荷曲线进行分类，分类结果较为合理。

3.3 与传统K-means聚类算法的对比

将原始数据经数据预处理及曲线平滑处理后，直接采用以48个数据点的数据为输入，利用传统K-means算法进行聚类。此时得出总的轮廓系数Sn(i)和聚类结果分别如图7、图8所示。

图7 基于K-means降维的聚类指标曲线

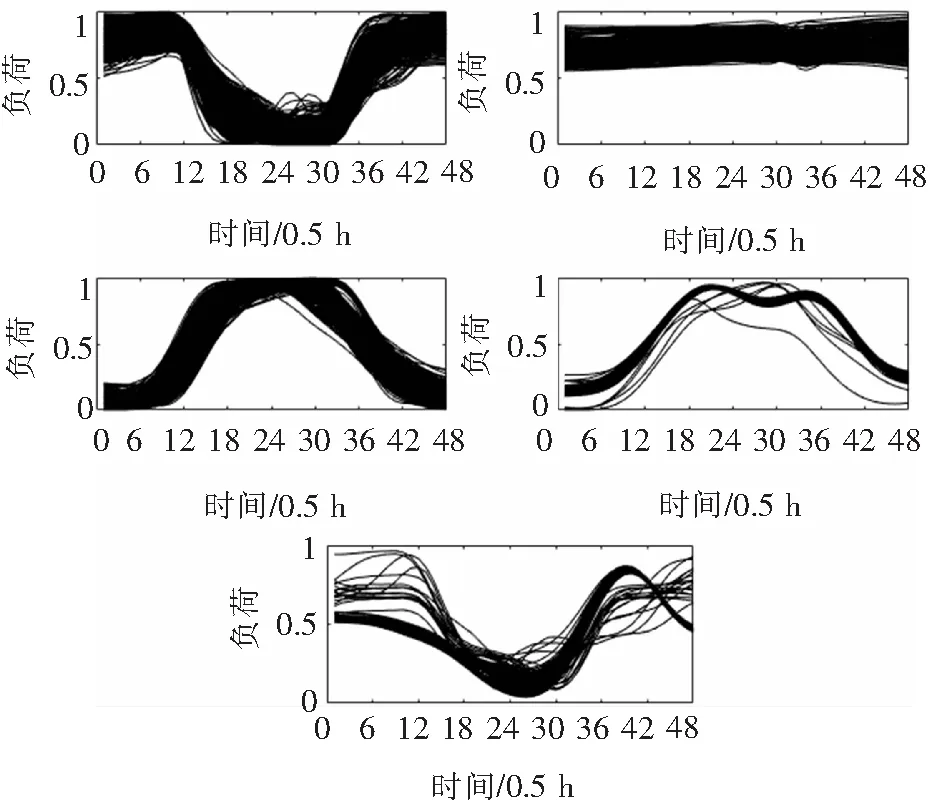
图8 基于K-means降维的日负荷曲线聚类结果

此时得到属于各类簇的曲线数目依次为570，222，815，224和601。与采用MDS降维聚类的结果相比可知双峰型负荷和错峰型负荷显得杂乱无章，

负荷曲线不平滑。

将使用MDS降维聚类得到的轮廓系数、运行时间等数据和采用传统K-means聚类算法得到的运行数据作对比，结果见表1所示。

表1 MDS算法和k-means算法聚类结果对比

由表1可知，两种算法的最优类簇数都是5，说明分类数目选择合理。在采用MDS降维算法时的总轮廓系数Sn(i)略大于传统K-menas聚类算法，则前者的聚类质量优于后者，这是因为采用MDS降维提取出负荷最本质的特征，忽略了无关紧要的信息的干扰，同时也说明了采用MDS降维聚类的准确度高于采用传统K-menas聚类。MDS降维聚类算法的程序总运行时间约为传统K-menas聚类算法7/11。因此，使用MDS降维聚类算法的分类数选择准确，分类结果合理，并且在聚类准确度和聚类时间两方面均优于传统K-means聚类算法。

综上，MDS降维聚类算法较传统K-means方法更能准确地反映用户的功耗特性，具有更好的技术应用价值。