基于虚拟同步机的微电网分布式一致性经济控制策略

苏晨，吴在军，窦晓波

(东南大学 电气工程学院， 南京 210096)

0 引 言

为了提高可再生能源利用率，微电网多利用逆变器作为接口，实现各类分布式电源(Distribution Generator，DG)的集成。为保证系统稳定运行，微电网的控制架构主要由底层逆变器控制和上层协调控制两大块构成。微电网孤岛运行中逆变器多应用下垂控制算法[1-3]，为系统提供电压、频率支撑。然而其惯性小且响应速度快，对系统稳定运行不利。

为了弥补下垂控制转动惯量低的不足，有学者参考传统的同步发电机运行外特性，研究拓展了虚拟同步发电机(Virtual Synchronous Generator，VSG)[4-7]控制技术，通过增加阻尼模块和惯量模块实现对同步发电机的机械特性和电磁特性的模拟，以增大系统惯性，使系统具有更好的频率稳定性[8-9]。文献[10-13]研究了如何优化设计惯性和阻尼参数以使其具有更好的控制性能。文献[14,21]提出了一种改进VSG控制方法，通过调整虚拟电抗，实现了更好的有功功率控制。文献[24]研究了一种应用VSG的控制策略实现母线电压平衡，并兼顾了功率双向流动特性。

传统微电网上层控制采用集中式，存在过于依赖中央控制器的问题。稀疏式通信网络的分布式控制方案中各个节点具有相等地位，可提高系统可靠性。文献[15-16]提出一种基于虚拟同步发电机的分布式协调控制方法，以降低稳态下系统母线电压和工作频率的误差。上述传统微电网控制策略一般侧重于按照分布式电源的容量比例分配功率，尚未全面考虑分布式电源在实时发电成本方面的差异，存在系统整体经济性偏低的不足。为了降低系统整体运行成本，文献[17]研究了基于改进经济下垂控制原理的系统策略，但考虑到线路阻抗的存在，难以实现较高精度的功率经济分配。文献[18-19]研究了基于分布式算法实现经济调度策略，但是依赖于主导节点的选取，尚未实现严格意义上的节点地位对等，间接削弱了整体系统可靠性。文献[20]提出一种通过改变下垂系数寻找最优经济运行点的方法，实现了自治直流微电网分布式经济下垂控制。文献[25-26]研究了一种多项式滤波法可加快分布式一致性经济分配算法的收敛速度。此外，上述控制策略有待从储能电池相关SOC状态参数角度出发，实现微电网多储能电池能量均衡优化和系统经济稳定运行。

在现有研究的基础上，针对孤岛微电网提出一种基于虚拟同步机技术和储能剩余电能状态(State of Charge, SOC)的分布式一致性经济控制策略。在底层一次控制中采用虚拟同步机技术，为系统提供惯性以及电压频率支持。针对系统上层控制，重点提出一种考虑一致性算法的微电网分布式信息交互模型及经济控制策略，通过少量节点间的信息交互，利用分布式一致性算法对VSG参数进行优化。在考虑各储能SOC状态平衡的基础上实现系统经济运行，并按照额定值分别优化频率和平均母线电压。最后通过搭建系统仿真模型，验证了文中相关理论研究的正确性及控制策略的效果。

1 虚拟同步机技术的原理

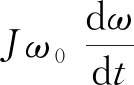
(1)

式中θ为VSG的转子角度；ω为VSG产生的转子角频率；ω0为额定角频率；J为VSG的虚拟转动惯量；D为阻尼系数；Pm和P为VSG输入机械功率和输出电功率。

Pm用下垂控制原理产生：

Pm=P0+kG(ω0-ω)

(2)

式中P0为额定有功功率；kG为发电机有功下垂系数。

将式(2)代入式(1)得：

(3)

VSG相关无功控制部分实现对同步发电机实际励磁调节功能的模拟，虚拟电动势E的控制方程为：

(4)

式中U0为额定电压；ΔE为模拟励磁调节器输出补偿电压；E为虚拟内电势；kq为无功补偿系数；Qm、Q为VSG无功功率参考值、输出无功功率值。

Qm由下垂控制原理得到：

Qm=kv(U0-U)+Q0

(5)

式中Q0为无功额定值；U为端口输出电压；kv为无功-电压下垂系数。

2 考虑储能SOC的微电网分布式一致性经济优化控制

图1所示为分布式一致性微电网经济优化控制的总体架构，各节点由设备、控制器和信息交互模块(Information Communication Module，ICM)三部分构成。底层的分布式电源设备构成物理层面的微电网系统，分布式电源的输出由控制层控制器控制。通信层构造稀疏的分布式通信网络，该网络中各节点地位均等，利用信息交互模块与少量其他节点进行信息交互。ICM利用分布式算法产生控制器优化所需信息指令，在线优化控制器参数，实现提高经济性、平衡系统内储能SOC及频率电压优化的综合控制目标。该策略不依赖于中心控制器，有利于提升系统可靠性。

图1 微电网分布式一致性经济优化控制总体架构

2.1 计及储能SOC的微电网发电成本模型

传统分布式电源比如燃料电池(Fuel Cell, FC)和微型燃气轮机(Micro-Turbine, MT)，其发电成本和边际成本用式(6)和式(7)建模[17]:

C(P)=αP2+βP+γ,P≤PDGmax

(6)

(7)

式中α、β、γ为成本系数；PDGmax为传统DG最大输出功率。

储能电池(Battery, BA)能够通过充放电实现功率的双向流动。SOC低表示电池剩余容量少，需充电；SOC高则电池剩余容量多，可放电。考虑储能SOC的电池发电成本和边际成本模型[22]如下：

C(P)=a+b(P+3PBmax(1-SOC))+c(P+3PBmax(1-SOC))2

(8)

(9)

-PBmax≤P≤PBmax

(10)

式中a、b、c为电池成本系数；电池的输出功率为正值代表放电，负值代表充电；PBmax为电池最大输出功率。

不同SOC条件下电池边际成本函数如图2所示。

图2 不同SOC条件下的储能电池边际成本函数

在相同输出功率情况下，SOC越低边际成本越高；在相同SOC情况下，输出功率越多边际成本越高。

与有功成本相比，无功成本所占比例相对较小[7]，文中重点研究有功功率成本相关的经济优化，建立如下考虑储能SOC的系统发电成本最优模型：

(11)

式中PD为系统中负荷功率。

系统运行在稳定状态下，各分布式电源的边际成本达到相同水平时，整体发电成本实现最小化[17]，即：

(12)

因此从边际成本一致的思路出发协调系统内功率分配，边际成本较高的分布式电源输出功率较低，可有效降低整体发电成本。对于储能电池，SOC低的电池输出功率少，减缓SOC的下降，反之SOC下降较快，从而在经济运行的同时实现系统内各储能电池SOC均衡。

2.2 基于一致性算法的分布式信息交互模型及经济控制策略

2.2.1 一致性算法的原理

分布式控制中节点利用信息交互模块与少量节点交互信息，通过一致性算法得到控制器优化所需指令。一致性算法如式(13)所示，令xi代表节点i的状态变量，将与节点i存在通信互联的节点定义为其邻居节点j，用集合Ni表示。

(13)

式中n为节点数，k=0，1，…是离散时间变量；xi[k]是节点i的状态经过第k次更新得到的值；xi[k+1]是节点i的状态在xi[k]和邻居j的状态xj[k]的基础上进行第k+1次迭代后所得更新的状态；dij为邻居j状态变量作用在节点i状态的权重，其大小与网络拓扑结构有关；dij的构造可采用基于邻居节点数的Metropolis方法[23]:

(14)

式中max(ni,nj)代表节点i对应邻居个数和邻居节点j对应邻居个数的最大值。

该构造方法不仅对网络结构具有适应性，并且收敛性良好，当各个节点的状态参数接近相等时，即系统整体实现了一致收敛，收敛于初始状态变量的平均值，即：

(15)

2.2.2 基于一致性算法的分布式信息交互模型

各节点ICM根据周期为Ts的同步采样时钟进行信息采集和交互。节点共需要交互三个状态量：边际成本IC信息、节点频率偏差δω和电压偏差δU。节点需采集本地的边际成本ICl、频率偏差δωl=ω0-ω及电压偏差δUl=U0-U信息。以节点i的边际成本信息处理过程为例，分布式信息交互模型如图3所示。

图3 基于一致性算法的分布式信息交互流程图

具体流程包括以下步骤：

(1)系统初始化，k=0，ICMi将采集到的信息存储，即ICi[k=0]=ICl，进而将ICi[k]发送给邻居节点j；

(2)ICMi接收节点j发送来的信息ICj[k]；利用所拥有的信息ICi[k]和ICj[k]进行一致性算法计算，得到更新状态ICi[k+1]，将k+1值赋给k，再向邻居节点发送更新的状态ICi[k]；

(3)循环重复步骤(2)进行更新迭代。

假设K次后各节点状态逐渐趋于一致，ICM得到一致时的状态即边际成本平均值ICave=ICi[K]。同理可得到角频率偏差均值δωave，电压偏差均值δUave。进而传统分布式电源和储能电池目标功率可表示为：

(16)

2.2.3 基于VSG的分层分布式一致性经济控制

所提基于VSG的微电网分层分布式一致性经济控制如图4所示，分布式电源通过逆变器及LC滤波器接入系统。

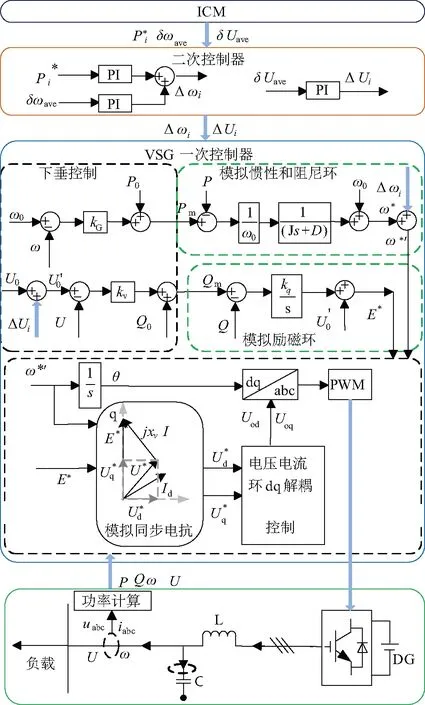
图4 基于VSG控制的微电网分布式经济控制框图

3 仿真分析

3.1 微电网仿真平台搭建

为了验证所提策略的有效性，建立了基于Matlab/Simulink仿真平台的微电网算例模型，图5所示为系统模型结构。模型中主要涵盖了燃料电池、微型燃气轮机和储能电池三类典型分布式电源，分布式电源通过逆变器接口接入交流母线，逆变器采用VSG和分布式一致性经济控制。表1中为系统相关电路基本参数及控制策略参数。

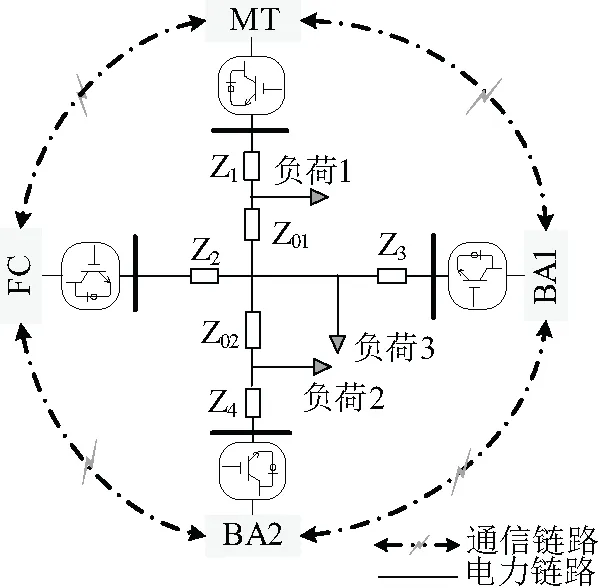
图5 微电网算例模型结构

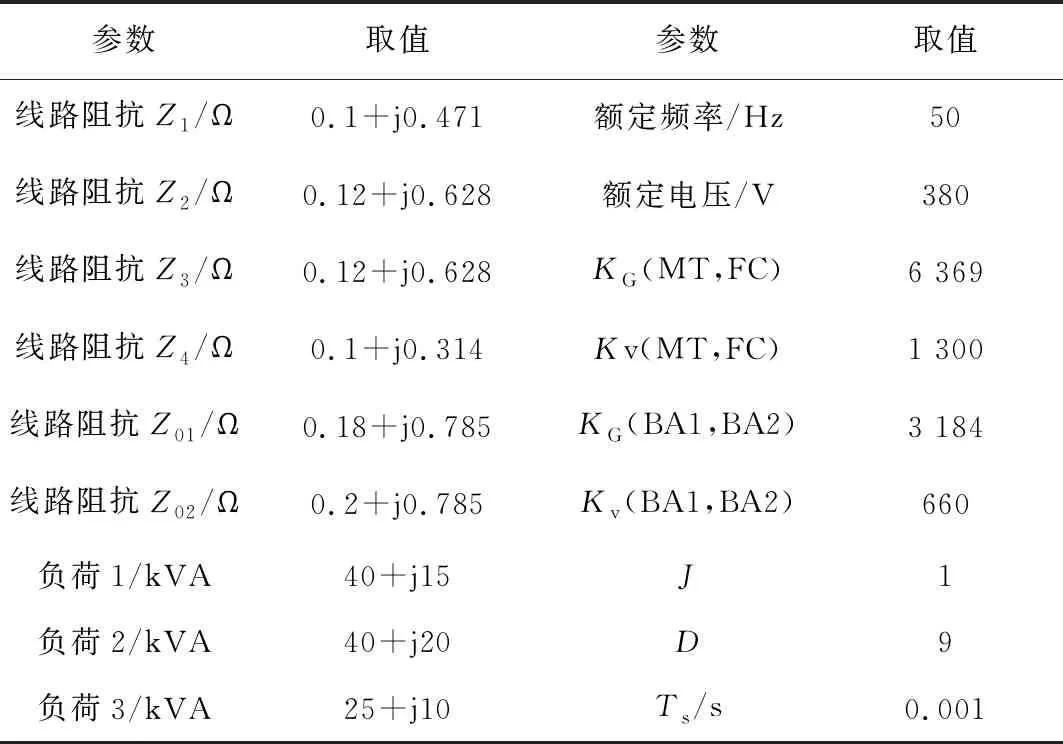
表1 微电网系统电路和控制参数

各节点间建立稀疏通信网络，根据式(14)计算各权值dij如式(17)所示。分布式电源的成本系数[17,20,23]如表2所示。

(17)

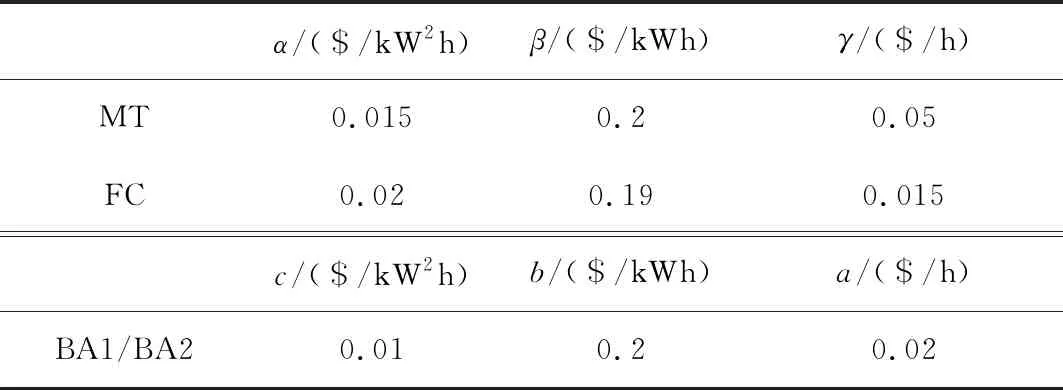
表2 DG和BA成本参数

3.2 分布式一致性经济控制策略效果分析

3.2.1 策略有效性及负荷扰动影响分析

系统中BA1和BA2初始SOC设为0.8，投入负荷1和负荷2。针对策略有效性及负荷扰动影响的具体仿真分析过程如下：

(1)在0.5 s之前系统仅在VSG一次控制下运行，未启动分布式二次经济控制策略。如图6所示，在VSG控制下实现系统稳定运行，但是频率和电压相比额定值具有明显的跌落，各分布式单元自动分配有功功率，未按照发电成本高低分配;

(2)在0.5 s时刻启动文中所述的分布式经济控制，节点利用ICM与其邻居节点进行信息交互及一致性信息处理，通过二次控制对VSG的控制参数进行优化，从而协调控制系统内各单元的输出功率及电压。如图6(a)和图6(b)所示，系统平均频率和平均母线电压在分布式控制作用下逐渐恢复至额定值；在图6(c)和图6(d)中，采用所提策略后，成本高的FC输出减少，各单元的边际成本逐渐在调节下趋于一致，从而使得系统整体发电成本降低;

(3)在1.5 s时刻继续投入负荷3，频率和电压出现短暂的暂态降落，但是经过分布式经济控制策略的调节，各单元重新分配功率，消纳新增加的负荷，平均频率和平均电压迅速稳定在额定值，边际成本再次趋于一致，上述仿真结果表明所述控制策略有效性不受新增负荷扰动影响。

图6 负荷变化情形下的系统运行情况

图7所示为各节点边际成本离散状态量的若干轮一致性迭代过程，ICM在时钟驱动下进行信息交互并利用一致性算法处理信息，随着迭代次数增加，各节点的边际成本状态可逐渐更新并收敛到一致的边际成本均值。各节点利用一致的边际成本均值，实现全局有功功率经济协调分配。收敛之后各节点再次采集实时本地边际成本，进行新一轮的一致性迭代过程。

图7 各节点边际成本一致性迭代过程

3.2.2 不同策略的发电成本对比

为了验证所提策略的经济性，将所提分布式经济控制策略与传统功率控制策略[15]进行对比。BA1和BA2初始SOC分别为0.8和0.9。如图8和表3所示，0.2 s前在一次控制下系统稳定运行，0.2 s启动不同的上层控制策略后，传统策略按照下垂系数的比例分配功率并进行电压、频率调节，MT和FC输出有功功率是储能电池的两倍，由于未全面考虑发电成本因素，导致在传统控制策略下运行的系统发电成本较高。提出的分布式一致性经济控制策略通过基于稀疏通信网络的信息交互，可按照边际成本一致的原则,协调分配各单元输出功率，成本高的分布式电源输出少，因此系统发电成本较低，所提策略相比传统策略可有效降低约8%的成本。在1 s时刻负荷3投入，重新消纳新增负荷后。如表3所示，随着负荷总量的增大，所提分布式经济控制策略更有利于降低发电成本。

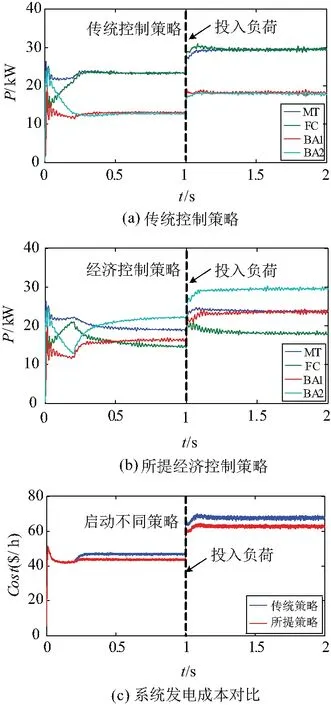
图8 不同策略的有功功率波形和发电成本对比

表3 不同策略下系统发电成本对比

3.2.3 平衡各储能电池SOC效果分析

为分析所提经济控制策略平衡利用多储能电池的效果，系统以两台储能电池为例，BA1和BA2初始SOC分别设为1和0.9。储能电池SOC在所提控制策略下的均衡效果如图9所示，由于储能电池的发电成本模型中考虑了SOC因素，具有低SOC特征的电池发电成本较高，在分布式功率经济分配中，BA2输出功率低于BA1，SOC下降速率相对较慢；反之BA1输出功率越大，SOC下降越快，逐渐均衡系统各储能剩余容量，实现储能电池的协同优化利用。

图9 储能电池SOC在所提控制策略下的均衡效果

4 结束语

为了缓解传统微电网集中式控制对于中心控制器的过度依赖，同时考虑系统运行经济性，提出了基于虚拟同步机技术的微电网分布式一致性经济控制策略，得到结论如下：

(1)一次控制采用VSG以增大系统惯性，并为系统提供电压和频率支撑。在所提的微电网分布式一致性经济控制策略中，考虑储能SOC建立系统发电成本模型，采用基于一致性算法的分布式信息交互模块获取控制器所需信息，进而在二次控制中利用以上信息实现VSG控制的参数优化；

(2)仿真结果表明该控制策略有助于提高系统的经济性，并根据额定值实现对系统工作频率和各母线平均电压的调节，平衡各储能单元可用容量；

(3)所研究的策略基于稀疏通信网络，不依赖于中心控制器，可靠性较高，且所需信息量少，无需获取线路阻抗和负荷信息。并且相关通信网络的构建与电力网络结构无耦合关系，不受电力系统拓扑变化的影响，为提高系统灵活性和适应性提供了新思路。