基于时域能量与自适应奇异值阈值的改进局放信号去噪方法

2022-10-11何青霜谢敏周凯

电测与仪表 2022年10期

何青霜，谢敏，周凯

(1.四川师范大学计算机科学学院，成都 610101； 2.国网无锡供电公司，江苏无锡 214000；3.四川大学电气工程学院，成都 610065)

0 引言

交联聚乙烯(Crosslinked Polyethylene，XLPE)电力电缆因其可靠的电气绝缘和机械性能在城市输配电网络中应用广泛[1-2]。然而在实际运行中，由于受到电、热、机械等多重应力及运行环境的影响，电缆开始出现不同程度的绝缘老化问题，从而对电网的安全稳定运行产生一定的影响。

为了保证电缆的供电可靠性，需要定期对电缆的绝缘状态进行检测。其中，局部放电(Partial Discharge，PD)(简称局放)检测是判断电缆绝缘状态的有效手段[3]。然而，受现场复杂电磁环境的影响，实际测量得到的局放信号容易受到各种噪声的影响，如由电气设备热噪声引起的白噪声[4-5]、通信系统引起的周期性窄带干扰及电力电子设备产生的脉冲型干扰等[6-7]，从而对局放检测系统的检测灵敏度产生一定的影响。为了精确地对局放信号进行分析，首先需要对实际测量得到的局放信号中的噪声进行抑制。考虑到实际中白噪声最为常见，文中将针对白噪声的抑制问题进行研究。

为了实现局放信号白噪声的抑制，近年来国内外学者也进行了大量的研究工作，主要包括小波变换法[8-9]、经验模态分解[10](Empirical Mode Decomposition，EMD)法、奇异值分解[11-12](Singular Value Decomposition，SVD)法等。其中，小波变换法由于具有较好的多尺度分析能力，因此在实际中应用最为广泛[13-14]。但其也存在小波基、分解层数及阈值函数难以选取等问题[15]，且参数的选取结果均会对去噪产生一定的影响。EMD虽能自适应地对信号进行分解，但其也存在端点效应、模态混叠及阈值函数难以确定等不足[16]。相比于小波变换法与EMD法，SVD由于仅需对奇异值阈值进行确定，因此也开始得到一定的应用。不同于传统SVD去噪方法，文献[17-18]提出了一种基于短时奇异值分解(Short-time Singular Balue Decomposition，STSVD)的局放信号白噪声抑制方法，有效解决了传统SVD去噪后残余噪声较大及信号细节丢失严重的问题，但由于奇异值阈值选取需要受到人为因素的影响，因此在实际应用中受到一定的限制。同时需要说明的是，由于传统STSVD[18]需要对整个局放序列进行处理，因此其也存在计算速率较慢的问题。

文中在已有研究的基础上，针对传统STSVD存在的奇异值阈值难以确定及计算效率较慢的不足，提出了一种基于时域能量与自适应奇异值阈值的局放信号白噪声抑制方法。首先利用时域能量法对局放序列中的局放脉冲位置进行标定，然后利用自适应奇异值阈值策略对STSVD中的奇异值阈值进行确定，从而实现局放信号白噪声的抑制。仿真和实测去噪结果表明，该方法可有效去除局放信号中存在的白噪声，且相比于传统STSVD可显著提高计算速率，具有良好的应用前景。

1 基本原理

1.1 短时奇异值分解

SVD是线性代数中一种有效的信号分析方法。对于长为N的局放序列x= [x1,x2, …,xN]，SVD去噪主要包含以下4个步骤：

(1)给定矩阵行数L，构建L×K的轨迹矩阵X：

(1)

式中K=N-L+1；L通常可在N/20 ～N/2中进行选取，文中取L=N/3。

(2)利用SVD对轨迹矩阵X进行处理：

(2)

式中R= Rank(X) ≤L；(·)T为转置；矩阵U、V分别为正交矩阵，ur、vr为对应的左右奇异向量；Σ为L×K的对角矩阵，其对角元素{σr}为矩阵X的奇异值，且按降序排列。

(3)确定合适的奇异值阈值σth，并记矩阵X奇异值中大于σth的奇异值个数为M，利用下式进行去噪处理：

(3)

(4)对式(3)得到的去噪矩阵利用对角平均的方式进行去噪后局放序列的重构：

(4)

通过步骤(1)～步骤(4)即可实现局放信号噪声的有效抑制。然而在研究中发现，当局放序列较长时，由于序列的复杂度较高，无法利用较少的奇异值(M较小)对信号进行重构，因此去噪后信号细节丢失且存在较多的残余噪声。为此，文献[17]提出利用STSVD对局放信号的白噪声进行抑制。STSVD去噪方法主要步骤如下：

(1)根据局放脉冲波形设置合适的滑动数据窗长度T；

(2)根据设置的窗长T对含噪局放序列进行分段截取，截取的相邻含噪局放片段重复数据点数为T-1；

(3)对含噪局放片段进行奇异值分解；

(4)根据设定的奇异值阈值对含噪局放片段进行噪声抑制；

(5)利用式(4)重构去噪后的局放片段，然后相邻局放片段中重复位置的数据点利用求平均值方式进行处理，得到最终去噪后的局放序列。

相比于传统SVD去噪方法，STSVD由于利用滑动数据窗截取了含噪局放信号片段，从而大大减小了待分析信号的复杂度，因此相比于传统SVD去噪方法去噪效果更好。

1.2 自适应奇异值阈值

由前述SVD及STSVD去噪原理可知，当奇异值阈值σth选择过大时，大量有用信号丢失，去噪后波形失真严重；σth选择过小时，大量噪声又得到保留，去噪后信号残余噪声较大。因此，为了得到较好的去噪效果，需要选择合适的奇异值阈值。

为了自适应地选取奇异值阈值σth，文献[11]利用奇异值序列标准差实现了阈值的自动选取(Adaptive Singular Value Decomposition，ASVD)，但该策略无法处理仅含噪声的序列(STSVD截取的信号片段)，且当信噪比(Signal to Noise Ratio，SNR)较低时阈值的选取受到人为因素影响较大。文献[17-18]提取的阈值选取策略虽能处理仅含噪声的序列，但也存在实现过程复杂及人为因素影响较大等不足。为此，本文结合信号源数目的估计方法[19]，通过噪声概率密度结合信息论知识，首次引入下式所示自适应奇异值阈值确定方法(获得重构奇异值个数M)：

(5)

M=min[ζ(k)],k=0,1,…,R-1

(6)

式(5)中,当对整个局放序列进行SVD处理时，N为局放序列的长度；当利用STSVD进行处理时，N为滑动数据窗长度T；R为对应序列的奇异值个数。由式(5)、式(6)可知，重构奇异值个数M完全由奇异值{σr}自适应确定，不受人为因素影响。

为了验证式(5)、式(6)所示自适应奇异值阈值的有效性与准确性，模拟产生幅值相位均为10 mV、0°，频率分别为1 MHz、3.3 MHz、5 MHz、8.1 MHz及10 MHz的5个正弦信号(叠加)，采样频率设置为200 MS/s，采样点数为2 000。利用上述奇异值阈值自适应确定方法对仿真信号的源数目进行估计(确定M，准确值为源数目的2倍)，添加噪声为高斯白噪声，并将估计结果与ASVD及文献[18]方法(记为传统STSVD)的估计结果进行比较，得到不同SNR(能量计算方式)下的估计结果如图1所示。需要说明的是，为了显示不同方法的整体估计性能，M取仿真100次的平均值。

图1 不同方法信号源数目估计结果

由图1结果可知，当SNR较高时，ASVD及文中的自适应奇异值阈值策略均能准确地对信号源数目进行估计；但当SNR较低时(-5 dB)，ASVD的估计结果将存在较大的偏差，相比而言，本文的估计策略估计效果更好。对于传统STSVD的估计策略，其存在过估计现象，即M估计结果偏大。

1.3 改进的去噪算法

进一步分析传统STSVD去噪方法可知，由于传统STSVD需要沿着整个局放序列进行信号截取及SVD处理，因此当序列较长时，计算所需的时间也较长。考虑到实际测量得到的局放脉冲仅在部分区域存在(其他区域为白噪声)，文中首先利用时域能量[20]对局放脉冲区域进行标定(白噪声时域能量服从自由度为T的χ2分布，可参见文献[20])，然后仅对标定区域利用STSVD进行去噪处理，从而有效提高STSVD的计算速率。信号时域能量的计算方法可参见文献[20]，此处不再累述。

由上述可知，文中所提基于时域能量与自适应奇异值分解的改进局放信号去噪方法具体步骤如下：

(1)利用下式所示时域能量计算方法对局放序列的时域能量ET(k)进行计算[20]：

(7)

式中T取为奇数；k为求取的时域能量点，k= (T+1)/2, …,N-(T-1)/2；η为白噪声的标准差，可由第一层小波系数估计获得[18]；

(2)记录大于时域能量阈值(概率设置为0.995，阈值可查表获得)的局放脉冲所在区域；

(3)对记录的局放脉冲所在位置利用STSVD进行左右两侧滑动去噪，直至计算得到的重构奇异值个数M为0。奇异值阈值选择策略利用式(5)、式(6)进行确定；

需要说明的是，当信号含有直流偏置(低频干扰)时，可首先利用数字低通滤波器对直流偏置(低频干扰)进行滤除。

2 仿真局放信号去噪

由局放信号实测结果可知[21]，实际测量得到的局放脉冲通常可利用双指数衰减函数(s1)和双指数衰减振荡函数(s2)进行模拟：

s1(t)=A(e-1.3t/τ-e-2.2t/τ)

(8)

s2(t)=A(e-1.3t/τ-e-2.2t/τ)×sin(2πfct)

(9)

式中A为幅值；τ为衰减系数；fc为振荡频率。分别取A= 10 mV、τ= 0.5 μs、fc= 2 MHz。仿真采样频率为50 MS/s，采样点数为2 000。仿真得到无噪局放信号如图2(a)所示。图2(b)为添加高斯白噪声SNR=0 dB时的含噪局放信号。

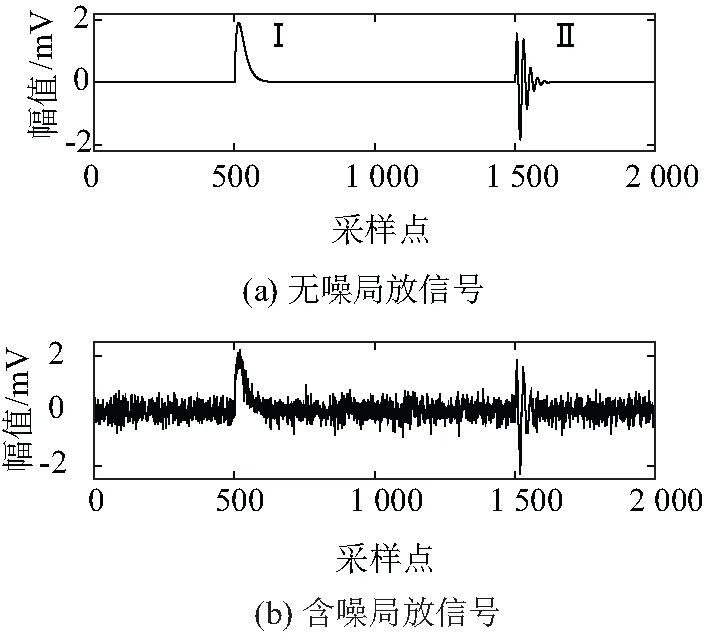
图2 仿真局放信号

利用文中所提去噪方法对图2(b)所示含噪局放信号进行去噪处理(窗长取81)，得到去噪结果如图3(a)所示。为便于比较，图3(b)～(d)分别给出了ASVD、传统STSVD[18]及MATLAB小波去噪工具箱(db8小波，分解8层)的去噪结果。为了定量评估去噪效果，利用式(10)、式(11)所示波形相似系数[22](Normalized Correlation Coefficient，NCC)、均方根误差(Root Mean Square Error，RMSE)对去噪结果进行评估，计算结果如表1所示(采样点250～750及1 250～1 750区域)。

(10)

(11)

式中x1、x2分别为不含噪局放信号和去噪后局放信号。NCC用于评价去噪前后信号的相似程度，计算结果在[-1,1]之间，越接近1表明去噪后波形与原始波形越相似，去噪结果越好；RMSE用于评价去噪前后信号的均方误差，值越小表明去噪效果越好。

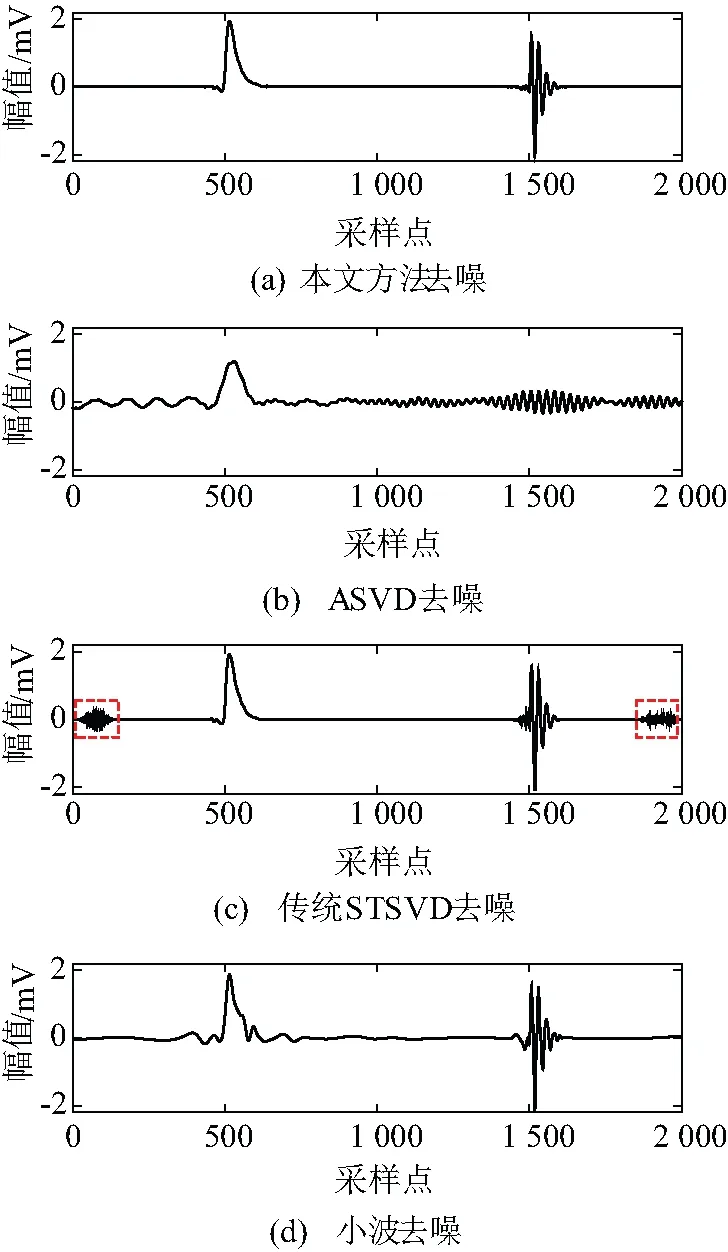
图3 仿真局放信号去噪结果评估

由图3及表1去噪结果可知，相比于传统STSVD、ASVD及小波去噪结果，文中所提去噪方法去噪效果最好，去噪后波形与原始波形相似度更高、误差更小。但需要指出的是，虽然传统STSVD也能取得很好的去噪效果，但由于奇异值阈值估计时存在过估计现象(图1)，因此去噪后波形的部分区域仍存在较明显的毛刺点(图3(c)标识区域)。与此同时，由于文中所提去噪方法仅需对局放脉冲区域进行去噪处理，因此运算速率更快，图2所示情况下文中方法计算速率约为传统STSVD的5倍。

为了说明文中所提方法相对于传统STSVD方法在计算速率方面的提升，改变图2的采样时间，保持其他参数及局放脉冲波形个数不变，得到不同采样时间及不同窗口长度下(窗口长度分别为101、81及51)的执行效率如图4所示。由图4结果可知，由于传统STSVD需要对整个局放序列进行去噪处理，因此当数据量较大时其计算效率开始降低。相比而言，文中所提去噪方法计算效率仅与局放脉冲个数相关，去噪速率受局放序列长度影响较小。

3 实测局放信号去噪

为了验证所提去噪方法对实测局放信号去噪的有效性，在实验室搭建了图5所示35 kV XLPE电缆油终端局放测试平台。图中，无局放变压器最大电压为150 kV，R为保护电阻，示波器最大采样率5 GS/s，高频电流传感器(High Frequency Current Transformer，HFCT)最大灵敏度为9.14 mV/mA(25 MHz)，带通滤波器带宽为1.2 MHz～80 MHz。人工模拟制作刀痕缺陷(长100 mm、宽0.2 mm、深1 mm)，测试得到局放信号如图6(a)所示，其中采样率为50 MS/s。图6(b)～图(d)分别为本文方法、传统STSVD(滑动窗口长度51)及MATLAB小波去噪工具箱(db8小波，分解8层)的去噪结果(由于局放序列较长时ASVD去噪效果较差，此处未进行考虑)。

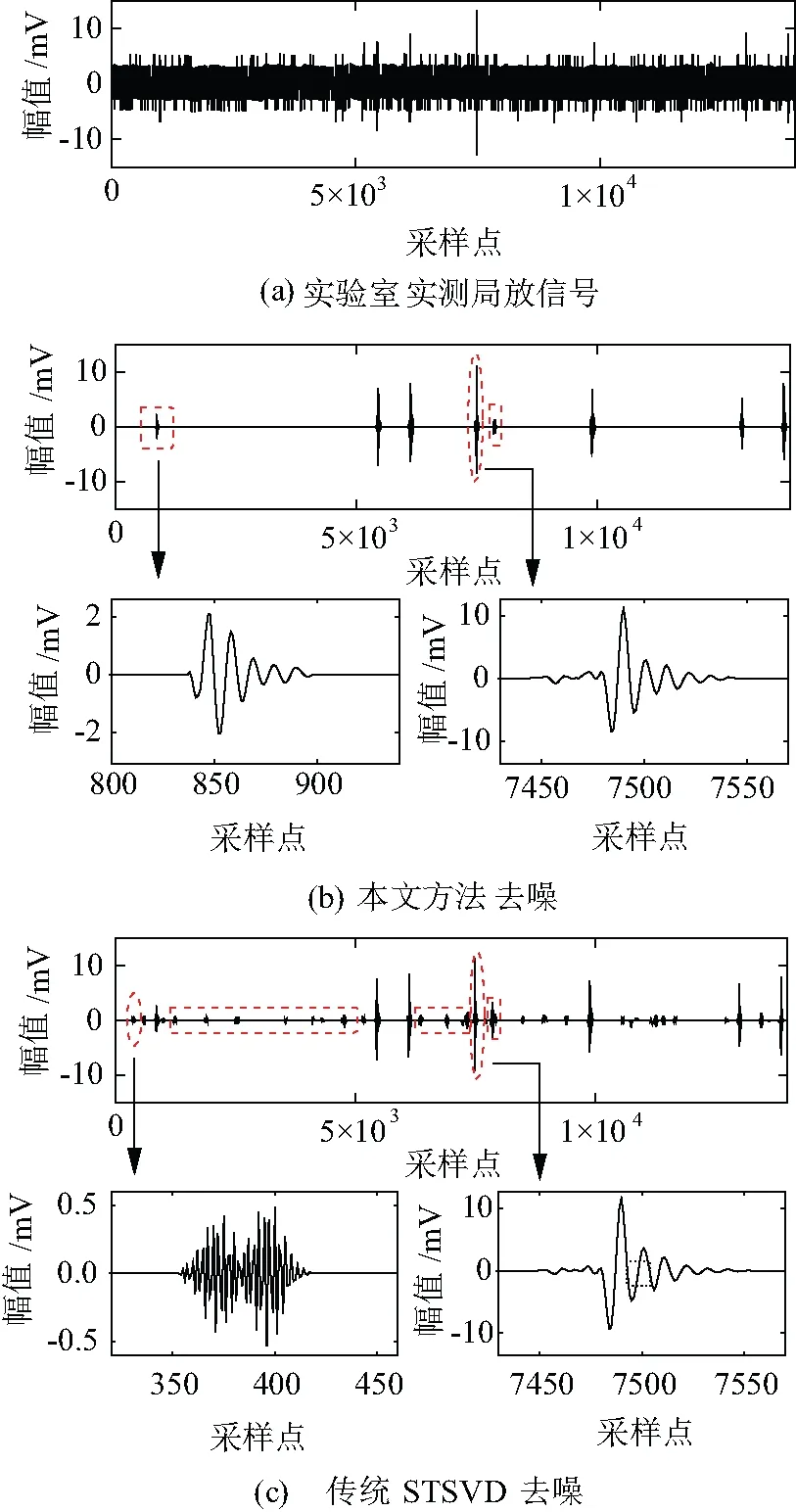
图6 实验室实测局放信号去噪结果

分析图6(b)、图6(c)可知，相比于文中所提去噪方法，由于传统STSVD采用的奇异值阈值估计方法存在过估计现象(见图1)，因此去噪后结果存在较多的毛刺干扰(图6(c)中标识区域)；与此同时，文中方法对数据进行处理时计算时间为0.47 s，而传统STSVD计算时间为5.68 s，由此说明本文方法计算速率远优于传统STSVD计算方法。对于小波去噪，去噪后则存在部分局放脉冲丢失现象(图6(b)中标识区域的波形，局部放大后人为判断结果)。

进一步地，为了验证文中方法对现场实测局放信号的去噪效果，利用图5所示局放采集装置(HFCT与示波器)对现场某10 kV XLPE电缆进行局放测试，测试现场如图7所示。

图7 现场局放测试

采样率设置为1 GS/s，得到测试局放波形如图8(a)所示。分别利用文中方法、ASVD、传统STSVD(滑动窗口长度121)及MATLAB小波去噪工具箱(db8小波，分解8层)进行去噪处理，得到去噪结果如图8(b)～图8(e)所示。

图8 现场实测含噪局放信号去噪结果

由于无法获得不含噪声的局放信号，因此无法利用上述NCC和RMSE对去噪结果进行定量评估，为此，文中引入文献[6]中的噪声抑制比rNNR和去噪后信噪比rSNR对去噪结果进行评估，如式(12)、式(13)所示。

rNNR=20(lgη1-lgη2)

(12)

(13)

式中η1和η2分别为去噪前信号x和去噪后信号y的标准差。

计算结果如表2所示。

表2 现场实测局放信号去噪评估

由图8去噪结果可知，对于幅值较大的局放脉冲，4种方法均能有效地进行去噪处理。但对于较小的局放脉冲，仅传统STSVD及文中方法能够较好地进行识别(相比于右侧幅值较大的局放脉冲)，但传统STSVD去噪后存在较多的毛刺干扰(图8(d)中标识区域)，且其计算时间约为文中方法的5倍。进一步分析表2去噪结果可知，相比于ASVD、传统STSVD及小波去噪方法，文中所提去噪方法去噪后信噪比最高，且其噪声抑制比高于传统STSVD去噪方法。对于ASVD和小波去噪，由于去噪后信号细节丢失严重(去噪后信号标准差较小)，因此计算得到的噪声抑制比较高。