计算全息图的快速生成技术

王迪 李赵松 黄倩 王琼华

（北京航空航天大学仪器科学与光电工程学院，北京 100191）

1 引言

现实世界是3D 世界，而传统的2D 显示设备只能提供平面图像显示，无法使观看者获得身临其境的观看体验。为了使人们更真实地认识客观世界，显示技术从2D 向3D 发展已成为了一种趋势。在3D 显示技术中，全息3D 显示技术基于物理光学原理，利用光的衍射重建3D 物体的波前信息，从而提供人眼所需要的全部深度信息［1］，人眼在观看3D 物体重建像时不会产生立体观看视疲劳。因此，全息3D显示被视为3D显示未来发展的重要方向之一。

如何实现全息图的快速计算是全息3D显示的关键问题之一。当记录复杂3D 物体时，全息图的计算量急剧增加，需要很长的计算时间才能生成全息图。为了克服这一问题，许多提高全息图生成速度的算法和加快计算速度的硬件设备被开发了出来［2-6］。本文将针对计算全息图的快速生成技术进行介绍。首先围绕标量衍射理论分析全息3D 显示的基本原理，接着基于3D物体的数学描述方式对计算全息图的快速生成方法进行分类介绍，并概述了利用硬件加速法和深度学习法加快全息图计算速度的典型工作，最后对计算全息图的快速生成方法进行总结。

2 全息3D显示的原理

计算3D 物体的全息图主要在于计算物光波从3D物体到全息面的衍射传播过程，该过程主要是基于标量衍射理论来进行近似计算。波前上的任意一点都可看作是子波源，它们都能产生球面子波，后一时刻的波前位置是所有子波波前的包络面［7］。当一束光经过孔径平面Σ 发生了菲涅尔衍射，在孔径后任一点P处观察时，孔径平面上也存在一点P1作为子波源向后发射球面子波。设P1到P的直线距离为r0，传播方向与方向法线夹角为θ，根据惠更斯-菲涅耳原理，观察点P处的光场U（P）满足：

其中，k是波数，λ是光的波长，i代表虚数，ds是点P1的面积，U（P1）是点P1的光场分布。

如图1所示，考虑3D 物体上一个点到全息面的衍射过程［2，7］。记位于物平面（m，n）内有一点Q1，全息面（x，y）上有一点Q0，两点间的直线距离为r，传播光线与光轴z的夹角为α，物平面到全息面的距离为s，由几何关系可以求得cosα=s/r。根据公式（1）可以获得点Q0处的光场分布U（Q0）为：

图1 物点的标量衍射示意图Fig.1 Schematic diagram of the scalar diffraction of the object point

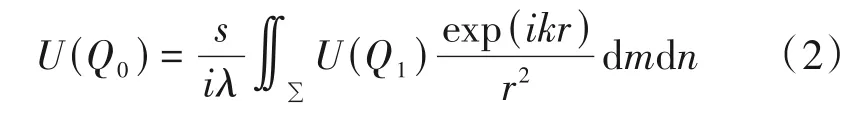
其中，U（Q1）表示物点Q1处的光场分布。

通过傍轴近似，公式（2）可简化为：

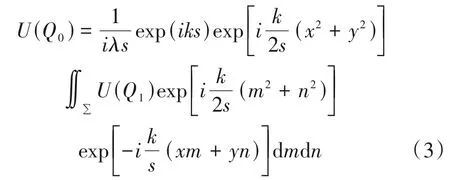
若采用菲涅尔衍射来计算3D 物体的全息图，则需要对每一个物点都采用菲涅尔衍射来计算与该物点对应的全息面上的复振幅分布，最后将物点叠加以获得3D 物体的全息图。这样的复振幅分布表示为：

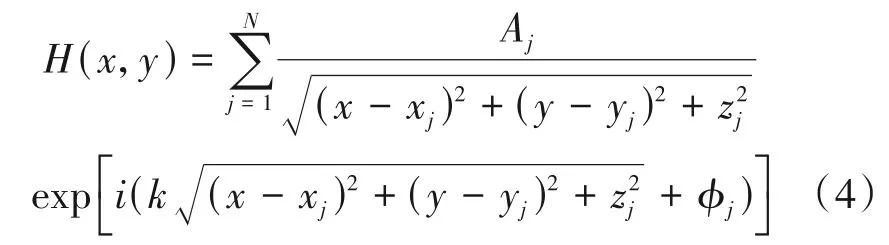
其中，H（x，y）表示全息面（x，y）上的复振幅分布，Aj表示第j个点光源（xj，yj，zj）的振幅信息，φj表示与第j个点光源对应的随机相位。假设3D 物体上有N个点光源，全息图的分辨率为a×b，那么公式（4）的运算量为N×a×b次，且每次计算都涉及到多次乘法运算及积分运算等，计算速度将变得非常慢。要做到实时动态的全息3D显示，计算速度问题需得到有效解决。

3 计算全息图的快速生成方法

3D物体的数学描述方法具有不同的表达形式，如图2所示。根据3D 物体的几何信息，将其离散表示为一系列的点光源，即为点元描述；根据3D 物体的表面特征，利用一系列的三角形网格或多边形网格来描述3D 物体的表面信息，即为面元描述；根据3D物体的深度信息，将其离散为一系列平行于全息面的2D 切面，即为分层描述。依据不同的描述方法，计算全息图的生成方法可分为点元法、面元法和分层法三类［1］。此外，硬件加速法和深度学习法也在全息图的快速计算中起着重要的作用，接下来将分别进行介绍。

图2 3D物体的数学描述方法Fig.2 Mathematical description method of the 3D object

3.1 点元法

点元法的基本思想是利用3D 空间分布的一系列离散点光源来描述3D 物体，经典的基于点元法的快速计算方法有查表法（Look-up table，LUT）和波前记录平面法（Wavefront-recording plane，WRP）。美国麻省理工学院的研究人员提出了LUT 法来提高离轴透射全息图的计算速度［2］。在该方法中，与3D 物体的每个点元相对应的所有条纹图案都被预先计算并存储在查找表中。虽然条纹的存储需要占用较大的储存空间，但全息图的计算速度会有一个数量级的提升。为了减少查找表占用的储存空间，韩国光云大学的研究人员提出了新型查表法（Novel-LUT，N-LUT）［8］，如图3 所示。3D 物体被描述为空间中离散的点元，处于同一深度平面的点为一组，然后仅预计算和存储每个深度平面上位于中心点的主条纹图案（Principal fringe pattern，PFP），以此减少了生成全息图所需的条纹图案的计算量，计算速度相比LUT法提升了近744倍。

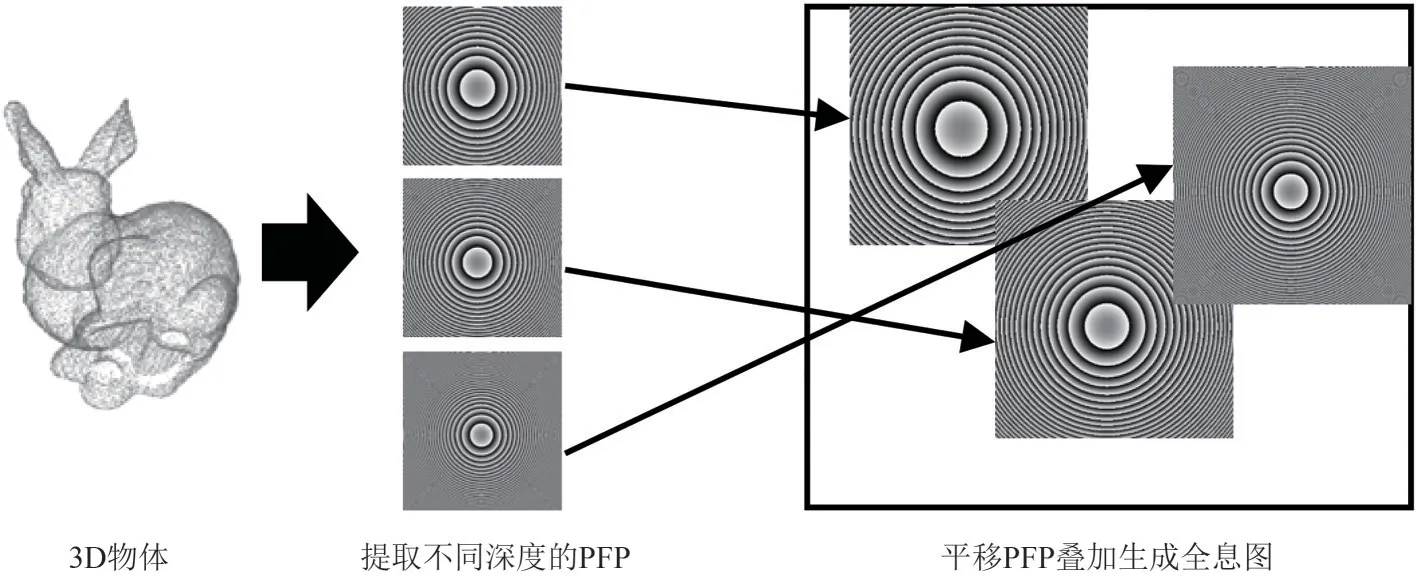
图3 N-LUT的流程图Fig.3 Flow chart of the N-LUT

新加坡国立大学的研究人员提出了一种分别使用水平和垂直方向的拆分查找表法（Split-LUT，S-LUT）［9］，降低了待计算的查找表的存储空间，S-LUT法的计算速度相比传统的LUT法提升了大约700 倍，相比传统的光线追踪方法也提升了大约100 倍。同时，由于S-LUT 法在图形处理单元（Graphics processing unit，GPU）上的内存使用量远低于LUT 法，这使得复杂3D 对象的全息图计算速度更快。韩国光云大学的研究人员对N-LUT 法进行了改进［10］，他们首先用基线PFP 来计算3D 视频的2D 全息图，然后用2D 全息图与深度补偿PFP 的乘积来计算3D 视频的3D 全息图，最后采用运动补偿将PFP 的存储容量从N-LUT 法的兆字节数量级降低到千字节数量级。该方法的计算速度相比N-LUT 法提高了30%。由于N-LUT 法需要计算的PFP 的数量与3D 物体的深度层数成正比关系，当3D物体的深度层数增加时，存储量大幅上升。为了解决这一问题，北京理工大学的研究人员提出一种与深度层数无关的压缩查表法（Compressed-LUT，C-LUT）［11］，通过预先计算并存储2D 切片平面上点的水平和垂直光调制因子，大大节约了存储空间。虽然C-LUT 法相比LUT 法计算速度得到显著提高，但预先计算的PFP 依旧占据大量内存。为了解决查找表的高存储空间需求，日本千叶大学的研究人员提出使用WRP 法来快速计算全息图［12］，如图4（a）所示。首先在波前记录平面上记录3D 物体发射的球面波，然后基于快速傅里叶变换，通过从波前记录平面到全息面的衍射计算来降低计算复杂度。在此基础上，该团队利用LUT 法来记录3D物体到波前记录平面的PFP，然后使用GPU 来加速完成波前记录平面的PFP 到全息面的衍射计算［13］，最终全息图的计算速度相比传统的WRP 法提高了80倍，实验效果如图4（b）所示。北京航空航天大学的研究人员通过分析3D 物体的大小、每个点的位置、空间光调制器的参数和重建距离之间的关系计算出再现像的有效视区，进而计算出各物点在全息面上的衍射面积大小，减小了存储的数据量。当物点数为600×600 时，计算速度比传统的N-LUT 算法提高了51%以上［14］。目前点元法的计算速度问题已得到有效解决，如何在提高计算速度的基础上，提高全息图的再现质量仍是点元法需要关注的问题。

图4 WRP法的方法示意图和实验效果图Fig.4 Schematic diagram and experimental result of the WRP method

3.2 面元法

基于点元法计算全息图的点元数量常高达数百万，而使用面元法可以将点元数量减少两到三个数量级。目前，计算机图形学已经建立起一套基于三角形网格法的离散、建模和计算方法，因此面元法可以借助计算机图形学计算3D 物体的全息图。根据采样方法的不同，面元法分为传统面元法和解析面元法。

传统面元法需要对每个面元的频域和空域都进行傅里叶变换运算。日本关西大学和德国耶拿大学的研究人员基于平面波的角谱和频域的坐标旋转，通过两次快速傅里叶变换和一次频谱插值，实现了非平行于全息面的孔径衍射波的复振幅计算［3］。北京理工大学的研究人员为了解决传统面元法在生成全息图的过程中存在大量数值计算的问题，提出了一种基于二维傅里叶分析的快速多边形计算方法［15］。该方法的实验效果如图5（a）所示。由于该方法不需要对每个多边形表面进行快速傅里叶变换和额外的扩散计算，因此可以节省计算时间，相比传统面元法计算时间缩短了25%。

爱尔兰国立大学的研究人员提出了解析面元法［16］，与传统面元法相比，解析面元法对于多面元的3D 物体也只需使用一次傅里叶变换，计算速度得到了快速提高。但是解析面元法的计算复杂度取决于全息图的分辨率和3D 物体的面元数量，复杂的3D 物体将影响解析面元法的计算速度。北京理工大学的研究人员提出了一种改进的基于全解析多边形的方法［17］，他们利用原三角形和任意三角形的顶点向量和伪逆矩阵，构造了表示两个三角形空间关系的仿射变换矩阵。该方法避免了每个多边形面元都要参与FFT 计算，相比传统的解析面元法，还省去了低阶的相关角度计算，计算速度提高了90%，实验效果如图5（b）所示。昆明理工大学的研究人员则将空间域的旋转和二维的仿射变换由旋转矩阵和二维仿射矩阵来表示，比传统的解析面元法计算速度提高了1倍［18］。从传统面元法和解析面元法的实验效果来看，虽然全息图的计算速度得到了提升，但是大量的矩阵变换和空间映射却带来了全息图重建质量的下降，如何在保证全息图计算速度得到提高的同时不对3D 物体信息造成损失仍是面元法需要解决的问题。

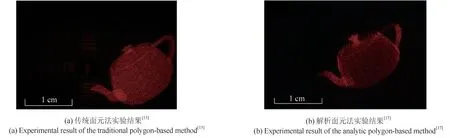
图5 面元法的实验效果Fig.5 Experimental results of the polygon-based method

3.3 分层法

为了进一步简化计算，研究者们提出了计算复杂度更低、数据量更少的分层法。分层法的基本思想是将3D物体切分为一系列平行于全息面的2D切片，这些切片包含了3D 物体各个深度的振幅信息，可以使用面与面之间的传播算法如角谱法、快速傅里叶法等来实现快速计算。清华大学的研究人员提出了基于角谱的分层法［4］，实验效果如图6（a）所示。每层图像的振幅信息在与随机相位叠加后进行角谱传播。在不考虑傍轴近似的情况下，将每层图像在全息面的频谱分布叠加就能获得3D 物体在全息面的频谱分布，最后使用逆傅里叶变换获得全息图的复振幅分布。该方法避免了点元法和面元法的巨大计算量，能准确预测3D 物体的整个衍射场，在分层数量一定的前提下，计算量与3D 物体的复杂度无关。与传统的分层法相比，基于角谱的分层法能在不降低图像分辨率的前提下有效地减少全息图的计算量。

图6 分层法的实验效果Fig.6 Experimental results of the layer-based method

为了提高分层法的计算速度，剑桥大学的研究人员提出了基于快速两步分层算法和亚稀疏二维快速傅里叶变换算法［19］。考虑到分层法中不同层之间的遮挡效应，每个层的图像包含像素值为零的大图像区域。利用这一特性，快速两步分层算法只计算了每一层的非零图像区域。此外，亚稀疏二维快速傅里叶变换算法只计算了分层图像的非零像素的行和列，降低了傅里叶变换的计算量。与传统的分层法相比，这两种方法与分层法的结合使计算速度提高了至少3 倍。由于3D 物体的信息在衍射计算中分布到了整个全息图平面，亚稀疏二维快速傅里叶变换在减小计算区域同时可能会导致3D 物体的信息丢失，这将引起重建图像的质量下降。日本千叶大学的研究人员通过使用实值傅里叶变换和哈特莱变换作为实线性变换来减少耗时的复数运算，并将由实线性变换产生的全息图通过半波带片法和数字化单边带法转换为了纯相位全息图。该方法相比传统的分层法计算速度提高了3倍［20］，实验效果如图6（b）所示。

目前，分层法的计算速度已得到显著的提高，许多分层法中存在的问题如遮挡效应，缺乏深度线索等得到了解决，但是重建图像的实时渲染和重建图像质量的提高仍然是分层法需要进一步解决的问题。

3.4 硬件加速法

除了从算法的角度来提升计算全息图的生成速度以外，硬件平台的算力提升对于快速计算也很关键。近年来，随着硬件运算速度的快速提升，越来越多的研究人员利用高性能硬件设备来完成全息图的计算。传统的全息图算法是在中央处理器（Central processing unit，CPU）上运行的，尽管目前CPU 的处理能力有所提高，但对于实时应用来说还远远不够。加速硬件平台，通常包括GPU 和可编程门阵列（Field programmable gate array，FPGA）等，能够配合算法快速计算全息图。

CPU 是现代计算机的核心组件，使用CPU 的最大优点是开发时间短，几乎所有可以在其他硬件加速器平台上找到的软件包都具有相同或等效的工具包可以在CPU 上使用，而且CPU 对双精度浮点运算的支持往往更好。但是，CPU 无法实现输入数据完全的并行运算。与CPU 不同的是，GPU 在硬件结构上体现出了并行性，同时，GPU 可以使用高级编程语言进行编程，这使得开发和调试过程比其他平台更快、更容易。麻省理工学院的研究者基于GPU提出了一种允许进行若干计算简化的全息算法。该算法在2 s 内可以计算出一个6 MB 的全息图，比传统的计算机快100倍［21］。日本千叶大学的研究者使用HLSL和DirectX API实现了对基于GPU的线性全息图算法的加速，将计算速度提升了47倍［5］。此外，FPGA 作为一种高度可配置的集成电路，能够在制造后由设计者重新编程。近年来，使用基于FPGA架构的集成芯片来提高全息图计算速度的方法也被提出［22］。如图7所示，基于FPGA的全息算法可以迁移到非常大规模的集成芯片上，且不需要进行大规模的修改［23］。大规模集成的可编程FPGA 的出现为实现全息图的快速生成提供了硬件支撑，但FPGA的设计难度大、加工成本高，目前仍未得到广泛应用。

图7 FPGA在计算全息3D显示中的应用Fig.7 Application of FPGA in computer-generated holographic 3D display

3.5 深度学习法

近几年，得益于GPU 计算能力的提高，深度学习法被应用于人工智能的各个领域［24］，计算全息技术也与深度学习法产生了紧密结合［25］。基于在计算全息实验中产生的大量数据，深度学习法利用成熟的深度学习框架，建立3D 物体的全息图与3D 物体间的损失函数关系，完成对神经网络的训练。当神经网络被训练完成后，可以快速生成满足需求的全息图，从而解决全息显示质量与计算时间的权衡问题，为计算全息图的快速生成提供了新的思路。日本大阪大学的研究人员提出了一种相对简单的深度神经网络训练数据生成策略，使用卷积残差神经网络生成3D 物体的全息图［26］，单帧全息图的计算时间仅需26 ms。韩国首尔大学的研究人员基于由随机点产生的训练数据集，提出了一种用于生成多深度全息图的深度神经网络［27］，当物体层数为5层时，多深度全息图的计算时间为234 ms。上海大学的研究人员利用多深度平面的角谱算法来训练卷积神经网络，实现了多层3D 物体的纯相位全息图的快速生成［28］。日本千叶大学的研究人员提出了将低采样全息图转换为全采样全息图的卷积神经网络，以补偿因采样不足引起的误差，同时加快了计算速度［29］。清华大学的研究人员以U-Net结构作为编码器生成全息图，在150 ms内完成了单帧分辨率为3940×2160 的全息图计算［30］，如图8（a）所示。麻省理工学院的研究人员提出了一种用复杂数据集训练深度神经网络的CNN 框架［31］，解决了传统计算全息中的遮挡问题，实验结果如图8（b）所示，为实时的全息3D显示提供了解决思路。

图8 深度学习在计算全息3D显示中的应用Fig.8 Application of the deep learning in computer-generated holographic 3D display

如今，理想的全息3D 显示对计算速度和重建质量都提出了很高要求，如何保证全息图在快速生成的同时也能有较好的重建质量是未来全息3D 显示技术研究的重点内容，深度学习法也将与计算全息技术结合得愈发紧密。

4 结论

本文对计算全息图的快速生成方法与优缺点进行了分类概述。在点元法中，LUT法和WRP法在加快点元法计算速度的同时节省了存储空间；解析面元法利用仿射变换减少了傅里叶变换次数，从而提高了传统面元法的计算速度；不断改进的分层法在解决遮挡问题的同时也加快了全息图的生成速度；硬件加速技术可以使计算速度得到大幅提升，而深度学习方法在保证质量的同时，也为全息图的快速计算提供了新的思路。目前，虽然国内外的研究人员提出了诸多提高全息图生成速度的方法，然而全息图的计算速度尚难以满足3D 物体实时计算的需求。未来，全息图的速度提升不仅需要高效率的计算方法，更需要高性能的硬件设备的开发。随着光电技术的发展，相信在不久的将来，3D 物体全息图的实时计算会得以实现。