采用转子开槽的内置永磁电机噪声抑制
2022-10-11陈明轩尹红彬高永超刘从臻
陈明轩,尹红彬,高永超,石 翔,刘从臻
(1.山东理工大学交通与车辆工程学院, 山东 淄博 255000;2.国网山东省电力公司烟台市牟平区供电公司, 山东 烟台 264100)
0 引言
随着电工技术、机械行业的迅猛发展,电机在各领域内被广泛使用。而永磁同步电机最受重视[1],其中,内置式V型永磁同步电机因其运行效率高、过载能力强、弱磁扩散能力强,而广泛地应用于电动汽车驱动领域。同时因其结构复杂、电磁振动噪声较大而存在诸多问题。因此,有必要对永磁电机的振动和噪声问题开展深入研究。
永磁同步电机的结构复杂、工作点不易确定,使用解析法工作量繁重,所以对其分析通常采用有限元法,国内外学者也在此方面做了不少的研究。文献[2-3]利用有限元软件分析了多种槽极数配合类型对电机的电磁振动和噪声的影响。文献[4]提出在定子齿内表面开设辅助槽来抑制振动,并通过仿真对比分析了辅助槽槽数、槽的深度、槽的形状、槽口宽、槽间间距等因素与齿槽转矩的关系。文献[5]通过把空间与时间分离,分别计算了定子的振动加速度,并与传统方法的结果进行了比较。文献[6]针对一台12极36槽内置式电机进行分析,结果表明零阶36倍频的径向电磁力波分量对电机的振动影响较大。文献[7]使用有限元软件精确计算多物理场中的噪声,其中包括切向力和阻尼比对噪声计算的影响。文献[8]提出了一种电机转子轴振动噪声模型的计算流程,同时也研究了许多关于变速永磁同步电机振动噪声的问题。文献[9]描述了8极48槽PMSM径向力波、噪声来源,并解释了电机噪声受单壳体刚度、前后端盖的影响。文献[10-13]利用有限元软件仿真对电机进行模态分析,分析计算各部件的固有频率,并通过实验验证了有限元的准确性。文献[14]分析了永磁同步电动机的模态,通过改变定子内表面偏移距离来探讨气隙内径向磁密的不均匀性,并总结出振动减小的方法。文献[15]提出通过开槽可以间接改变分数槽永磁电机的极槽数配合,以达到削弱激振力波的目的,并采用机械阻抗法对比开槽前后的噪声声功率级频率。
目前,已有永磁同步电机振动与噪声方面研究多数是从定子分析并展开,对转子的研究较少。本文以内置式V型永磁同步电机为研究对象,建立其二维有限元模型,提出一种转子表面开弧形槽的结构来减小转矩波动和电磁力,减少谐波次数,以达到抑制振动和噪声的目的。
1 电机基本参数及模型
针对内置式V型永磁同步电机开展分析研究。表1列出了电机参数,依据其建立有限元模型,如图1所示。

表1 电机参数

图1 原型电机有限元模型示意图
2 电磁激振力
定子上存在电磁力是引发电磁噪声的主要来源。根据麦克斯韦张量(Maxwell Tensor)法,定子内表面上的径向力密度为

(1)
式中:pr为电磁力密度,N·m-2,μ0为真空磁导率,其值为4π×10-7H·m-1,Bt为气隙磁密的切向分量,Br为径向分量。Br远大于Bt,计算电机时一般忽略切向分量[16]。
Br=Fr·Λ
(2)
Bt=Ft·Λ
(3)
(4)
式中:Fr为气隙磁动势,Ft为电枢磁动势,Λ为等效气隙磁密导,Λ0为其恒定幅值,Λn为n次谐波幅值,Q为槽数,θ为电角度。
Fr=∑F1cos(pθ-ωt)
(5)
(6)
式中:F1、F2分别为气隙、电枢的磁动势幅值,t为时间,φ为初始相位角,正负号则是磁场旋转的方向。
将式(1)—(6)联立可以得到定、转子谐波次数,其气隙定子和转子产生的谐波为[11]
u=2k1±1k1=0,1,2,…
(7)
v=2mk2-1k2=1,2,3,…
(8)
式中:v、u为定、转谐波次数,m为相数。
定、转子谐波产生的电磁力波阶数和相应的频率为
r=(v±u)p
(9)
fr=(1±u)f
(10)
力波幅值和力波阶数直接影响振动与噪声,力波阶数越低,振动和噪声越明显。反之,亦然。
根据以上公式,计算得出8极48槽电机可能存在的各阶次电磁力波,如表2所示。
对电磁力波进行解析推导可以得出存在不同阶次的电磁力波,但是不能精确得到其幅值大小。使用有限元软件对气隙磁场进行计算,并对结果进行FFT变换可以得出较为精确的各阶次幅值[17]。

表2 径向电磁力波阶数及频率倍数
3 模态分析
永磁同步电机因其较高的转矩密度和功率密度,运行时对其结构会有影响,所以准确的结构模态仿真预测对研究振动噪声具有重要意义。实际上,因为定子槽的存在导致定子结构复杂,而且槽满率对弹性模量等材料的参数也产生不可忽视的影响,这使得划分的网格质量较差,需要对结构进行必要的简化。本文将绕组等效为与实际体积相同的空心圆柱体;绕组密度依据绕组中线圈、软磁材料和气隙长度的比值等效,不计螺纹等细小结构。图2为三维壳体和定子的结构模型,表2是各部分材料参数。

图2 壳体和定子结构模型示意图
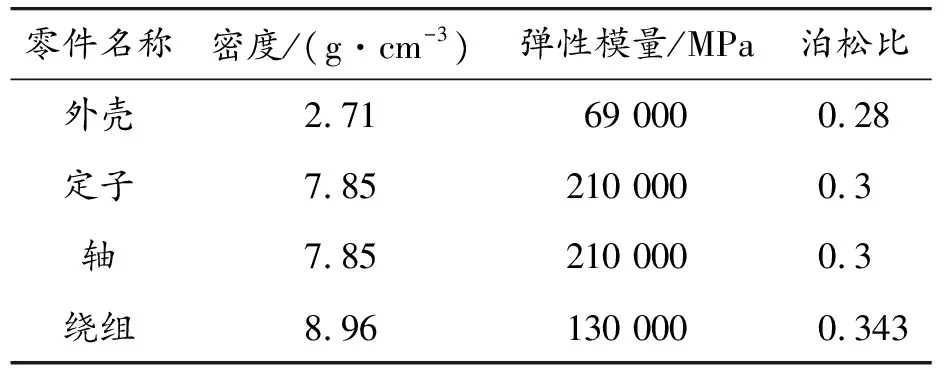
零件名称密度/(g·cm-3)弹性模量/MPa泊松比外壳2.7169 0000.28定子7.85210 0000.3轴7.85210 0000.3绕组8.96 130 0000.343
为了提高电机各个部件网格的细分程度,采用分层法,不同部件使用的不同的划分标准生成高质量网格并建立简化模型,图3为仿真计算所得电机结构模态结果。

图3 电机结构模态示意图
其中,变形量与力波次数的四次方成反比,因此高阶电磁力波不易引起振动,所以低阶力波模态是研究的重点。
图3中,2阶固有频率是2 270.60 Hz,3阶固有频率是5 188.99 Hz。电机正常工作时应避免力波频率与模态频率接近,否则会出现共振的情况。
4 槽尺寸与位置选择
为了降低电机的振动与噪声,本文提出转子表面开槽的优化方案,以圆形转子为优化对象,在其表面开槽,定义辅助槽为弧形槽,其三维优化模型如图4所示。

图4 二维优化模型示意图
转子表面开槽的大小和位置会改变电机气隙磁密不饱和区域的位置,影响气隙磁密分布,从而影响振动与噪声,所以准确设计弧形槽的尺寸和位置显得尤为重要[18]。以弧形槽为例,采用控制变量法保持弧形槽深0.4 mm,以每一磁极d轴(直轴)为开槽中心线起点,偏移d轴角度(α=0°~17°),向两边偏移,选择步长为1°进行参数化扫描,选择出最佳的角度匹配,经有限元分析得到齿槽转矩峰值及径向电磁力峰值随偏移角度的变化,如图5所示。
根据图5齿槽转矩峰值和径向电磁力峰值随角度的变化以及优化前的齿槽转矩的变化,齿槽转矩随角度变化不定,径向电磁力整体趋势是先增大后减小,与图5(b)优化前的齿槽转矩峰值相比在1°、8°、15°处开槽时明显降低,而径向电磁力在15°时要小于大部分角度的电磁力,本文选择15°偏移角度进行研究。
保持弧形槽偏移角为15°不变,将弧形槽深设置为变量,其取值定为0.1~0.6 mm,步长设置为0.1 mm,研究其对齿槽转矩和径向电磁力的影响规律,仿真得到的结果如图6所示。

图5 齿槽转矩、径向电磁力随偏移角度的变化

图6 齿槽转矩、径向电磁力随槽深的变化
由图6可知,在槽深的变化范围内,齿槽转矩峰值随弧形槽深度加深先减小后增大,而径向电磁力峰值随槽深加深呈一直减小的趋势,齿槽转矩峰值在槽深为0.5 mm时最低,而径向电磁力峰值在槽深为0.6 mm时最低。从图7中可看出,随着槽深的不断增大,径向磁密傅里叶变换后的基波也不断减少,考虑到可能会使性能下降,选择槽深为0.3 mm。
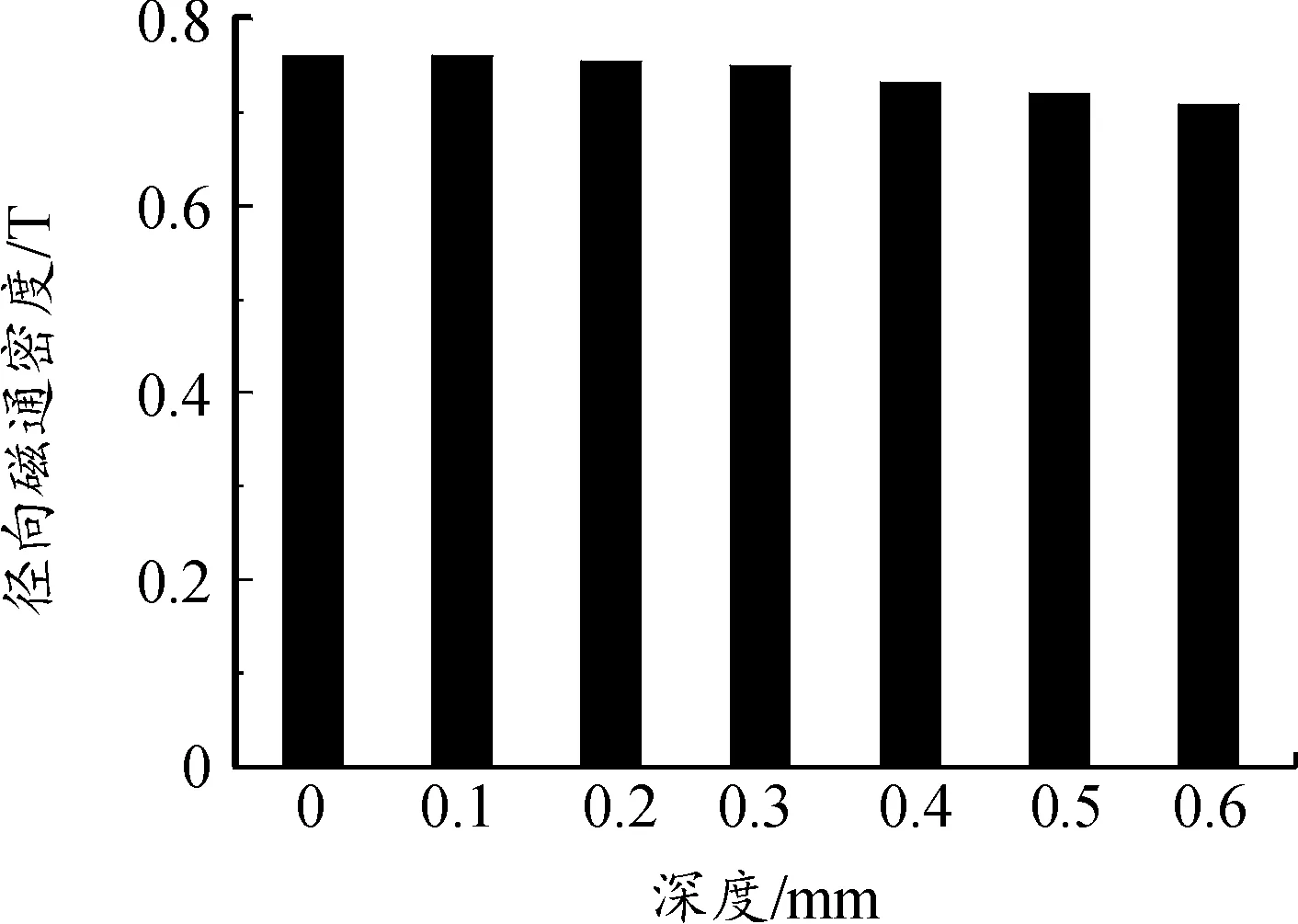
图7 基波径向磁通密度与槽深的关系
5 电机机械强度校核
转子在高速旋转时,其结构承受很大的离心应力,应力大的部位可能会发生局部形变。为保证优化后电机的可靠性和安全性,有必要对转子结构承受的离心应力及其结构形变量进行有限元仿真。当电机高速运行时,分析模型中承受最大应力的大小和位置,校对模型结构的机械可靠性。转子的材料特性参数如表3所示。转子结构3D有限元离心力仿真模型在高速空载下获得的应力云图和结构形变云图如图8所示。

表3 转子材料特性参数

图8 高速空载下转子应力云图与结构形变云图
图8(a)是在空载最高转速10 000 r/min下转子结构所受离心力的应力仿真云图。可见,最大离心应力分布在转子隔磁桥内,应力最大值为151.7 MPa,而硅钢片的屈服极限是410 MPa,旋转过程中是不会产生塑性变形。
离心应力导致的转子结构形变云图如图8(b)。转子结构最大形变为0.007 mm,而电机气隙是0.75 mm,其形变量远小于气隙长度,从运行可行性来看,旋转过程中定、转子不会碰撞,相对较安全。优化后转子结构的机械强度可行。
6 噪声与振动响应
转子表面开槽后其气隙长度被改变,气隙磁密分布也发生变化。转子表面开弧形槽前后的气隙磁密分布曲线与气隙磁密傅里叶分解谐波分别如图9所示。
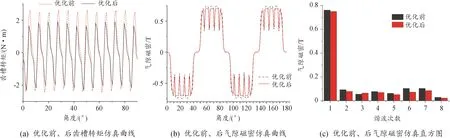
图9 优化前、后齿槽转矩和气隙磁密等仿真结果
图9(a)为开设辅助槽前后的齿槽转矩仿真结果。由图可见,在0°~90°的范围内齿槽转矩呈周期分布,优化后转矩最大值为1.901 N·m,较优化前最大值2.664 N·m下降约28%。
图9(b)为气隙磁密优化前后的仿真结果。由图可见,优化后的气隙磁密幅值略有下降,优化后的气隙磁密波形更趋向于正弦,改善了气隙磁密的波形。从图9(c)可以看出,气隙磁密基波基本不变,对电机性能不会有太大的影响,气隙磁密2、4、5、6、7、8次谐波各有不同程度的减小。
根据上述模型对电机进行振动响应分析。转速为3 000 r/min时,电机壳体的振动加速度云图如图10。

图10 壳体外表面加速度云图
由图10可以看出,优化后电机的整体加速度峰值有所下降。提取壳体外表面加速度响应,图10(a)、(b)中,当模型处于800~1 260 Hz范围内,在960 Hz对应点处出现振动加速度最大值,优化后振动加速度峰值下降了0.288 6 m/s2,同时壳体整体上也有下降的趋势;图10(c),(d)中,当模型处于1 440~2 700 Hz范围内,在1 560 Hz对应点处出现振动加速度最大值,优化后振动加速度峰值下降0.290 5 m/s2;图10(e),(f)中,在3 000~3 960 Hz范围内,3 120 Hz处出现振动加速度最大值,优化后振动加速度峰值下降0.113 5 m/s2。
对模型进一步分析可得声压分布,这里采用球面辐射进行仿真,建立直径位600 mm的球状辐射模型,仿真分析得出球体表面的声压级[19]。从图11声压级仿真结果云图可以看出,噪声在不同频率范围内均有所降低。
图11(a)、(b)显示,在径向电磁力的激励下,当模型处于2 400~3 000 Hz频率范围内,2 520 Hz处出现电磁噪声峰值,优化后峰值降低1.797 8 dB,且整体看来噪声也有所下降;图11(c)、(d)显示,当模型处于3 320~3 800 Hz频率的声压级响应中,3 480 Hz处出现了阶段性的噪声峰值,优化后峰值降低6.276 2 dB。

图11 声压级仿真结果云图
转子表面开槽增长了气隙有效长度,使得磁阻增大,穿过辅助槽的磁力线将减少,也就使得辅助槽底部与永磁体之间的磁力线增多,导致磁力线走向和磁通密度也与之前不同,影响了径向气隙磁密分布,从而影响到电磁力和噪声。
由以上的分析结果可知,转子结构的优化有利于降低电机的振动与噪声,故此优化方案可行。
7 结论
以一台8极48槽内置式永磁同步电动机为研究对象,提出了通过电机转子表面开槽降低电机振动和噪声的方案,并仿真分析了电机的模态、电机加速度响应和声压级。
1) 对转子表面开弧形槽简单可行,不仅降低了径向电磁力、齿槽转矩,而且减小了振动加速度和噪声。
2) 永磁同步电机结构复杂,对电机噪声与振动准确预测,对节约电机研发成本、缩短研发周期具有重要意义。
