螺旋面工件各离散点处一阶导数的计算方法研究

2022-10-11丁康康方素平周丽华

合肥工业大学学报（自然科学版） 2022年9期

丁康康, 方素平, 周丽华

(合肥工业大学机械工程学院,安徽合肥 230009)

0 引言

设计、计算、加工离散点截形螺旋面工件成形刀具是一项非常复杂的工程。根据已知条件的不同,具体需要经过各离散点处一阶导数的计算、接触条件方程式的求解、工件端面廓形坐标系的转换、刀具截形参数的求取等步骤。其中,求取各离散点处的一阶导数作为整个计算过程的基础步骤,其计算精度的高低将直接影响后续步骤的计算精度。文献[1-3]研究了利用三次样条函数法以及三次参数样条函数法的计算方法。三次样条函数能够保证各型值点处有连续的一阶导数及二阶导数,使得在不用对离散点进行拟合的情况下便可以完成一阶导数的计算,简化了计算步骤,提高了计算效率;但必须满足“小挠度”要求,否则求出的一阶导数值误差较大。而利用累加弦长的参数样条法,即在构造普通三次样条函数的基础上,分别计算相邻2个型值点连线的长度,将普通三次样条函数转化为各型值点横、纵坐标关于累加弦长的三次样条函数;但因未考虑数据点相邻弦线的折拐情况,导致在截形曲率变化较大处计算误差较大。文献[4]研究了基于标架与直角坐标系相结合的方法来确定螺旋面方程,进而求其一阶导数，利用标架确定螺旋面方程,再将其转化成直角坐标方程;但该方法计算过程复杂,并且通用性不高,需先确定螺旋面方程。

针对上述所提出的计算方法均未解决离散点截形“大挠度”条件[5]下求其一阶导数时计算精度不高的问题，本文提出一种新的计算方法,在构造三次样条函数的基础上,以累加弧长为参变数,利用累加弧长的参数样条法来计算各离散点处的一阶导数,以达到更高的设计精度。

1 累加弧长的参数样条法

1.1 累加弧长的定义

图1 工件端面截形

(1)

1.2 各分段圆弧弧长的求取方法

要想求得各分段圆弧的长度,需先确定各分段圆弧所在圆的圆心位置[6]。由圆的方程(x-x0)2+(y-y0)2=R2可知,要确定一个圆必须有3个独立的条件。例如，过不在同一直线上的3个点可以作1个圆，已知2个点和其中1个点的切线斜率也可以确定1个圆等。因此可对上述问题做如下考虑。

(1) 已知圆上两点A0(a0,b0)、A1(a1,b1)及其中一点处的斜率,求圆P0。

(2) 已知圆P0和圆外一点A2(a2,b2),求圆P1,使它通过定点A2,并且与圆P0相切于定点A1。

(3) 已知圆Pn-1和圆Pn-3,求圆Pn-2,使它和圆Pn-1相切于点An-1,并且与圆Pn-3相切于点An-2。

(1) 对第一类问题的求解分析如图2a所示。由点A1(a1,b1)、点A0(a0,b0)及其斜率k0所确定的圆,其圆心P0一定既在直线P0A0上,又在直线A0A1的垂直平分线上。令A0A1的中点为B(u,v),则只需求直线P0A0与直线P0B的交点即可确定点P0(xP0,yP0)。

由点A0处的斜率为k0可得直线P0A0的斜率为-1/k0,则直线P0A0可表示为:

y=b0-(x-a0)/k0

(2)

直线P0B的函数表达式为:

y=v-(x-u)/k1

(3)

其中,k1=(b1-b0)/(a1-a0)。

联立(2)式和(3)式便可求得圆心P0的坐标为:

圆心坐标一旦求出,则由其所确定的圆的半径为:

再根据ΔA0P0B的三角函数关系,可求得:

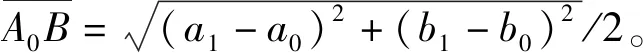
l1=2R0α0，

ln=2Rn-1αn-1。

(2) 第二类问题的求解分析如图2b所示。设圆P0的圆心坐标为(xP0,yP0),半径为R0;设所求圆P1的圆心坐标为(xP1,yP1),半径为R1。P1既要在A1A2的垂直平分线上,又要在A1P0的连线上,因此只要求出这2条直线的交点,便可确定其圆心位置。

直线A1P0的方程为：

y=b1+k0(x-a1)

(4)

其中,k0=(b1-yP0)/(a1-xP0)。

A1A2垂直平分线的方程为：

y=v+k1(x-u)

(5)

其中,k1=(a2-b1)/(b1-b2)。

联立(4)式和(5)式可以解得：

l2=2R1α1。

图2 各分段圆弧弧长求解示意图

直线Pn-2An-2的方程为：

y-bn-2=kn-2(x-an-2)

(6)

其中，kn-2=(bn-2-yPn-3)/(an-2-xPn-3)。

直线Pn-2An-1的方程为：

y-bn-1=kn-1(x-an-1)

(7)

其中，kn-1=(bn-1-yPn-1)/(an-1-xPn-1)。

联立(6)式和(7)式可得：

ln-2=2Rn-2αn-2，

至此,上述求各分段圆弧弧长的问题得到解决，可以根据不同约束条件选取不同的计算方法。各分段圆弧弧长求出以后,便可根据(1)式计算累加弧长。

1.3 各离散点处一阶导数的求取

在已知工件轮廓首尾端点处一阶导数的条件下:设首端点处一阶导数为k0。尾端点处一阶导数为kn。在相应的累加弧长求出以后,可以分别构造横坐标x关于参变数s的三次样条函数x(si)以及纵坐标y关于参变数s的三次样条函数y(si)(具体构造方法文献[7]中已详细介绍,限于篇幅,这里不再赘述)。对所构造的三次样条函数分别求其各点处的一阶导数(dx/ds)i和(dy/ds)i,并为其添加边界条件，即

最后将得到的2个三次样条函数合并得到累加弧长的参数样条曲线P(si)=(x(si),y(si))(i=0,1,2,…,n),其上各节点(xi,yi)处的一阶导数为:

2 计算软件设计

求取各离散点处的一阶导数,计算过程复杂。根据不同工件计算精度的要求,其端面廓形可能会有上百个坐标点组成,这是一项手工无法完成的任务。为此,有必要根据求解原理,编写相应的计算软件,以达到快速、精确计算各离散点一阶导数的目的。根据软件的功能要求,计算软件应能完成数据文件类型的选择、截形参数的读取、各分段圆弧弧长的计算、三次样条函数的构造、离散点一阶导数的求取等。

设计计算软件的实现界面如图3所示。

软件系统的功能模块主要包括人机交互界面、数据文件类型的选择模块、加工参数输入模块、离散数据处理模块、端面廓形方程处理模块和各型值点一阶导数计算模块。程序以人机交互界面为主框架,集成其他功能模块的触发命令。其他模块以人机交互界面为基础,通过数据接口与其进行数据交换。与此同时,设置数据保存按钮,以便及时保存计算所得数据结果。设置列表视图控件作为主显示界面,以实现数据计算结果的实时显示。

程序的计算流程如图4所示。

图4 程序计算流程

在求得各型值点一阶导数以后,通过求解接触条件式[8],解出各型值点成为刀具回转面与工件螺旋面的接触点时所旋转的角度,进而求解刀具截形参数。将所得刀具截形数据文件导入CAD系统,模拟形成刀具廓型线,然后利用CAD系统的三维建模功能,即可创建刀具的三维实体模型。

3 计算实例

3.1 工件端面截形计算参数

已知螺旋面工件的端面截形如图5所示。

图5 工件端面截形

其中:r1=15 mm;r2=30 mm;外圆螺旋角β=30°;旋向为右旋。对于轴对称的工件截形,为使刀具廓形对称,减少计算的工作量,一般选x轴为工件截形的对称轴。为便于比较不同计算方法的计算精度,本文选取端面截形方程已知的截形曲线。由图5可得工件的端面截形方程为:

其中，u为参变数,考虑对称性,故只需计算螺旋面工件的半边截形尺寸,因此有最大角度参变数umax=cos-1[r1/(2r2)]=75.525°,最小角度参变数umin=0°。

3.2 各离散点一阶导数的计算

根据工件的截形尺寸范围,先选定一系列u值,u值范围应考虑使计算范围比齿面的有效部分稍大[9],u值的间隔大小(即计算点的多少)视计算精度要求而定。将选定的u值代入端面截形曲线方程,得到一系列离散点坐标。分别利用文献[8]和文献[10]中的三次样条法、累加弦长的参数样条法以及本文提出的累加弧长的参数样条法计算各离散点处的一阶导数,并将其与理论值作比较,分析计算误差。所选定的参变数u以及对应离散点坐标见表1所列,所得计算结果见表2所列。其中:k0表示理论值;k1表示由三次样条法计算所得值;k2表示由累加弦长计算所得值;k3表示由累加弧长计算所得值。

表1 各离散点坐标及对应的参变数

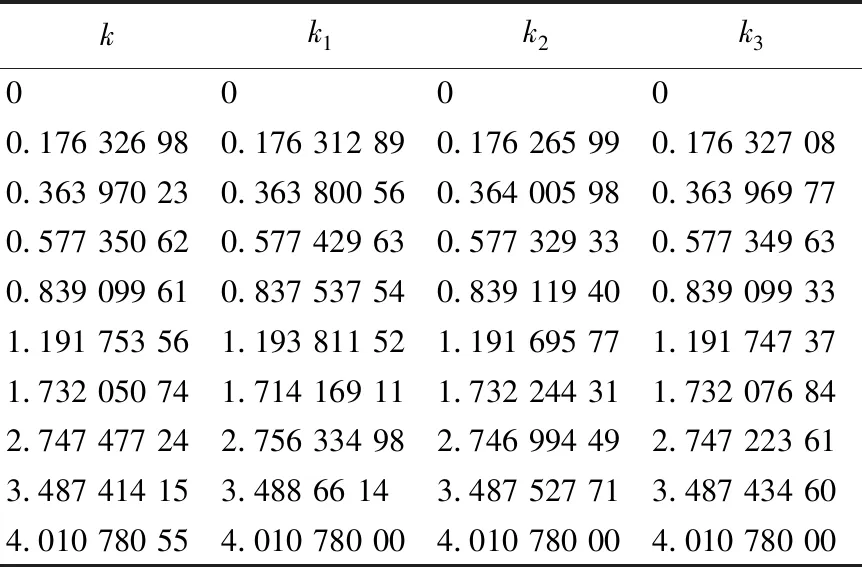
表2 计算结果

由表2可知,以参数方程经求导运算所得结果作为标准值,在选取同样离散点坐标及截形角度参变数的情况下,利用三次样条法计算所得最大相对误差为|k1-k0|/k0=10.324‰,利用累加弦长的参数样条法计算所得最大相对误差为0.176‰,利用累加弧长的参数样条法计算所得最大相对误差仅为0.092‰,计算精度达到0.1 μm。