分段杆弹的梯度化设计
2022-10-11喻争王舒董方栋郑志军崔世堂张永亮
喻争, 王舒, 董方栋, 郑志军, 崔世堂, 张永亮,
(1.中国科学技术大学 近代力学系 中国科学院材料力学行为和设计重点实验室, 安徽 合肥 230026;2.中国兵器工业第208研究所 瞬态冲击技术重点实验室, 北京 102202)
0 引言
随着装甲的不断升级,普通穿甲弹对装甲的侵彻破坏能力日渐式微。动能武器,尤其是长杆弹逐渐成为了近年来兵器领域研究的热点。但由于发射条件的限制,不断提高长径比以增加长杆弹侵彻深度的方式逐渐失效。20世纪80年代,有学者提出了分段杆弹的概念。分段杆弹是指将长杆弹弹体人为分为长径比较小的独立弹体的一种新型弹药形式。文献[1-3]研究结果表明,在相同的质量下,分段杆弹侵彻效率高于长杆弹。如何发挥出分段杆弹最大的侵彻效能成为研究的热点问题。
实验方面,Cuadros对带铝套筒的钨合金分段杆侵彻装甲钢进行了速度2~4 km/s的弹道实验,结果表明在1~3倍弹径范围内增大各段之间的间隔可增大分段杆侵彻深度。Sorensen等的实验结果证明,在分段杆弹各段之间填充玻璃纤维会降低侵彻效率。Franzen实验证明在相同质量、直径、速度和总长度条件下不断减小各段长径比并不能无限提高侵彻深度。Wang等实验研究了铝套筒对分段杆弹侵彻的影响,发现套筒对侵彻深度有一定贡献。随着数值模拟技术的发展,对分段杆弹的研究逐渐深入。Normandia等利用轴对称模型计算了速度2.6 km/s下长径比小于1的分段杆弹对半无限钢靶的侵彻过程,表明前段残留物会减小后段侵彻效率,通过技术手段去除残留物可以进一步提高分段杆弹侵彻深度。Tate提出了简化模型以评估前段残留物对后段弹体侵彻的影响,并据此优化了分段杆各段之间间隔从而提高分段杆侵彻能力。Littlefield和Lee研究了斜置分段杆弹对斜置分层靶板的侵彻,发现合理斜置分段杆可以提高侵彻深度。Jo等研究了相同的问题,发现增加分段之间间隔和各段长度可以提高分段杆对分层靶板的侵彻深度。朗林等、胡静等、邓云飞等、Cao等用光滑粒子算法研究了不同连接形式对分段杆侵彻深度的贡献。蒋建伟等研究了分段数目、间隔等对侵彻深度的影响,特别研究了不同形状头部对侵彻的影响,发现尖锥形、球形和截锥形头部均优于圆柱形头部。陈建良等研究了钨纤维对分段杆侵彻性能的增强效应。由此可见对分段杆弹的研究集中在最优长径比、最优分段间隔、弹体形状、材料等方面,但在实际应用中,分段杆弹之间的间隔会造成弹体过长,造成分段杆弹的发射困难以及侵彻过程中的不同轴。因此在保证侵彻深度的前提下尽可能减小长度是分段杆弹研究设计的重要目标之一。梯度化是对弹体结构优化设计的可行手段。但目前关于分段杆弹的梯度化设计研究较为匮乏。2019年,焦文俊等总结了分段杆弹侵彻的相关研究进展,建议继续对分段杆弹开展实验、模拟和理论研究,并提出要分析变密度(梯度变化或周期变化)杆等新弹体构型的侵彻性能。
本文分别构造了长度和直径梯度变化的分段杆弹,采用数值模拟方法对比研究了其侵彻效率,并对计算结果进行了理论分析。
1 侵彻过程数值模拟
1.1 参照实验
本文参照Charters等开展的实验进行数值模拟研究,对照其实验结果验证有限元模型的有效性。实验长杆弹结构如图1所示。

图1 长杆弹Fig.1 The long rod the segmented rod projectile
实验中的弹体为钨合金材料(钨镍铁合金),靶体为RHA(4340)钢。所述长杆弹弹体为均质圆柱形,直径为5.54 mm,长径比5;靶体尺寸为200 mm×200 mm。实验采用轻气炮发射,实验速度范围2.0~4.0 km/s。
1.2 有限元模型
对长杆弹、理想分段杆弹和靶板进行建模,考虑到研究对象具有对称性,采用1/4对称模型以缩短计算时间。长杆弹总尺寸5.54 mm×27.7 mm;考虑到求解规模,将靶板尺寸设置为70 mm×100 mm。经网格收敛性分析,模型求解结果随着网格变小收敛,考虑求解效率,确定网格大小为0.33 mm×0.33 mm。靶板靠近对称轴10 mm内单元尺寸为0.33 mm×0.33 mm,沿半径方向过渡。采用TrueGrid软件进行映射网格划分。弹、靶均采用3D solid164实体单元,总单元数245 840。弹、靶的对称界面采用对称约束,靶板下方界面采用全约束,外边界采用无反射边界以消除反射应力波的影响。弹、靶有限元模型如图2所示。
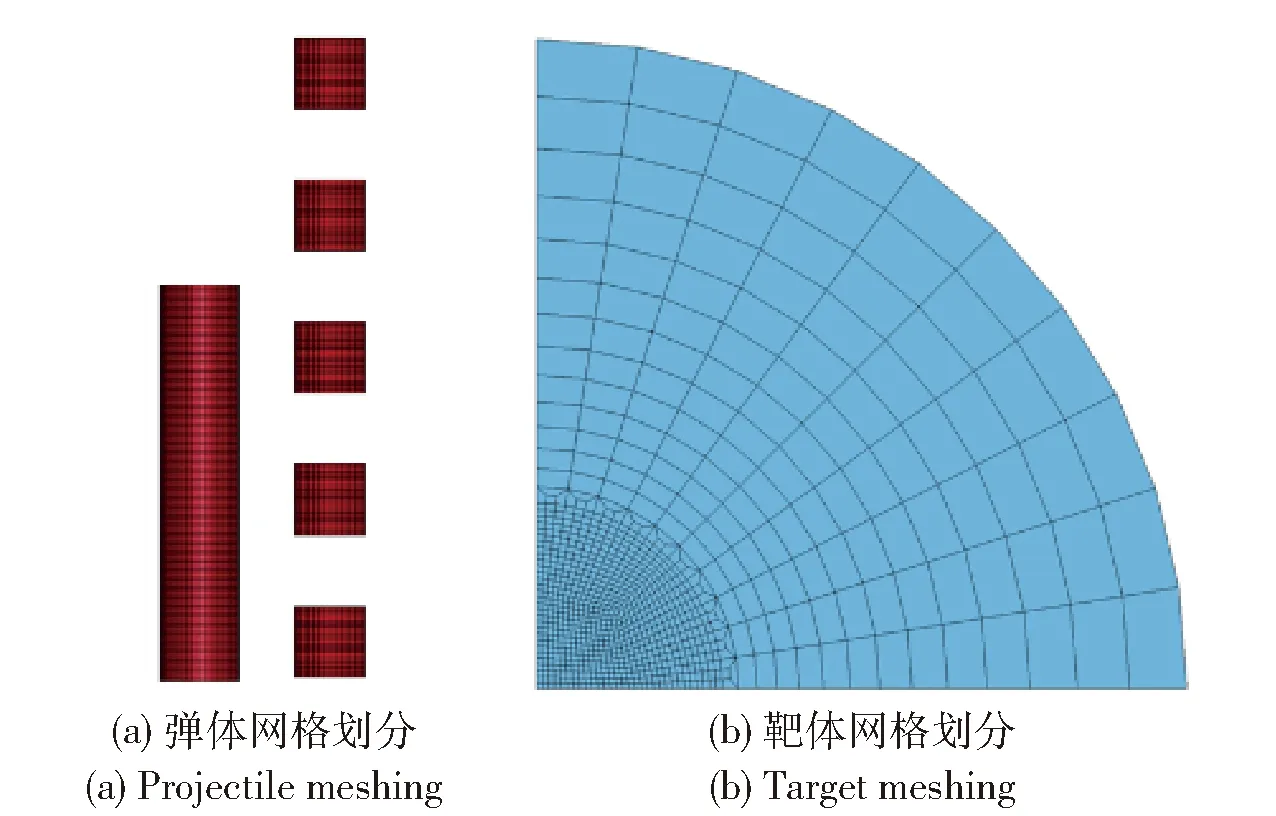
图2 有限元模型Fig.2 Finite element model of target and projectile
1.3 弹、靶材料本构模型及其参数
Johnson-Cook模型考虑了应变、温度和应变率对屈服应力的影响,是描述金属动态力学行为常用的本构模型,因此采用该模型描述弹体和靶体。模型数学表述为
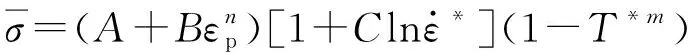
(1)
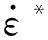
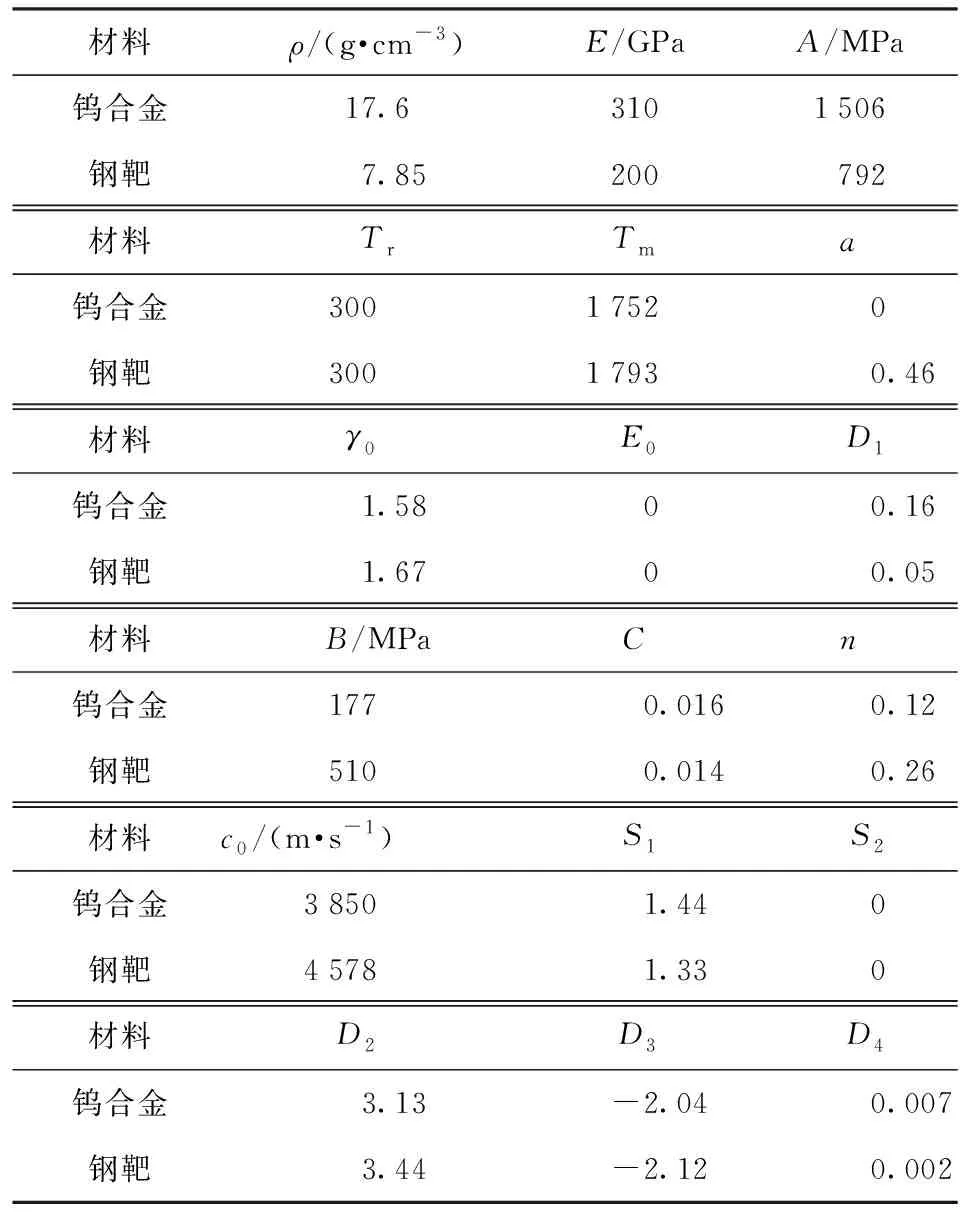
表1 弹、靶材料参数Table 1 Material parameters of target and projectile
1.4 单元删除和接触算法
采用Johnson-Cook材料损伤准则,即最大等效应变损伤准则。在计算时,材料超过弹性极限将产生塑性应变,当塑性应变积累到一定程度时材料损伤。数学表达式如下:
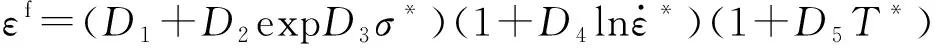
(2)
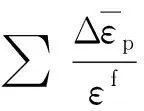
2 计算结果与实验对比
采用12节本构模型和参数对钨合金长杆弹侵彻钢靶的实验进行数值模拟。有限元计算所得侵彻深度与文献[18]实验结果的对比如图3所示。
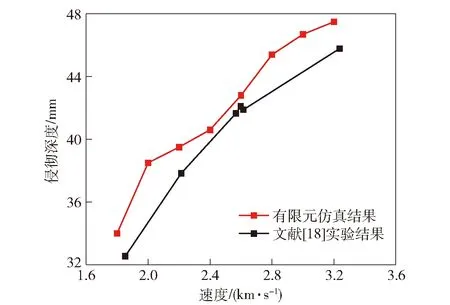
图3 侵彻深度有限元结果与实验结果对比Fig.3 Penetration depth FEM compared with EXP
由图3可见,随着速度的增大,实验与有限元计算所得侵彻深度呈相近的增大趋势。与计算值相比,长杆弹侵彻深度的实验值较小,这是因为长杆弹在实际侵彻过程中不是始终正侵彻,而是会与靶板呈一定角度。
图4给出了长杆弹侵彻过程中4个时刻的物理图像。由图4可见:=0 μs时刻,长杆弹以2 000 m/s的速度与靶板表面发生冲击,产生瞬时高压,靶板表面被击溃;=15 μs时刻,此时长杆弹速度几乎保持不变,进入准定常半流体侵彻阶段;=30 μs时刻,剩余弹体无量纲长度约为1,靶板进入后流动阶段。侵彻的最后阶段,剩余弹体动能殆尽,靶板回弹。
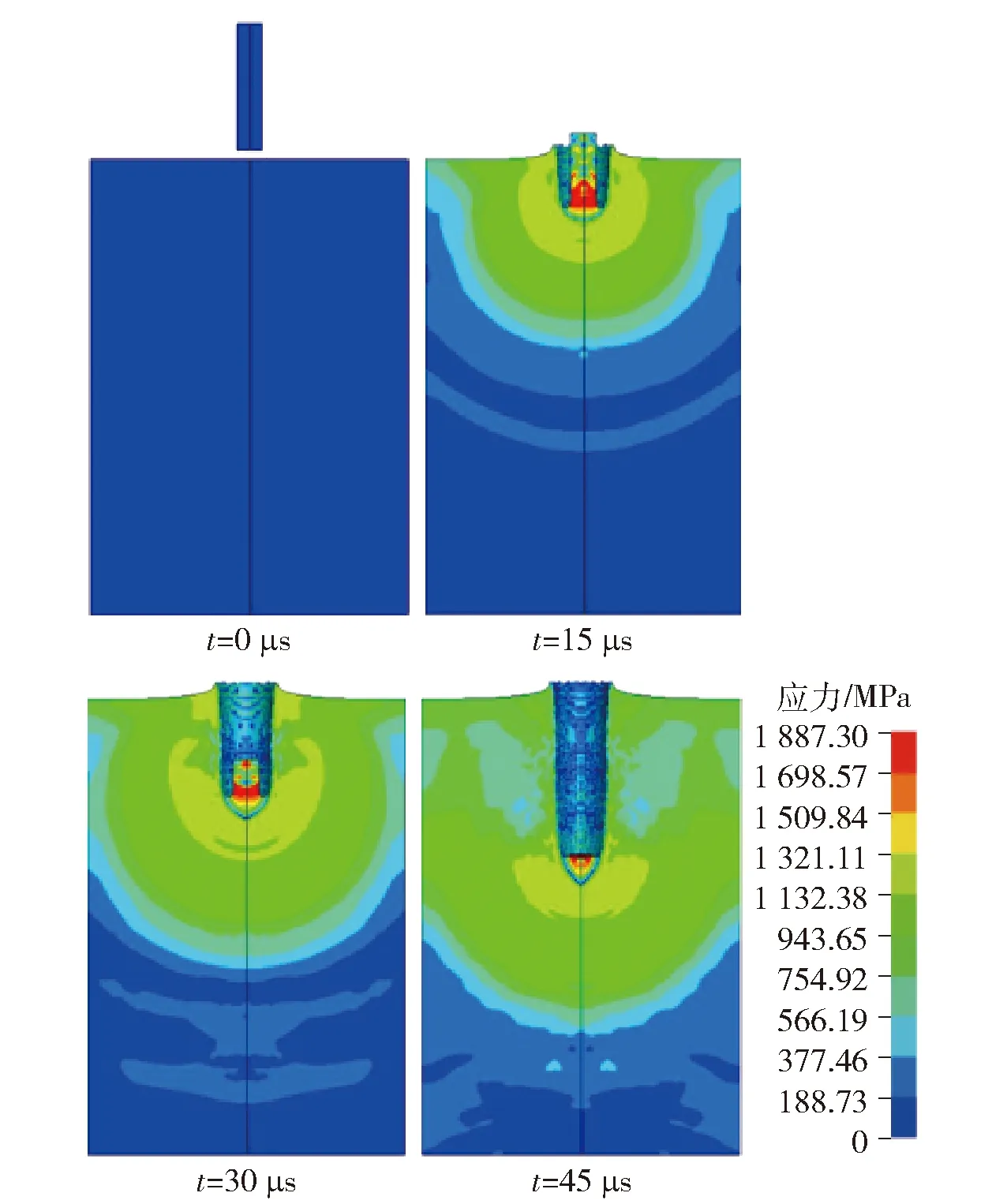
图4 长杆弹侵彻过程中弹体和钢靶的有效应力分布Fig.4 Effective stress distribution of projectile and target during penetration by long-rod projectile
长杆弹侵彻的4个阶段弹与靶板的接触力呈现出不同的特点。如图5所示,初始瞬态阶段(Ⅰ)出现压力陡峰,时间仅几个微秒;随后进入准定常侵彻阶段(Ⅱ),接触反力在某一恒值附近抖动,准定常阶段持续时间达25 μs左右,贡献了长杆弹绝大部分的侵彻深度;后流动阶段(Ⅲ)和靶板反弹阶段(Ⅳ)接触力逐渐下降,直至为0 kN。
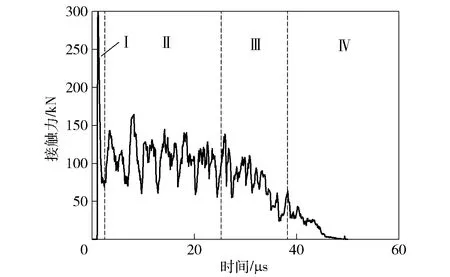
图5 弹- 靶界面接触力有限元仿真结果Fig.5 Projectile-target interface contact force FEM
图6为长杆弹侵彻半无限靶空腔形貌的数值模拟结果与实验对比情况,两者略有差异,但能够反映钨合金侵彻装甲钢的主要物理规律。总之,所构建的有限元模型及其采用的参数是可靠的,为分段杆弹的梯度化设计奠定了研究基础。
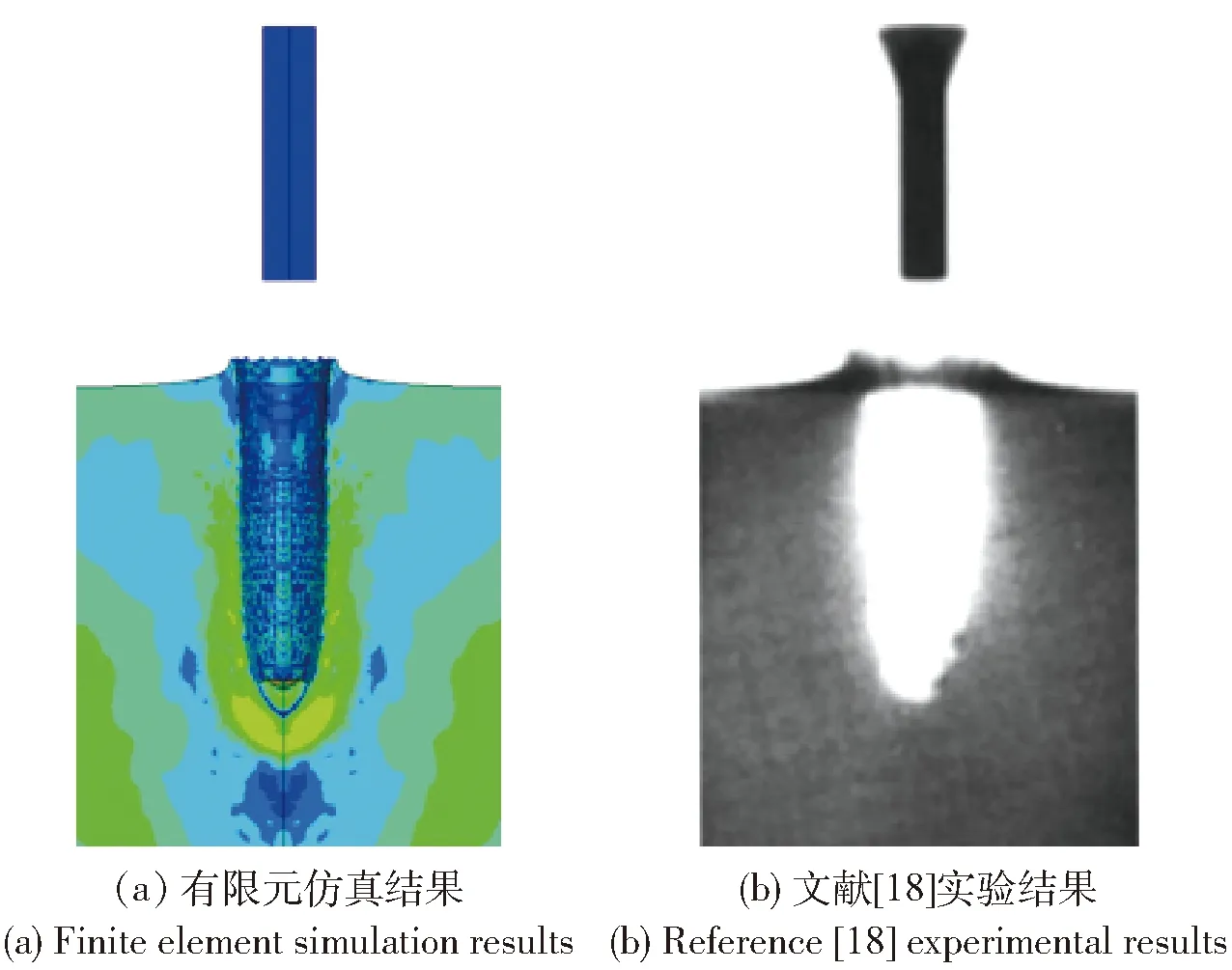
图6 长杆弹有限元仿真与实验[18]空腔形貌对比Fig.6 Cavity morphology of FEM versus EXP[18]
3 分段杆梯度配置侵彻效能对比
3.1 数值计算
本文构造了正梯度、负梯度和均匀分布的5种分段杆弹,如图7所示。所述的正梯度是指靶板法向方向上分段杆各段长度递增;负梯度是指法向方向上分段杆各段长度递减,均匀分布则是各段长度相等。梯度定义为前后两段杆的长度差。构造了梯度为0 mm的均匀分段杆、梯度为1 mm和2 mm正梯度以及梯度为-1 mm和-2 mm的负梯度共5种分段杆。段与段之间的间距取为前段杆的长度。
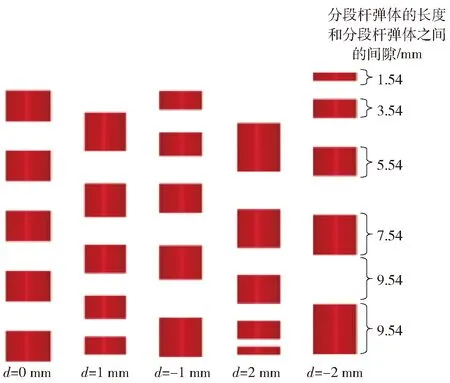
图7 梯度分段杆配置Fig.7 Gradient segmented rod configuration
=0 mm的均匀等长杆在速度=3 000 m/s的初速下侵彻靶板的等效应力云图如图8所示。由图8可见:=6 μs时,第1段杆与靶板发生冲击,应力波由接触面向靶板内部传播,靶板内部应力波阵面呈球形,在靶板界面处形成盆口;=10 μs时,第2段杆全部消蚀,第3段杆在前一段杆所形成的空腔基础上继续侵彻;=20 μs和=25 μs时,第3段杆和第4段杆继续侵彻;=30 μs时整个杆全部消蚀,侵彻深度达到最大,整个侵彻空腔呈糖葫芦串状。
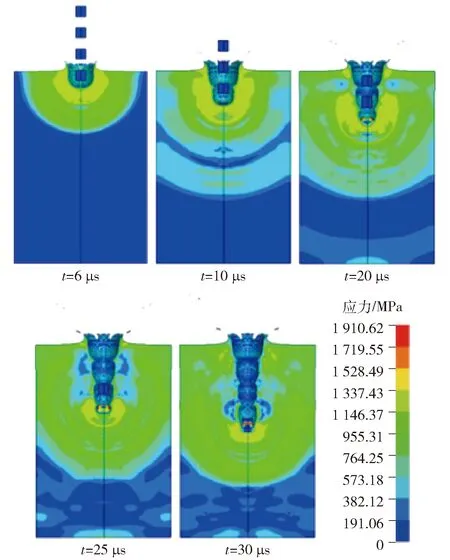
图8 等效应力云图Fig.8 von Mises stress contours
5种配置的分段杆在=3 000 m/s的初速下侵彻RHA半无限钢靶的最后侵彻深度如表2所示。由表2可见:均匀分布的分段杆侵彻深度为565 mm,整体侵彻效度113,表现最优。其余结果呈现侵彻深度以=0 mm为中心,逐步降低的趋势,且偏离值越大,侵彻深度降低得越多。

表2 梯度配置分段杆侵深Table 2 Penetration of segmented rod with different gradient configuration
分别取值为1 500 m/s、2 000 m/s和3 000 m/s的计算结果如图9所示,从中可见侵彻深度均表现出以=0 mm为中心、逐步降低的趋势,且偏离值越大,侵彻深度降低得越多。
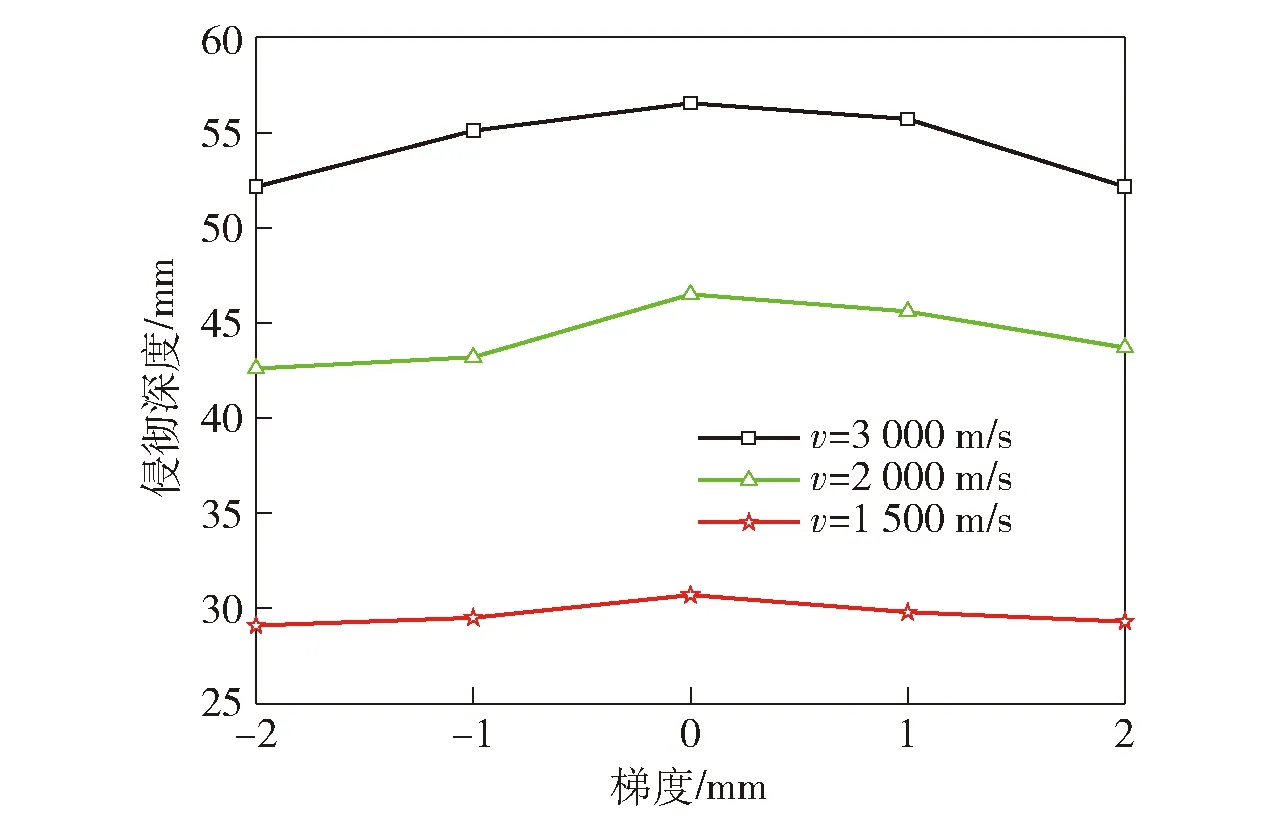
图9 不同速度下侵彻深度随等差值的变化曲线Fig.9 Variation curve of penetration depth with equidifference at different speeds
图10为等差配置的分段杆侵彻半无限靶后的截面。由图10可见:所有配置的分段杆整体截面形状都呈糖葫芦串状;各段所形成的空腔与长径比呈相关,即长径比越大,所形成的空腔越长;在弹- 靶界面处的空腔直径明显大于内部的空腔直径,且各配置分段杆的弹- 靶界面空腔直径近似相等,与长径比无关;靶板内部,各段空腔最大直径也近似相等,与所处位置和弹的长径比无关。

图10 等效塑性应变云图Fig.10 Effective plastic strain contours
3.2 理论分析
长杆弹侵彻的长径比效应是指随着长径比增加,消蚀单位长度杆所得到的侵彻深度减小。如图11所示,速度一定时,随着长径比的增大,无量纲侵彻深度呈现亚线性增加趋势。曲线斜率,即侵彻效率,随着长径比的增加逐渐减小。文献[21]系统描述了长径比效应。图11中,为侵彻深度,为长杆弹直径,为弹的长度。
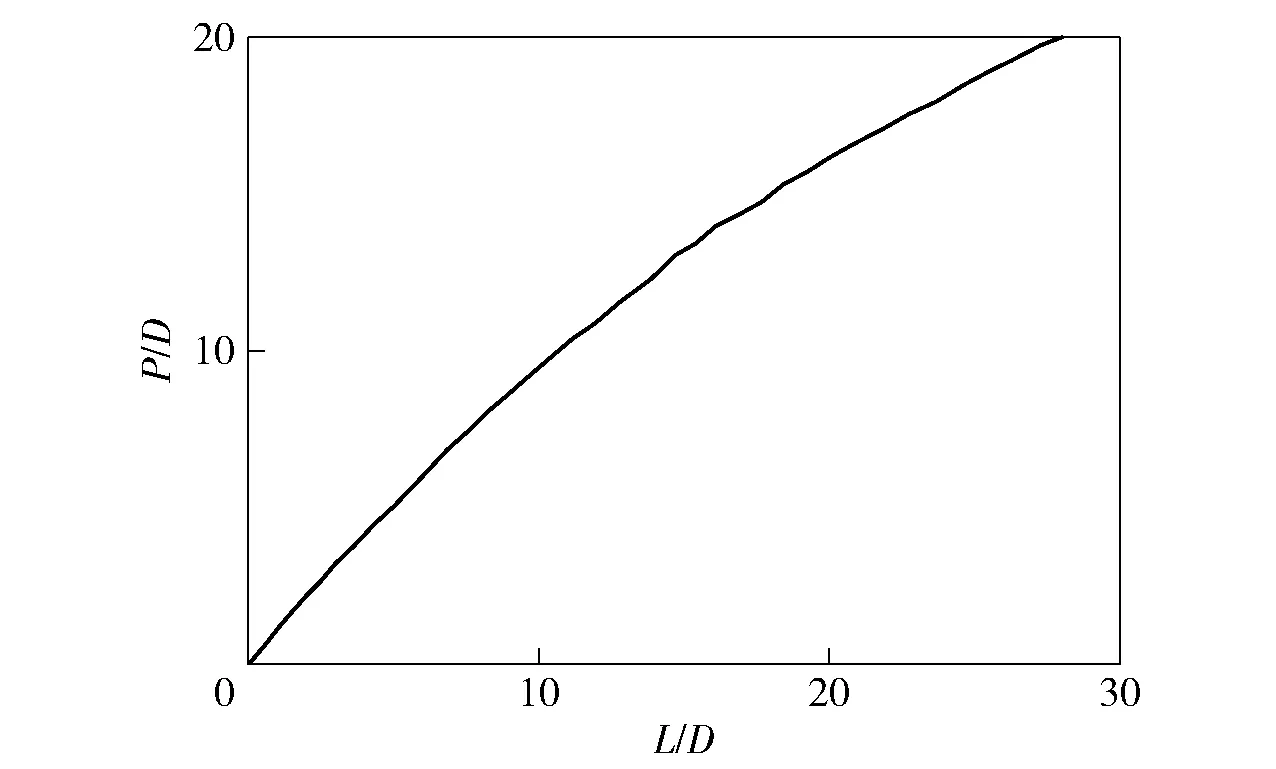
图11 长径比效应Fig.11 Effect of L/D
经过拟合曲线,将长径比效应表述为
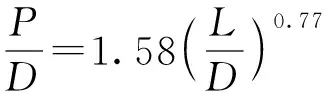
(3)
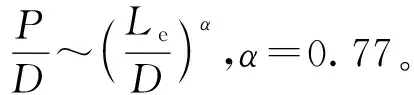
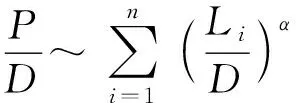
(4)
式中:为总分段数,这里为5;为分段杆各段长度。均匀分段杆侵彻总深度可以写为
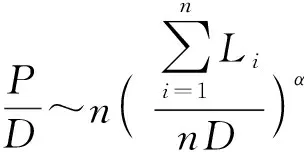
(5)
根据广义二项式定理可证以下不等式成立:
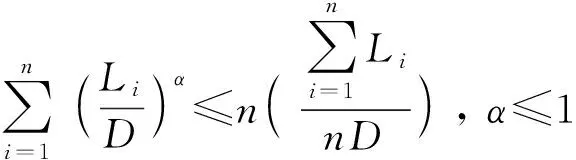
(6)
由此可知,固定分段杆弹直径和总有效长度时,均匀分段时侵彻总深度最大;而等差配置或者等比配置分段杆长度均会偏离最大点,使总体侵彻深度减小。
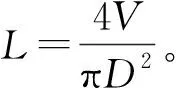
~(1-3)
(7)
由于=077,即1-3<0,在固定各段体积时,侵彻深度将随着直径的减小而增大。因此可以得出结论:在弹体总体积或总质量一定时,直径越小,长径比越小,总侵彻深度越大。
因此,基于上述结论即可构造直径梯度变化的分段杆弹。该分段杆弹在靶板法向方向上各段体积相等,直径逐渐增大,长度逐渐减小,所配置的各段杆弹长度和直径如表3所示。沿着靶板法向方向上直径递减,保持各段体积不变。计算结果如图12所示。3 000 m/s的初速下侵彻半无限装甲钢靶最终深度为71 mm,比均匀分布长杆深度要大26,即直径梯度配置的分段杆优于长度梯度配置的分段杆弹。

表3 变直径梯度杆配置Table 3 Variable diameter gradient rod configuration
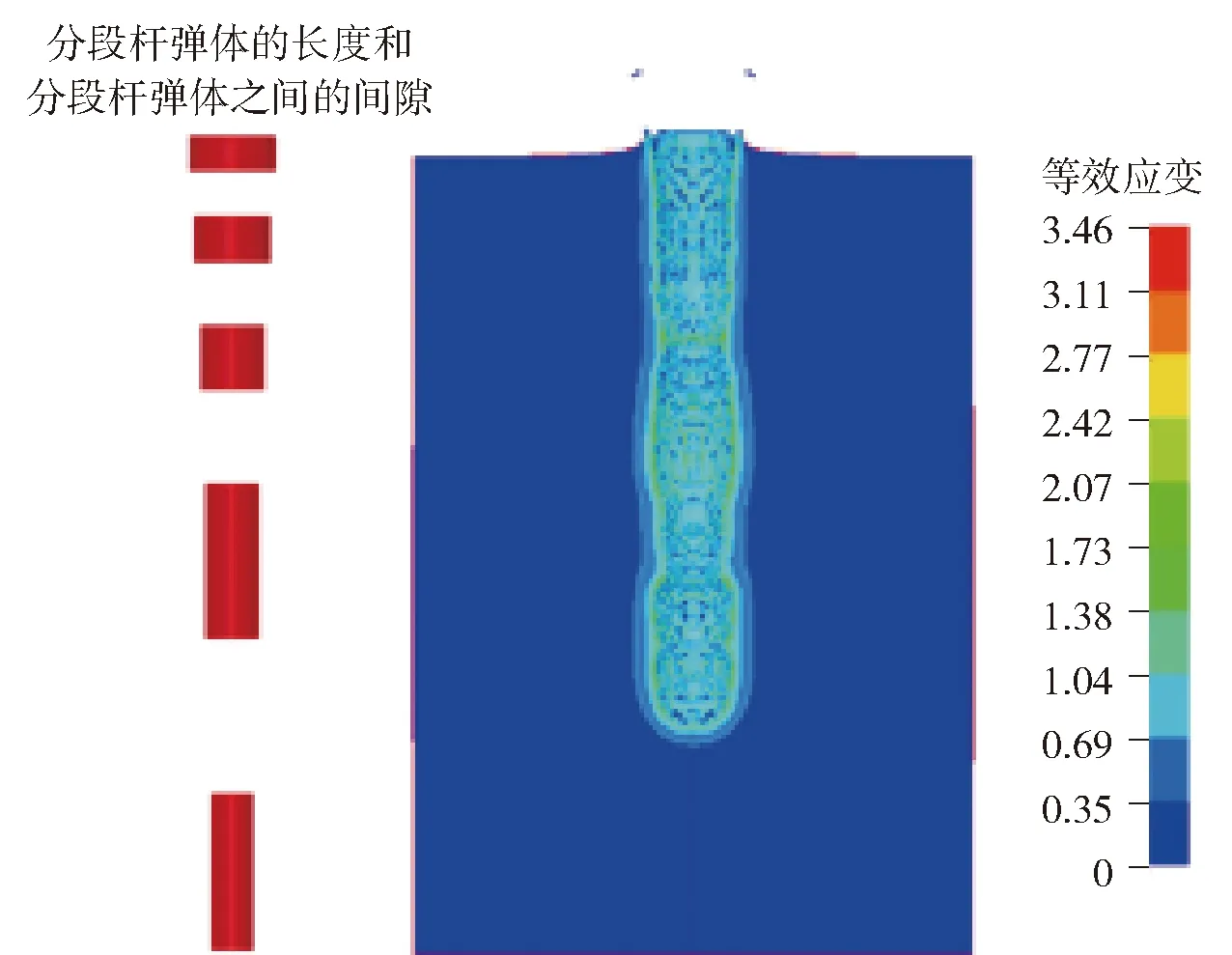
图12 变直径梯度杆及等效塑性应变云图Fig.12 Penetration of variable diameter gradient rod
4 结论
1) 本文利用LS-DYNA拉格朗日算法模拟了钨合金长杆弹侵彻半无限钢靶的实验,数值计算结果与实验结果较为一致,证明了数值模型的有效性。
2) 构造了5种等差梯度的分段杆弹,并进行了数值模拟。长度均匀相等的分段杆侵彻效率最高,侵彻深度最大;长度梯度变化杆,杆长等差值越大,侵深越小。
3) 阐述了长径比效应对等差梯度配置的分段杆弹侵彻深度的分段杆弹的影响规律,理论上证明了变直径和变长径比分段杆的可行性,并数值模拟进行了分析验证,为分段杆弹的优化设计提供了依据。
