基于GCI融合的分布式雷达抗欺骗干扰算法
2022-10-11朱永锋
朱永锋,达 凯,杨 烨
(国防科技大学 ATR重点实验室,长沙 410073)
0 引 言
有源欺骗干扰利用电子干扰设备生成假目标信息并作用于雷达检测与跟踪系统,使得雷达对真实目标的状态做出错误的检测及跟踪,这对情报搜集和军事打击造成了严重的影响。目前单站雷达抗欺骗干扰主要通过发射波形分集、 极化信息等技术降低干扰效果,或者通过区分干扰和真实目标在信号或数据维度上的差异来剔除假目标。但单站雷达包含的信息有限,能够达到的抗干扰效果也有限。随着传感器网络的发展,越来越多的雷达系统多站化、 网络化。多站雷达从不同角度利用不同体制的信号来观测目标,其相比于单站雷达,不仅在获取信息能力上更为突出,抗干扰能力也更强。通过多站雷达信息融合进行抗欺骗干扰的技术也是目前研究的重点方向之一。
根据融合抗欺骗干扰处理的数据不同,可以将其分为数据级融合抗欺骗干扰和信号级融合抗欺骗干扰。在数据级融合抗欺骗干扰方面,文献[9]提出了基于双基地雷达系统的有源欺骗假目标识别算法,利用统计判决构建了马氏距离检验量来辨别真假目标; 文献[10]提出了基于同源量测融合的抗欺骗干扰目标跟踪算法,在抗干扰部分设计自适应门限来减少输入假目标个数,之后在目标跟踪部分根据航迹优先级进行航迹关联以实现多目标跟踪; 在此基础上,文献[11]利用关联检验的方法保留了真实航迹,并通过数据融合提高了跟踪精度; 文献[12]基于多元统计分析理论,构造了量测误差的样本向量,利用似然比检验方法实现了对雷达网络中的假目标航迹的准确鉴别。在信号级融合抗欺骗干扰方面,文献[13]基于长基线条件下真实目标回波的各向异性和虚假目标回波的各向同性,提出了一种自适应门限真假目标鉴别方法; 文献[14]提出了基于聚类分析的抗干扰算法,在回波幅度比构建的特征空间中,通过聚类分析实现对假目标的鉴别。
总体来看,数据级融合抗欺骗干扰的主要方法是利用有源假目标在不同雷达上形成的量测不一致这一特点,设计量测聚类、 航迹关联等方法将其与真实目标区分开来。但是,当前的数据级融合方法主要针对集中式网络,难以应用于分布式网络。信号级融合与数据级融合相比,其融合级别更底层,包含的信息更多,潜在的抗干扰能力也更强,但雷达信号级融合十分复杂,其底层波形的设计运用和统计量构建难度大,也是未来研究的重要方向之一。
本文提出了一种基于数据级融合的分布式抗有源欺骗干扰方法。首先,利用集势概率假设密度(Cardinalized Probability Hypothesis Density, CPHD)滤波器同时跟踪真实目标与干扰假目标。与其他随机集滤波器相比,CPHD滤波器比概率假设密度(Probability Hypothesis Density, PHD)滤波器的目标估计性能更好,比多伯努利滤波器在分布式融合中的闭合性更好。然后,在不同传感器之间采用广义协方差交叉(Generalized Covariance Intersection, GCI)融合。对于干扰机生成的非协同假目标,根据GCI融合的迫零性质,假目标将被当作虚警抑制掉,而真实目标则通过融合得到增强。对于协同假目标,在雷达网络中增加处于被动工作模式的雷达,以破坏干扰机对整个网络的干扰。最后,通过一致性算法迭代,使雷达网络对目标的估计达到全局一致,实现对协同假目标的有效鉴别。
1 协同和非协同假目标
干扰机进行欺骗干扰的工作流程: 发现并捕获敌方雷达信号,分析信号并获取雷达工作参数,调制假目标信号并向外转发。目前常见的假目标欺骗干扰类型有基于时延调制生成的距离欺骗干扰、 基于幅度-相位调制生成的角度欺骗干扰、 基于频率调制生成的速度欺骗干扰以及以上几种联合调制产生的复合欺骗干扰等。
综上可知,准确获取雷达关键参数是成功实施欺骗干扰的前提条件。在分布式雷达网络中,对于真实目标,不同雷达的量测转换到公共坐标系下呈现出量测的一致性,考虑到量测误差的存在,其位置相对“集中”。
对于欺骗干扰,当干扰机无法获取所有雷达的相对位置及工作参数时,其转发的干扰是互相独立的,即对于不同雷达产生的假目标量测,将其统一转换到公共坐标系时呈现出量测的不一致性,其位置相对“分散”,此类假目标没有考虑到组网雷达协同探测的特性,称为非协同假目标。若干扰方能够提前获知整个网络的拓扑结构和各雷达参数,且干扰机性能较强,拥有充足的通道能够同时对所有雷达实施干扰,此时转发产生的假目标表现出真实目标的特性,即具有空间位置的一致性。此类假目标是干扰机针对各雷达协同欺骗产生,称为协同假目标。
以距离欺骗干扰为例,如图1所示。非协同与协同假目标的一个重要区别是,前者对来自于各个雷达站点的量测转化至公共坐标系下是不一致的,而后者则是一致的。
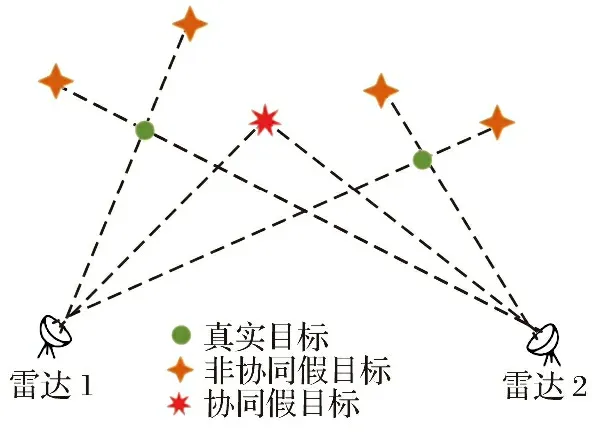
图1 非协同与协同假目标
2 CPHD滤波器的分布式GCI融合
2.1 CPHD滤波器
随机有限集(Random Finite Set, RFS)是一个元素互异、 无序,且数目可变的有限集合,其可以很自然地表征多目标过程中的虚警、 漏检、 目标新生以及消亡。近年来,基于RFS的多目标跟踪滤波器由于实现较为简单且性能优异,正受到越来越多的关注。
CPHD滤波器是随机集滤波器中的一种,其将先验和预测的多目标RFS建模为独立同分布群(Independent and Identically Distributed Cluster, IIDC)过程,并同时传递目标的势分布和强度函数。IIDC随机集的多目标密度和概率假设密度分别为
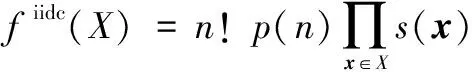
(1)
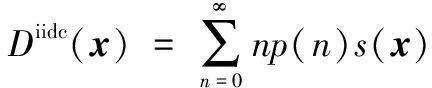
(2)
式中:()表示势分布;()表示单目标空间密度。CPHD滤波器的具体表达及实现可参见文献[15-16]。与最早提出的PHD滤波器相比,CPHD滤波器不仅迭代传递多目标状态集合的强度函数,同时迭代传递集合的势分布,在强漏检和虚警场景下,可以更准确地估计目标数量。假定场景下目标数目为,量测数目为,PHD滤波器计算复杂度为(),CPHD滤波器计算复杂度为()。可以看出,CPHD滤波器以计算复杂性为代价,获得了更优的跟踪性能。
2.2 分布式GCI融合
GCI融合是协方差交叉(Covariance Intersection, CI)融合向非线性、 非高斯方向的扩展。其在融合时可以避免融合节点间共同信息的重复计算,因此对网络的拓扑结构没有特殊要求,被广泛应用于分布式融合中。假定融合来自传感器∈N 的后验多目标概率分布(),GCI融合计算为
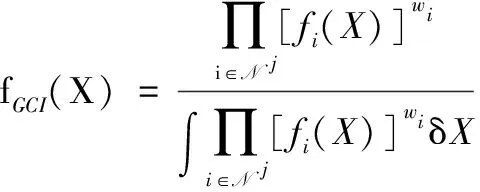
(3)
式中:表示指向传感器的多目标密度权重,并且∑∈N =1。
(4)
其中:
(5)
(6)
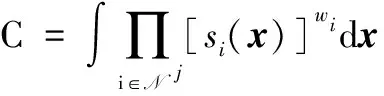
(7)
由上可知,融合后的单目标概率密度()是各节点概率密度()的加权几何均值,融合后的势分布()则较为复杂,与各节点概率密度()和势分布()均相关。
由式(4)可知,融合后的结果仍然存在复杂的积分计算,因此需要采用数值近似的方法进行计算,本文选取基于高斯混合(Gaussian Mixture, GM)实现方法。GM数值计算将目标的密度函数用一组加权的高斯分量近似表示,与序贯蒙特卡洛(Sequential Monte Carlo, SMC)方法相比,无需进行大量复杂的粒子变换,计算量大大降低。关于CPHD滤波器GCI融合的高斯混合具体实现方法,可参见文献[21]。此外,针对雷达量测的非线性问题,可将无迹卡尔曼滤波器(Unscented Kalman Filter)集成至CPHD滤波器的更新步骤,具体实现步骤可参见文献[16,22]。
3 基于GCI融合的抗欺骗干扰算法
3.1 GCI融合抗欺骗干扰原理
本节证明了GCI融合具有类似于密度近似中-收敛的迫零性质,并提出利用该性质抑制欺骗干扰。
单传感器下的迫零性质表示: 在状态空间中,假设()为一给定的已知分布,根据变分法则得到其近似分布(),对于∀∈,若()=0,则()=0。简而言之,迫零性质会强制近似分布()在源分布()零点处的值置零。
在多传感器多目标跟踪领域,融合是在已知一系列多目标概率分布前提下,求解近似多目标概率分布,故可将迫零性质引入多目标融合领域。假定表示状态空间X所有有限子集的集合,对于节点,融合多目标概率分布(),∈N 得到分布(),则多传感器多目标跟踪领域的迫零性质定义如下:
∀∈,若∃∈N且()=0,则()=0。
根据定义以及GCI融合公式可知,GCI融合具有迫零性质。
使用GCI融合密度()(∈N),得到()。对于任意,若∃∈N使得()=0,则()=0。

GCI迫零性质表明,没有被雷达检测到的目标将被融合结果舍弃,即在任意融合中漏检的目标将不会包含在GCI最终融合结果中。与此同时,所有雷达的本地检测中存在的虚警同样也会被消除,原因在于虚警是随机产生的,其往往位于各个雷达节点检测区域的不同位置,融合时同样会被消除。对于根据迫零性质被置零的目标,其概率质量将会转移到各个雷达均能够检测到的目标估计当中,会使剩余目标融合后的概率质量得到进一步提高,呈现出“尖峰”状,从而达到比融合前更好的检测效果。
3.2 GCI融合抗欺骗干扰算法设计
对于非协同假目标,其位置参数统一转换到公共坐标系时呈现出量测的不一致性,这类似于雷达检测中的虚警,可通过GCI融合的方法将其置零; 对于协同假目标,其仅产生于主动雷达的视场中,而处于被动工作模式下的雷达不主动对外辐射射频信号,无法被干扰机捕获、 调制、 转发,故可采取添加处于被动工作模式雷达的方法,使得假目标位置信息经由被动工作模式下雷达剔除。综上,可利用基于GCI融合的方法消除假目标。
图2利用仿真验证了以上结论。为了易于理解和方便讨论,仿真中对目标的状态估计形式做了简化处理。由图可知,主动工作模式雷达间融合只能抑制非协同假目标,而主/被动工作模式下的雷达融合可同时抑制协同和非协同假目标。此外,融合使得目标的估计分布更加集中,达到了更好的跟踪效果。
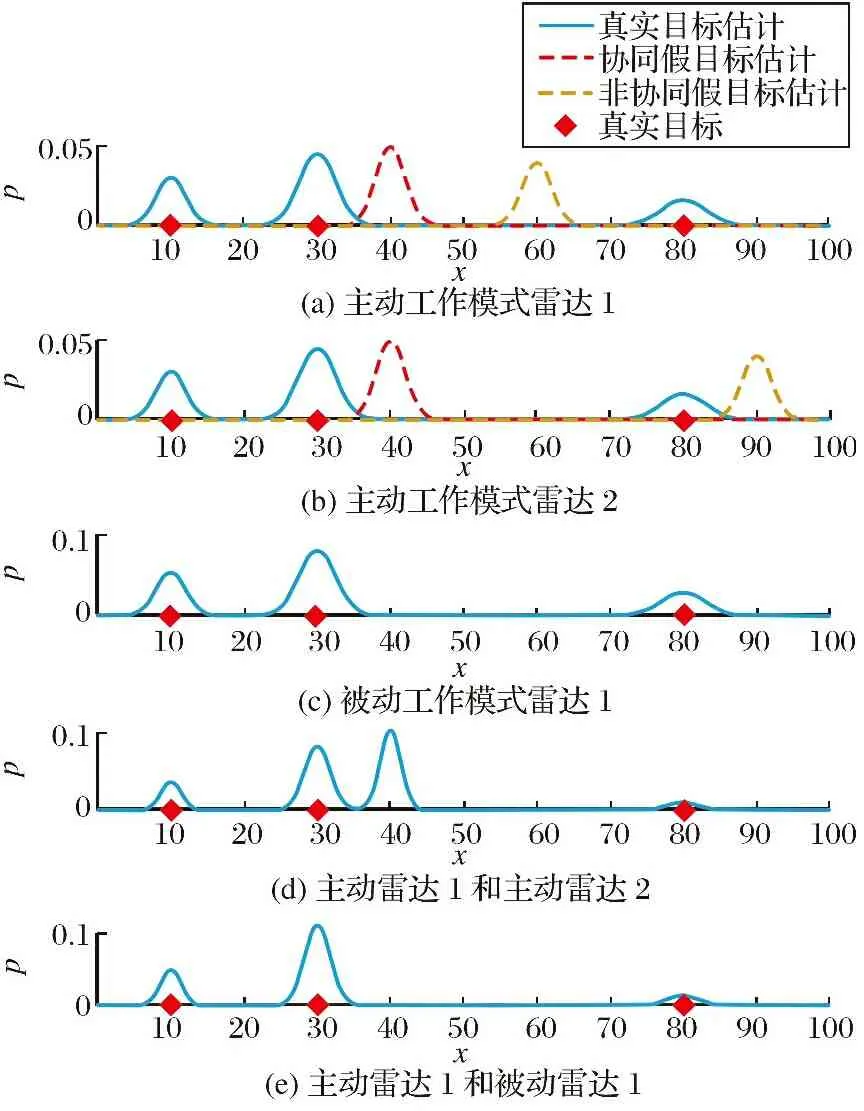
图2 GCI融合抗假目标示意图
在对抗协同假目标时,为了将被动雷达的鉴假信息传递给所有主动雷达,需要采用一致性算法。一致性GCI融合在邻居节点间迭代使用GCI融合,将整个网络信息(包括多目标状态、 真假目标标记)不断传播,并最终达成全局一致性,其收敛性已由文献[23]证明。根据GCI融合的迫零性质,非协同假目标在迭代前通过多个主动雷达融合即被抑制,而协同假目标将随着被动雷达信息的传递而逐步被抑制。
综上,非协同和协同假目标同时存在情况下的抗欺骗干扰多目标跟踪算法如图3所示。

1.输入: k时刻各雷达本地所有的目标量测值: {Zk, i}Ni=1; k-1时刻各雷达融合后真实目标的强度函数和势分布: {DGCI, k-1, i(x); pGCI, k-1, i(n)}Ni=1; 2. 步骤1: 各雷达本地执行高斯混合CPHD滤波器; 3. for雷达i=1, 2, …, N do4. 求解本地滤波后的强度函数Dk, i(x)和势分布pk, i(n); 5. end for; 6. 步骤2: 各雷达进行GCI融合, 并进行一致性迭代; 7. for一致性迭代次数l=1, 2, …, L do; 8. 传感器信息交换; 将接收到的信息转换至本地坐标系下; 9. for雷达i=1, 2, …, N do; 10. 执行CPHD滤波器的GCI融合算法; 11. end for; 12. end for; 13. 输出: k时刻各雷达融合后目标的强度函数和势分布为 {DGCI, k, i(x); pGCI, k, i(n)}Ni=1。
4 仿真分析
4.1 参数设置
考虑在2 500 m×2 500 m的二维平面中跟踪3个在场景中做小角度转弯运动的目标。分布式雷达网络由6个雷达站点构成,包括4部主动雷达和2部主/被动模式可自由切换的雷达,在仿真中这2部雷达工作于被动模式。分布式雷达网络的拓扑结构如图4所示,黄色虚线表示雷达间的通信链路。各雷达具体参数如表1所示。
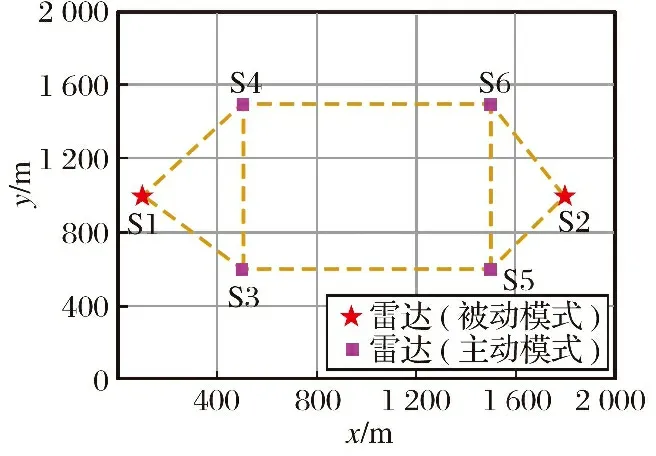
图4 分布式雷达网络拓扑结构
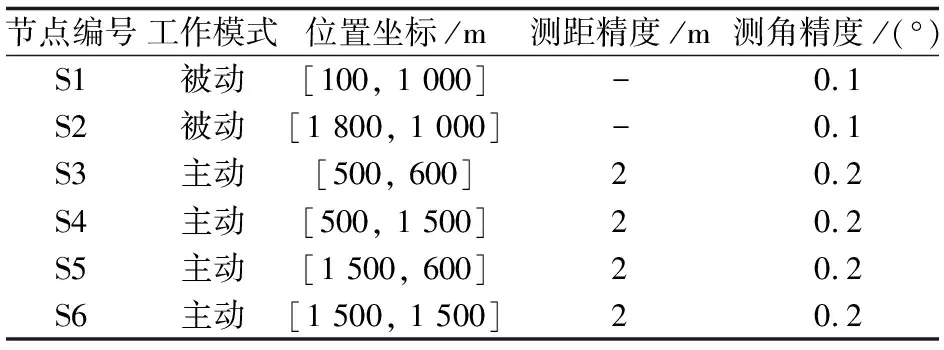
表1 雷达站点参数
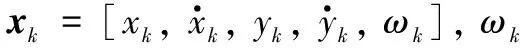
=-1+[-1,, ]
(8)
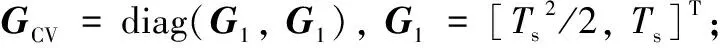
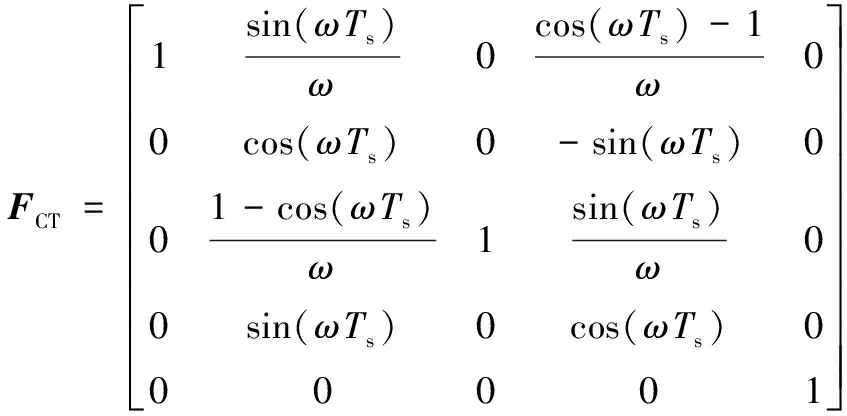
(9)
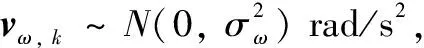
图5展示了该仿真场景下的真实目标与假目标轨迹。图中黑色细实线点迹表示真实目标轨迹,红色点迹表示主动工作模式雷达S3视角下的非协同假目标轨迹,蓝色点迹为协同假目标点迹。点迹上的空心圆圈标记表示各目标起点,空心三角标记表示各目标终点。各目标运动参数如表2所示。
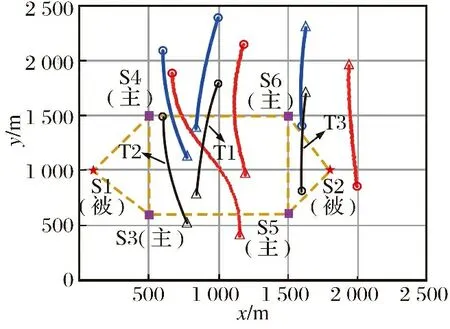
图5 目标轨迹
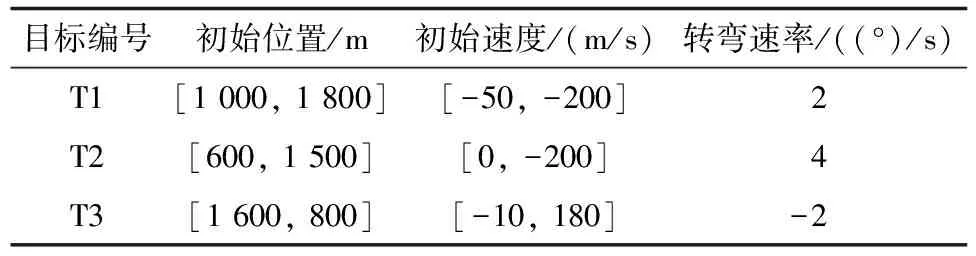
表2 目标参数
受欺骗干扰影响,仿真中假设每个主动雷达在测得真实目标的位置信息外,同时会生成一组与真实目标相关的协同假目标和非协同假目标。具体生成方式: 协同假目标在每个真实目标的正北方向500 m处生成,非协同假目标在每个雷达的真实目标量测角度维增加1°、 距离维增加300 m处生成。
其他参数的具体设定: 目标存活概率为0.99,所有雷达对目标的检测概率均为0.95,主动雷达对干扰的检测概率为1。新生目标的强度函数以均匀分布的高斯混合形式布满整个仿真场景。一致性算法中的迭代次数为3,蒙特卡洛仿真次数为100。
4.2 实验结果
目前研究中尚缺乏对多目标跟踪下的分布式抗欺骗干扰算法,因此实验仅分析本文所提出算法的欺骗干扰抑制能力以及多目标跟踪的能力。
图6展示了利用本文算法估计目标数目的情况。由图可知,本文所提算法可以抑制欺骗干扰,除在滤波初始阶段因航迹生成存在抖动外,其余时刻估计目标数目均与真实目标数目基本相符。
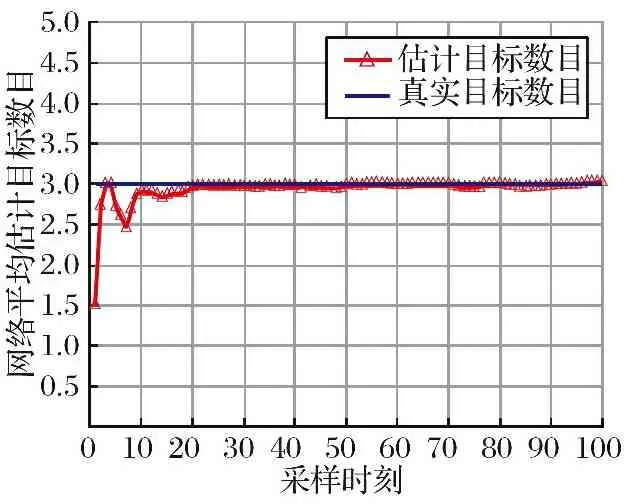
图6 平均估计目标数目
图7展示了蒙特卡洛仿真后的平均最优子模式分配(Optimal Subpattern Assignment, OSPA)误差。仿真中设定OSPA误差的截止参数=600 m,距离敏感参数=2。不难发现,除在航迹生成的初始阶段误差水平较高外,其余时刻均稳定在较低水平,远低于截止参数,说明本文算法在成功剔除假目标的同时具有较高的跟踪精度。
图8展示了单次仿真中雷达节点S3跟踪的目标轨迹。由图可知,除了在航迹生成阶段估值不稳定,以及极少数时刻的跟踪结果出现野值外,绝大多数时刻的估计值均与对应目标轨迹相吻合,输出的融合结果说明其跟踪的为真实目标,而不是干扰,这进一步验证了算法的正确性和有效性。

图7 平均OSPA误差
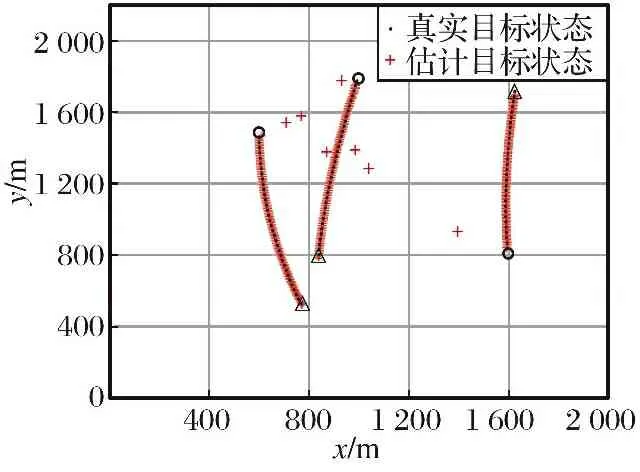
图8 多目标估计状态
5 结 束 语
本文针对分布式雷达网络,提出了GCI融合抗有源欺骗干扰多目标跟踪算法。仿真结果表明,在多目标场景下,所提算法在有效抑制非协同和协同有源假目标的同时,能够保持对目标数量和状态的精确估计。目前,文章仅利用数据级融合方法,对分布式雷达网络抗有源假目标问题进行了研究。下一步计划结合信号级融合方法,进一步提高分布式雷达网络的抗干扰能力。
