磁谐振无线电能传输系统优化设计方法

王 猩

(佳木斯大学 信息电子技术学院, 黑龙江 佳木斯 154007)

0 引 言

随着中国智能电网的深入化、成熟化发展，高压输电线路在线监测设备得以广泛应用，然而在线监测设备的供电方式成为在线监测设备亟待解决的重要问题之一。由于高压输电线路的自身绝缘条件和所处地理环境的限制，无法直接从输电线路上将其电能输送给在线监测设备，并且高压输电线路所处的地理环境通常十分恶劣，采用电池供电、小型风机供电以及太阳能供电等方式并不可靠。因此,为了保障在线监测设备能够长期在野外安全稳定运行，采用无线电能传输(wireless power transfer, WPT)作为在线监测设备的供电电源显现出了其独特的优越性。由于磁耦合谐振式无线电能传输具有传输效率高、传输功率大、传输距离远且对周围环境影响较小的优点，近年来在电动汽车、医疗、家用电器等领域得到了广泛关注和使用[1]。

自2007年MIT在电磁共振原理上进行突破，并成功在2 m以外点亮了一只60 W的灯泡，才逐渐打破了电磁感应原理对以往多数科学家的束缚，为大功率、中距离无线电能传输技术的发展提供了一个新思路[2]。而磁耦合谐振式无线电能传输系统参数的优化对于提高系统的传输能量和效率具有重要意义。文献[3]采用控制变量法讨论了系统接收线圈匝数和半径对传输功率和效率的影响关系，从而寻求接收线圈匝数和半径的最优值。文献[4]通过实验验证了线圈半径、线径、角频率等因素对系统功率和效率的影响，并解决了线圈多参数设计的顺序问题，为线圈的优化设计提供了指导。文献[5]通过理论分析和实验验证，得出线圈参数对于系统传输功率和传输效率的影响度为N>r>s>a，然而由于线圈参数之间的互相影响关系，仅根据影响顺序采用控制变量法对系统进行优化设计并不能得到最优参数。文献[6]采用遗传算法分析了系统频率和传输距离对系统传输功率的影响关系，并验证了遗传算法运用于无线电能传输系统优化设计的有效性。这是对于系统整体优化的一个突破，但是事实上，两线圈的参数保持一致时未必能得到最优值，因此需要把发射和接收侧的线圈都作为变量分析。

针对110 kV输电线路在线监测设备的无线供能电源，该文提出采用自由参数扫描法对系统线圈进行优化设计，考虑系统谐振频率、发射线圈匝数、发射线圈半径、接收线圈匝数、接收线圈半径以及线径等6个参数对系统传输功率和传输效率的影响，设计出具有较高传输效率的无线电能传输系统。

1 磁谐振WPT系统模型

目前对磁耦合谐振式无线电能传输系统进行分析的模型主要有耦合模理论、互感等效电路以及二端口网络这3种分析模型[7]。虽然在特定条件下，通常可以将这3种求解模型进行相互转化等效，但是相对于耦合模理论和二端口网络，互感等效电路简洁明了、应用广泛，并且直接体现了系统参数与传输功率和传输效率的关系，因此该文采用互感等效电路模型来分析影响传输功率和传输效率的主要因素[7]。无线电能传输原理图和等效电路图如图1所示。

图1中：Us为高频交流电源(一般为几百kHz～几MHz)，Rs为发射端电源等效电阻，L1、L2分别为发射端线圈和接收端线圈等效电感，R1、R2分别为发射端线圈和接收端线圈等效电阻，RL为负载电阻，C1、C2分别为发射线圈和接收线圈的补偿电容。选择串联结构作为补偿拓扑，由补偿电容和线圈串联组成，并与线圈等效电感发生谐振，从而实现电能传输。

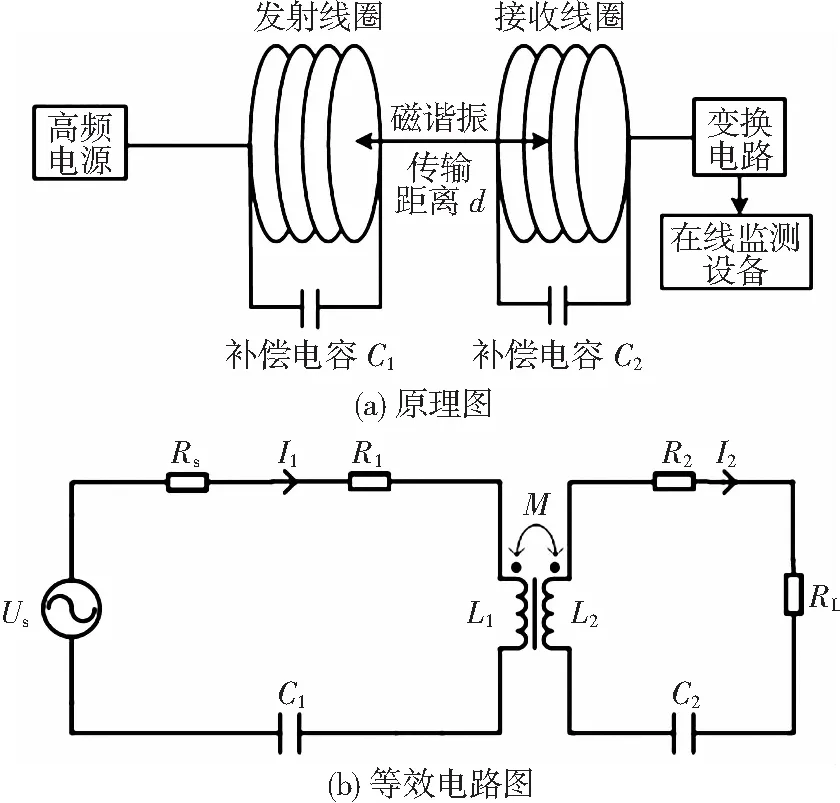
图1 无线电能传输原理图和等效电路图Fig.1 Schematic diagram and equivalent circuit diagram of wireless power transmission

由系统的等效电路可知，根据基尔霍夫电压定律(KVL)可得

(1)

为减少电路无功损耗，增大传输效率，应使发射线圈和接收线圈均发生谐振，即

(2)

简化式(1)得

(3)

联立解得发射回路和接收回路的电流分别为

(4)

根据传输功率和传输效率的定义，可求得系统传输功率P和传输效率η与系统各参数之间的数学关系表达式为

(5)

由式(5)可知，系统的传输功率和传输效率不仅与线圈之间的互感M有关，还与线圈等效电阻R1、R2有关，也就是和线圈的各个电参数有关，故传输功率和传输效率为各电参量的函数，即

(6)

对于线圈中的等效电阻R1、R2，由高频时线圈的损耗电阻Rohm和辐射电阻Rrad组成。然而，辐射电阻Rrad一般在10-4数量级上, 所以相对于损耗电阻来说可忽略不计。而螺旋线圈的损耗电阻可通过下式得出：

(7)

式中：r为线圈半径,m；a为铜管截面直径，m;a′为线圈导线的有效截面积半径,m；N为线圈匝数；lc为线圈长度，m;σ为导体电导率,S/m，对于该文所选择的铜线圈，导体的电导率为5.8×107S/m。

对于2个线圈之间的互感，空心螺旋线圈间的互感可参考Neumann公式：

(8)

式：μ0为真空中的磁导率，取4π×10-7H/m；N1、N2为两线圈匝数；l1，l2为线圈1与线圈2上的微小线元素；A为微小线元素dl1的坐标位置；B为微小线元素dl2的坐标位置。

对于相互平行且共轴的2个线圈而言，其互感的表达式为

(9)

式中：N1、N2分别为发射线圈和接收线圈的匝数；r1、r2分别为发射线圈和接收线圈的半径；μ0为真空中的磁导率，取4π×10-7H/m。θ、φ均为积分因子；d为两线圈间轴向距离。

对于线圈的等效电感和补偿电容，空心螺旋型线圈的自感以及补偿电容的表达式如下：

(10)

式中：L为线圈等效电感量;μH，D为线圈的直径,cm;ld为螺旋线圈轴向长度,cm;N为线圈匝数。其中线圈长度ld为

ld=a+(N-1)(w+a)

(11)

式中:w为线圈相邻两匝间的距离，该文所设计的系统中匝间距固定为5.5 m。

由式(7)～(10)可知，系统中的各电参数又可以表示为f、r1、r2、N1、N2、a′的函数，因此系统传输功率和传输效率也可以表示为f、r1、r2、N1、N2、a′的函数，即

(12)

2 系统单参数对传输功率和输出效率的影响

2.1 单参数影响分析

由效率和功率的函数关系式可知，线圈参数设计优化具有强耦合、多参数的特点，通常难以找到参数空间中的全局最优解。因此，这里首先将单个参数作为变量，分别讨论f、N1、N2、r1、r2和a′对传输功率和效率的影响关系。对照组参数:f=500 kHz，N1=N2=12，r1=r2=0.2 m，a′=3 mm。线圈各参数与传输功率、效率的关系如图2所示。

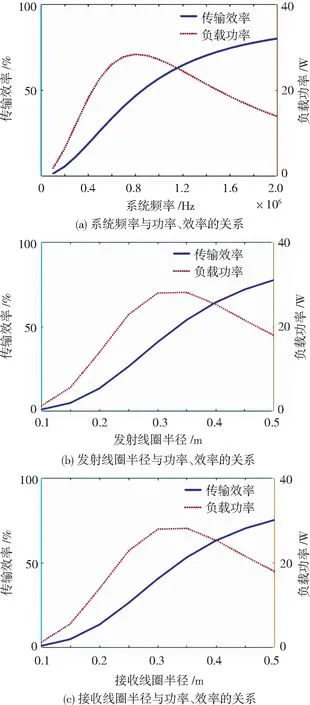
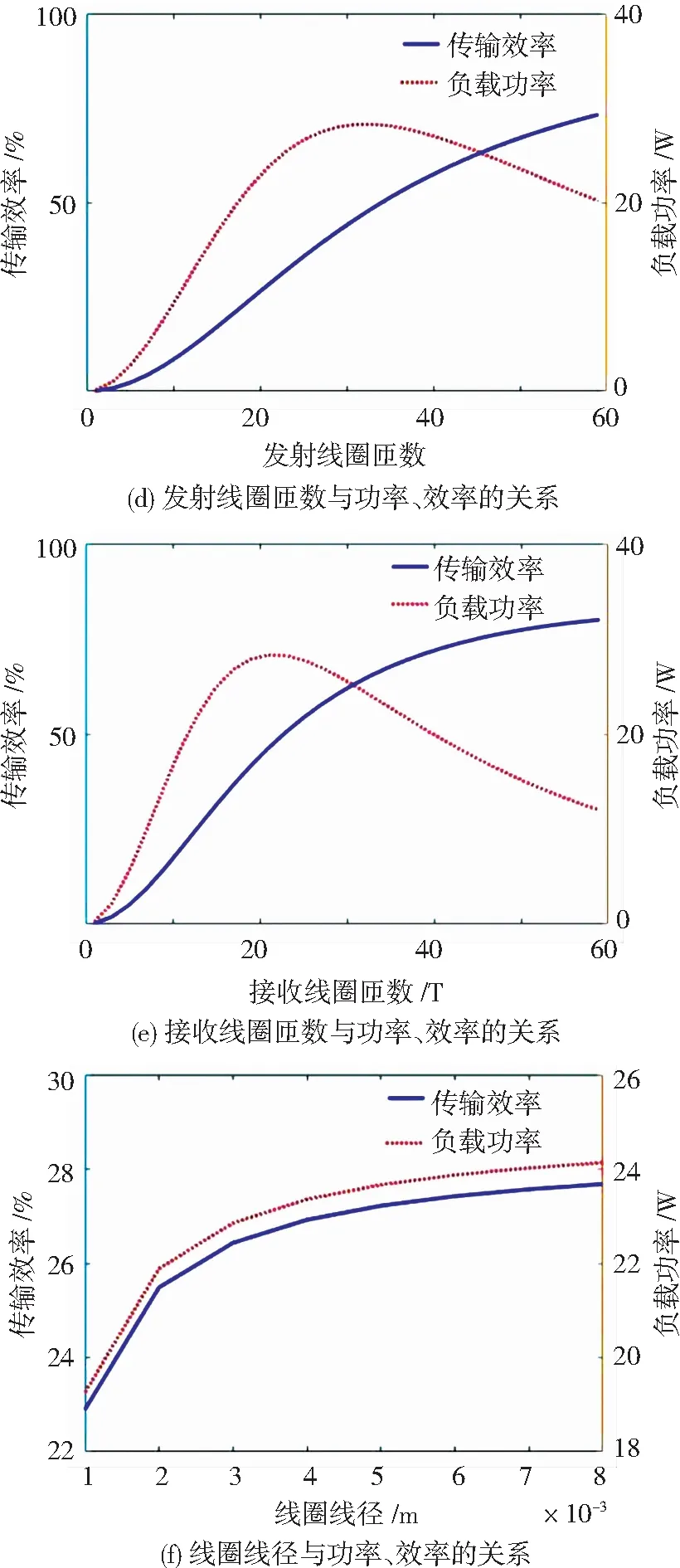
图2 线圈各参数与功率、效率的关系Fig.2 Relationship between coil parameters,power and efficiency

2.2 影响分析结果

通过讨论单参数对系统功率和效率的影响关系，可以得到以下结论：

1)根据纵坐标的变化可知，系统各参数对系统效率和功率的影响大小是不同的。因此，在进行线圈参数优化时，按照一定的优化顺序才能保证参数优化的合理性。

2)从图2(a)中可以看到，系统功率随频率的增大而不断增大。当我们以传输功率为优化目标时，则需要增大系统的谐振频率来增大传输功率。然而，现实中由于各种因素的限制，系统频率不可能无限增大，所以在参数优化时，需要对系统频率进行约束。此外，由于应用场合的不同，线圈的大小也必须进行限制。

3)系统的各参数之间存在相互作用，系统中某一个参数发生变化，会对系统另一参数的优化产生影响，所以采用控制变量法来对多参数的系统进行优化设计不能保证结果的精确性。

因此，提出采用自由参数扫描法对系统参数进行整体性优化，不仅可以消除优化顺序对结果的影响，还可以通过约束条件，对系统的参数进行约束，保证优化结果的合理性和可行性。

3 基于自由参数扫描法的优化设计方法

3.1 优化设计流程以及实现方法

基于自由参数扫描法优化设计流程如图3所示。

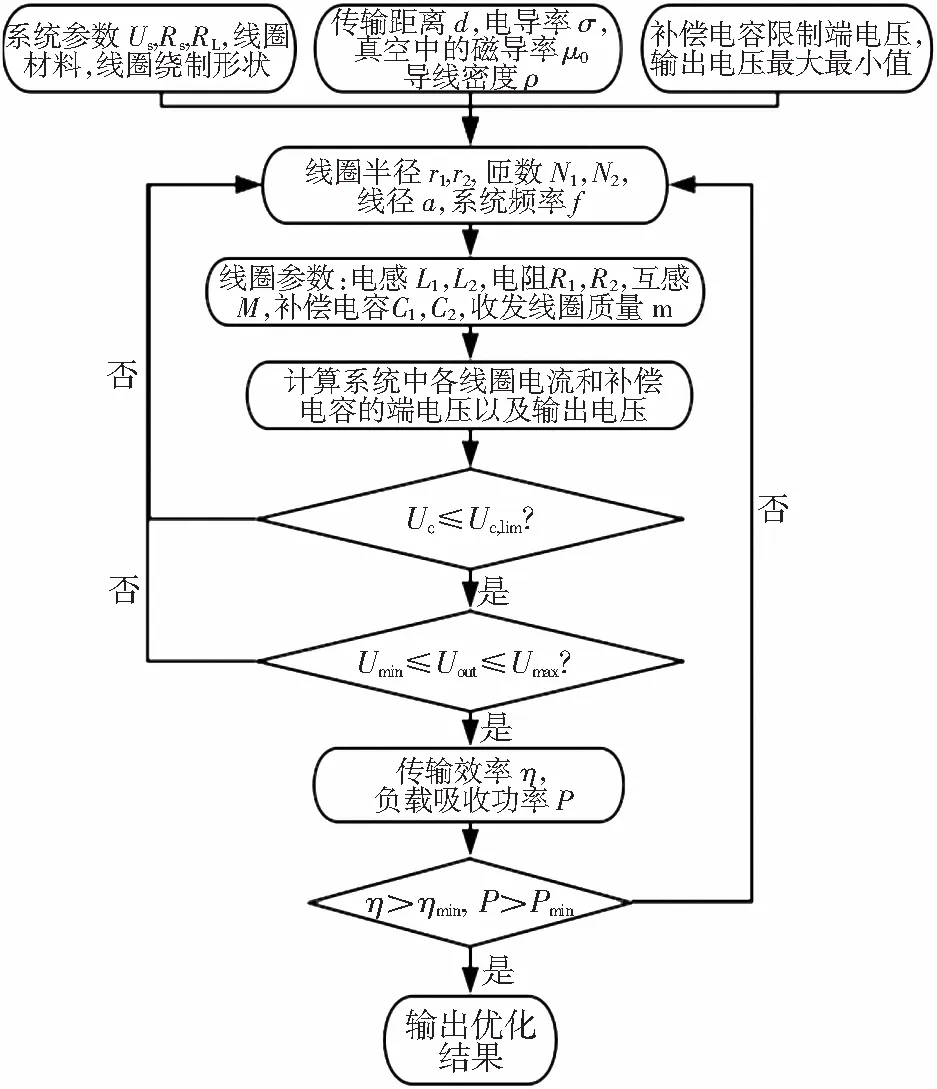
图3 系统优化设计流程Fig.3 System optimization design process

自由参数扫描法的基本思想是：在设定的自由参数范围内，根据各个约束条件对所有可能的情况逐一验证，直到所有的情况验证完毕。若某个情况验证符合约束条件，则此情况为该优化设计的一个解。反之，不符合约束条件的情况则舍弃。最终将所有满足条件的解输出，绘制出优化解的帕累托图。优化的目标为传输功率和传输效率，所以将式(5)作为目标函数。在一个系统里，一般电源幅值是已知的，负载阻抗通常也不会变化，并且针对110 kV输电线路在线监测设备的无线供电电源进行优化设计，而110 kV输电线路与杆塔间的安全绝缘距离为1.022 m，也就是说线圈间的传输距离至少为1.022 m，所以该文将传输距离设定为1.1 m。这里假设电源Us=35 V，等效内阻Rs=10 Ω，负载为纯阻性负载RL=10 Ω。那么需要进行优化设计的系统参数有谐振频率f，发射线圈半径r1和匝数N1，接收线圈半径r2和匝数N2,以及线圈的线径a′。并且，还需要同时对输出电压幅值、补偿电容两端电压等进行约束。

3.1.1 系统固定参数

系统的固定参数包括：电源电压幅值Us,电源等效内阻Rs，负载等效电阻RL，传输距离d，铜的电导率σ=5.8×107S/m，导线密度ρ=8.9×107kg/m3，以及真空中的磁导率μ0=4π×10-7H/m等。

3.1.2 自由参数

自由参数包括：谐振频率f，发射线圈半径r1和匝数N1，接收线圈半径r2和匝数N2，以及线圈的线径a′。对这6个自由参数进行扫描取值，可以得到多组满足约束条件和目标函数的设计方案。自由参数的取值范围必须在符合实际的范围以内，例如，系统谐振频率f受到系统各器件的限制(不能超过开关器件的最大工作频率)，以及线圈的大小受到输电线路空间位置的约束等。因此，优化参数的求解范围如表1所示。

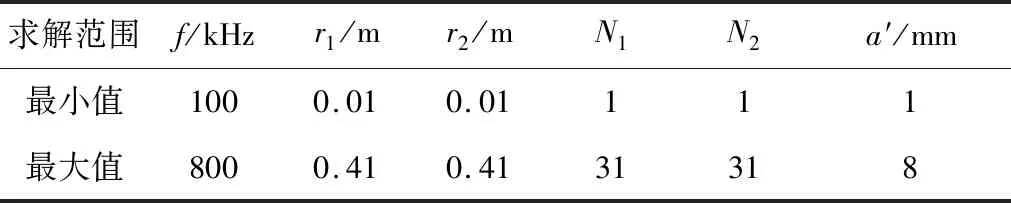
表1 优化参数的求解范围Table 1 Solution range of optimization parameters

3.1.3 约束条件

在磁耦合谐振式无线电能传输系统优化设计过程中，首先系统的输出功率和输出电压应该满足负载正常工作下的用电需求。此外还需要对系统的传输效率进行约束，在输出功率一定的情况下，传输效率太低，会产生大量损耗造成不必要的损耗。因此，主要的电气特性约束指标有3个，如下式所示：

(13)

输出电压Uout不能小于最低限定值，需要保证负载用电的电压需求，并且Uout也不能大于最大的限定值Umax，否则会超出用电负载的承受极限。传输效率也要大于最低约束，输出功率P要满足最低约束Plim。

磁耦合谐振式无线电能传输系统中除了输出电气特性的约束，还需要满足补偿电容两端电压的限制。在大功率的应用场合中补偿电容电压过高，会增加设计工程的难度，补偿电容的电压应参考实际所选择的电容型号的限制电压来进行约束。该文涉及的无线电能传输系统中采用的是串联结构作为补偿拓扑，有2个谐振电容，则他们两端的电压UC1和UC2分别为

(14)

3.2 优化结果

按照图3所示的优化设计流程，在约束范围内进行自由参数的扫描取值，获得满足约束条件的优化设计参数。图4为所得的各组优化参数的传输效率和输出功率情况，不同的点代表着不同的设计参数。

图4 传输效率与输出功率Fig.4 Transmission efficiency and output power

由图4可知，在实际的传输系统中，输出功率和传输效率不能够同时到达最大值。所以，在选择系统的优化设计参数时，应当根据现实情况来做出选择。当以系统的输出功率作为主要考虑因素时，则应在满足传输效率要求的同时，以最大输出功率为目的。反之，若以传输效率为主要考虑目标时，则应在满足输出功率的情况下，以传输效率最高作为参数选择的最终目标。

由图4可知，存在很多符合约束条件的设计方案，以传输效率作为主要考虑因素，因此在满足在线监测设备功率需求的条件下，使传输效率尽可能最大。选取其中1组设计方案进行验证，谐振频率f=300 kHz,发射线圈半径r1=0.39 m和匝数N1=25，接收线圈半径r2=0.41 m和匝数N2=17，线圈的线径a=5 mm。根据式(7)、(9)～(10)可计算出系统的各个电参数，发射线圈的等效电阻R1=0.279 Ω、等效电感L1=633.5 μH、补偿电容C1=444.2 pF，接收线圈的等效电阻R2=0.199 Ω、等效电感L2=364 μH、补偿电容C2=773.1 pF，以及线圈之间的互感M=11.6 μH。再将这些参数代入式(5)计算可以得到

(15)

可以看出，该设计方案的输出功率可达16.46 W，满足输电线路在线监测设备的功率用电需求，并且传输效率可达80.7%，可将发射端的大部分能量传输到接收端供负载消耗。

4 结 语

该文基于自由参数扫描法来综合考虑各影响因素，以系统传输功率和传输效率为目标函数，同时对系统各参数进行约束，最终得到符合优化要求的帕累托最优解。该文将所得到的帕累托最优解采用解析表达式进行计算，输出功率可达16.46 W，满足输电线路在线监测设备的功率用电需求，并且具有较高的传输效率，可达80.7%。这为磁耦合谐振式无线电能传输系统的优化设计提供一种有效的设计方法。