近断层地震动脉冲特性对设备-结构耦合隔震体系响应的影响＊

2022-10-10蒋金卫杜红凯赵鸣鹤

地震学报 2022年5期

韩淼蒋金卫杜红凯赵鸣鹤

（中国北京 100044 北京建筑大学北京未来城市设计高精尖创新中心）

引言

近年来，近断层地震动脉冲特性对结构的影响引起了国内外学者的广泛讨论.关于结构响应与脉冲特性的关系解释，主要表现在以下方面：① 与速度脉冲有关（Makris，Chang，2000；Lohet al，2002）；② 与速度脉冲时段内所发生的地面位移有关（Hallet al，1995）；③ 与加速度脉冲有关（Anderson，Bertero，1987；Vassiliou，Makris，2011）；④ 工程中用反应谱描述脉冲对结构的影响可保证一定精度，但规范谱不能很好地描述（胡聿贤，2006；李爽，谢礼立，2007）.

脉冲周期是近断层地震动脉冲特性的一个重要指标，很多学者根据速度脉冲来确定地震波的脉冲周期（Rodriguez-Marek，2000；Mavroeidis，Papageorgiou，2003；Bray，Rodriguez-Marek，2004；Shahi，Baker，2014）.因近断层地震动的脉冲具有长周期的特征，而隔震技术具有延长结构自振周期的特点，故许多学者对近断层脉冲型地震动作用下的隔震结构响应进行了大量研究（杨迪雄等，2005；李小军等，2018；潘毅等，2018）.

随着社会的发展和人们对生活环境需求的提高，结构中设备和仪器逐渐增多，在建筑总投资中的占比逐渐增加；建筑主体结构与其内部设备等非结构构件是耦合的结构整体，当设备质量较大时，两者的相互作用不应忽略.关于远场地震作用下，采用隔震技术的设备-结构耦合体系的动力响应研究已取得一定成果（李杰等，2003；韩淼，王亮，2005；国巍，李宏男，2008；Oropezaet al，2010）.而关于近断层地震作用下设备-结构耦合隔震体系动力响应的研究较少，尤其是关于近断层地震动脉冲特性对设备-结构耦合隔震体系动力响应影响的研究有待深入.

为此，本文拟采用有限元软件建立设备-结构耦合隔震体系模型，基于耦合隔震体系的时程响应与近断层地震动的速度脉冲和加速度脉冲的对应关系，分析脉冲周期和脉冲能量对结构响应的影响与脉冲周期和结构基本周期的比值的相关性以及脉冲对应加速度曲线的穿零次数对结构响应的影响，以期为设备-结构耦合隔震体系在不同近断层脉冲型地震作用下的响应差异提供分析方向.此外，还研究设备响应与脉冲特性和楼面时程的相关性，以期为近断层脉冲型地震作用下耦合隔震体系的设备响应预测提供参考.

1 结构分析模型

某五层钢框架结构，设防烈度Ⅷ度，场地类别Ⅱ类，设计地震分组第一组，框架层高3.6 m，纵、横向均为6跨，跨度7.2 m （图1）.由于受振动台台面尺寸的限制，开展振动台模型试验时，将实际结构简化为双向单跨原型结构并制作缩尺模型；为考虑受重力效应的影响，采用人工质量模型；几何相似比为1/4，弹性模量相似比为1/1，加速度相似比为1/1，质量相似比1/16，其它参数相似比列于表1.梁、柱均采用方钢管，钢材采用Q355钢，截面尺寸分别为 70 mm×70 mm×6 mm 和 100 mm×100 mm×5 mm.楼板采用 10 mm 钢板，第一至四层的配重为 2040 kg，第五层配重为 2 268 kg.

图1 五层钢框架结构Fig.1 Five-storey steel frame structure

表1 缩尺模型与原型的相似关系Table 1 Similarity relation of single-span model and prototype structure

双向单跨原型结构与其缩尺模型的前三阶自振周期，如表2所示；将缩尺模型的自振周期根据相似比1/2转换后与原型结构周期进行对比，误差＜3%，满足计算精度要求.

表2 原型结构和缩尺模型的前三阶自振周期Table 2 The first three natural vibration periods of prototype structure and single-span model

每根柱下安装一个橡胶隔震支座，支座直径150 mm，水平刚度为 0.25 kN/mm.缩尺模型如图2所示，其顶层耦合一个由四根长度400 mm的圆钢连接的设备，组成设备-结构耦合隔震体系；圆钢间距为250 mm，直径为12 mm，设备质量为200 kg，自振周期为 0.25 s.利用 Abaqus有限元软件进行建模，梁柱采用B32梁单元，楼板选用S4R5壳单元；耦合隔震体系的基本周期为0.85 s.

图2 有限元分析模型Fig.2 Finite element calculation model

2 地震波选取

从太平洋地震工程研究中心（Pacific Earthquake Engineering Research Center，缩写为 PEER）数据库选取50条具有脉冲特性的近断层地震波，序号按脉冲周期升序排列，列于表3.选取原则如下：

表3 本研究选取的 50 条近断层脉冲型地震波Table 3 The 50 near-fault pulse-like seismic waves selected for this study

1）根据国内外大多数学者公认的近断层地震动断层距的定义，选取断层距在20 km以内的地震波.

2）为突出近断层地震动异于远场地震动的强度特征，选择MW不小于5.5的地震波.

3）为突出近断层地震动的强地面运动特性，选择峰值加速度（peak ground acceleration，缩写为PGA）大于0.10g的地震波；

4）地震波是否具有脉冲以及脉冲周期数值根据PEER数据库确定（Baker，2007）.

为对比分析，从PEER数据库中选取50条无脉冲特性的近断层地震波，并按峰值位移（peak ground displacement，缩写为 PGD）升序排列.

3 设备-结构耦合隔震体系动力响应分析

将选取地震波的PGA调幅至0.07g，0.20g和0.40g，依次对应设防烈度Ⅷ度的小震、中震和大震的峰值加速度，分组输入到设备-结构耦合隔震体系模型，对耦合隔震体系进行动力分析，以研究近断层地震动的脉冲特性对设备-结构耦合隔震体系动力响应的影响.描述结构动力响应的物理量有加速度、速度、位移以及应力等；但工程中对结构响应的判断主要以位移为主，如弹性层间位移角、弹塑性层间位移角等，故本节主要以结构的位移响应为主要分析对象.

3.1 主体结构响应

PGA分别为0.07g，0.20g和0.40g时，近断层脉冲型和非脉冲型地震作用下的隔震层最大位移如图3所示，可以看出，随着脉冲周期的增长，隔震层位移有一定的增长趋势，但无较强的相关性.表4给出了近断层地震作用下隔震层位移的最大值和平均值.由图3和表4可知：① 当PGA相同时，近断层脉冲型地震动作用下的隔震层响应大于近断层非脉冲型地震动；② 近断层脉冲型地震动作用下，不同PGA的隔震层位移曲线形态相似，仅数值变化，且每条地震波的变化比例均接近于PGA比值，如PGA＝0.40g和PGA＝0.20g隔震层位移的比值介于1.95—2.05 （PGA比值的±2.5%）之间；③ 近断层脉冲型地震动作用下，PGA＝0.20g与PGA＝0.07g，PGA＝0.40g与PGA＝0.20g隔震层位移平均值比值分别为2.86和2.01，与PGA的比值基本相同.

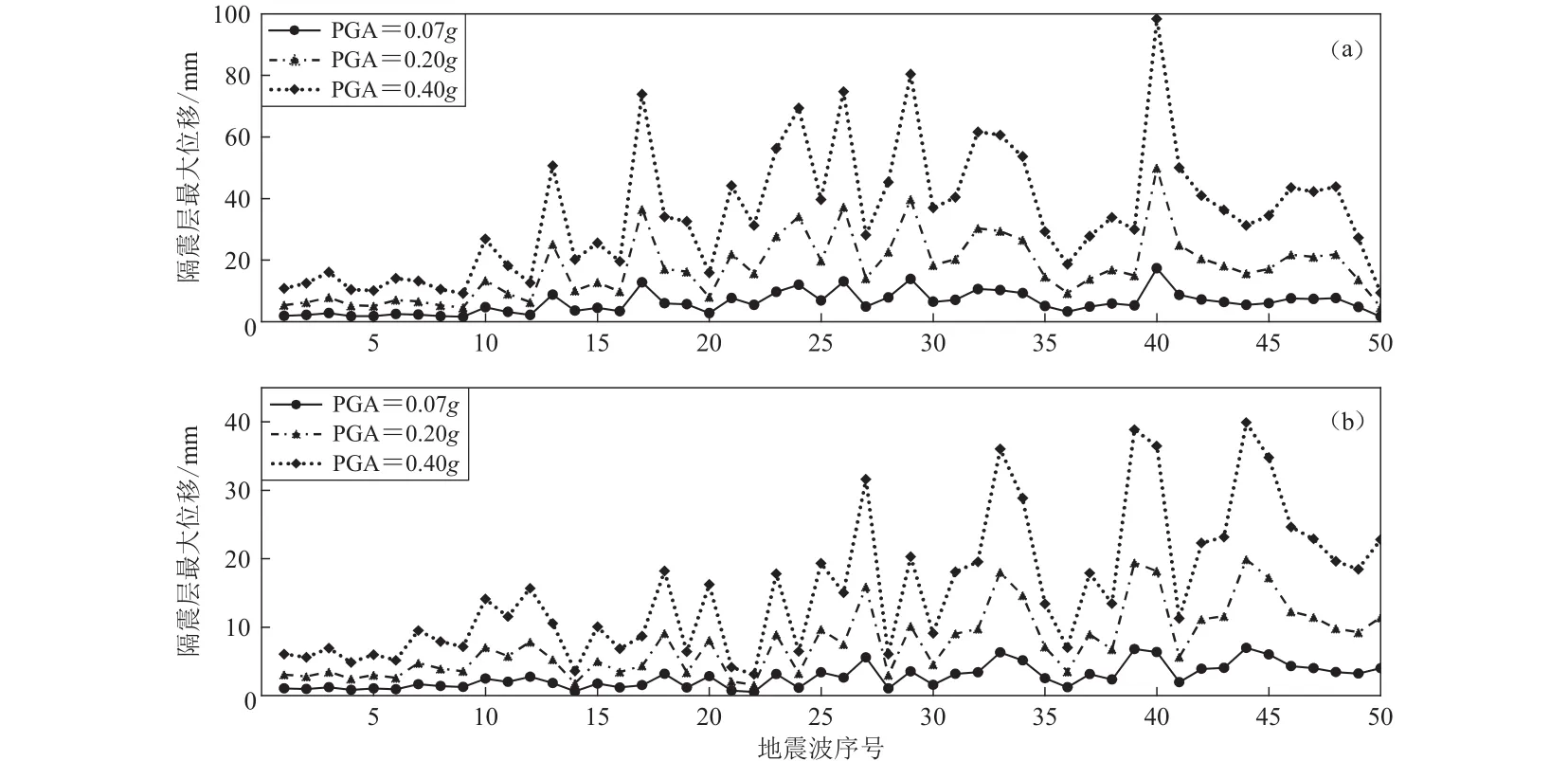
图3 不同PGA时近断层地震作用下的隔震层最大位移对比（a）近断层脉冲型地震动作用；（b）近断层非脉冲型地震动作用Fig.3 Comparison of maximum displacement of isolation layer under near-fault ground motions with different PGAs（a） Near-fault pulse-like ground motions；（b） Near-fault non-pulse-like ground motions

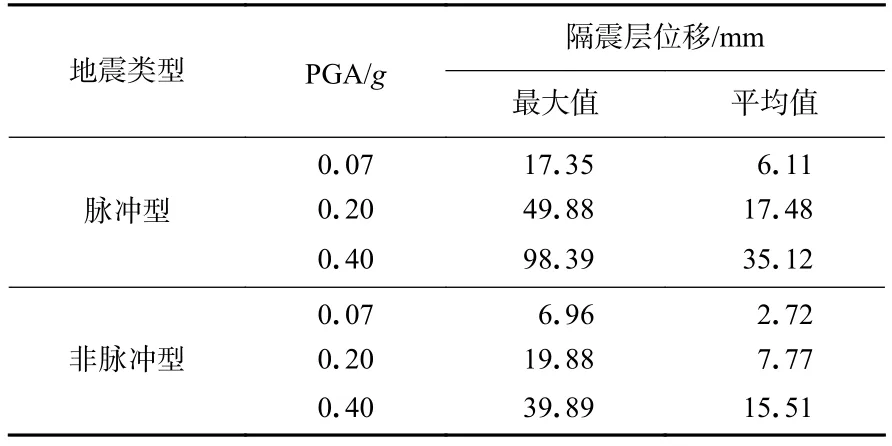
表4 隔震层位移对比Table 4 Comparison of displacement of isolation layer

图4给出PGA分别为0.07g，0.20g和0.40g时，耦合隔震结构体系的楼层层间位移的平均值曲线.由图4可知，近断层脉冲型地震作用下，不同PGA的层间平均位移曲线的形态相似，仅数值变化，变化比例与PGA的比值接近，故本文后续仅挑选PGA＝0.07g的工况分析结构响应与脉冲特性的相关性.

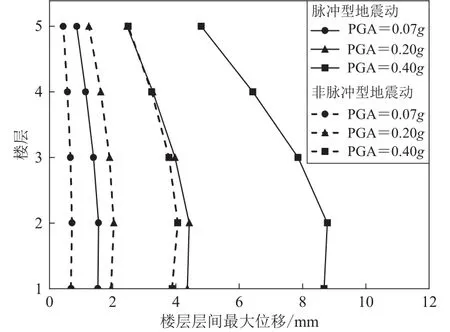
图4 不同 PGA 时近断层地震作用下的层间最大位移Fig.4 Maximum interlayer displacements under nearfault ground motions with different PGAs

3.2 设备响应

在PGA为0.07g，0.20g和0.40g时，50条近断层脉冲型地震动作用下的设备位移和顶层加速度的最大值如图5和图6所示.因地震波的非平稳特性，每条地震波在各个频带的能量存在显著差异，即使在结构基本频率附近频带内能量相近的两条地震波，也会因为在时域中瞬时能量的差异导致结构响应的巨大差别，因此当各地震波经隔震层传递至上部结构时，虽然其顶层加速度的主频均与耦合体系的基本频率接近，但顶层加速度的最大值仍存在较大差别，从而导致设备位移的最大值随地震波变化.

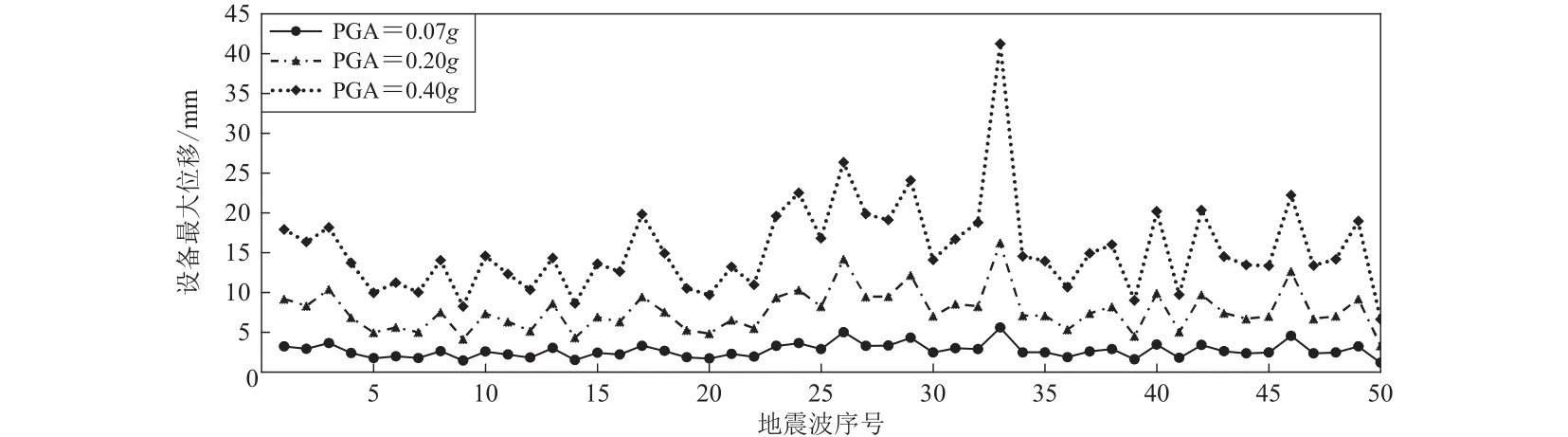
图5 不同PGA的近断层脉冲型地震动作用下设备最大位移对比Fig.5 Comparison of maximum equipment displacement under near-fault pulse-like ground motions with different PGAs

图6 不同PGA的近断层脉冲型地震动作用下顶层最大加速度对比Fig.6 Comparison of maximum acceleration of top floor under near-fault pulse-like ground motions with different PGAs

由图5可见，近断层脉冲型地震动作用下，不同PGA的设备位移曲线形态整体相似，仅数值变化，且大部分地震波的变化比例与PGA的比值接近；当PGA＝0.20g和PGA＝0.07g时，设备位移的比值介于2.78—2.92 （PGA比值的±2.5%）之间；当PGA＝0.40g和PGA＝0.20g时，设备位移的比值介于1.95—2.05 （PGA比值的±2.5%）之间（共35条）.通过分析模型的局部应力可知，当PGA＝0.40g时，设备在运动过程中进入塑性的程度大于PGA＝0.20g时，且因设备尺寸较小，对设备整体变形影响较大，从而导致某些地震波在PGA＝0.40g和PGA＝0.20g时，设备位移的比值与PGA的比值有较大不同.

通过对比图3a与图5发现，引起隔震层和设备最大变形的地震波不同，分别为40号和33号地震波.设备响应主要与顶层楼面响应时程有关，与地震波的关系需考虑主体结构的影响.对比图3a与图6可知，引起较大隔震层位移的地震波，同时伴随着较大的顶层楼面加速度.综上可得，近断层脉冲型地震动引起隔震层较大变形的同时，引起顶层楼面加速度较大的概率极大，但对设备的影响，需结合楼面加速度时程的频谱特性以及结构与设备之间的耦合关系确定.

4 脉冲影响分析

因分析过程中需对每条地震波时程进行脉冲提取，故采用较易操作的零交法（Rodriguez-Marek，2000；徐龙军，谢礼立，2005）确定时程中的脉冲数量及相应的周期.以速度时程为主要分析对象，同时结合加速度脉冲进行辅助分析；取脉冲峰值速度大于峰值速度（peak ground velocity，缩写为PGV）的30%作为速度脉冲的确定准则（刘启方，2005）.为方便对比，对地震波的加速度和速度时程进行了归一化处理.

4.1 隔震层位移与速度脉冲的对应关系

图7给出了三种地震波速度脉冲与隔震层最大位移的关系：① 最大位移处不存在速度脉冲（图7a），包括1，3，4，7，11，17，22，23，24，32，33，43和45号共 13条地震波（占比26%）；② 最大位移处存在速度脉冲，但不是最大速度脉冲（图7b），包括2，5，15，16，18，19，21，26，27，28，29，30，31，34，35，37，38，39和41号共19条地震波（占比38%）；③ 最大位移处对应最大速度脉冲（图7c），包括 6，8，9，10，12，13，14，20，25，36，40，42，44，46，47，48，49和50号共18条地震波（占比36%）.

图8为上述类型①中32号地震波作用下结构最大位移与地震波加速度脉冲关系图可见，相比于地震波速度时程，加速度时程的相位明显提前于隔震层位移时程.通过图7a与图8的对比可知，32号地震波作用下，隔震层最大位移处没有速度脉冲，但存在加速度脉冲.

图7 隔震层最大位移与速度脉冲的三种对应关系（a）最大位移处无速度脉冲（32号地震波）；（b）最大位移处不对应最大速度脉冲（28号地震波）；（c）最大位移处对应最大速度脉冲（10号地震波）Fig.7 Three correspondences between the maximum displacement of isolation layer and the velocity pulse（a） No velocity pulse corresponds to the maximum displacement （seismic wave No.32）；（b） Maximum velocity pulse does not correspond to the maximum displacement （seismic wave No.28）；（c） Maximum velocity pulse corresponds to the maximum displacement （seismic wave No.10）

图8 最大位移与加速度脉冲的关系（32 号地震波）Fig.8 Maximum displacement of isolation layer versus acceleration pulse （seismic wave No.32）

综上可得，基于速度脉冲可分析大部分脉冲地震动作用下的结构响应，若最大响应处没有速度脉冲，可尝试结合加速度脉冲进行分析.

4.2 隔震层最大位移与对应脉冲的相关性分析

由图3a可知，40号地震波引起的隔震层位移最大，29号地震波次之.为分析引起隔震层较大位移的原因，采用

计算速度脉冲对应的能量，式中，t1和t2分别为脉冲的开始和结束时刻，a（t）为脉冲段对应的加速度.

计算结果显示，40号地震波的速度脉冲对应的能量E最大；29号地震波的速度脉冲对应的能量E虽不是最大，但脉冲周期为0.86 s，与结构基本周期最近.后文将基于脉冲周期与结构基本周期的相近程度以及脉冲能量E进行分析.

4.2.1 隔震层最大位移处存在速度脉冲

对37条隔震层最大位移处存在速度脉冲的地震波（即上节类型②和③）进行相应的脉冲周期TP识别，同时对速度脉冲对应的能量E进行计算.

隔震层最大位移与周期比TP/T（37条地震波隔震层最大位移处的脉冲周期TP与结构基本周期T的比值）的关系，如图9a所示.一般认为当TP/T＝1时，容易引起结构的较大响应，故以TP/T＝1为界线计算相关系数；当TP/T＜1时，两者相关系数为0.80；当TP/T＞1时，两者相关系数为-0.07.隔震层最大位移与脉冲能量E的关系，如图9b所示，可见：隔震层响应随着脉冲能量E的增大，整体呈增大趋势，而根据周期比进行分界并计算相关系数结果显示：当TP/T＜1时，隔震层最大位移与脉冲能量E的相关系数为0.46；当TP/T＞1时，两者相关系数为0.79.

图9 隔震层位最大移与周期比 TP/T （a）和脉冲能量 E （b）的关系Fig.9 Displacement of isolation layer versus period ratio TP/T （a） and pulse energy E （b）

通过计算发现，当TP/T＞1时，所选地震波的脉冲平均能量为TP/T＜1时的1.90倍，即当脉冲周期较小时，相应脉冲能量E普遍偏小；当脉冲周期较大时，相应脉冲能量E普遍偏大.

综上可得：当周期比TP/T＜1时，周期比对结构响应的影响大于脉冲能量E；隔震层响应随着脉冲周期与结构周期的接近，整体呈增大趋势.当TP/T＞1时，周期比的影响小于脉冲能量E，即会出现当脉冲周期远大于结构周期，但因脉冲能量E大，导致结构响应大的现象（如40号波），此亦可作为当TP/T＞1时隔震层最大位移与周期比TP/T的相关系数仅为-0.07的解释.

4.2.2 隔震层最大位移与对应脉冲的拟合关系

虽然地震波的速度时程相比于加速度时程高频分量较少，但部分地震波的速度脉冲过程中仍会存在明显波动.通过对比发现，该部分波动主要缘于速度脉冲区域对应加速度曲线的穿零次数；加速度曲线的穿零次数越多，对速度脉冲的影响越大，从而影响结构的响应.穿零次数，即为速度脉冲区域对应加速度曲线穿过时间轴的次数（谭潜等，2019）.由图10的穿零次数与速度脉冲波动关系可见：当穿零次数较少时，速度脉冲（图中黑框区域的脉冲）整体平滑，如图10a所示；当穿零次数较多时，速度脉冲存在多次波动，如图10b所示.

图10 穿零次数为 1 （a）和 9 （b）时速度脉冲对应的加速度曲线Fig.10 Acceleration curves corresponding to velocity pulse with zero-crossing times 1 （a） and 9 （b）

为排除速度脉冲区域波动的影响，同时考虑适用性，对速度脉冲对应加速度曲线穿零次数≤5的21条地震波进行拟合分析.因隔震层最大位移随着脉冲周期与结构周期的接近以及脉冲能量E的增大，整体呈增大趋势，故选取二元二次函数进行拟合；自变量为周期比TP/T（x1）和脉冲能量E（x2），因变量为隔震层位移比y（隔震移层最大位移与隔震支座橡胶层总厚度之比），其拟合关系为

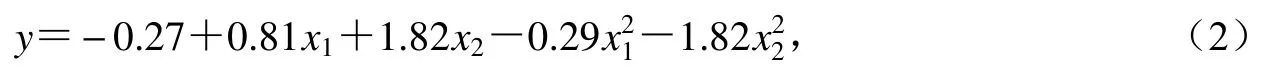
判定系数r2＝0.94.

4.3 设备位移与地震波脉冲特性的关系

由图3a，图5和图6可知，若近断层脉冲型地震动引起的隔震层位移最大，同时引起最大顶层楼面加速度的概率极大，但设备位移的大小需结合楼面加速度时程具体分析.通过对顶层楼面加速度时程的频谱分析可知，近断层脉冲型地震波传至顶层楼面时，其主频已与耦合隔震体系的基本频率近似，而设备频率与该频率相距较远，故顶层楼面加速度峰值最大并不代表肯定能引起最大的设备位移.设备相对于顶层楼面属于单质点体系，设备最大位移与顶层楼面加速度时程的反应谱值（设备周期0.25 s）的关系如图11所示，两者相关系数为0.99.据此可知，设备响应与顶层楼面加速度直接相关.

图11 设备周期为 0.25 s 时设备位移与顶层楼面加速度时程的位移谱的关系Fig.11 Relationship between equipment displacement and displacement spectrum of top floor acceleration time histories when the period of the equipment is 0.25 s

图12给出了高频分量较丰富的23号波的加速度和速度时程以及结构顶层的楼面加速度和速度时程.由图可知：楼面加速度和速度时程整体平缓，存在多个脉冲（图12a），与地震波的加速度和速度时程（图12b）的高频波动存在显著差别.