我国大陆地区常用浅壳地震的地震动参数衰减关系＊

肖 亮 俞言祥

（中国北京 100081 中国地震局地球物理研究所）

引言

地震动参数衰减关系，近年也常被称为地震动预测方程，即采用模型化的方式来进行地震动参数预测，是地震动参数区划、重大工程场地地震安全性评价等工程实践中的关键一环（胡聿贤，1999）.其基本理念是基于实际的地震观测资料或者地震动模拟结果，采用经验性或者基于理论的衰减模型，通过统计回归确定模型系数.在应用时，通过给定的震级、距离、场地条件参数等，直接计算相应场点的地震动参数均值，并可以通过离散模型给出相应的地震动概率分布.

我国大规模强震动观测起步稍晚，但是由于具有非常丰富的历史地震烈度资料，在地震烈度衰减关系方面的研究成果也颇为丰富，我国前三代地震烈度区划图即以此为基础.近数十年，工程抗震设防转向使用峰值和反应谱等地震动参数为依据，我国大陆地区的地震动参数衰减关系研究得以发展，取得了诸多研究成果.

从全国性的衰减关系研究上来看：霍俊荣（1989）使用当时较新的美国西部地区强震资料（较多为模拟式记录）确定了美国西部的水平向、竖直向峰值和反应谱的衰减关系，并基于中美两国烈度衰减关系的差异采用转换修正的方式建立了我国四个地震动分区的衰减关系；俞言祥和汪素云（2006）使用美国西部强震资料（主要是数字记录）和宽频带速度记录重新回归了美国西部地区的水平向长周期衰减关系，并采用四代图编制过程中形成的烈度衰减关系，通过上述两种衰减关系的转换修正建立了我国东、西部两个地震动分区的反应谱衰减关系；肖亮（2011）以及肖亮和俞言祥（2021）使用美国下一代地震动衰减模型（next generation attenuation model，缩写为NGA）强震数据库的资料以及新近补充的宽频带速度记录，在俞言祥和汪素云（2006）的基础上，采用分段线性模型重新回归了美国西部地区的水平向长周期衰减关系，进而采用五代图编制过程中建立的我国分区烈度衰减关系，经转换修正得到了我国四个地震动分区的反应谱衰减关系.这几组衰减关系面向的地震动分区较大，基本覆盖了我国大陆地区浅壳地震的地震动参数估计需求，因此被广泛用于实际工程抗震设防.

地震动参数衰减具有地区性差异，也有很多研究人员利用当地的记录在更小尺度上进行更精细化的研究.特别是2008年汶川地震之后，我国在西南地区布设的强震台网获取了一批高质量强震记录，很多研究据此展开.雷建成等（2007）收集了西南地区和四川盆地百余次破坏性地震的资料，重新校核了各地震的震级参数，确定了该地区的地震烈度衰减关系，并在此基础上通过转换修正重新回归了四川及邻区的基岩水平向反应谱衰减关系；卢大伟等（2010）利用汶川地震强余震流动观测获取的强震记录，分析了汶川中强余震的峰值和反应谱的衰减特性，并回归了衰减关系；喻烟（2012）收集了汶川地区周边的强震记录，对汶川邻区的峰值和反应谱衰减关系进行了研究；王玉石等（2013）基于川滇地区强震资料回归了川滇地区水平向峰值和反应谱的衰减关系；张斌等（2021）收集了西南地区79次MS4.0—8.0强震资料，通过统计回归得到了西南地区包含震级饱和效应、几何衰减、线性与非线性场地响应、非弹性衰减的水平向峰值速度、峰值位移的衰减关系；胡进军等（2021）基于四川西昌附近21次地震的千余条地震记录，分析了区域性衰减模型中震级项、距离项和场地项的特征，建立了符合西昌地区地震动特征的衰减关系.从上述研究成果可以看出，其大多聚焦于中等或小尺度地区，而全国范围工程抗震设防应用上常使用更大区域的衰减关系模型.

本文拟在上述研究的基础上，简要介绍地震动参数衰减关系应用时涉及的地震动参数、地震参数、基本模型、回归方法等方面的要点，并以华北地区为例，对数十年以来我国工程应用中常用的几组有代表性的衰减关系的主要特点进行阐述.这几组衰减关系涉及的区域尺度更大，完整覆盖我国陆域基岩场地，较好地反映了大震近场饱和效应等工程应用关注的地震动特性，能够满足我国抗震设防应用的需求.本文涉及的范围主要是我国大陆地区浅壳地震的衰减关系，未包含深源、俯冲带地震的内容.

1 地震动参数

地震动的复杂特性决定了地震动研究须考虑多方面的因素，其中最为直观简便的研究方法就是研究代表地震动相关特性的地震动参数.在过去数十年的研究中，研究者对于地震动参数的定义非常多，包括各种幅值类参数、持续时间类参数、能量参数等.在工程抗震设防应用上，较常用的参数主要有地震动峰值、反应谱值及强度包络函数等.

1.1 地震动峰值

地震动峰值通常定义为场点地震动时程峰值的最大值.从最早采用强震观测仪器获取强震动资料以来，研究最为广泛的地震动参数之一就是地震动峰值，如峰值加速度（peak ground acceleration，缩写为 PGA）、峰值速度（peak ground velocity，缩写为 PGV）和峰值位移（peak ground displacement，缩写为 PGD）等.对于大多数低矮的建筑物（自振周期小于 0.3 s），可以只关注PGA的影响；对于输油输气管道、长跨桥梁、超高层建筑等对速度、位移敏感的建筑物的抗震设计，需要专门考虑 PGV或PGD的影响.

1.2 地震动反应谱

单一的地震动峰值显然无法对地震动时程的频域特性进行全面的表述.随着强震记录和震害资料的逐渐积累，研究人员逐渐认识到地震动峰值与建筑物的地震反应之间并不是简单的一一对应关系.不同自振周期的建筑受不同周期地震动成分的影响，也即地震动反应谱的原理.地震动反应谱概念的提出，使得地震动研究进入动力反应分析阶段.

若将建筑简化为单自由度振子体系，其反应谱定义为一个自振周期为T、阻尼比为ζ的单自由度振子，在地震动a作用下，振子反应时程y的最大振幅y（T，ζ）为随自振周期T变化的函数.当y为单自由度体系的相对位移、相对速度或绝对加速度时，y（T，ζ）可分别称为相对位移、相对速度或绝对加速度的反应谱.目前大多数重要工程抗震设计已将地震动反应谱考虑在内.

1.3 持时与强度包络函数

除幅值参数以外，强地震动的持时也是地震动特性的重要参数之一.地震动时程常被分为三段，即由弱至强的上升段、强震动平稳段和由强至弱的衰减段.引入强度包络函数对其进行描述，我国工程中广泛采用的一种函数形式（胡聿贤，1999）为

该模型使用t1和t2作为平稳持续段的端点时刻，采用指数下降的函数形式描述下降段，c为下降段的衰减系数.该模型形式简单，可较好地描述强度包络函数的变化规律，常用于我国现行的重大工程场地地震安全性评价的人工地震动合成中.

1.4 水平向分量的考虑

目前大部分研究主要是针对水平向地震动参数，而对于两个水平向分量，根据研究目的可以有多种选取方式.有研究为了丰富统计样本量，同时更好地考虑离散不确定性，将两个分量当做独立记录进行统计分析（霍俊荣，1989；俞言祥，汪素云，2006；肖亮，2011；肖亮，俞言祥，2021）；有研究为了减小离散性，使用两个分量的几何平均值或算术平均值作为研究对象（卢大伟等，2010）；近年美国NGA衰减关系采用两个分量旋转合成地震动时程矢量，选取50分位数等结果作为水平向取值，这主要是考虑两个水平分量受方位角变动的影响（Abrahamsonet al，2014）.因此，在使用相关研究结果时，应关注不同研究所给出定义之间的差异.

1.5 其它地震动参数

除了以上常见的地震动参数外，近年还有其它的地震动参数逐渐被关注，如表征地震动能量的阿里亚斯强度、表征斜坡刚体位移的纽马克位移等（李伟等，2017；李雪婧等，2021），这些参数与地震滑坡密切相关，在地震滑坡风险防治、滑坡成灾机理研究方面具有较强的应用价值.

2 衰减关系模型

地震动参数衰减关系常使用基于理论或者经验的方程式作为先验模型，将地震参数作为自变量、地震动参数作为应变量，基于强震记录进行统计回归，从而确定方程式的各项系数，以实现对目标场点地震动参数均值及其离散性的预测.

2.1 地震参数研究

地震参数指的是衰减关系模型中的自变量输入.从理论上讲，场点的地震动受到震源特性、传播路径、局部场地条件等因素的影响.因此，选择地震参数一般均需考虑震源释放能力、震源与场点的距离和场点的场地特性.常用的地震参数主要有震级、距离和场地参数.

2.1.1 震级参数

震级是衡量震源释放能量大小的指标之一.不同的震级标定方法使得震级的数值有较大差异，由此对衰减关系模型也产生相应的影响.衰减关系常用的震级标定主要有地方震级ML，面波震级MS和矩震级MW等.

地方震级ML是由短周期波形振幅进行标定，在强震记录尚不丰富的时期，常用小震近场记录进行震级标定，因此早期的许多研究常采用ML进行衰减关系研究.其不利之处在于ML随震源尺度的增长会很快出现饱和，且容易受制于地方台站区域性的限制.

面波震级MS采用更长周期的面波进行标定，较不容易出现饱和现象；由于该震级标定使用的是远场面波，因此在全球范围内基本遵从同一标定原则，具有统一性.鉴于该特性，较多研究选用面波震级MS开展衰减关系研究（霍俊荣，1989；俞言祥，汪素云，2006），我国工程应用中也常选用面波震级.

近些年研究显示随着震源尺度的不断增长，面波震级MS也会出现饱和现象.而矩震级MW与地震震源尺度和断层滑动量相关，不会随着震级增大而饱和，适用于大震衰减关系的研究，因此有研究选用矩震级MW作为震级描述（胡进军等，2021）.矩震级的不利之处在于其计算需要有限断层模型，很多历史地震和中小地震往往缺乏统一的矩震级结果.

2.1.2 距离参数

距离针对的是从震源到场点的传播路径对地震动影响的简化描述.不同研究对于距离的定义不尽相同，常用的距离参数主要分为两类：一类是点源模型的距离参数，如震中距（场点至地震震中的距离）、震源距（场点至地震震源的距离），其定义在断层破裂尺度较小时是合理的，具有计算简单、直观的特点；另一类是断层模型的距离参数，如断层投影距（场点至断层地表投影面的最短距离）、断层距（场点至有限断层面的最短距离），其特点是考虑了断层破裂尺度的影响，更加适合于近断层、精细化研究，缺点是需要可靠的有限断层模型，计算相对复杂.以上两类定义的差异主要表现在近场区域，在远场范围差异很小.

2.1.3 场地条件参数

场地条件用于描述局部场地因素对近地表地震动的影响，一般倾向于以分类的方式进行衰减关系统计，对每一个场地分类给出合适的地震动参数估计.在没有足够的场地分类描述依据时，通常采用宏观地质描述的方式将场地粗略地划分为土层（硬土，软土）、基岩（硬基岩，软基岩）等；当台站钻孔资料丰富时，也可采用土层剪切波速作为分类标准，这种方式采用明确的钻孔资料作为依据，相较于地质描述方式更加合理，物理意义明确.

近些年随着台站信息的逐步丰富，也有研究直接采用浅地表剪切波速作为自变量的方式参与模型建立（胡进军等，2021），详见下文.

2.2 衰减模型

衰减模型是基于理论或者经验的数学模型，反映了研究者对于地震波能量随地震参数变化规律的认识.在地震资料不足以完全覆盖的部分，衰减模型通过引入先验信息提供外推约束.一般而言，衰减模型包括震源、传播路径和场地条件等模型，表示如下：

式中，f（M）为震源模型，f（R）为传播路径模型，f（site）为场地条件模型，ε为均值为 0 且具有标准差σ的随机项.下面对各项分别进行简述.

2.2.1 震源模型

震源模型描述了地震动参数随震级的变化规律.早期研究常用震级的线性项来描述地震动参数随震级的增长，如式（3）所示.在这种情况下，假定只要震级增大，地震动参数即线性增大.

式中，M为震级，a和b为回归系数.

然而对于常用的峰值或者高频的反应谱值而言，这些参数并非随震级的增大而无限增大，而是存在一个饱和上限，即所谓的震级饱和效应.因此，为了反映震级饱和效应，许多研究在线性模型的基础上进行了相应的改进.常用的改进方式之一是引入二次项的形式来描述，如式（4）所示.在该模型中，随着震级的增大，地震动参数的增长率逐渐减小.

式中，M为震级，a，b和c为回归系数，c通常为负值.

另一种考虑震级饱和效应的方式，是对不同震级进行分段，如式（5）所示.

式中，M为震级，a1，a2，b1和b2为回归系数，Mc为截止震级.

在该模型中，不同震级段内，地震动参数随震级的增长率不同.当然也有很多变体，如分段更多，在各分段内采用二次函数形式等.

除了震级以外，随着强震资料的逐渐丰富，研究者们发现不同的震源机制对地震动也会产生不同的影响.一种常见的模型形式是对于不同的震源机制，在震级模型的基础上对不同断层类型赋予不同的常数，如式（6）所示.有时由于正断层类型的样本偏少，也常将正断层与走滑断层类型进行合并.

式中：f（base）为基础模型；fNor，fRev和fStr分别表示正、逆和走滑断层的类别，当断层类型为对应类别时该项为1，否则为0；d1，d2和d3为回归系数.

2.2.2 传播路径模型

地震动时程是不同种类地震波的叠加组合，各成分随距离的衰减率不尽相同.在不同距离上控制地震动参数的地震波可能属于不同的类型，这就造成了地震动参数距离衰减率的复杂性.作为面向实际工程应用的模型，需要对复杂的距离衰减模型进行一定的简化处理.比较常用的距离衰减模型主要是以下面几种为基础.早期研究限于强震资料数量，对于大震近场距离饱和效应的研究不多，常采用常数项的尺度因子，如式（7）和式（8）所示.该模型避免了距离为0处取对数的问题，适用于中小震级.

式中，R为距离参数，h0为尺度因子，c和h0为回归系数.

随着对地震动特性认识水平的逐步提高，研究者认识到高频地震动在近场区域的衰减要显著缓于中远场，即大震近场距离饱和效应.一种常用的方式是将尺度因子变化为随震级M指数增长的饱和因子，如式（9）所示.

式中，R为距离参数，M为震级，c，d和e为回归系数.

由式（8）可知，大震级时衰减缓慢的近区域范围要显著大于中小震级.还有一种方式是将距离的指数衰减项写为震级的线性函数，如式（10）所示，其中随震级M变化的项作用于对数项外面.这样的情况下，不同震级的衰减曲线不再平行，而是具有喇叭口一样的形状，越大震级的曲线衰减越缓慢.

式中，R为距离参数，M为震级，c，d和h0为回归系数.

对于远场地震动来说，有时需要考虑地震动的非弹性衰减，常用与距离成正比的项kR来对其进行描述，其中参数k为回归系数，其值非常小，在工程应用的近场区域为简单起见此项常被略去.

2.2.3 场地条件模型

放电操作模式下,输入端为5节18650电池组,输出端负载电阻为30 Ω,保持输出端电压U1=30±0.5 V。记录输入电流I2和输入电压U2。则放电效率为:如表2所示。

场地条件模型描述了地震动参数随局部场地条件的变化规律.一般来说，对于同等震级-距离处的自由地表的基岩场地与土层场地，二者的地震动参数具有一定的差异，不应将其混用.

为了反映场地的影响因素，一种简单的处理手段是进行衰减关系回归时，仅采用目标场地条件的记录，而舍弃其它场地条件的记录.此种方法假定不同场地分类中地震动参数随震级、距离的变化关系是不同的，其局限在于每类场地条件中必须要有足够数量的资料.

另一种处理手段是采用因子的形式使不同场地条件之间的地震动参数产生联系，如式（11）所示.该模型以基岩地震动作为参考，认为不同场地的结果相比基岩应乘以一定的调整系数.

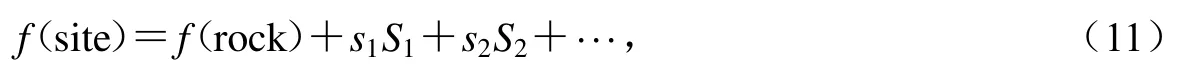
式中：f（rock）为基岩场地的模型；S1和S2分别表示各类场地类别，当场地为对应类别时该项为1，否则为0；s1，s2， ···为回归系数.

该方法的优势在于可以利用土层和基岩的数据进行模型构建，扩展了资料集；其局限在于需要事先确定不同场地分类的地震动参数之间的相互关系，而且使用常数因子的情况下，即土层与基岩的地震动衰减曲线平行，这一假定与土体的非弹性效应不相符.

为了解决土层与基岩场地的地震动衰减曲线平行的问题，一些研究向土层效应因子中添加震级、距离与幅值相关项，使用vS30（地表30 m内等效剪切波速）作为自变量，美国NGA衰减关系多使用此种模型.作为其中一个例子， NGA-west2数据库中ASK14 （Abrahamsonet al，2014）所采用的场地模型形式如下：

上面的模型使得不同vS30的放大效应与参考基岩面的反应谱幅值相关，在vS30超过vlin之后体现为线性土体放大，在更软弱场地体现为土体非线性效应，总体来看相对复杂.

我国现阶段工程应用大多采用基岩的衰减关系进行地震动参数估计，再使用钻孔资料进行土层动力反应分析，或者使用不同场地的地震动参数换算表来估计其它场地的地震动参数.一般不直接使用土层的衰减关系.

3 衰减关系的回归方法

最小二乘法是目前进行衰减关系回归的最常用方法之一，然而由于不同衰减关系的模型越来越复杂，模型参数之间也存在相关性，简单的最小二乘法已经无法满足需求，需要考虑更为复杂的回归策略.

由于更大的地震总是被更远的台站所记录到，大部分强震资料中普遍存在震级与距离之间的相关性，但是这种相关性会造成使用简单最小二乘法时，震级项与距离衰减项的回归系数之间存在耦合，类似于“跷跷板”效果，即改变其中任一系数均会造成另一个系数的相应改变.Joyner和Boore （1981）提出经典的两步回归方法，在第一步引入虚拟变量对距离衰减项进行回归，如式（14）所示.第一步通过回归确定每一个地震事件的震级项ai以及下式中的参数b和c.

式中：Y为地震动参数；R为距离；S为场地类别；Ei为对应第i个地震事件的虚拟变量，对于第i个地震事件取1，否则取0；ai，b和c为回归系数.

第二步对震级项系数进行回归，如式（15）所示：

式中：Mi表示第i个地震事件的震级；α，β和γ为回归系数.对于所有地震，回归震级项与震级的函数关系.

两步法利用虚拟变量解决了震级-距离耦合的问题，得到了更为合理的回归参数.后期很多研究都在该方法的基础上，针对各自的研究模型进行改进.

除震级-距离耦合的问题以外，实际的记录还表现出震级-距离平面上的不均匀分布，特别是大震近场、小震远场资料的稀缺，而在中等震级-距离处有非常多的数据.这种效应的影响常使用加权等方式来消除，如霍俊荣（1989）采用震级、距离加权的方法，对每个震级距离统计单元赋相同的权重.该方法可在一定程度上减低某些丰富记录的地震事件对整体结果的影响.

随着衰减模型的复杂化，大量非线性模型被引入，模型参数之间的相关性已不容忽视，任一参数的微小变动都可能对其它参数产生很大的影响，连各参数回归时的先后顺序也会影响最终的结果，所以目前较新的衰减模型一般都需要制定回归策略.也有很多新方法如最大似然法、随机效应法被引入，并通过多次不同子数据集的回归来确保最终得到稳定的回归结果.篇幅所限在此无法详述，详细情况可参考相应的文献（Brillinger，Preisler，1984，1985；Abrahamson，Youngs，1992；Joyner，Boore，1993）.

4 我国工程常用衰减关系

随着强震资料的不断积累和社会经济水平的逐渐提高，我国不同阶段的工程实践对地震动参数估计提出了更多新要求.与之相对应的，我国工程实际常采用的衰减关系是不断发展前行的，地震动参数从最早的地震烈度逐步发展到峰值加速度、反应谱等.

现阶段的抗震设防主要采用峰值加速度和反应谱作为参考依据，下面将以华北地区为例，对我国工程实际常用的几套水平向基岩峰值加速度与反应谱的衰减关系进行简述.需要说明的是，许多研究人员对衰减关系开展了很多卓有成效的研究，但此处限于篇幅，无法对所有研究进行阐述.

4.1 霍俊荣模型

霍俊荣（1989）在其博士论文中提出了考虑关系式中所有随机变量不确定性综合影响的一致加权最小二乘回归法，基于此方法利用当时最新的强震资料（其中很大一部分是模拟强震记录），建立了美国西部地区峰值加速度、速度、位移和反应谱的衰减关系，并详细讨论了模型化之后各地震动参数随震级、距离的变化规律.此外，还利用烈度资料换算地震动参数的方法，建立了我国四个大区的地震动峰值和反应谱的衰减模型，其中华北区水平向峰值加速度Ⅱ型模型的表达式为

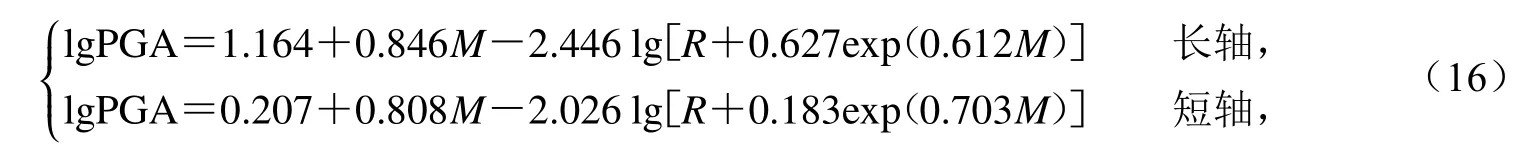
式中M为面波震级，R为震中距，标准差为0.260.该模型主要特征是震级项采用线性函数形式，距离衰减项采用含有指数形式的近场饱和因子，二者共同作用来反映大震近场距离饱和现象.受篇幅限制，其余如反应谱的系数等请参考霍俊荣（1989）.

4.2 四代图模型

在我国第四代地震动参数区划图（国家质量技术监督局，2001，以下简称四代图）的编制过程中，俞言祥和汪素云（2006）使用单变量回归方法，利用当时美国西部的最新强震资料，使用单变量回归方法重新回归了参考区的水平向短周期反应谱衰减关系，并利用美国南加州数字宽频带记录建立了参考区的水平向长周期反应谱衰减关系，在2 s周期附近接合得到了参考区的水平向反应谱衰减关系；之后通过四代图编制时搜集新烈度资料重新拟合得到的我国东、西部地区的分区烈度衰减关系，采用烈度转换修正的方法，建立了我国东部和西部地区的基岩水平向峰值加速度和反应谱的衰减关系.式（17）给出了中国东部地区水平向峰值加速度衰减关系的数学表达式：

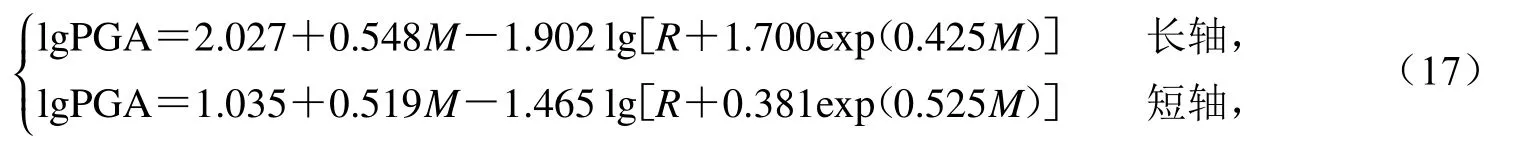
式中M为面波震级，R为震中距，标准差为0.240.其主要特征是震级项采用线性函数形式，距离衰减项采用含有指数形式的近场饱和因子，二者共同作用能够较好地反映大震近场距离饱和现象.反应谱的系数请参考俞言祥和汪素云（2006）.

4.3 五代图模型 （ 基于强震的2011模型、长周期修正的区评2019模型 ）

在我国第五代地震动参数区划图（中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会，2015，以下简称五代图）的编制过程中，吸收了国际上对地震动新的认识及衰减关系建立过程中的新技术方法，使用美国NGA强震数据库提供的高质量数字强震记录，在考虑继承性和易用性的基础上，肖亮（2011）使用分步回归法建立了一套基于强震的美国西部基岩水平向地震动参数衰减关系，之后利用五代图编图新近补充的烈度资料重新回归了基于五代图新分区的地震烈度衰减关系，通过转换修正得到了与五代图相配套的我国分区水平向峰值和反应谱的衰减关系（周期至6 s）.

为了响应我国长周期建筑抗震设防的迫切需求，肖亮和俞言祥（2021）利用新近补充的美国西部地区宽频带速度基岩记录，对肖亮（2011）结果的长周期（周期＞1.2 s）部分进行修正，通过烈度转换得到了我国分区水平向长周期反应谱的衰减关系（周期至10 s）.该套衰减关系已在“区域性地震安全性评价工作大纲（试行）”（中国地震局，2019）中作为推荐性附录在地震系统印发，简称为区评2019模型.

上述两模型对于峰值加速度和反应谱在周期1.2 s之前是一致的，式（18）和（19）分别给出了华北区水平向峰值加速度衰减关系长轴和短轴方向的数学表达：

长轴：

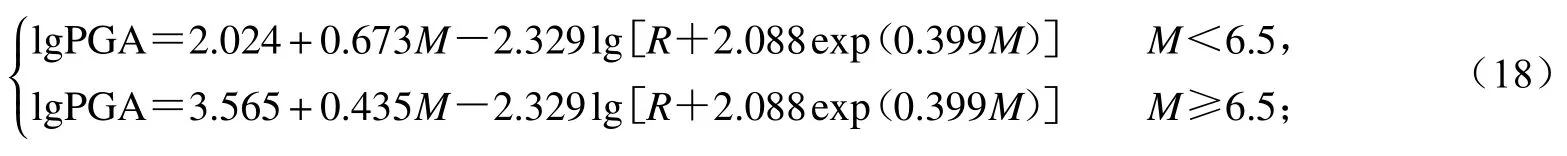
短轴：

式中M为面波震级，R为震中距，标准差为0.245.其主要特征是震级项采用分段线性函数形式，距离衰减项沿用了四代图含有指数形式的近场饱和因子，二者共同作用能够较好地反映大震近场的震级、距离饱和现象.反应谱的系数请参考肖亮和俞言祥（2021）.

图1给出了上述三种模型的峰值加速度在长轴、短轴方向随震中距的变化，可以看出：在中等震级（M＝6—7）、中等距离（R＝10—100 km）处，上述三种模型给出的峰值加速度的估计非常接近，这是因为一般该震级-距离段内强震资料较为丰富，不同研究给出的估计大体相当；在更高震级处，由于五代图模型采用了分段线性的震级项，更多地考虑了震级饱和效应，因而得到的高震级段峰值加速度要低于另外两个模型.现今大多数研究均认为高频地震动存在震级饱和效应，五代图模型的结果反映了这一认识，表明其合理性.

图1 三种衰减模型峰值加速度在长轴（a）、短轴（b）方向的对比图Fig.1 Magnitude and distance scaling of the attenuation relationship of PGA for major axis （a） and minor axis （b） given by three models

图2给出了上述三种模型的5%阻尼比反应谱在长轴、短轴方向的对比图（M＝5，6，7，8，震中距R＝50 km）.从图中可以看出：在中等震级时，三者的结果十分相近，反映了在强震资料丰富段不同研究的结果趋于相近；在低震级时，五代图的结果基本位于二者之间；在高震级时，由于五代图模型更多地考虑了大震震级饱和效应，五代图的结果要低于另外两者的估计.从谱型上来看，随着时间的推移，更新的研究结果总体表现为反应谱越来越“窄”，即特征周期逐渐减小.另外需要注意的是，由于霍俊荣（1989）使用的数据集中有相当一部分属于模拟式记录，其长周期信噪比不高，因此长周期段存在不合理的翘起，在周期1 s附近存在鼓包，近期的研究结果使用了高质量的数字记录，谱型整体更加光滑，长周期段趋势更加合理.

宏观上来看，以上三套衰减关系的建立具有一些共性：模型上具有一致连贯性，均采用近场饱和因子和线性或者分段线性的震级项，联合反映大震近场距离、震级饱和效应；为了解决我国强震资料缺乏的问题，利用资料丰富的美国西部地区作为参考区，通过中国、美国丰富的烈度资料，采用转换修正的方式得到了我国各分区的衰减关系.随着时间的推移，更新的衰减关系无论是在数据资料的丰富程度和可靠性，还是在回归方法等方面，相较于前一代均有改进，反映了研究人员对于地震动参数特性的认识水平也在不断提高.

5 讨论

近数十年我国衰减关系研究进入高速发展阶段，取得了较为丰富的研究成果.但对于我国整体而言，我们认为仍然存在几个因素制约着衰减关系研究的进一步发展，简析如下：

其一，从总体上来看，我国强震台网建设的起步时间晚，强震记录的收集还远未达到丰富的程度.自2008年汶川地震以来，虽然在西南地区布设了大量强震台站，并获取了相当数量的强震资料，但是其中基岩台址的记录还是偏少；我国强震资料分布存在地区性差异，西南地区较为丰富，而华北地区近三十年未有大震，华中等中强地震区强震资料也不足.因此，具有工程意义的大震资料总体上还是相当匮乏，考虑到大震复发间隔长的因素，在未来可预期的时期内，这种状况还将持续.

其二，我国已有台站的台址信息仍略显不足，目前存有实际钻孔资料的强震台址数量偏少，较多台站仍使用简单的基岩或土层分类，不利于使用波速信息完成场地条件分析.如能对大批土层台站的波速信息进行较为精确的确定，则能够利用土层与基岩记录之间的换算，大大扩充基岩地震动估计时可用的强震资料库.

其三，我国目前的衰减关系研究更多的还是针对基岩场地，在工程应用上常使用土层反应分析计算土层效应.但是对于长周期地震动，浅表土层对于其的放大有限，更多的还是受深厚沉积层和大规模盆地的影响.我国华北、四川等几个大盆地沉积层深厚，人口稠密，高层建筑日益增多，面临较高的长周期地震风险.目前的衰减关系研究受强震资料所限，在该方面还略显不足.

因此，在已有成果的基础上，下一阶段如能持续推动基岩强震观测台站建设、缺乏强震动资料地区衰减关系建立新技术、与我国工程应用相衔接的场地效应模型建立新方法、宽频带高效强地面运动模拟与应用等方面研究，对我国整体地震动参数估计的发展必然能够发挥巨大的支撑作用.