基于贝叶斯推断的威布尔型产品可靠性评估

0 引言

以运载火箭、风电机组、新型装备等为代表的产品由于可靠性试验周期短，实验成本高，实验数据短缺，在对其进行可靠性评估等量化工作时面临小子样问题[1]。最大似然估计法等传统可靠性评估方法在面对小子样可靠性评估问题时容易产生较大偏差[2]。而贝叶斯推断能融合并利用各种先验信息（包括历史数据、相似产品数据以及专家经验）与试验信息，并用试验信息不断更新先验信息，最终得到可靠性评估模型中待估参数和可靠性指标的估计值与置信区间，能有效控制小样本数据带来的不确定性[3]。因此，贝叶斯推断在小子样可靠性评估中应用广泛。

在已有研究多集中于指数分布型产品或简化威布尔型产品的情况下[4-6]，对更一般双参数的威布尔型产品建立基于贝叶斯推断的可靠性评估模型。威布尔分布函数无共轭先验分布，假设待估参数服从Gamma分布[7]，保证其正定性，利用先验信息与专家经验确定Gamma分布中超参数，得到待估参数先验概率密度函数，结合似然函数生成后验概率密度函数，应用马尔可夫链蒙特卡洛法具体为NUTS抽样模拟待估参数的后验概率密度函数，求得待估参数估计值与置信区间。以某型号风力发电机齿轮箱的8次故障数据为算例，证明该方法的正确性与有效性，并完成对其可靠性评估。

1 贝叶斯推断

贝叶斯推断能将先验信息与观察到的故障数据相结合，以推断待估参数ξ（ξ1，ξ2，…，ξn）的数学特征。贝叶斯推断的核心是贝叶斯定理，贝叶斯定理可以实现通过收集到的数据y（y1，y2，…，yn）对已有信息更新[8，9]。如下所示：

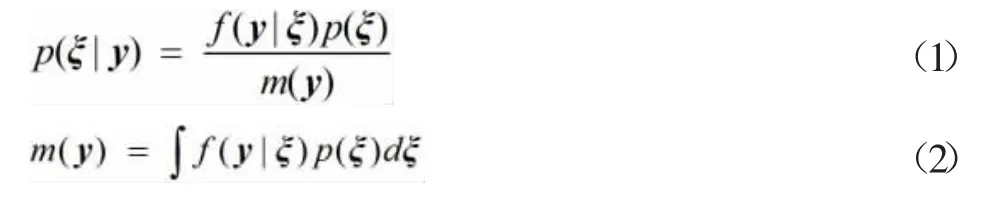
其中y（y1，y2，…，yn），表示观测到随机变量y的数据向量；p（ξ｜y）为后验密度函数；p（ξ）为先验密度函数；f（y｜ξ）为数据的抽样密度函数即似然函数；m（y）为数据的边缘密度函数。根据贝叶斯定理，后验分布可成比例表示为似然函数与先验分布的乘积，即

其中m（y）与参数ξ无关，被视为比例常数的一部分。获得观测数据前，对参数ξ（ξ1，ξ2，…，ξn）的信息集中于p（ξ），在获得观测数据y（y1，y2，…，yn）后生成似然函数，并更新生成后验分布。

1.1 Weibull分布

Weibull分布作为常用可靠性分析统计分布，对机械产品的故障时间数据拟合能力强[10，11]，故障时间t的概率密度函数为

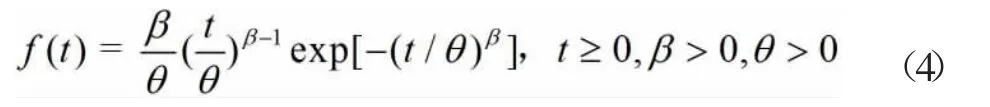
其中，β是形状参数；θ是尺度参数，也称为特征寿命。待估参数为β与θ。

可靠度函数为

累积分布函数为

平均故障间隔时间为

1.2 似然函数

对于故障时间T（t1，t2，…，tN），T~Weibull（θ，β），似然函数为各故障时间概率密度函数乘积，即

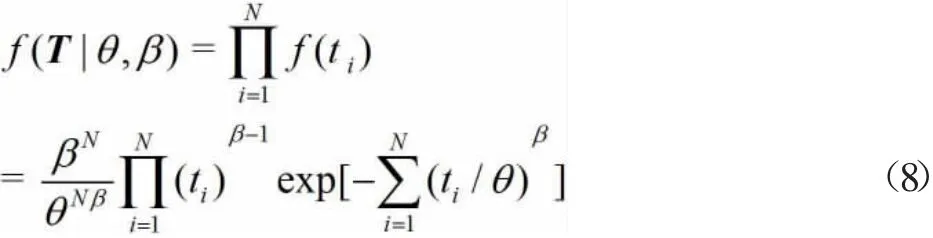
1.3 待估参数先验分布与后验分布

当Weibull分布的形状参数和尺度参数均未知时，不存在适用的共轭先验分布。对于θ与β，假设其先验分布为Gamma分布，且两个参数相互独立，即

θ~Gamma（α1，λ1），β~Gamma（α2，λ2）

α1，α2＞0为形状参数；λ1，λ2＞0为尺寸参数。对于超参数α1，α2＞0与λ1，λ2＞0可根据产品可靠性先验信息，以矩估计与专家经验相结合的方法求解。

此时θ概率密度函数（条件先验）为f（θ｜α1，λ1）=，均值对θ概率密度函数（条件先验）化简可得p（θ｜α1，λ1）∝θα1-1exp（-λ1θ）。θ条件后验密度函数为：

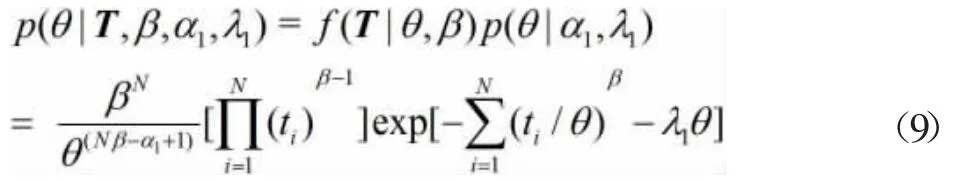
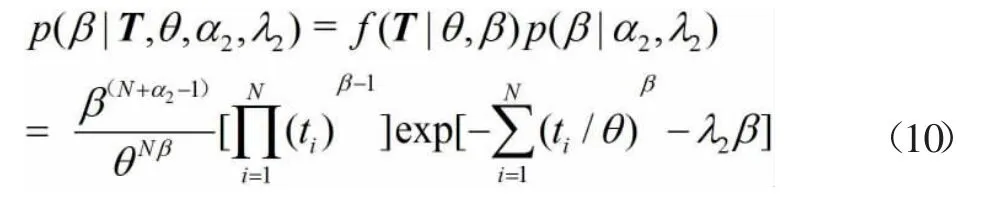
对于以上条件后验密度函数由于无法用解析方法求得，需要应用数值模拟方法—马尔可夫链蒙特卡洛方法[12，13]。

2 马尔可夫链蒙特卡洛法

马尔可夫链蒙特卡洛法（MCMC）也称为马尔可夫链蒙特卡洛抽样器，其将马尔可夫链与蒙特卡洛法相结合。其 中 马尔可夫链是指一系列随 机样本ξ（ξ1，ξ2，…，ξn），P（ξn+1｜ξ1，ξ2，ξ3，…，ξn）=P（ξn+1｜ξn）。即ξn+1取值只与当前取值ξn有关，而与之前取值无关。在马尔可夫链中相邻样本（ξi，ξi+1）之间可以发生转换，其转换概率P（ξi→ξi+1）由转换概率分布函数确定。在齐次马尔可夫链中，生成的样本分布将逐渐收敛，并趋于平稳[14，15]。在贝叶斯推断背景下，该平稳分布即为待估参数后验分布[16，17]。但马尔可夫链的初始样本并不来源于平稳分布，因此也不能代表该平稳分布，该过程称为老炼阶段（burn-in），应从马尔可夫链中剔除。

设老练期生成样本数Nburn-in，马尔可夫链生成总样本数N。当算法进行了Nburn-in次后，产生的仿真序列可以认为是来自后验分布的样本，而Nburn-in次之前的样本属于算法的老炼阶段，不能认为来自后验分布。因此，MCMC创造了一个马尔可夫链，该马尔可夫链的不变分布即为所求的后验概率分布。常用MCMC算法有Metropolis-Hastings算 法、Gibbs抽 样 与Hamiltonian蒙特卡洛方法[18]。其中Hamiltonian蒙特卡罗（Hamiltonian Monte Carlo，HMC）方法也称为混合蒙特卡罗（Hybrid Monte Carlo）方法，其采用系统动力学而不是概率分布来建议马尔可夫链中的未来状态，使得马尔可夫链能更有效地探索目标分布从而实现更快的收敛。无掉头抽样器（No-U-Turn Sampler，NUTS）作为HMC的拓展，使用成对平均算法[19]，可以在完全不进行任何手动调整的情况下运行，生成的样本至少与精细的手动调整HMC一样。

对威布尔型产品，参数向量中包含2个元素（θ，β），由1.3节知每个元素的条件后验分布为p（θ｜T，β，α1，λ1），p（β｜T，θ，α2，λ2）。

3 算例分析

以某型号风力发电机齿轮箱的8次故障数据为算例[20]，验证上述可靠性评估模型。风电机组齿轮箱故障状态 数 据（4707，6167，9887，9991，13712，16543，18007，20793），均为停机故障，单位：时。使用最小二乘法计算得到，θ=19000，β=2.3。

对于先验分布，应用矩估计法并借助专家经验，可确定以下方程式：

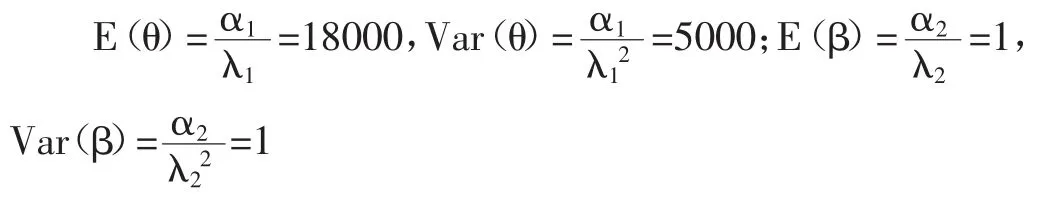
解得，λ1=3.6；α1=64800，λ2=1，α2=1。将结果代入θ条件后验密度函数与β条件后验密度函数。

3.1 NUTS抽样

采用基于Python平台的PyMC3进行NUTS抽样，仿真环境为PyCharm Edu，抽样次数设置为5000次，Nburn-in=1000，抽样结果如表1所示。

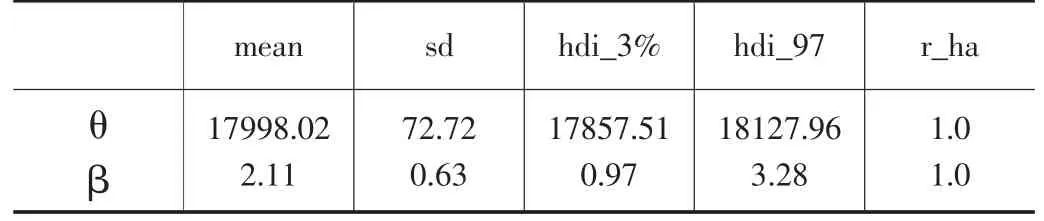
表1 NUTS抽样结果

即θ后验均值17998.02，标准差72.72；β后验均值2.11，标准差0.63。

生成后验密度直方图和最高密度区域图如图1。

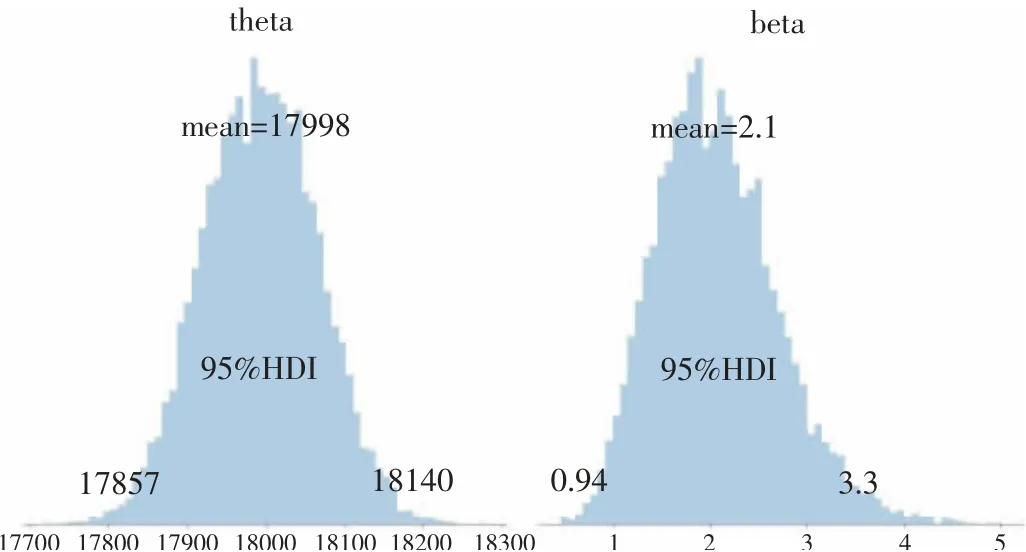
图1 θ、β后验密度直方图与最高密度区域

生成密度估计图和痕迹图如图2、图3。

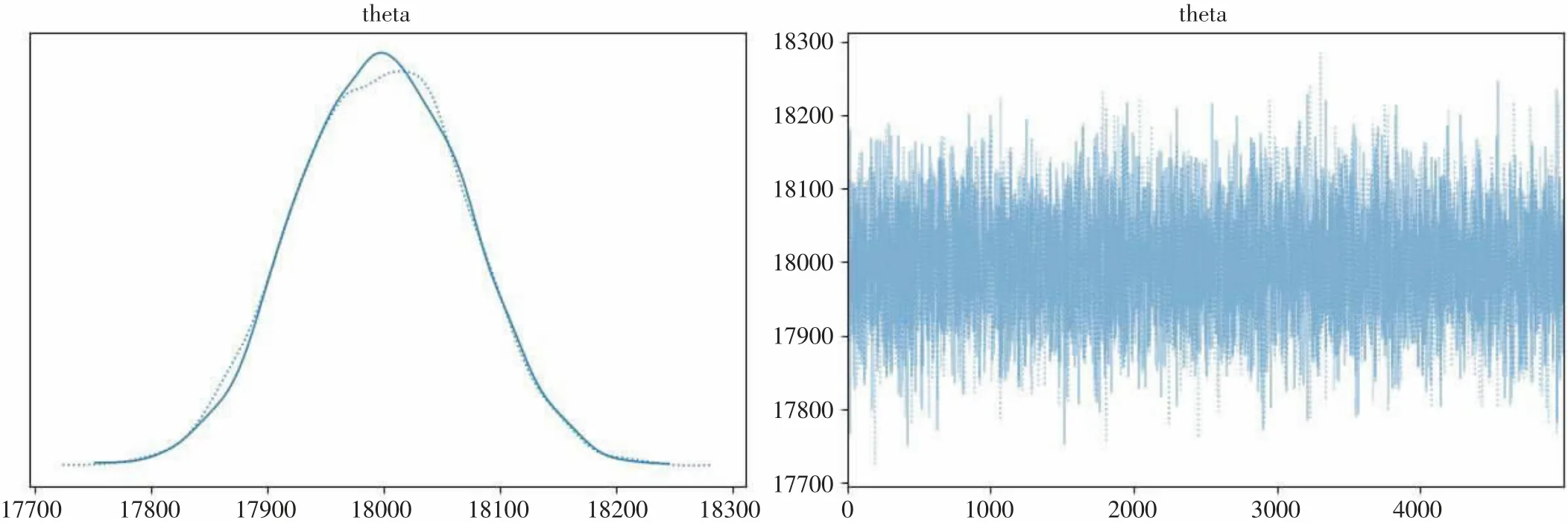
图2 θ密度估计图和痕迹图

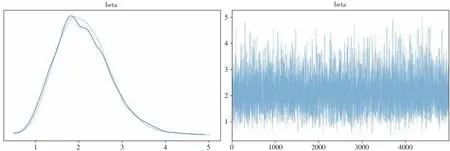
图3 β密度估计图和痕迹图

3.2 结果分析

文献[20]分别使用最小二乘法根据8次故障停机数据及文献改进方法根据8次停机故障数据加12次非停机故障数据对双参数进行估计，结果如表2所示。

表2 三种方法参数估计对比

通过对比可知，提出基于贝叶斯推断的威布尔型产品可靠性评估方法在利用8次停机故障数据情况下，估计所得θ均值介于最小二乘法与文献[20]改进方法。在可利用故障数据一致情况下，本文方法得到的尺度参数θ估计值比最小二乘法更精确，相较文献[20]方法更加合理。对于形状参数β，估计值大于1，说明失效率随时间增加，根据本文方法得出的故障规律与最小二乘法、文献[20]改进方法一致。

通过生成抽样能量图，可以看出能量（Marginal Energy Distribution）及能量转换（Energy Transition Distribution）两个分布范围接近，宽窄相近，说明NUTS抽样中失去的信息不重要，后验估计准确。

3.3 可靠性评估

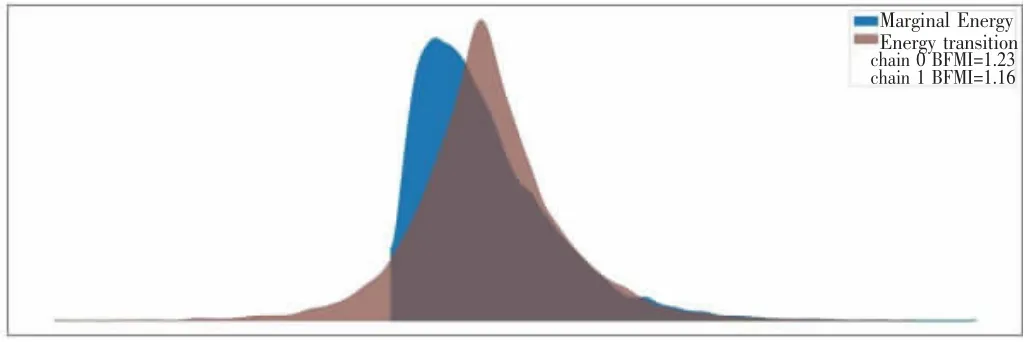
图4 抽样能量图

将NUTS抽样产生的形状参数与尺度参数带入可靠性评估模型（4）（5）（6）（7），可得故障时间t的概率密度函数为：

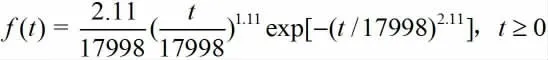
可靠度函数为：

R（t）=exp[-（t/17998）2.11]

累积分布函数为：

F（t）=1-exp[-（t/17998）2.11]

平均故障间隔时间为：

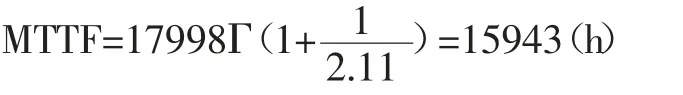
由上述可靠性模型计算得出某型号风力发电机齿轮箱的平均故障间隔时间为15943h，完成了可靠性评估。

4 结论

本文针对更一般的双参数威布尔型产品建立基于贝叶斯推断的可靠性评估模型，在无共轭先验分布情况下，均假设其待估参数服Gamma从先验分布，推导出待估参数后验概率密度，而非简化为指数分布型可靠性模型。充分利用已有数据与专家经验，应用MCMC法中NUTS抽样求解待估参数点估计值与置信区间，实现复杂密度函数的仿真模拟。经过算例分析可知该模型的输出结果正确可靠，既扩大贝叶斯推断的应用范围又能保证求解精度。模型通过调整先验分布可以求解不同威布尔型产品的待估参数与可靠度函数，具有可重用性。对于不同威布尔型产品，借助先验信息与专家经验确定待估参数先验分布后，通过修改PyMC3中参数信息，可用于求解待估参数，有助于对小子样产品的可靠性评估与可靠性管理。

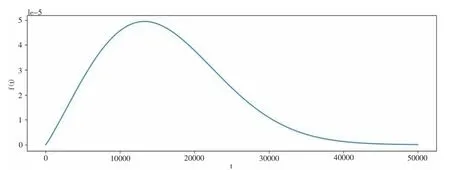
图5 故障时间概率密度函数

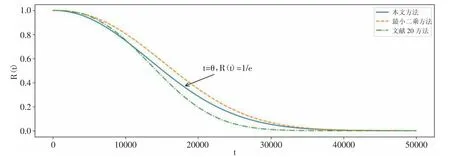
图6 可靠度函数

在本文基础上，可以进一步研究融合多源数据的基于贝叶斯推断可靠性评估，量化专家经验控制主观性，充分利用各种先验信息，进行更准确的小子样产品可靠性评估与优化。