无轴承薄片电机位移刚度势能悬浮控制策略研究

丁强，江莹旭，倪拓成

（1.南京工业职业技术大学电气工程学院，江苏南京 210023；2.江苏省风力发电工程技术中心，江苏南京 210023；3.苏州新智机电工业有限公司，江苏苏州 215000）

无轴承永磁薄片电机（bearingless permanent magnet slice motor，BPMSM）作为一种磁悬浮特种电机，具有无机械磨损、无需润滑、寿命长的特点，在超洁净场合（如半导体清洗、食品化工、生命医疗等）有着广泛的应用前景[1-3]。

BPMSM的轴向尺寸较短，一般仅为转子直径的1/3～1/4，因此可以利用永磁体产生的磁阻力实现转子在轴向平移方向和扭转方向的被动稳定悬浮。但其径向自由度是被动不稳定的，需要通过在绕组中注入悬浮电流主动控制径向力，实现转子在径向的二自由度悬浮[4]。因此，无轴承薄片电机悬浮控制对系统的鲁棒性和安全性尤为关键。

针对无轴承电机悬浮系统的控制，不少学者基于现代控制理论、非线性控制理论等提出了各种优化控制算法。文献[5]针对悬浮控制磁链精度不足的缺陷，采用基于锁相环原理的磁链观测器算法。文献[6]为解决转矩和悬浮力之间的耦合问题，将神经网络的思想引入无轴承的控制中。除此以外，直接悬浮力控制[7-9]、自抗扰控制[10-12]也是学界研究的热点。尽管如此，PID控制由于算法实现简单，仍然是无轴承悬浮控制中应用最为广泛的控制器。

然而在实际悬浮系统调试过程中，由于位移环PID参数整定过程缺乏理论指导，确定一组既能保证悬浮系统系统稳定，又能满足动静态悬浮性能需求的参数，通常需要较多时间尝试。针对此问题，本文对悬浮控制PID参数的稳定域范围进行了理论探究。在此基础上，本文进一步分析了微分环节滤波对悬浮系统稳定裕度的影响，指出PID控制所存在的问题，为工程实践提供了指导。

为了进一步改善悬浮系统动态和稳态性能，本文提出一种基于转子位移刚度势能控制的算法，该算法使转子处于低势能位时可以以最快的速度向平衡位置运动，在高势能位时，以无超调的运动状态到达稳定位置，兼顾了动态和稳态性能。本文用理论推导证明了方案的可行性，并通过仿真和实验验证了算法的有效性和鲁棒性。

1 电机结构及径向力模型

以图1所示6齿1对极单绕组无轴承永磁薄片电机为例，推导建立电机径向悬浮力数学模型。

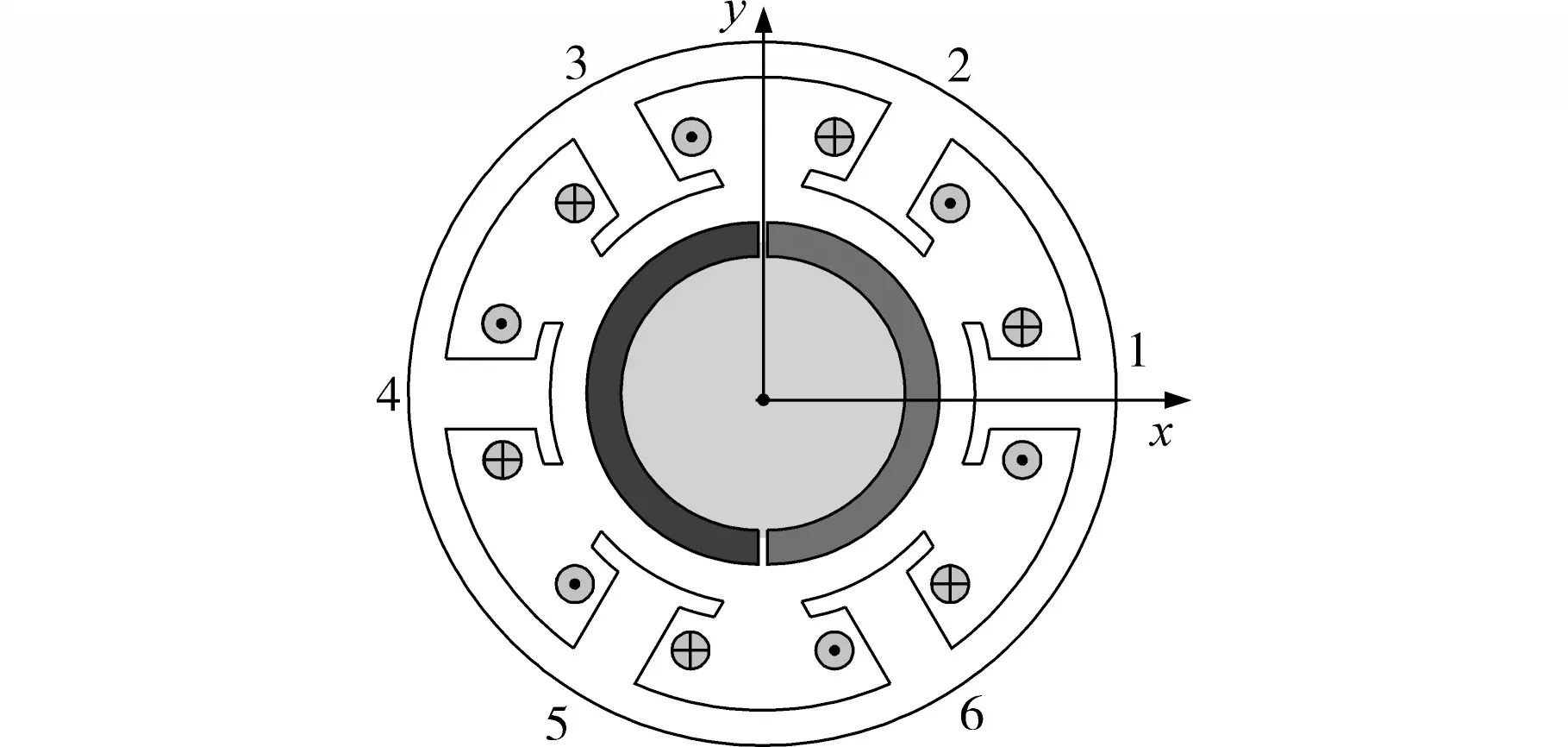
图1 单绕组无轴承永磁薄片电机Fig.1 Single-winding BPMSM

从产生转矩的角度来看，此电机可以看成六相电机，假设各相转矩电流为

式中：At，θt分别为转矩电流的幅值和相位；n为绕组编号（n=1，2，…，6）。

若电机转矩控制采用直轴电流id=0的矢量控制算法，则转矩电流相位θt始终超前转子相位90°。

基于式（1）转矩电流表达式，为了满足悬浮磁场与转矩磁场极对数相差1对极的基本原理，各相绕组中悬浮电流可以表示为

式中：Al，θl分别为悬浮电流的幅值和相位。

利用磁场叠加原理，通过麦克斯韦力的方程可推导电机径向悬浮力数学表达式为[13]

式中：μ0为真空磁导率；r，h，leg分别为电机转子的外半径、轴向长度以及等效气隙长度；α为电机定子齿的极弧宽度；APM为电机转子永磁体的磁势幅值；θr为电机转子机械转角；lpx，lpy分别为电机转子在径向x，y方向上的偏心距离。

分析电机径向力模型可知，转子的径向受力由两部分构成，第一部分与悬浮电流的幅值和相位有关，此部分是通过注入悬浮电流实现的主动控制部分。第二部分与转子的偏心位置有关，由于leg通常变化较小并且APM＞＞At，因此系数kxx和kyy可近似认为是常数，后文中统一表示为ks。由此可以看出，第二部分径向力正比于转子的偏心位移，并且其作用方向总是指向偏离平衡位置的方向，因此该力是无轴承电机悬浮系统中的不稳定因素，称之为径向被动刚度力。通常意义上，本文所述的悬浮力指的是第一项由悬浮电流产生的径向力，只要控制悬浮电流的幅值即可控制悬浮力的大小、控制悬浮电流的相位，即可控制悬浮力在x，y轴上的分量，也即控制力的方向。

2 位移环PID参数整定及其问题

在不考虑径向力负载或扰动的情况下，无轴承电机位移环结构如图2所示，sref为参考位移，一般设定为零；m为转子质量；ks为转子的位移刚度系数；kp，ki，kd分别为PID控制参数；Td为微分环节的滤波时间。

图2 无轴承电机位移环路传递函数Fig.2 Displacement loop transfer function of BPMSM

根据图2可以写出系统的开环传递函数为

暂时不考虑微分项的滤波时间，则表达式可写为

对应的闭环传递函数为

系统的特征方程为

根据劳斯判据不难得出悬浮系统稳定的充要条件为

式（10）给出的仅是无轴承电机悬浮系统稳定的基本条件。为了能满足一定的悬浮性能要求，需要对PID参数作进一步约束。从闭环传递函数的特征方程可以看出该系统是三阶系统，存在三个极点。为了兼顾动态和稳态的性能，将其中一个极点分配在负实轴上，另外两个为共轭的主导极点，则特征方程可写成如下形式：

式中：z0为位于实轴的极点；ξ，ωn分别为二阶环节的阻尼比和角频率。

将式（11）对比式（9）可以得到：

考虑到共轭极点对性能起到主导作用，将非主导极点（-z0，0）到虚轴距离配置为共轭极点到虚轴距离3倍以上，则有：

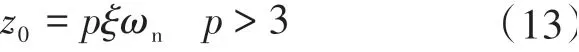
式中：p为系数。

至此，可以根据式（12）、式（13）对PID参数进行约束。为了兼顾动态性能和稳态性能，ξ和p分别取0.707和5。由此可将三个参数的自由度约束为关于kp系数的整定。

图3为kp不同取值时的阶跃响应曲线。由图3可以看出，kp系数越大，系统的动态性能越好。相应的，整定的kd也会越大。无轴承电机悬浮控制实践表明微分环节会引入噪声，导致系统稳定裕度降低。因此需要根据位移反馈信号的噪声条件，限制微分系数的大小，并且在微分环节上加入小滤波环节来改善信噪比。但是，滤波环节的引入对系统稳定性的影响却未能得到足够的重视。

图3 不同kp取值下的阶跃响应Fig.3 Step response of different kp

图4为kp取5倍ks的情况下，根据上述的参数整定结果，选取不同的Td绘制波特图。当Td=0时，系统的稳定性较强，相角裕度有90°。加了滤波环节后，系统的相角裕度显著减小，即便Td取值仅有10-5，相角裕度也已经降低到20°以内，当Td取值超过5×10-4时，相角裕度已经非常接近零，此时系统已经濒临不稳定。显然，在存在Td的情况下，原整定的参数已经较难稳定，则需要再一次进行调整，改善系统的稳定裕度。

图4 不同Td取值下的波特图Fig.4 Bode diagram of different Td

图5为滤波系数Td取0.001时，在初始整定参数的基础上调整微分系数绘制波特图。可以看到，微分系数可以提高相角裕度，但微分系数减小会牺牲系统的响应带宽。当kd降低到初始值kd0的0.01时，相角裕度反而出现了轻微的下降，此时降低微分系数不仅牺牲了带宽，还降低了稳定性能。

图5 不同kd取值下的波特图Fig.5 Bode diagram with different kd

综合上述分析，可以归纳无轴承电机悬浮系统位移环PID控制存在如下问题：

1）悬浮系统动态性与稳定性的矛盾。kp越大系统动态性能越好，但同时需要的kd越大，则导致信噪比降低，系统稳态性受到影响。

2）悬浮系统信噪比与稳定性的矛盾。增加惯性滤波环节Td可提高信噪比，但会降低系统稳定裕度。同样，减小kd也可以提高信噪比，但同样降低稳定裕度。

考虑到微分环节滤波的影响，应根据实际信号的信噪比，选取尽可能小的微分滤波系数，并在此基础上适当调整微分系数以获得更好的稳定裕度。

3 位移刚度势能悬浮控制

上一节分析了无轴承电机悬浮系统位移环PID参数整定及其存在的固有问题。由于PID算法是基于线性调节器理论进行设计的，在无轴承电机悬浮系统控制实践中，由于噪声、滤波环节等因素的存在，转子的稳定裕度和实际的位移响应并非如预期的理想，实际中总是存在震荡超调等问题。

无轴承电机悬浮控制的基本目标为，当电机转子偏离中心时，系统可以有较快的速度回到中心平衡位置，并且位移控制的超调量要尽可能小。同时，悬浮系统需要对给定量有着较好的跟踪性能，在转子受到扰动偏离中心平衡位置时具有较好的鲁棒性。现代控制理论已经证明，采用开关控制，也即Bang-Bang控制，是一种时间最优的控制方案。当偏电机转子位移偏离中心平衡位置时，转子回复到平衡状态的时间最短、动态性能最优。但是，当转子处于中心平衡位置或者中心平衡位置附近时，传统Bang-Bang控制的机理决定其所输出的悬浮力在限幅边界处来回切换，导致转子始终处于振动状态。为解决上述问题，本文提出了基于位移刚度力场势能的悬浮控制算法。

当电机转子处于自由状态时，也即没有可控悬浮力和其他外力作用时，转子仅受到位移刚度力的作用。如式（3）所示，该力正比于转子偏离平衡位置的位移。类比于重力势能的概念，转子在位移刚度力场的作用下，也具有对应的势能，称之为位移刚度势能。如果将平衡位置的势能定义为0，则位移刚度力势能Es和位移s之间的关系满足式（14），其曲线如图6所示。

图6 位移刚度力场下的转子势能Fig.6 Rotor potential energy in stiffness force field

由图6势能曲线可以看出，当悬浮系统无可控悬浮力作用时，无轴承电机转子径向自由度为不稳定系统，转子在中心平衡位置O的势能最大，因此当电机转子受到外部扰动便会向势能低的位置运动且无法自发的回到稳定位置。

电机转子机械能可以表示为刚度势能和动能EV之和，即

式中：s0，v0分别为初始时刻转子的位置和速度。

由于无轴承电机悬浮控制目标是将转子控制在中心位置并且静止，从能量角度需要满足：

假设k时刻转子的位置和速度状态分别为sk和vk，其总机械能为ET0。系统的末状态的速度和位移均为零，根据能量守恒定律：

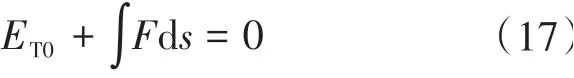
式中：F为悬浮力。

写成离散的形式即为

受悬浮绕组载流量的限制，控制量悬浮力的作用边界如下：

式中：Fmax为悬浮力的最大值。

刚度势能控制过程如图7所示。

由图7可知，在k时刻需要计算悬浮力输入给转子的能量，也即悬浮力Fk与位移差值Δsk+1（Δsk+1=sk+1-sk）的乘积。为使得系统的能量尽快归零，每拍输入的能量应尽可能多，但当转子的能量满足：

表明k时刻悬浮力即使作用到最大，也无法令转子等效势能立即归零。

因此当转子能量较低时，可以让悬浮力处于作用域[-Fmax，Fmax]的边界上，此时等效势能便会以最快的速度增加，其控制效果和Bang-Bang控制等同。当电机转子能量增加，较为接近零势能点时，如图7中k+n时刻，计算需要给定的悬浮力满足：

表明此时需要输出的悬浮力处于作用域内，经过该力一拍的作用，系统能量可精确归零，不存在超调，解决了Bang-Bang控制在平衡位置附近造成的控制量变化巨大引起转子震动的问题。

可以看出，上述每个时刻计算输出悬浮力时均需知道在该悬浮力作用下的位移Δsk+1，从而计算出在该时间段内输入给转子的能量。电机的运动状态方程如下：

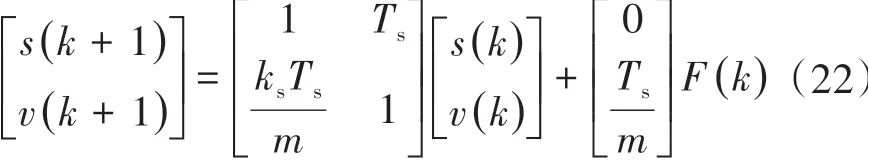
式中：Ts为控制周期。

可以根据本拍转子状态预测出下一拍转子位移sk+1。将其与本拍位移sk作差后可计算出Δsk+1。

4 径向负载观测器

以上基于位移刚度势能的控制算法避免了传统PID控制中参数整定困难的问题，在继承Bang-Bang控制动态性能优势的基础上，提升了电机转子在中心平衡位置附近的控制性能。然而，以上推导均基于无其他径向力的前提。实际上，无轴承电机悬浮系统中除了位移刚度力和可控悬浮力之外，往往还存在径向的负载力、转子质量不平衡引起的偏心力等，这些径向力的作用将使得每个控制周期内输入到转子的能量产生偏差，导致转子无法稳定在能量最高处。针对此问题，有必要对转子受到的径向负载进行观测并补偿，以此消除其对中心平衡点的影响。

考虑径向负载力时，无轴承电机转子的径向运动学状态方程可以写成：

式中：fd为径向负载力。

根据现代控制理论，可在控制器中构建一个与式（23）相同的状态观测器。但受到参数失配和扰动的影响，实际系统的输出和观测器的输出并不完全相同，因此可以将实际系统和观测器的输出量作差后，反馈到观测器的输入端，由此观测器的输出和实际系统输出间的误差将收敛至零。当观测器带宽足够高时，收敛速度便足够快，此时可将观测器中的状态作为实际系统的状态用于状态反馈，观测器结构如图8所示，其中H为反馈矩阵。

图8 状态观测器结构框图Fig.8 Block diagram of state observer

根据上述原理，可写出状态观测器表达式：

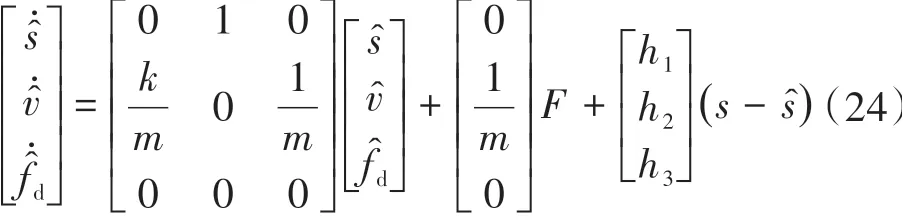
依据式（24）并按照图8观测器结构，可以得到适用于无轴承电机悬浮系统径向负载力的观测器。在此基础上，图9给出位移刚度势能悬浮控制的结构框图。

图9 位移刚度势能悬浮控制结构框图Fig.9 Block diagram of the displacement stiffness potential energy suspension control system structure

5 仿真与实验

为了验证本文所提的位移刚度势能悬浮控制算法的有效性，本文在Matlab/Simulink中搭建的仿真模型并编写实验控制程序，通过和传统PID控制对比，验证该悬浮控制算法的有效性。依据图9所示，悬浮系统中转子能量给定量设为0，由式（15）计算转子实际能量并于转子能量给定量做差后，经刚度势能控制算法调节得到悬浮力给定值。将悬浮力给定值减去由径向负载观测器观测得到的径向负载力后，对转子施加实际控制作用。

仿真与实验中电机的主要参数如下：定子外径146 mm，定子内径84 mm，定子齿极弧40°，转子外径78 mm，转子质量192 g，轴向长度10 mm，永磁体厚度3 mm，径向刚度23 N/mm。

图10对比了没有径向外加负载力的情况下，转子从偏心1 mm位置从静止状态起浮波形。由图10可知，初始时由于转子位移s偏心较大、能量较低，此时等效为Bang-Bang控制，相比PID控制，其动态响应更快；当转子位移靠近平衡位置时，电机转子位移刚度势能接近零，此时控制量输出变小，因此牺牲了一定的动态性能，以获得较优的稳态性能，整个过程中位移无超调。总体而言，刚度势能控制算法在动态性能上仍优于PID控制。

图10 无径向负载力静止起浮位移仿真波形Fig.10 Simulation waveforms of start-up displacement without radial load force

图11对比了在径向阶跃负载工况下的位移刚度势能控制和传统PID控制。

图11 有径向负载力静止起浮位移仿真波形Fig.11 Start-up displacement simulation waveforms with radial load force

由图11b可知，负载观测器在3.5 ms跟踪上了实际径向力，经过补偿后，位移刚度势能控制对负载力有了较好的响应，由图11a可知其位移仅波动20 μm。相比之下，PID控制器需要经过25 ms的调节时间才能稳定并且在径向负载力作用下位移波动达到了42 μm。

在仿真验证的基础上，本文搭建了无轴承薄片永磁电机的实验平台进一步对算法有效性进行验证。图12为实验中所用无轴承薄片永磁电机原理样机。

图12 无轴承薄片永磁电机原理样机Fig.12 Prototype of BPMSM

为了验证微分环节中滤波系数对系统稳定性的影响，图13对比了在相同PID参数下，不同的滤波时间常数下的起浮波形。

图13 转子起浮的位移波形Fig.13 Rotor displacement waveforms when start-up

由图13a可知，当无滤波环节时，起浮的动态过程中，转子位移表现出了良好的阻尼特性。然而由于位移反馈信号在处理环节中不可避免会引入噪音，稳态时，转子仍然存在抖动。由图13b可知，加入了1 ms的滤波环节后，起浮的动态过程中，虽然出现了小幅的超调，但稳态波形较无滤波环节时有了显著改善。由图13c可知，当滤波时间增加到5 ms后，由于滤波环节产生的信号延迟，转子震荡时间明显增加，系统的稳定裕度减小。因此综合考虑，PID控制的微分滤波时间取1 ms较为合适。

为了对比PID控制和位移刚度势能控制在动态性能上的差异，图14对比了在相同的径向冲击扰动下的转子位移波形，径向扰动力主要施加在y的正方向。

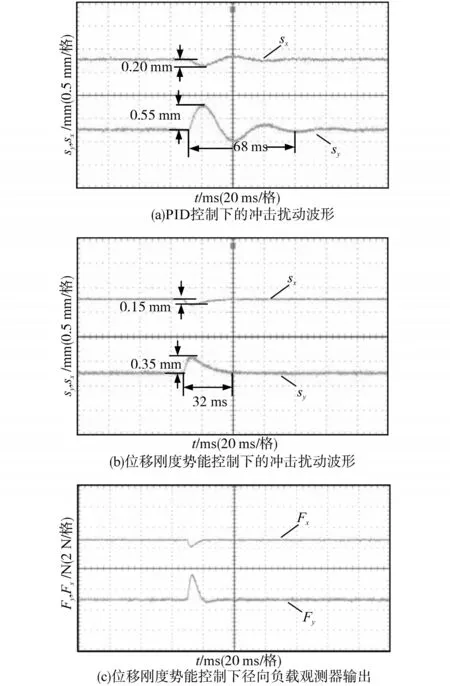
图14 转子冲击扰动下的位移波形Fig.14 Rotor displacement waveforms under impact loads

由图14a可知，PID控制下，两个自由度的位移的波动达到了0.20 mm和0.55 mm，调节时间大约为68 ms。由图14b可知，采用了位移刚度势能控制时，由于引入了较强带宽的负载观测器，并且在大位移时，悬浮力等效为Bang-Bang控制，位移波动仅为0.15 mm和0.35 mm，大大改善了径向位移环路的鲁棒性。除此之外，由于控制器实时计算了转子的刚度势能，本质上对转子的运动状态有了一定的预测作用，因此调节之间大大缩短，仅有32 ms。同时图14c给出外部冲击扰动作用时径向负载观测器的输出信号。

图15为电机在3 000 r/min情况下PID控制和位移刚度势能控制的稳态位移波形。由图15a可知，PID控制下x轴的位移波动约为±45 μm，y轴的位移波动约为±50 μm；由图15b可知，刚度位移势能控制下x轴的位移波动约为±25 μm，y轴的位移波动约为±30 μm。

图15 3 000 r/min时转子的位移波形Fig.15 Rotor displacement waveform when 3 000 r/min

6 结论

本文针对无轴承薄片永磁电机悬浮系统位移环PID控制参数问题进行理论推导和分析并指出其PID控制的固有问题。结果表明，PID三个参数需要满足特定的约束关系悬浮系统才能稳定，其中微分系数是系统稳定的重要环节。但微分环节中的滤波对系统稳定性是不利的因素，需要根据信号的噪声情况，适当牺牲带宽来换取较高的稳定裕度。为克服PID控制的不足，文章提出了转子位移刚度势能的非线性悬浮控制算法，该算法兼顾转子势能较低处的动态性能和势能较高处的稳态性能，并通过负载观测器补偿了其他径向力对转子势能的干扰，可快速将转子控制在平衡位置。最后，通过仿真和实验分别验证了该算法的可行性和有效性。