基于离散动态事件树的风险指引的安全裕度分析方法研究

陈 妍，李朝君，张 盼，赵传奇，郑 洁，韩 治，李 春，依 岩

(生态环境部 核与辐射安全中心，北京 102400)

2012年，美国爱达荷国家实验室(INL)发布了轻水堆可持续发展项目的综合计划[1]，以响应美国能源部核能办公室2010年发布核能研发路线图中的目标“开发能够提高可靠性、维持安全性和延长现有反应堆寿命的技术和其他解决方案”。综合计划中给出4个研发方向：核材料老化和退化、先进轻水反应堆燃料开发、先进仪控技术以及风险指引的安全裕度特性(RISMC)分析技术。RISMC分析技术的目的是量化安全裕度，尽可能使安全裕度最优化以及不确定性最小化，进而保障轻水堆在运期间(尤其是延寿期间)的安全性和经济性都在高的水平。RISMC分析技术的计算方法是采用现有知识产生一系列基于风险的情景，利用系统模型计算系列情景下的特定安全性能参数，然后比较分析各情景下安全性能参数负载和能力分布的关系，最后统计计算系列情景下安全性能参数的负载大于能力的概率。本质上，RISMC分析技术是一种计算式的风险评估(CRA)方法[2]，其集成分析一系列概率情景及情景下的物理参数信息，这种多情景计算式方法可能对现有核电站的某些安全问题提出新的解决方案。

目前美国INL已基本建成了RISMC的计算平台，并开展了试点案例的分析计算[3-4]。法国电力研究所[5]、韩国原子能研究所等机构陆续开展了有关风险指引的安全裕度研究，我国近几年也开展了有关风险指引的安全裕度分析方法的研究[6-9]。但整体上，风险指引的安全裕度分析的案例尚少，其理论方法及实践分析需进一步深入研究和完善。离散动态事件树(DDET)是RISMC中产生风险情景的常用方法之一，本文研究基于DDET的风险指引的安全裕度分析方法，针对简化压水堆模型下的全厂断电事故，利用Python和系统热工水力程序计算两种DDET分支规则下的燃料包壳失效的风险指引的安全裕度及其不确性，然后探讨分支规则、模型参数分布、系统程序内置参数设置对燃料包壳失效的风险指引的安全裕度的影响，进一步提出一种改进的可变概率阈值的分支方法，以更好地平衡风险指引的安全裕度分析过程中的计算精度与计算资源的匹配问题。

1 基于DDET的风险指引的安全裕度分析方法

1.1 风险指引的安全裕度分析方法

裕度有确定性裕度和概率性裕度两种表征方法。确定性裕度通常定义为安全变量的能力(Capacity)与负载(Load)的差值或比值，概率性裕度通常定义为负载超过能力的概率。目前核电站中的安全分析大多数采用确定性裕度表征安全裕度，而风险指引的安全裕度分析技术采用概率性裕度来量化安全裕度，是近十年来核工业界提出的新的安全理念，其期望通过量化的概率性裕度避免不必要的保守性，为核电站延寿、长期运行以及扩展功率等有关安全裕度的管理决策提供必要的技术支持。

风险指引的安全裕度分析框架如图1所示，其利用失效模式、运行规则等信息产生各种情景以及相应的情景参数，然后将各情景参数传递给系统程序(如物理、热工等系统程序)，系统程序计算的过程物理参数也动态反馈给情景进行分支，最后计算出任务时间内各种情景下安全变量特性及情景概率，并用统计计算安全变量的安全裕度及其不确定度，进一步做出管理决策。风险指引的安全裕度的计算在具体实现时，需要通过搭建计算平台或开发计算程序，编程自动产生各种情景参数，计算每个情景的发生概率，采用系统程序计算每个情景下的重要物理/热工参数数值，并判断每个情景下计算的重要参数是否失效及计算每个情景下条件失效概率，最后统计计算风险指引的安全裕度用于管理决策。需要指出的是，风险指引的安全裕度分析方法中的安全变量需根据特定问题设置(如燃料包壳温度、燃料包壳应力、燃料包壳氧化物厚度等)。此外，风险指引的安全裕度也称为概率安全裕度[4]。目前风险指引的安全裕度分析方法中常用的情景产生方法有蒙特卡罗抽样方法、DDET方法、混合蒙特卡罗动态事件树等。本文研究基于DDET的风险指引的安全裕度分析方法。

图1 风险指引的安全裕度的分析框架Fig.1 Framework of risk-informed safety margin analysis

1.2 基于DDET的风险指引的安全裕度的量化

DDET是一种在离散时间轴上模拟和追踪系统在其任务时间内的所有可能的系统状态演化轨迹的方法，能够给出系统的连续变量与离散变量(硬件状态、人因干预等)之间随时间的演变。假设某系统状态由n个离散变量描述，分别设为k1，k2，…，kn，同时系统有m个连续参数变量，分别设为x1，x2，…，xm，t时刻系统的状态可表示为S(Kt，Xt，t)，其中Kt=(k1，k2，…，kn|t)为t时刻系统离散变量取值组合，Xt=(x1，x2，…，xm|t)为系统在t时刻各连续变量的取值组合，初始时刻系统的状态为S(K0，X0，t)，则连续变量与离散变量之间的关系满足微分方程：

(1)

其中：X为系统的连续变量；fKτ为τ时刻离散变量为Kτ的微分方程；Kτ为τ时刻的系统离散变量。Xt=gKτ(t-τ,Xτ)为式(1)的解，表示τ时刻系统的离散变量和连续变量分别为Kτ和Xτ，经历了t-τ时间后，系统的连续变量变为Xt。DDET的工程应用建模示意图如图2所示，即由离散变量在特定时刻产生分支，利用系统方程得到在时刻t系统的连续变量Xt，同时利用各分支节点处的概率可得到Xt的概率。因此，DDET能够模拟系统在任务时间内的所有可能的系统状态并给出所有系统状态概率的特性，满足风险指引的安全裕度分析的计算需求。

图2 DDET工程建模示意图Fig.2 Schematic diagram of DDET modeling

本文研究基于DDET的压水堆燃料包壳温度这一连续安全变量的风险指引的安全裕度。假设DDET方法下任务时间内产生n个事故情景，每个事故情景的概率为pi，每个事故情景下燃料包壳温度的计算值为xi，则每个情景下的燃料包壳失效概率yi为：

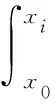
(2)

(3)

燃料包壳失效概率的样本标准差s为：

(4)

式(3)计算的燃料包壳失效概率均值即为一系列事故情景下的燃料包壳温度的风险指引的安全裕度，燃料包壳失效概率的样本标准差定量表征了燃料包壳失效概率的不确定性。值得注意的是，在风险指引的安全裕度分析方法中，研究对象和问题不同，安全变量的风险指引的安全裕度数学表达式也会有差异，具体分析中需要根据特定的研究问题给出特定的风险指引的安全裕度计算方法。

2 全厂断电事故的风险指引的安全裕度分析计算

2.1 热工模型及计算假设

参考INL在RISMC研究中有关简化压水堆模型下全厂断电事故(SBO)参数[10]，本文建立了简化核电站的热工水力模型节点图，如图3所示，其模化了反应堆压力容器的下降通道、下封头、堆芯和上腔室，堆芯部分的3个平行的燃料通道和1个旁通通道，两个主环路(每个环路由热管段、1个热交换器及其二次侧管段、冷管段和1个主泵组成)以及稳压器。本文建模假设与INL的建模假设存在不同：1) 本文假设主泵惰转，而INL假设电站发生SBO后主泵转速立即为0，应急柴油机(DG)恢复后，主泵又有一定转速；2) 冷却剂流量、换热器面积少量参数不同。

图3 简化核电站的节点示意图Fig.3 Node diagram of simplified nuclear power plant

在此简化压水堆模型下，SBO事故的情景是200 s的瞬态开始，201 s厂外电丧失，核电站立即停堆，随后主泵惰转，DG失效，造成冷却系统不可用，丧失热阱。假设DG的恢复时间(单位为s)服从正态分布Normal(2 900，200)，若DG在t时刻恢复，冷却系统可用。此外，假设燃料包壳失效温度(单位为K)服从Triangular(1 255.37，1 477.59，1 699.82)的三角分布[11]以及任务时间为3 600 s。

2.2 计算流程

为计算一系列事故情景下核燃料包壳失效的风险指引的安全裕度，本文提出基于DDET的风险指引的安全裕度的计算流程，如图4所示，其中关键参数是DG的恢复时间t，用于产生不同的事故情景，采用Python程序及树结构产生事故情景分支，并调用系统热工水力程序计算每个情景下的燃料包壳温度，最后统计计算核燃料包壳温度超过燃料包壳失效温度的概率及其不确定度。鉴于本文关注DDET方法对计算结果的影响，因此选择了简化的事故情景进行风险指引的安全裕度分析，即计算中只考虑DG在不同恢复时间的需求失效，暂不考虑外电网和辅助电网在不同恢复时间的需求失效，也不考虑核电站其他系统的随机失效以及人误事件等。

图4 基于DDET方法的风险指引的安全裕度计算流程Fig.4 Calculation process of risk-informed safety margin based on DDET

2.3 两种常用DDET分支规则下的风险指引的安全裕度分析

采用DDET常用的等时间步长分支和等概率阈值分支两种分支规则进行DDET分支计算，其中等时间步长分支是指以特定时间步长等间隔分支，等概率阈值分支是指每个分支概率相同。本实例采用DG的恢复时间分布产生不同的事故情景，即在DDET分支规则中的分支概率由DG的恢复时间分布的累积分布给出，等时间步长分支和等概率阈值分支示意图如图5所示，计算中不考虑概率截断，终态规则是运行到任务时间结束。

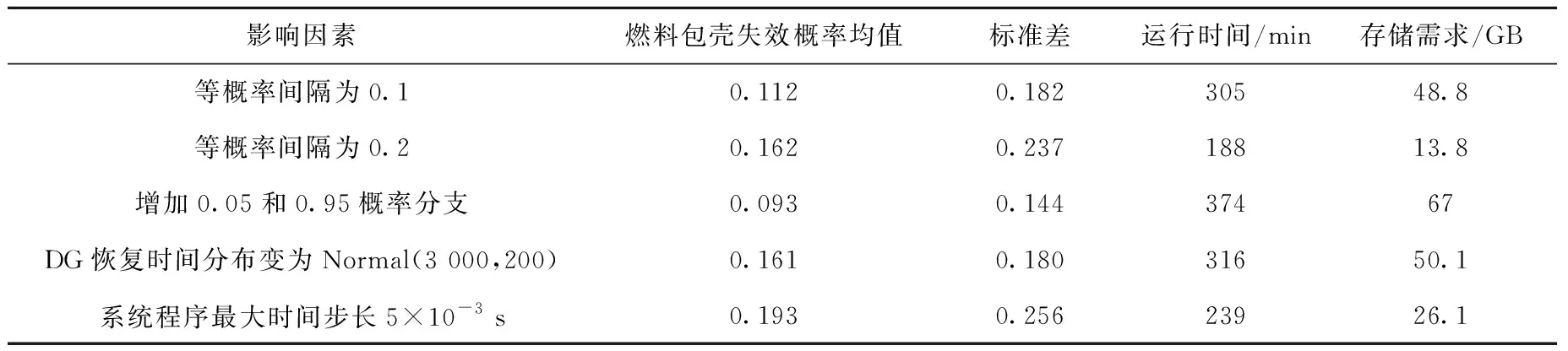
在等时间步长分支规则下，假设DDET等时间步长为100 s(图5a)，即DDET在DG恢复时间(单位为s)为[2 600.0，2 700.0，2 800.0，2 900.0，3 000.0，3 100.0，3 200.0，3 300.0，3 400.0]的时间节点分支，各分支节点对应的累积分布概率为[0.067，0.158，0.308，0.5，0.691，0.841，0.933，0.977，0.994]，则各分支的情景概率P(ti-1

a——等时间步长分支；b——等概率阈值分支图5 DDET常用的两种分支方法Fig.5 Two branch methods of DDET

图6 各情景下的燃料包壳温度Fig.6 Fuel cladding temperature under each scenario

3 影响因素分析

3.1 等时间步长分支规则

在等时间步长分支规则计算中考虑如下因素影响：1) 将DDET中DG恢复的等时间步长缩短至80 s，即DG恢复时间(单位为s)为[2 600，2 680，2 760，2 840，2 920，3 000，3 080，3 160，3 240，3 320，3 400，3 480]；2) 将DDET中DG恢复的等时间步长延长至150 s，即DG恢复时间(单位为s)为[2 600，2 750，2 900，3 050，3 200，3 350，3 500]；3) DG恢复时间分布变为Normal(3 000，200)；4) DDET根节点计算中的系统热工水力程序的最大时间步长修改为5×10-3s，各种不同因素下的燃料包壳失效概率均值列于表1。

表1 等时间步长分支规则下燃料包壳失效概率均值的影响因素分析Table 1 Analysis of factor affecting mean value of fuel cladding failure probability under equal time step branching rule

上述计算表明，DDET的分支时间步长越小，计算的分支越多，计算的燃料包壳失效概率均值越小，运行时间越长及存储需求越大。同时，关键参数分布和系统程序设置不同对燃料包壳失效概率均值有显著影响，因此也需要关注关键分布及系统程序参数设置的合理性。

3.2 等概率阈值分支规则

在等概率阈值分支规则计算中考虑如下因素影响：1) DDET等概率间隔置为0.2，即累积概率阈值为[0.2，0.4，0.6，0.8]；2) 增加累积概率为0.05和0.95的概率阈值，即DDET分支处的累积概率阈值为[0.05，0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，0.95]；3) DG恢复时间分布变为Normal(3 000，200)；4) DDET根节点计算中系统热工水力程序最大时间步长修改5×10-3s。各种不同因素下的燃料包壳失效概率均值列于表2。

表2 等概率阈值分支规则下燃料包壳失效概率均值的影响因素分析Table 2 Analysis of factor affecting mean value of fuel cladding failure probability under equal probability threshold branching rule

等概率阈值分支规则计算表明，DDET的等概率间隔越小，计算的分支越多，计算的燃料包壳失效概率均值越小，运行时间越长及存储需求越大。关键参数分布和系统程序设置的影响，与等时间分支规则下的计算结果类似，两者也对燃料包壳失效概率均值有显著影响。

3.3 改进的分支规则方法

可以看到，DDET的分支规则不同，燃料包壳失效概率均值的计算结果不同，分支越细致，计算结果越小，但需要的运行时间越长和存储空间越大。本文尝试寻找一种更好平衡风险指引的安全裕度计算中计算精度与计算资源匹配的分支规则方法。风险指引的安全裕度在数学上是计算负载分布与能力分布的重合概率，即负载上限分布对概率安全裕度的影响更大，负载下限对概率安全裕度的影响相对较小。本文提出一种可变的概率阈值分支方法，即在关键参数的DDET分支过程中，低概率累积分布区间的分支概率间隔相对大，高概率累积分布区间的分支概率间隔相对小。此外，本文特定问题下，若事故情景下计算的燃料包壳温度低于燃料包壳失效能力分布中的温度下限值，此情景下的燃料包壳失效概率为0，则在计算燃料包壳失效均值时，其对均值的贡献也是0。因此，可以采用DDET根节点(DG一直未恢复)燃料包壳温度信息和燃料包壳失效能力分布中的温度下限值确定温度下限值对应的DG恢复时间，再用DG恢复时间和DG恢复时间分布，计算此DG恢复时间下的累积概率。选择比此累积概率略小的概率作为DDET计算的概率阈值起点，这样可适当减少不必要的DDET分支计算及相应的计算资源。

可变的概率阈值分支方法下，设累积概率阈值为[0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，0.95，0.99]，概率阈值对应的DG恢复时间(单位为s)为[2 732，2 795，2 849，2 900，2 951，3 005，3 068，3 156，3 229，3 365]，计算得到平均燃料包壳失效概率及标准差分别为0.086和0.118，运行时间和存储需求分别为327 min和60.3 GB。若设累积概率阈值为[0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，0.95，0.99，0.999]，概率阈值对应的DG恢复时间(单位为s)为[2 732，2 795，2 849，2 900，2 951，3 005，3 068，3 156，3 229，3 365，3 518]，计算得到平均燃料包壳失效概率及标准差分别为0.085和0.116，运行时间和存储需求分别为350 min和72.4 GB。可以看到，恰当的分支规则可以提高计算效率，更好地平衡风险指引的安全裕度分析过程中的计算精度与计算资源的匹配问题。

4 结论与建议

本文研究了基于DDET的风险指引的安全裕度计算方法，针对简化压水堆模型下的SBO事故，利用Python程序计算了两种DDET分支规则下燃料包壳失效的风险指引的安全裕度及其不确定性，分析了分支规则、模型参数分布、系统热工水力程序内置参数设置对风险指引的安全裕度的影响。计算结果表明：1) 基于DDET的风险指引的安全裕度计算方法能够通过计算机编程自动大量的分支方法给出不同的事故情景后果和概率，进而定量统计给出特定问题的风险指引的安全裕度；2) 计算关键参数分布和系统程序设置不同对燃料包壳失效概率均值有显著影响；3) 分支规则不同，燃料包壳失效概率均值的计算结果不同，分支越细致，计算的燃料包壳失效概率均值越小，需要的运行时间越长和存储空间越大；4) 可变的概率阈值分支方法能够更好地平衡风险指引的安全裕度计算中的计算精度与计算资源的匹配问题。

随着计算机软硬件的快速发展以及先进算法的持续改进，核电安全分析中计算式的风险指引的安全裕度分析方法可能会更深入的实践，但在广泛应用此方法之前，需要更深入地研究此方法的不确定性评估、计算结果的验证以及能够有效提高计算效率的算法等问题，以更客观的辅助核电站在安全裕度方面的科学管理决策。