数控机床几何误差预测的GA-SVR模型

杨洪涛 , ，马群 , ，李莉 , ，张宇 , ，汪珺

（1. 安徽理工大学 机械工程学院，安徽淮南 232001；2. 安徽理工大学 矿山智能装备与技术安徽省重点实验室，安徽淮南 232001；3. 合肥学院 先进制造工程学院，合肥 230000）

数控机床在机测量系统常见是利用机床加测头方式组成，因此机床本身精度直接影响在机测量系统测量精度。数控机床几何误差主要包括定位误差、角度误差、直线度误差和垂直度误差，是影响机床加工精度和在机测量系统测量精度的重要因素[1]，但是由于垂直度误差在机床组装、出厂中已经存在，与速度和空间位置无明显关联且多为常数值，故不再进行误差比较。通过测量数控机床本体几何误差，并建立精确的几何误差模型，利用误差补偿方法，可以有效提高数控机床的加工精度和在机测量系统的测量精度[2-3]。数控机床每种几何误差均受到空间坐标位置、运动速度等因素影响，因此要实现数控机床几何误差的有效补偿，必须利用现代数学方法，建立高精度的多维误差预测模型。国内外学者对于各种几何误差建模预测方法分别开展研究[4-5]。王建平等采用了神经网络法对数控机床定位误差进行建模预测[6]。Fan等采用正交多项式回归方法对数控机床几何误差进行建模，将多项式回归问题转化为线性回归问题，以提高其建模精度[7-8]。冯文龙等使用了B样条曲线建模建立了直线度误差模型，提高了误差模型预测精度[9]。肖慧孝等使用了混合模型建模法对数控机床导轨直线度误差进行预测建模，并在这基础上进行了误差补偿[10]。杨洪涛等使用了粒子群优化支持向量机算法对数控机床的俯仰角和偏摆角进行预测建模[11]。周恒飞等使用支持向量回归机法对数控机床的定位误差、直线度误差、角度误差进行建模[12]。

上述研究成果多是采用不同方法研究单类误差高精度预测建模方法，存在建模方法通用性不足，建模精度有待提高等问题。由于不同机床几何误差产生原因不同，变化规律差异大。为了解决上述问题，本文通过搭建实验装置，分离机床几何测量误差，分析机床3种几何误差变化特点，针对几何误差数据特点和建模精度，利用遗传算法优化支持向量回归机（Genetic algorithm optimization support vector regression machin，GA-SVR）算法研究3种机床几何误差的精确建模方法，同时与其他3种建模方法进行比较。实现利用一种建模方法对不同几何误差统一建模，提高建模和误差预测精度。

1 数控机床几何误差变化特点

物体在三维空间中存在6个自由度，由于制造、安装误差的存在，数控机床移动副沿导轨运动时会产生6项误差，其中包括3项位置误差（1项定位误差、2项直线度误差），3项角度误差（偏摆角误差、俯仰角误差、滚转角误差），如图1所示。

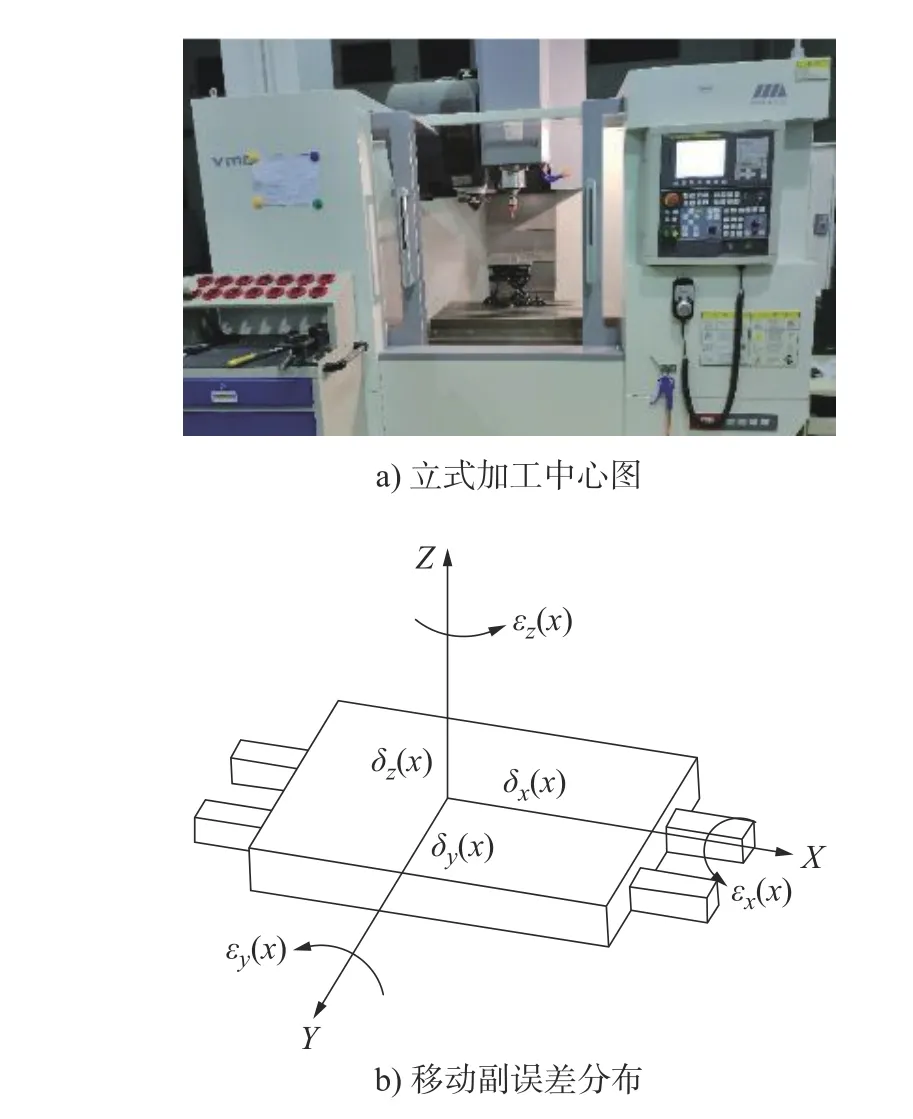
图1 X轴6项误差示意图

本文定义机床沿X轴运动时， δx(x)为其定位误差、 δy(x)为Y向的直线度误差、 δz(x)为Z向直线度误差、 εx(x) 为 沿X轴旋转的角度误差、 εy(x)为绕Y轴旋转的俯仰角误差、 εz(x)为绕Z轴旋转的偏摆角误差。数控机床沿Y、Z方向运动时的误差也按上述规则分别定义，加上三轴之间的垂直度误差εXY、 εXZ、εYZ，因此数控机床共有21项几何误差，如表1所示。

表1 加工中心21项几何误差

数控机床一个运动方向工作台由伺服驱动电机、联轴器、支撑轴承、滚珠丝杠、导轨、光栅系统和工作台台面构成。由伺服驱动电机通过联轴器，驱动滚珠丝杠旋转，带动丝杠螺母副和工作台台面做直线运动，通过光栅测量显示其运动位置。由于导轨存在制造和安装误差，电机驱动工作台施加的扭矩促使滚珠丝杠组件出现轴向变形，与滚珠丝杠的制造误差耦合在一起，引起滚珠丝杠存在螺距误差。同时在运动过程中机床会产生热误差，影响光栅测量系统的读数精度，这些因素使得机床工作台产生相应的定位误差、直线度误差以及角度误差，并且与机床的坐标位置有关。当XY工作台运动速度不同时，电机施加的扭矩不同，导轨副上产生的摩擦力也不同，同样会导致各项误差值的变化。因此，数控机床各单项几何误差受到机床坐标位置以及运动速度等多因素的影响。通过建立精确的几何误差模型，利用误差补偿方法，可以有效提高数控机床的加工精度和在机测量系统的测量精度。数控机床在机测量系统结构如图2所示。

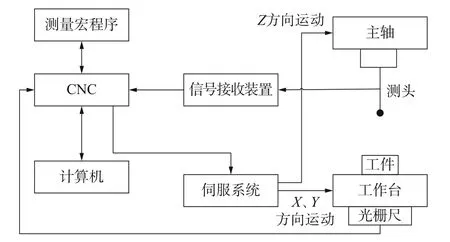
图2 在机测量系统结构图

2 GA-SVR算法

2.1 支持向量回归机（SVR）

使用支持向量回归机（SVR）进行数控机床几何误差的建模预测，其多用于小样本问题的回归预测，符合机床几何误差样本数少 的特点。数控机床几何误差预测建模，以机床运行速度和空间坐标位置作为自变量x， 误差值作为因变量f(x)建立回归函数，即

式中：x为机床空间坐标位置和运行速度构成的向量组，为在此速度和位置下的机床几何误差预测值； φ(x)为 非线性映射函数；w为权向量系数；b为 偏差量。

引入不敏感函数，数学语言表达为

式（2）中，当误差预测值f(x)和实测真值y之差ξi和，可将支持向量回归机的约束优化问题转化为：在范围内，则函数损失可以视为0。引入松弛变量

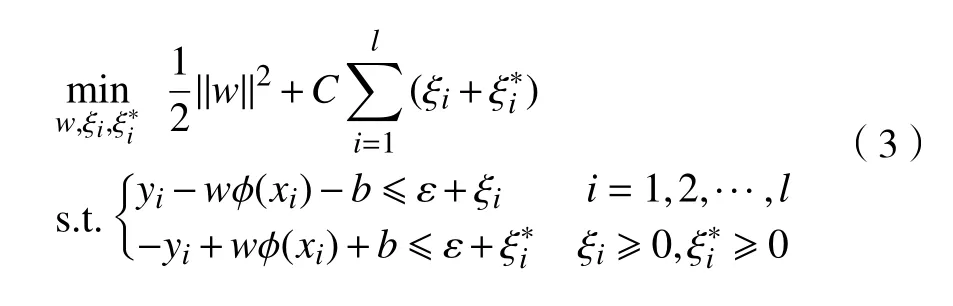
式中C为惩罚参数。引入Largrange函数，式（3）可转化为：

式中：K(xi,xj)为 SVR回归函数中的核函数，K(xi,xj)=为拉格朗日系数，。得到数控机床几何误差的预测数学模型[13-14]为

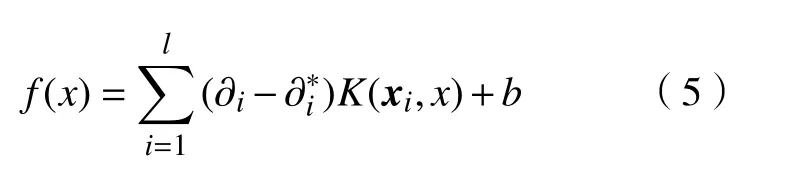
内部行政的有序性是现代企业生产运营的前提，同样也是企业在大数据环境和技术支持下对电子供应链金融风险管理的核心策略。通过实际调查发现，我国许多中小型企业对于企业内部电子供应链金融管理工作无法做出有效判断和行政管理。对此，首先需要完善内部风险行政管理体制，加强企业部门行政规划，保证部门工作的充分性和有序性，从而提高抵抗电子供应链金融风险的能力，给领导者提供有力的思想依据。此外，各行政部门的领导者需要及时转变自身观念，不要过分夸大或忽视金融风险的危害，推动企业行政规划更好更快发展。

高斯径向基核函数训练速度快，辨识效果佳，核函数参数更易选择，核函数的变动不会对空间复杂度产生太大影响[15]。根据机床几何误差数据特点，采用高斯径向基核函数用于几何误差建模，提高建模精度。

式中σ用来限制函数的径向作用范围，记1 /σ2为参数g。

2.2 遗传算法优化支持向量回归（GA-SVR）

遗传算法（GA算法）是一种常用的寻优进化方法，该算法的优化关键在于对参数的选择，将群体内目标问题的解编码为染色体，不断进行选择、交叉、变异以产生新的所需个体，得到符合求解目标的最优解。可以利用GA算法对SVR模型进行改进，不断搜索SVR模型的最优参数（核函数参数g和惩罚参数C），建立效果最佳的误差模型。优化算法步骤如下：

1）种群初始化：构建初始种群，将目标函数（核函数参数g和惩罚参数C）进行染色体编码。

2）计算适应度值：适应度值用来评价种群个体的优劣，方便对个体进行选择，误差预测值yi和误差实测真值Yi之间偏差的绝对值作为适应度值F。适应度函数为

3）选择操作：采用轮盘赌法从原有群体中随机选择个体i，进行种群重组操作。个体选择概率pi为

4）交叉操作：从原有种群中选择两个个体，进行交叉重组操作，新一代个体含有上一代个体的优良特征。染色体ak和ah在i位的交叉方式如下：

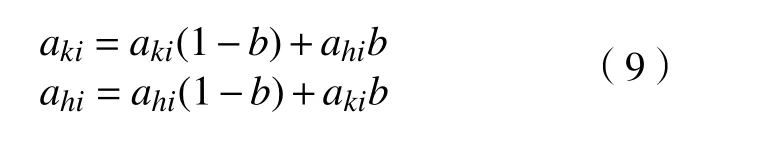
式中：amax、amin分别为选择基因的上下限；f(m) =r2(1-m/Gmax)2，m为当前迭代次数，r,r2为随机数，在[0,1]间选取，Gmax为最大迭代次数。算法迭代次数达到最大，停止操作，输出最优SVR模型参数，GASVR误差建模算法流程如图3所示。

图3 GA-SVR算法流程图

3 实验及建模结果分析

3.1 实验方案设计

数控机床在机测量系统常见是利用机床加测头方式组成，采用激光干涉仪测量机床几何误差，并建立相关精确模型，用于后续的数控机床在机测量系统误差补偿，可以有效地提高数控机床的加工精度和在机测量系统的测量精度。为了分析数控机床在不同坐标位置及运动速度等因素影响下的几何误差建模算法的优化效果，本文以VMC850E型立式加工中心为研究对象，展开相关实验。实验装置如图4所示，分光镜通过磁性座和安装组件固定于激光干涉仪前的三脚架上，反射镜固定在机床工作台上，反射镜随着机床工作台运行而产生移动。分别设置机床工作台运行速度v在1 ～ 20 mm/s范围内间隔2 mm/s取值，采用双频激光干涉仪对机床X、Y、Z轴运动行程为0 ～ 200 mm的定位误差、直线度误差和角运动误差进行测量。每隔5 mm采集一次误差数据，重复测量3次取平均值作为最终误差测量结果。将各误差数据分别代入4种误差建模方法进行训练及预测建模，比较其建模预测精度。

图4 实验测量现场图

分别采用BP神经网络算法、GA-BP算法、SVR算法和GA-SVR算法分别对机床各单项误差进行预测，数控机床测量的三项线值误差数据（μm）和角度误差数据（"），各算法相关参数设置如下：

BP神经网络算法网络参数设置：训练次数2000次，学习速率0.1，训练目标为0.001。

GA-BP算法迭代参数设置：种群规模为80，最大遗传代数为20，交叉概率为0.8，变异概率为0.05；训练次数2000次，学习速率0.1，训练目标为0.001。该神经网络包含三层网络结构，以X轴坐标位置（Y或Z轴坐标位置）、运动速度2个变量作为输入节点，机床单项误差1个变量作为输出节点，隐含层含有5个节点。

SVR采取网格法划分网格，在[0，50]区间内以一定的步长搜索最佳的惩罚参数C和核函数参数g。

GA-SVR算法参数设置：种群规模为80，最大遗传代数为20，交叉概率为0.8，变异概率为0.05。C、g参数搜索范围区间为[0，50]。

3.2 4种算法预测建模对比分析

为了更好比较不同空间位置和运动速度下4种算法对同一类误差的建模预测效果，本文以机床X轴5项单项误差建模为例，分别采用4种算法建立误差模型与对比。

将机床的运动速度v= 10 mm/s，机床行程在0 ～ 200 mm内的不同位置下41个样本误差数据和X= 100 mm，机床运动速度v为1、3、5、8、10、12、14、16、18、20 mm/s的不同速度下10个样本分别作为建模效果测试数据，其余空间坐标位置和运动速度下的误差数据分别作为训练数据。利用4种算法建模，并分别预测运动速度为v= 10 mm/s和空间位置X= 100 mm的X轴几何误差数据，与实测的误差数据比较建模精度。不同位置和运动速度下4种算法的建模精度比较结果如图5和图6所示，误差建模均方误差和模型预测值与实测真值之间最大残差值如表2和表3所示。

表2 不同位置下4种算法建模比较

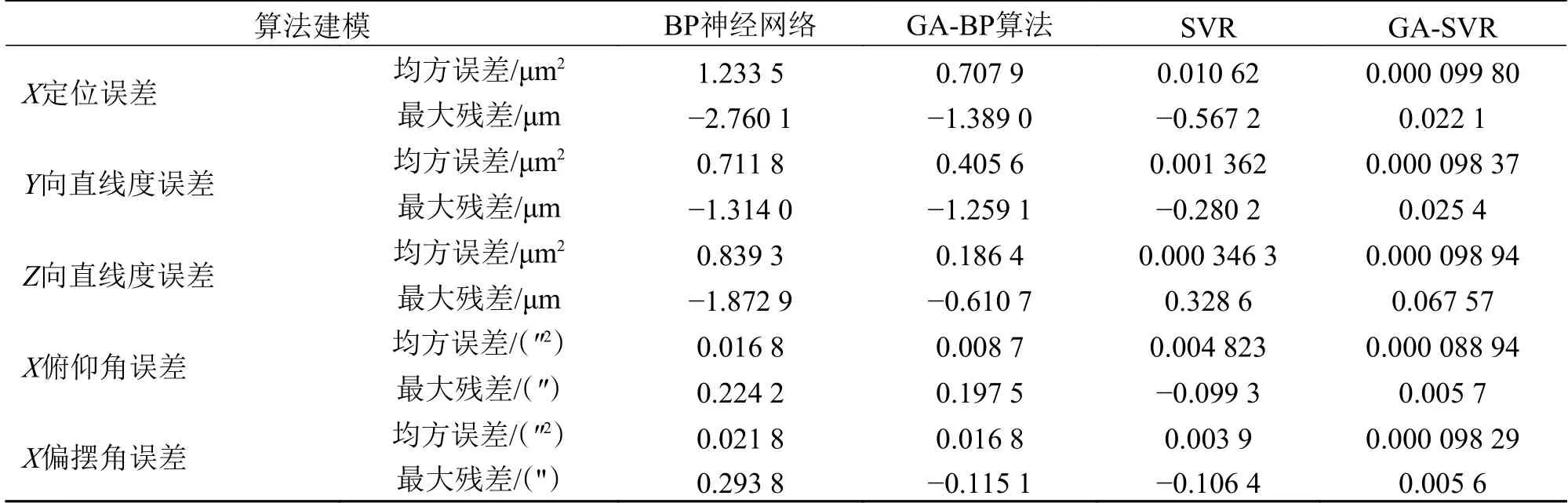
表3 不同速度下4种算法建模比较

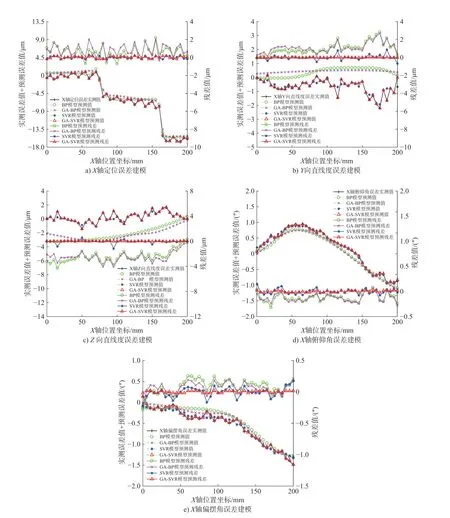
图5 不同位置下X轴单项误差建模对比

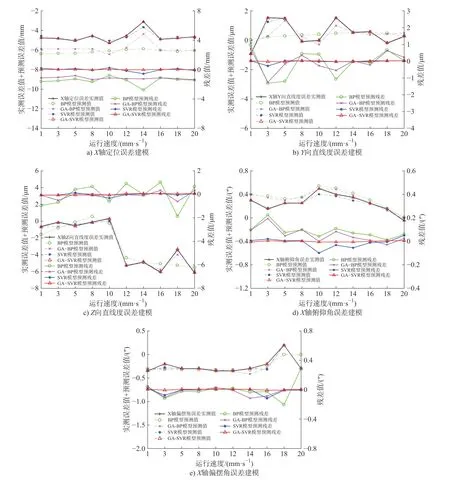
图6 不同速度下X轴单项误差建模对比

由图5、图6、表2和表3可知，以机床X轴3种几何误差为例，无论是处于不同空间位置坐标下，还是改变机床的运动速度，4种算法对于机床几何误差建模预测精度关系：GA-SVR ＞ SVR ＞ GA-BP神经网络 ＞ BP神经网络。1）BP神经网络算法对3种机床几何误差建模精度低，残差分布波动大，均方误差值最大；2）GA-BP神经网络算法对直线度、定位误差建模预测精度较低，残差分布波动明显，均方误差较大。3）SVR算法对定位误差建模精度稍高，模型预测值和实测值偏差稍大，预测均方误差稍大，不适用于定位、直线度误差建模；4）GA-SVR对于定位、直线度误差和角度误差建模预测精度最高，3种几何误差模型预测值与实际测量值偏差接近于0，位置误差建模最大残差值为0.1796 μm，角度误差建模的最大残差为0.0192"，建模预测均方误差值最大为9.98×10-5μm2。3种误差统一建模效果明显优于其他3种算法。

同理，分别利用4种算法对机床Y、Z轴几何误差建模。不同空间位置或者运动速度下，相较其他3种算法，GA-SVR算法建模精度最高，误差预测值和实测值偏差最小，均方误差相对最小且处于同一量级。不同空间位置处，GA-SVR算法对机床Y、Z轴几何误差建模，其中Z轴定位误差残差值最大为0.2591 μm，不同速度下，该算法Y轴Z向直线度误差建模残差值最大为0.04291 μm。验证了GA-SVR算法对3种机床几何误差统一建模精度高，效果最好。

4 结论

1）对影响数控机床几何误差的各单项误差变化特点进行了分析，推导出数控机床的空间位置以及机床运动速度等是影响机床定位误差、直线度误差以及角度误差的主要因素。

2）根据机床误差特点，提出一种基于遗传算法优化的支持向量回归机几何误差建模预测算法（GA-SVR），利用GA算法优化选择SVR参数（惩罚参数C、核函数参数g），达到最优的建模效果。

3）利用激光干涉仪搭建实验装置分离不同运动速度和空间位置的机床几何误差，分别利用4种不同算法对测量出的机床X轴运动时的定位误差、直线度误差、角运动误差进行建模比较，结果证明GA-SVR算法对3种机床几何误差的预测建模精度最高，均方误差最小；定位、直线度误差两种位置误差建模的最大残差分别为0.1796 μm、0.06757 μm，角运动误差建模的最大残差为0.0192"，可以用于数控机床3类几何误差的精确建模。