IRS与人工噪声辅助的MIMO通信系统物理层安全方案设计

景小荣，宋振远，罗 悦，马玉丹

（1.重庆邮电大学通信与信息工程学院，重庆 400065；2.移动通信技术重庆市重点实验室，重庆 400065）

0 引 言

利用超材料制造的智能反射表面（intelligent reflecting surface，IRS），无需昂贵的射频单元和复杂的基带处理电路，就可实现对无线电磁环境的智能操控，进而使系统容量和能量效率均得到明显提升，因此IRS有望在未来移动通信中得到广泛应用。

近几年，基于IRS辅助的无线通信技术引起了国内外学者的广泛关注。在针对IRS辅助的无线通信的研究中，除少部分研究工作着眼于系统性能的理论分析外，大部分研究主要集中在基于IRS辅助通信系统的波束赋形、功率分配和信道估计等关键技术方面。在众多关键技术研究方面，文献［5］针对IRS辅助的多输入单输出（multiple input single output，MISO）系统，以最大化用户接收信号总功率为目标，研究了基站（base station，BS）波束赋形矢量和IRS相移矩阵的联合优化设计；文献［6］则以最大化多播组和速率为目标，研究了IRS辅助的下行多组多播MISO系统预编码矩阵和IRS相移矩阵设计。Wu等人分析了离散相移IRS的功率增益，并指出当IRS单元规模比较大时，离散相移可取得与连续相移相同的功率增益。文献［8］针对IRS辅助的多蜂窝无线网络，以最大化小区边缘用户最小可达速率为目标，研究了基于多点协作的联合处理中的BS预编码矩阵和IRS相移系数设计。Wei等人提出了一种双结构-正交匹配追踪算法来实现IRS辅助通信系统的信道估计。为了最大化MISO系统的能量效率，文献［10］利用梯度下降法优化相移矩阵，利用丁克尔巴赫算法优化功率因子。文献［11］研究了在统计信道状态信息下多输入多输出（multiple input multiple output，MIMO）系统的波束赋形方案。文献［12］研究了5G中的信道模型对IRS和译码转发中继性能的影响，并得出IRS和译码转发中继之间可达到性能互补的效果。文献［13］在考虑了IRS相位噪声和BS量化误差的条件下，毫米波通信系统的上行可达速率表达式，并得出系统的性能在IRS数量不限时仅受基站端模拟数字转换器（analog digital converter，ADC）分辨率的影响。文献［14］研究了使用快速增强学习的方法来对抗IRS辅助的通信系统中多天线干扰器对通信系统的干扰。文献［15］分析了IRS辅助的移动边缘计算中时延最小化问题，并利用块坐标下降的方法将问题分解成子问题迭代求解。文献［16］利用博弈论的方法研究了IRS辅助的动态网络服务选择的问题。

由于IRS技术的应用依赖于无线电波的传输特性；而无线电波在开放的自由空间传输使得无线信息易被窃取。庆幸的是，无线物理层安全利用无线信道的内生安全机制，为安全通信提供了一种可行解决思路。因此，在IRS辅助的无线通信系统中，利用IRS能够智能构造无线传播环境这一特征，可增强无线通信系统的安全性。近年，Cui等人利用交替迭代和半定松弛（semidefinite relaxaton，SDR）算法，通过优化IRS相移矩阵设计，显著地提高了系统的保密速率。考虑到SDR算法的复杂度相对较高，文献［19］提出利用最小化最大化（minimization maximization，M M）算法和二分搜索算法来设计IRS相移矩阵。针对IRS辅助通信系统中存在多个窃听者和合法用户场景，文献［20］基于深度强化学习，研究系统物理层安全方案设计。文献［21］研究了IRS辅助的毫米波MISO通信系统的鲁棒性和安全波束赋形设计。文献［22］研究了IRS辅助的具有安全性能的认知无线通信系统，并考虑3种窃听者的信道状态信息（channel state information，CSI），即窃听者CSI完全已知、部分已知和完全未知。

在典型物理层安全方案设计中，还可通过在发送信号中混入人工噪声来提升物理层安全。文献［23］针对MISO系统仅存在单个无源窃听者时，通过合理设计波束赋形矢量和人工噪声矢量来提升系统安全性能。在BS仅知窃听者信道的统计信道状态信息时，Wang等人针对单蜂窝MIMO系统，给定安全区域的条件下，通过最大化安全概率，提出一种人工噪声辅助的安全传输策略。文献［25］针对大规模MIMO中继系统，在无法获得窃听者信道状态信息的情况下，采用最大比合并／最大比发射信号处理方案，并配合中继零空间人工噪声和目的端的协作干扰来实现多用户信息的安全传输。上述研究仅借助人工噪声来实现通信系统的物理层安全设计，随着IRS技术的普及，有必要融合IRS与人工噪声，来开展无线通信系统物理层安全的研究。

在上述分析的基础上，本文针对IRS与人工噪声辅助的MIMO通信系统，提出一种基于迭代算法的物理层安全设计方案。在该方案中，首先根据均方误差准则对系统保密速率函数作等价转化，然后利用交替优化的思想，先固定IRS相移矩阵，利用凸优化方法优化BS端波束赋形矩阵和人工噪声协方差矩阵；接着固定这个两个变量，利用基于黎曼流形的共轭梯度下降算法优化IRS相移矩阵；交替迭代过程直至安全速率函数收敛为止。仿真结果表明，本文提出的IRS和人工噪声辅助的物理层安全设计方案具有良好的系统保密速率性能。

1 系统模型

考虑如图1所示MIMO下行通信系统安全模型。在该系统中，以BS作为发送端，接收端包括一合法接收者和一窃听者；同时IRS模块包含个反射单元。假设BS配置天线N ≥2根天线，合法接收者和窃听者分别配置天线根数N 和N ，且N ＞2，N ＞2。同时，假设BS与合法接收者以及窃听者之间的链路被建筑物完全阻隔，只有BS到IRS链路以及IRS到合法接收者链路、IRS到窃听者链路。为提高物理层安全性能，BS在发送信号中混入人工噪声矢量，则BS发送信号可表示为

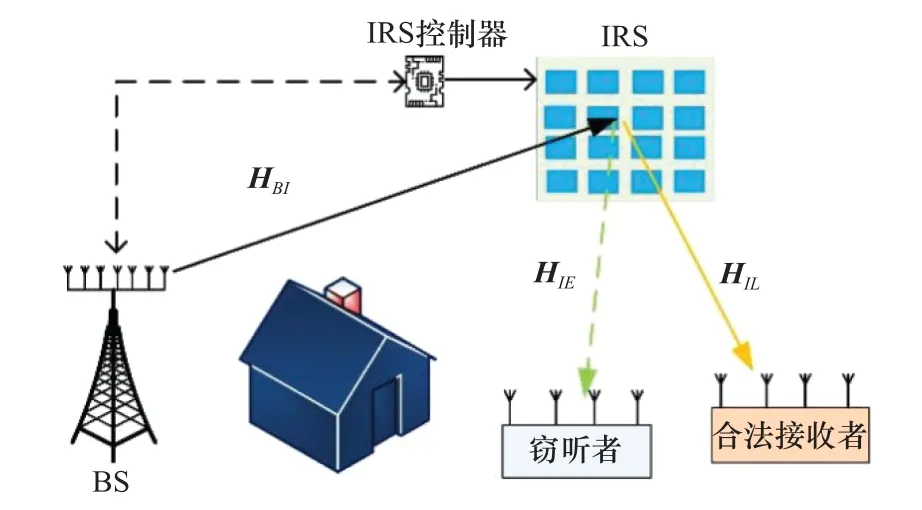
图1 MIMO下行通信系统安全模型Fig.1 Security model for MIMO downlink communication system

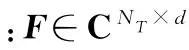
根据上述系统配置，同时考虑准静态平坦衰落信道模型，则合法接收者处的接收信号可表示为

2 问题提出

假设BS确知全部信道状态信息，并能够通过BS-IRS之间的无线链路给IRS控制器发送相应的相位调整信息，IRS根据控制器根据该信息对入射信号的相位调整后，然后进行反射。于是，在合法接收者处的信息接收速率为

根据式（7），基于系统保密速率最大化准则，构建如下优化问题：

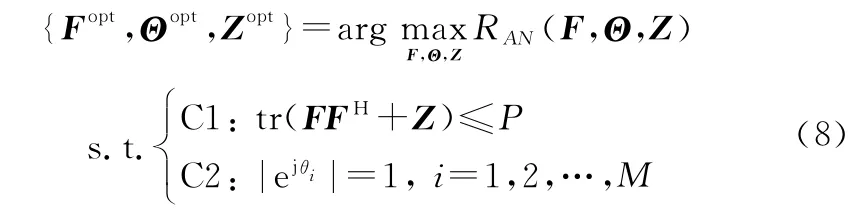
其中，约束条件C1表示对BS发送功率的限制，约束条件C2表示对IRS相移矩阵中相移系数的约束。显然，式（8）为一非凸优化问题，其求解需联合优化设计BS波束赋形矩阵、人工噪声协方差矩阵，以及IRS相移矩阵。式（8）作为非凸问题，直接求解十分困难。

给定变量、和V 初始值后，辅助变量组的值可通过式（14）、式（15）、式（18）、式（20）和式（21）求得，然后这些辅助变量代入式（22），将式（22）进一步化简为

3 IRS与人工噪声辅助的物理层安全方案设计

由式（24）～式（28）以及H ＝H ΘH 和H ＝H ΘH 可知，IRS相移矩阵与波束赋形矩阵以及人工噪声协方差分解矩阵V 耦合在一起，而且式（24）中约束条件C2为非凸约束项，因而无法直接获得式（24）的最优解；但是变量与V 之间无耦合关系，因此可采用交替迭代来对其优化求解，即先固定IRS相移矩阵，求解变量束｛，V ｝；进而固定变量束｛，V ｝，求解IRS相移矩阵；交替迭代直至目标函数收敛，即可获得目标函数的次优解。下面给出更为详细的分析过程。

3.1 波束赋形矩阵以及协方差矩阵优化设计

固定IRS相移矩阵时，式（24）中约束项仅包含发送功率的约束，于是，将式（25）和式（26）代入式（24），则有

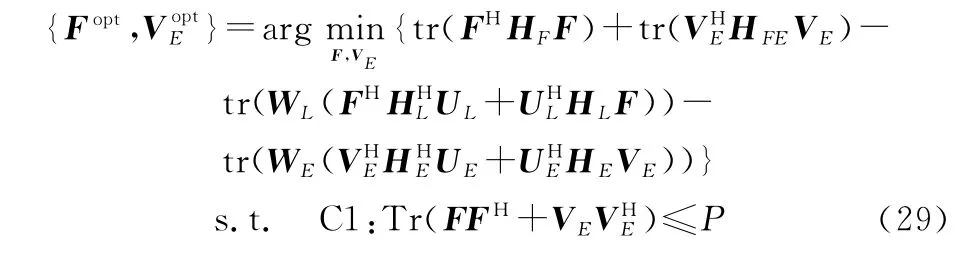
观察式（29）可知，该优化问题为标准的凸优化问题，因此可采用凸优化中的内点法求解。在凸优化工具箱中，文中采用mosek solver求解优化问题式（29）。

3.2 IRS相移矩阵优化设计

根据上述分析，由第3.1节确定波束赋形矩阵以及协方差矩阵V 后，固定和V ，来求解IRS相移矩阵。固定变量束｛，V ｝时，式（24）中约束项仅包含IRS相移矩阵中相移系数的约束，于是，式（24）可表示为

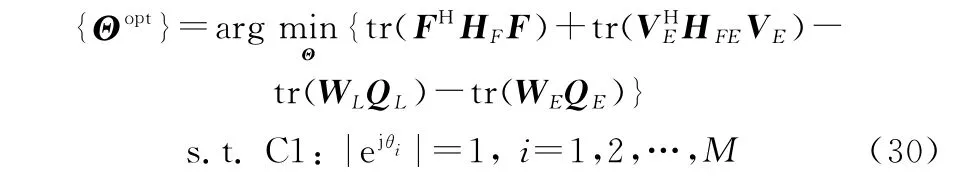
为便于问题求解，首先将式（30）中目标函数进一步写作：

观察式（42）可知，该问题为一带非凸约束的非凸优化问题。如果采用常规的SDR算法来求解，将会导致比较高的复杂度，为此文献［26］采用优化最小化的方法求解式（42），但该方法涉及特征值分解，复杂度也相对较高。因此，本文采用基于黎曼流形的共轭梯度下降算法，可在解决非凸约束项的同时，进一步降低优化式（42）的复杂度。

在上述分析基础上，下面给出上述利用基于黎曼流形的共轭梯度下降算法求解式（42）中的具体过程。

3.3 基于交替迭代的参数优化设计

根据交替迭代的思想，首先给定变量束｛，V ｝、的初始值，代入式（14）、式（15）、式（18）、式（19）和式（21），利用目标函数为凹这一性质确定辅助变量U 、W 、U 、W 和的优化值；然后固定IRS相移矩阵，将已确定的辅助变量U 、W 、U 、W 和代入式（29），接着利用CVX建模系统中mosek solver求解式（29），以获得变量束｛，V ｝的优化值，进而将｛，V ｝代入式（42），利用基于黎曼流形的共轭梯度下降算法求解式（42），以确定，即可确定IRS相移矩阵的优化值。上述过程交替迭代进行，直至系统保密速率达到收敛。下面给出了基于交替迭代的参数优化设计过程。

4 复杂度分析

5 仿真分析

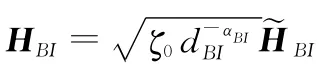
图2 仿真中各个参量的坐标表示Fig.2 Coordinate representation of parameters in simulation

为了验证本文方案的有效性，将下列方案与本文方案进行了对比。

文献［26］中提出的基于块梯度下降（block coordinate descent，BCD）和MM 算法的方案 该方案首先基于BCD思想，结合拉格朗日乘子法来计算及V ，最后使用MM算法获得相移矩阵。

无人工噪声的方案 令V ＝0，用内点法来求解，的求解方法与文献［23］中相同。

随机相位选取方案 采用内点法来确定和V ，则由［0，2π］产生的随机数确定。

图3给出在IRS反射单元数＝128时系统保密速率随功率的变化情况。根据图3，文中提出的方案显然优于3种对比方案。当较低时，为保证有效通信，BS大部分发送功率配置给，导致文中所提方案与BCD-MM方案性能及无人工噪声的方案性能相近；随的增大，BS发送功率不但可保证需要，还存在充足的剩余功率来设计人工噪声矢量，此时，导致文中设计方案性能明显优于无人工噪声的方案。同时，由于随机相移选取方案没有设计相移矩阵，因此其保密速率较低，从而说明IRS相移参数对于系统性能的重要性。

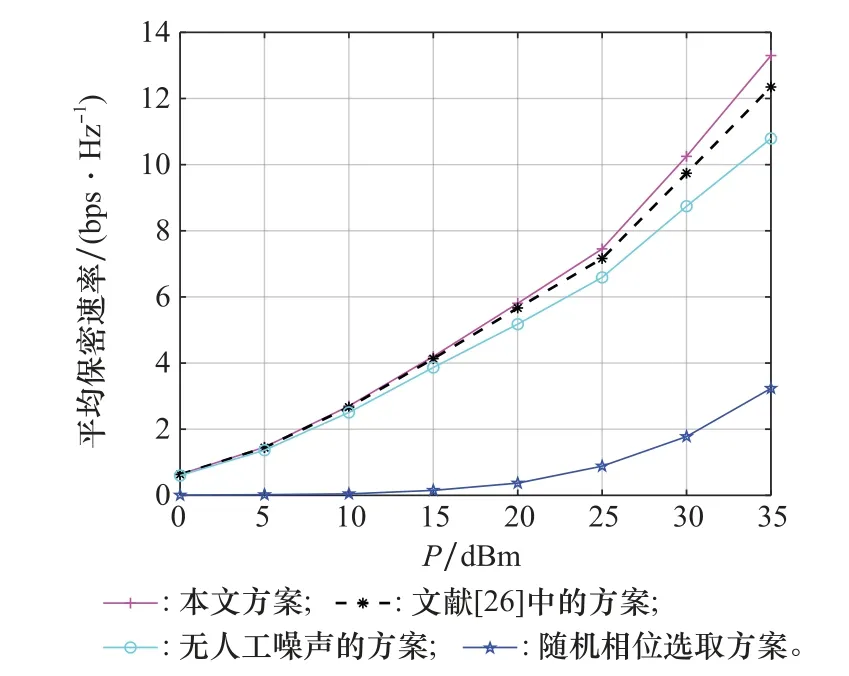
图3 M＝128时系统保密速率随功率P变化情况Fig.3 Change of system security rate with the power P when M＝128

在＝30 d Bm条件下，图4给出系统保密速率性能随IRS单元数的变化情况。显然，随IRS单元增加，因IRS提供的辅助增益的提升，使信号更容易到达合法接收者，同时窃听者接收到BS发送的干扰信号将更强，导致合法接收者接收信噪比与窃听者的接收信噪比比值增大，进而使得保密速率性能得到提升。同时，对于无人工噪声设计方案，由于其无法对窃听者实现干扰，导致保密速率必然比本文方案低；对于随机相位方案，因IRS单元数的增加并未给其带来信道增益的提升，所以其性能提升非常缓慢。

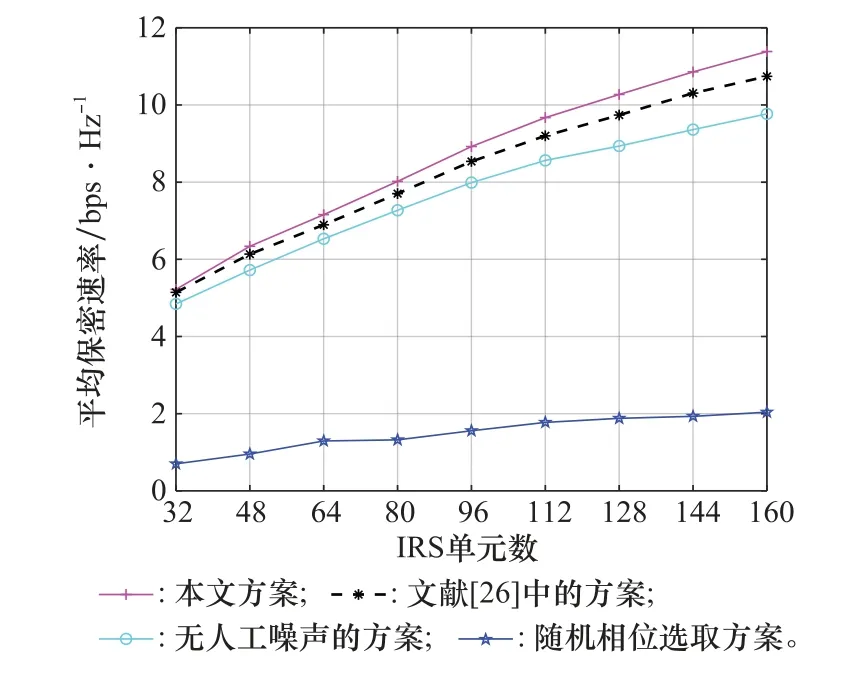
图4 IRS单元数对系统保密速率的影响Fig.4 Effect of the number of IRS units on the system security rate

设定＝128，图5给出系统保密速率性能随合法接收者位置变化的结果。仿真中，令合法接收者在坐标（40 m，0 m）与（120 m，0 m）之间移动。从该仿真可看出：随合法接收者向IRS逐渐靠近，保密速率性能逐渐得到提升，且在二者相距最近时，性能达到峰值；随二者相距增大，系统保密速率性能则逐渐降低。这是因为当合法用户和IRS单元相距较近时，合法用户方可接收到更多的有用信号能量，从而说明：在IRS辅助通信系统中，IRS单元的合理放置对系统的影响非常大。

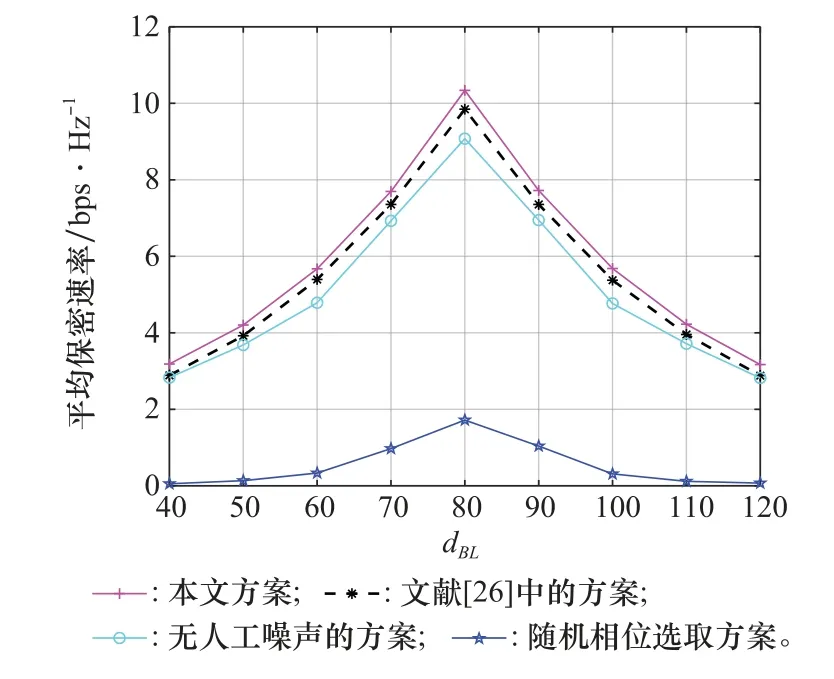
图5 M＝128时合法接收者移动对系统保密速率的影响Fig.5 Effect of the movement of legitimate receivers on the system security rate when M＝128

图6给出IRS单元数＝128和BS发送功率＝30 dBm时，当与IRS相关的链路损耗指数均相等时，即α＝α＝α＝，路径损耗指数变化对系统保密速率的影响。

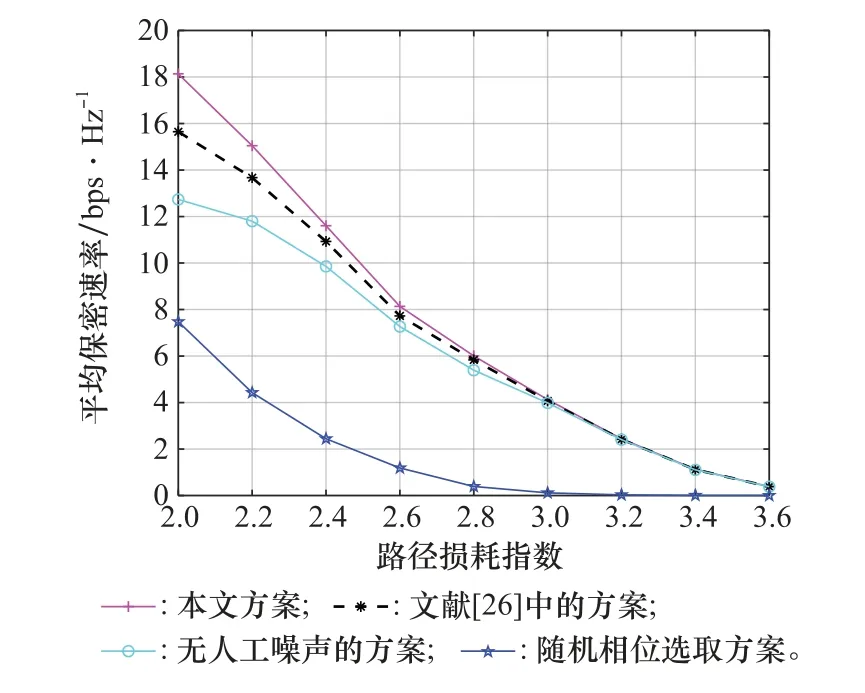
图6 M＝128和P＝30 d Bm时路径损耗指数变化对系统保密速率的影响Fig.6 Effect of path loss exponent change on the system security rate when M＝128 and P＝30 dBm

根据图6，对于路径损耗相对较小时，由于信号的传输衰减也小，从而导致系统保密速率性能较优；但随其逐渐增大，系统保密速率性能逐渐降低。特别当＝3时，基于BCD-MM的方案及无人工噪声设计的方案与本文所提方案性能相似。这进一步说明：为了规避障碍物的阻挡，IRS的部署位置必须合理安排。

6 结 论

本文研究了IRS与人工噪声辅助的MIMO通信系统中的物理层安全设计方案。文中假设确知完美信道状态信息，在该条件下，通过优化设计波束赋形矩阵、IRS反射相移矩阵及人工噪声协方差矩阵来实现系统保密和速率性能提升。为了实现该目标，文中构建一非凸优化问题。然而由于该问题是一多变量耦合问题，直接求解十分困难。为此，引入均方误差准则，通过引入一系列的辅助变量，对非凸优化问题进行预处理，从而将原始问题变为一易于求解的问题；进而利用内点法来实现波束赋形矩阵以及人工噪声协方差矩阵的求解。同时，IRS相移矩阵则结合基于黎曼流形的共轭梯度下降法使之得以求解。与对比方案相比较，文中所提出的物理层安全设计方案具备更为优良的性能。