利用蒙特卡罗模拟评估空气间隙对点扫描质子治疗的剂量影响

陈蕾，余行，傅玉川，韩纪锋

1.四川大学华西医院放疗科，四川成都 610041；2.四川大学原子核科学技术研究所/辐射物理及技术教育部重点实验室，四川成都 610064

前言

由于质子独特的深度剂量特性可以显著地降低靶区近端与远端正常组织的剂量，降低辐射毒性，相比传统光子治疗更有优势，使得质子放疗得到了广泛的关注与应用［1-2］。从技术层面来看，笔形束扫描（Pencil Beam Scanning,PBS）是目前主要的质子治疗实现方式［2］，具体又可分为点扫描和光栅扫描两种模式。

当治疗靶区位于体内相对深的位置时，质子治疗计划系统（TPS）能够保证足够的计算精确度［3-4］。但当靶区靠近浅表位置时，需要采用射程移位器（Range Shifter, RS）降低射束能量，从而实现患者体表治疗［5］。RS 不能过于靠近患者放置，以避免其与治疗中的患者发生碰撞而引发安全事故［6］，因而在RS 末端和病人体表之间存在一段空气间隙（Air Gap,AG）。对于点扫描模式，AG 的存在会改变束斑的尺寸，不同射束能量和AG 会得到不同的束斑尺寸［7-8］。随着束斑尺寸增加，可能会改变需要照射层面的束斑间隔，从而影响靶区内的剂量分布［9］。在实际临床工作中，需要将AG 对靶区的剂量影响考虑在内，尤其是在倾斜射束、AG 较大、介质非均匀的治疗条件下［10］。为了系统地评估使用RS 时AG 对质子输运计算结果的影响，本研究在通用蒙特卡罗（Monte Carlo, MC）程序Geant4［11］平台上建立了点扫描质子束流模型，模拟计算各种条件下AG 的存在对水模体内剂量分布的影响。

1 材料与方法

1.1 MC模拟设置

采用通用MC 软件Geant4 v10.7.2，物理列表选择QSGP_EBRT_EMV，最大步长设置为0.1 mm，每种情况模拟跟踪106个粒子。运用MC 进行剂量计算需要知道射束的各种参数，包括能量（E）、能量展宽（ΔE）、束斑大小（σR）、束斑角分布（σθ）。Paganetti等［12］发现将MC运用到临床质子治疗剂量模拟时，上述参数中最关键的参数为能量展宽，因为它会影响布拉格峰的宽度、远端衰减的斜率和峰坪比。为便于模型的验证，本文中的ΔE设置与其一致，如式（1）所示：

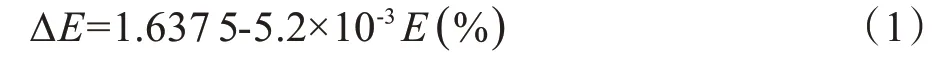
图1 显示模拟计算的几何模型。模拟背景为空气，紧贴治疗头（nozzle）出口放置RS，RS 材料为水，厚度设置为其水等效厚度（Water Equivalent Thickness,WET），RS后端间隔一段距离放置水模体，尺寸为40 cm×40 cm×40 cm，以20 cm×20 cm×0.1 cm的网格收集水模体中的剂量，间隔距离可以改变以提供不同的RS 与水模体之间AG。质子束流从治疗头出口向右发射，分别模拟不同能量（110、150、190 MeV）、不同束斑大小（4.0、6.5、8.0 mm）、不同束斑数目（1、121、289、束斑间隔1σR）的结果，以及2 种RS 规格［RS40（WET=4.0 cm），RS75（WET=7.5 cm）］的结果。研究上述参数条件下4 种AG 长度（0、10、30、50 cm）对水模体中的剂量分布的影响。

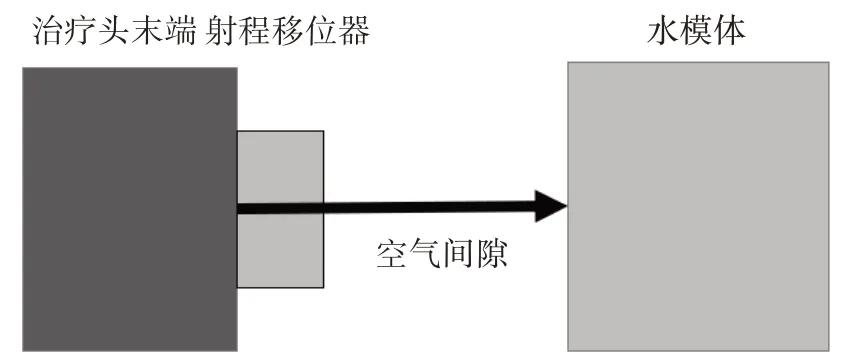
图1 不同AG时质子放疗的MC模型Figure 1 MC model of proton radiotherapy with different air gaps(AG)

1.2 模拟数据验证

为了验证本文模拟方法是否正确，将使用RS40，σR=6.5 mm的110、150、190 MeV质子在AG 0 cm时水模体中的剂量沉积数据进行归一化，获得积分深度剂量（Integrated Depth Dose, IDD）分布曲线，并与Paganetti 等［13］在相同条件下获得的实验数据进行对比。结果发现两者可较好地符合，表明模拟程序准确可靠，详细对比结果见2.1部分。

1.3 剂量差异分析方法

Zhang 等［14］提出剂量修正因子G(z,a) ，对低于临床要求的计划使用G(z,a) 进行剂量修正，剂量验证的伽马通过率均得到了提升。G(z,a) 表示与AG（acm）相关的剂量损失率，可由等式（2）计算获得：

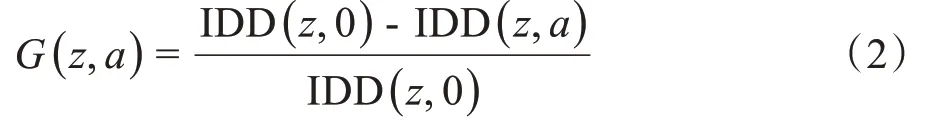
其中，IDD(z,0 )表示AG 0 cm、深度zcm 时的积分深度剂量，IDD(z,a)表示同条件同深度下AG为acm时的积分深度剂量。通过G(z,a)与标准剂量IDD(z,a)可得到AG 为acm、深度为zcm 时的准确剂量IDD(z,a)，修正过程如等式（3）所示：

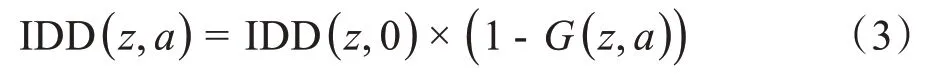
本文基于模拟获得的IDD曲线，利用等式（2）生成G(z,a)用于评估AG对剂量带来的影响。若G(z,a)越大，则表明AG对该深度时的剂量影响越大。

2 结果与分析

2.1 MC模型的验证结果

图2 中从左到右的实线分别表示AG 0 cm、RS40、σR=6.5 mm 时110、150、190 MeV 的单束质子流在水模沿中心轴的剂量沉积归一化IDD 曲线，空心圆为Paganetti 等［13］在相同条件下实验测量得到的数据。对比两者可以发现模拟值与测量值有很好的一致性，证明本文中的模拟方法和模型是正确的。

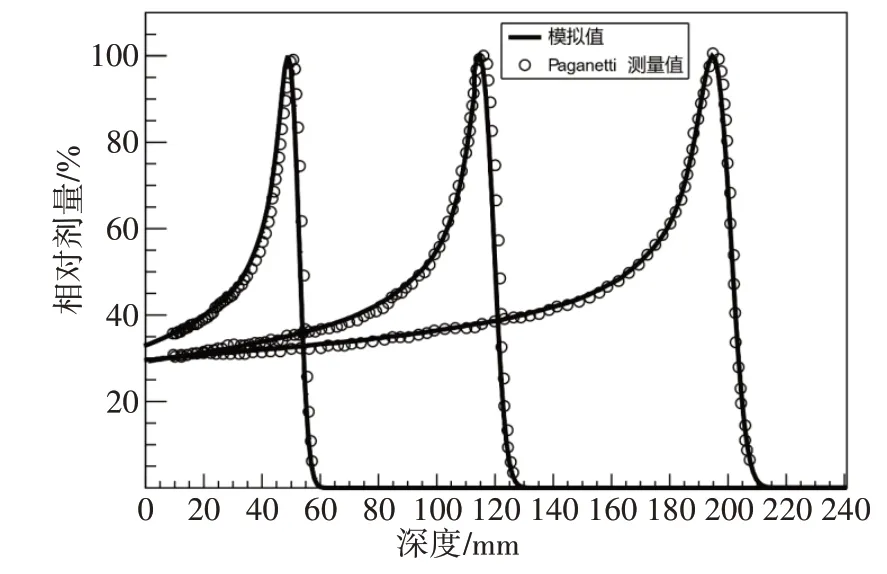
图2 本文模拟的IDD曲线与Paganetti等的测量值比较Figure 2 Comparison between IDD curves simulated in the study and the measured values of Paganetti et al

2.2 不同束流能量时AG对剂量的影响

图3 显示模拟使用RS40 时150 MeV 的单能质子在4 种AG 长度下的IDD 曲线模拟结果，可以看到随着AG 的增加，IDD 曲线前端的剂量降低，且越靠近浅表其下降越明显。基于模拟得到的IDD 曲线利用式（2）计算得到使用RS40 时110、150、190 MeV 质子在AG 为10、30、50 cm 时的G(z,a) ，并生成对应能量布拉格峰深度前的G(z,a) 深度图，如图4 所示。图4a～图4c分别显示不同AG时不同能量质子的G(z,a)深度图，可以看到G(z,a)均随深度的增加而减小。在同一能量下，G(z,a)随AG 的增加而增大。图4d显示不同质子能量在AG 50 cm 时的G(z,a)深度图，图中显示当AG 恒定时，G(z,a)随能量的增加而增大，且非0 区域随能量的增加而变深。在模拟条件下，最大的G(z,a)出现在质子能量最高（190 MeV）、AG 最深（50 cm）、最靠近体表（深度0 cm）时，对应的G(z,a)值为0.106。

图3 不同AG时150 MeV质子的IDD曲线Figure 3 IDD curves of 150 MeV proton with different AG

当射束通过RS 时，会发生横向散射而变宽［15］，从而增大束斑的尺寸和横向半影［7,16-17］，束斑的尺寸可通过AG 与束流能量的3 次多项式拟合得到［8］。Kelleter 等［18］发现随着质子能量的增加，次级电子对质子剂量建成的贡献逐渐增加；当能量恒定时，随着AG 的增加，次级电子的贡献逐渐减小。Winterhalter等［19］发现AG 增加，束斑在水中的横向半影会增加，但随着深度的增加，横向半影逐渐减小。

因此，AG 的增大可能会导致更多次级粒子在AG 中损失而无法到达水模体，从而造成剂量损失。当束流能量越大时，次级电子的损失更大，剂量损失也就越大，但随着深度的增加，差异逐渐减小。

2.3 不同RS时AG对剂量的影响

图5显示150 MeV 质子在不同RS 时的IDD 曲线与G(z,a)深度图。从图5a 中可以看到不同的RS 会改变IDD 曲线，RS的WET 值增厚会导致布拉格峰位置向体表移动。对比图5b 和图4b 可以发现，由于RS40 的布拉格峰值更远离体表，因此剂量需要修正的深度也越深。当AG 较小时，RS40 的G(z,a)相比RS75 更大；AG 较大时，较浅时RS75 的G(z,a)更大，但随着深度的增加，RS40的G(z,a)更大。

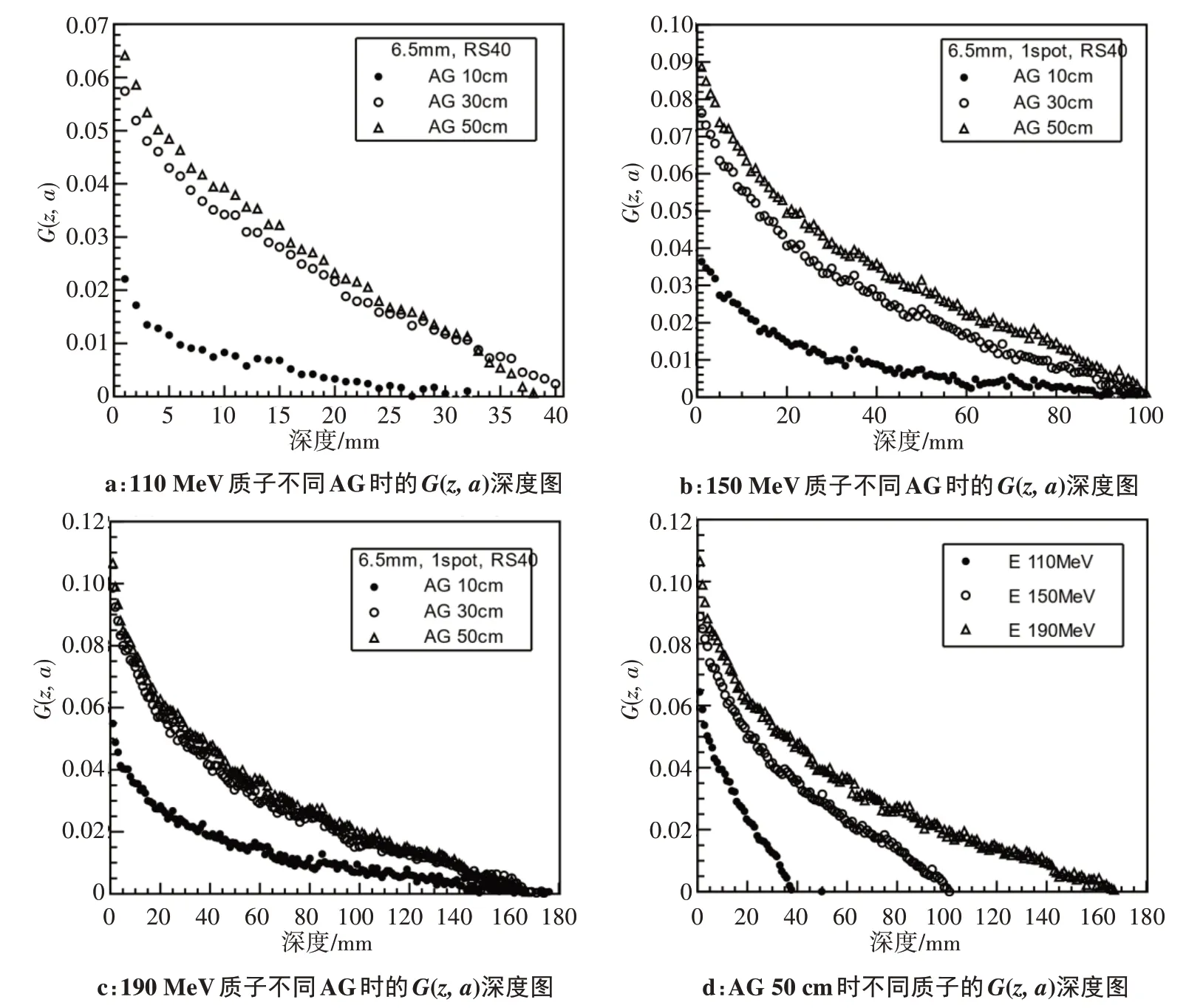
图4 不同条件时G(z,a)深度图Figure 4 G(z,a)-depth profiles in different conditions

图5 150 MeV质子在不同RS时的IDD曲线与G(z,a)深度图Figure 5 IDD curves and G(z,a)-depth profiles of 150 MeV protons with different RS

Shen 等［20］研究指出RS 的WET 变薄，散射长度越小，束斑尺寸越大，剂量损失增加。Rana 等［8］对比了RS40 与RS75 不同AG 时的束斑大小，发现在能量相同时，RS75 与RS40 束斑尺寸的比值随着AG 的增加逐渐增大。Maes 等［21］发现可通过AG 与深度的二次多项式拟合得到横向半影尺寸，AG 较小时，RS75的横向半影更小，随着AG 的增加，RS75 的横向半影会逐渐大于RS40；随着深度的增加，RS75 的横向半影衰减速率高于RS40。

因此，在AG较小时，WET较小的RS的束斑尺寸和横向半影更大，对剂量的影响更大；随着AG增大，RS的WET越厚，束斑尺寸和横向半影越大，对剂量的影响越大，但随着深度的增加，其横向半影衰减更快，使得对剂量的影响逐渐小于WET更薄的RS。

2.4 不同束斑大小与束斑数目时AG对剂量的影响

图6显示使用RS40的150 MeV质子在AG 10 cm与50 cm 时不同束斑大小和不同束斑数目时的G(z,a)深度图，可以发现与同能量单束流时的G(z,a)差异并不大。

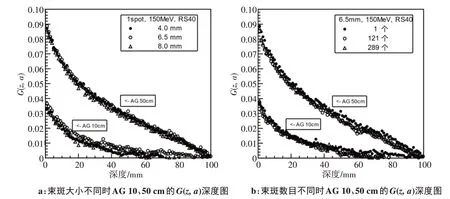
图6 使用RS40的150 MeV质子在AG 10、50 cm时不同束斑大小和不同束斑数目时的G(z,a)深度图Figure 6 G(z,a)-depth profiles of 150 MeV protons with RS40,different spot sizes and beam numbers at AG of 10 and 50 cm

Paganetti等［13］通过改变束斑尺寸和角分布，发现对剂量的影响并不明显，仅改变能量展宽对同能量束流存在明显影响。Trnkova 等［22］发现剂量的差异依赖于肿瘤的深度和大小、束斑的数目、AG、核相互作用修正因子，在肿瘤位置较浅和束斑数目少于103时会出现较大的剂量差异。Van De Water 等［23］通过反复调整减少调强质子治疗计划中权重较小的扫描点（从33 855 个减少到1 510 个），可以在不影响计划质量和交付准确性的情况下缩短治疗交付的时间。

由于本文模拟的能量展宽依据式（1）设置，未做其他改变，仅改变了束斑的尺寸；模拟的束斑数目较少且设置简单，与实际的临床计划有较大差异。因此，束斑的大小和较少的束斑数目对剂量的影响与同能量时单束流质子对剂量的影响无显著差异。

3 讨论

本文通过Geant4 建立点扫描模式下使用RS 时治疗头末端的质子束流模型，模拟计算了在不同能量、不同RS、不同束斑大小、不同束斑数目在不同AG条件下的水模体中剂量沉积，并参照以往研究中提出的G(z,a)进行分析，评估了AG对剂量的影响。结果显示在使用RS 时造成的AG 会使得剂量下降，尤其是靠近浅表部分，能量越高剂量差异越大，RS 的WET较薄时，差异更明显。

目前用于临床的TPS 多采用解析剂量算法（Analytical Dose Calculation, ADC）。Shirey 等［24］发现在使用RS 的情况下，TPS 的剂量准确性会受到深度、AG 和RS WET 的影响。Tommasino 等［25］发现采用ADC 算法时，较大的AG 会导致乳腺癌计划质量下降。Widesott 等［26］发现在使用RS 时或使用较大AG 时，对于头部肿瘤计划，ADC 会高估靶区的剂量和低估危及器官的剂量。Rana 等［27］对比不同AG 时10 例乳腺癌调强质子放疗的肿瘤控制率，发现随着AG 增加，肿瘤控制率均下降。较大的AG 会导致计划质量的下降，甚至更差的预后；但较小的AG 也会导致患者与设备太靠近而造成安全隐患，甚至提升皮肤剂量［28］。

在实际的临床工作中需要选择合适的AG。在保证患者安全情况下，若使用RS且不做其他处理，选择较小的AG 可以保证较深处肿瘤计划的准确性，达到临床要求。但当肿瘤位置较浅、AG 较大时，可以在测量加速器常用束流能量的剂量沉积数据基础上，结合相同条件下MC模拟得到的数据建立G(z,a)数据库应用于TPS系统来对剂量进行修正。

本文也存在一些不足：（1）模型构建较为简单，只模拟了束流从治疗头出射的部分，未考虑束流在加速器内的情况；并且RS 使用了WET 的水模体代替，未模拟具体材料，与实际的加速器有一定差距；（2）本文模拟的数据较少，只模拟了特定束流使用特定RS 在特定AG 时的情形，普遍情况下的影响还需要更多的模拟；（3）本研究主要是在文献基础上进行模拟和分析讨论，对于AG 在临床上的实际影响，仍需进一步验证和研究。