测量误差、偏差、精度和准确度的正确剖析
2022-10-09王江山刘汉青段艳君张志芳
■王江山 刘汉青 段艳君 张志芳
多年来在实际操作中,计量人员对涉及的测量误差、测量准确度、测量仪器的准确度等概念上存在模糊认识。当前在一些技术标准中,经常需要对测量仪器的准确性进行定量规定,有用准确度表示,也有用精度来表示。尤其是关于精度一词,长期以来颇受争议,本文针对测量误差、偏差、精度和准确度等进行正确分析。
1 误差和偏差
在实际工作中,凡提到误差,都有一定的对象。如零件的制造误差、量具的误差、测量误差、读数误差和温度误差等。概括地说,误差就是实际数值与真实值的差。所谓真实值,严格地讲,是无法测得的,这是因为测量仪器、测量方法、环境、人的观察力等都不能做到完美无缺的缘故,在实用中,只能用尽可能接近它的值来代替。误差的对象不同,真实值的代用值也不同,如在制造零件时,取零件的公称值;检定量具时,取标准量具(如量块)所确定的值;测量时,取多次测量结果的算术平均值多为真实值。
误差按其性质分为三大类:
(1)系统误差:是大小与方向不变,或按一定规律变化的误差。它是由于量具的误差、标准件误差、读数误差、测力误差以及温度误差等引起的误差。量具的误差主要包括量具零件的制造偏差、量具装配误差和设计上不合理或采用了某些假定引起的误差。系统误差一般可通过一定的方法加以修正或消除。
(2)偶然误差:是一种大小和方向都不定的误差,又称随机误差。量具本身引起的偶然误差是由于量具零件的磨损、量具机构有时间和摩擦、测力的变化,以及油层带来的停滞现象等原因引起的。偶然误差是不可避免的,不可能一一掌握,但是在进行多次测量时,用统计的方法,也可以找出它的变化规律和变动范围。其变化规律是:正负偶然误差出现的次数相等;绝对值相等,符号相反的偶然误差出现的次数相等;绝对值小的偶然误差比绝对值大的偶然误差出现的可能性大,并且偶然误差的绝对值不会超过一定的极限。
(3)过失误差:是由于测量和计算时的疏忽和错误造成的粗大误差。如读错、记错、听错、算错、量块组合错、偶然的碰撞、震动、温度的改变、工件安装错等原因造成的误差。
量具检定中,常常碰到偏差这一概念。偏差又有极限偏差和实际偏差之分。极限偏差是规定的;实际偏差是实际得的。例如尺寸为25mm 的千分尺校对杆,其尺寸极限偏差规定为±2μm,如果校对杆尺寸超差,可按实际测得的尺寸使用。这个实际尺寸与公称尺寸25mm之差,就是实际偏差。偏差和误差有时没有明显的区别,在数值上也往往是相同的。误差和偏差均有正负之分。
2 精度和准确度的区别
精度和准确度是两个含义不同的基本概念,为了说明这两个概念及它们之间的关系,我们举一个打靶的例子。有三位民兵在同样的外界条件下,并排向三个靶子各射击若干发子弹。射击结果如图1 所示。由图可以看出,第一位民兵发射的子弹射击点最集中(图1a),散布范围最小;第二位散布范围较大(图1b)。我们就可以说,第一位的射击精度比第二位高。第三位的射击点也很集中(图1c),但是离靶心很远。我们说,第三位与第一位的射击精度相近,但第三位比第一位的射击准确度低。
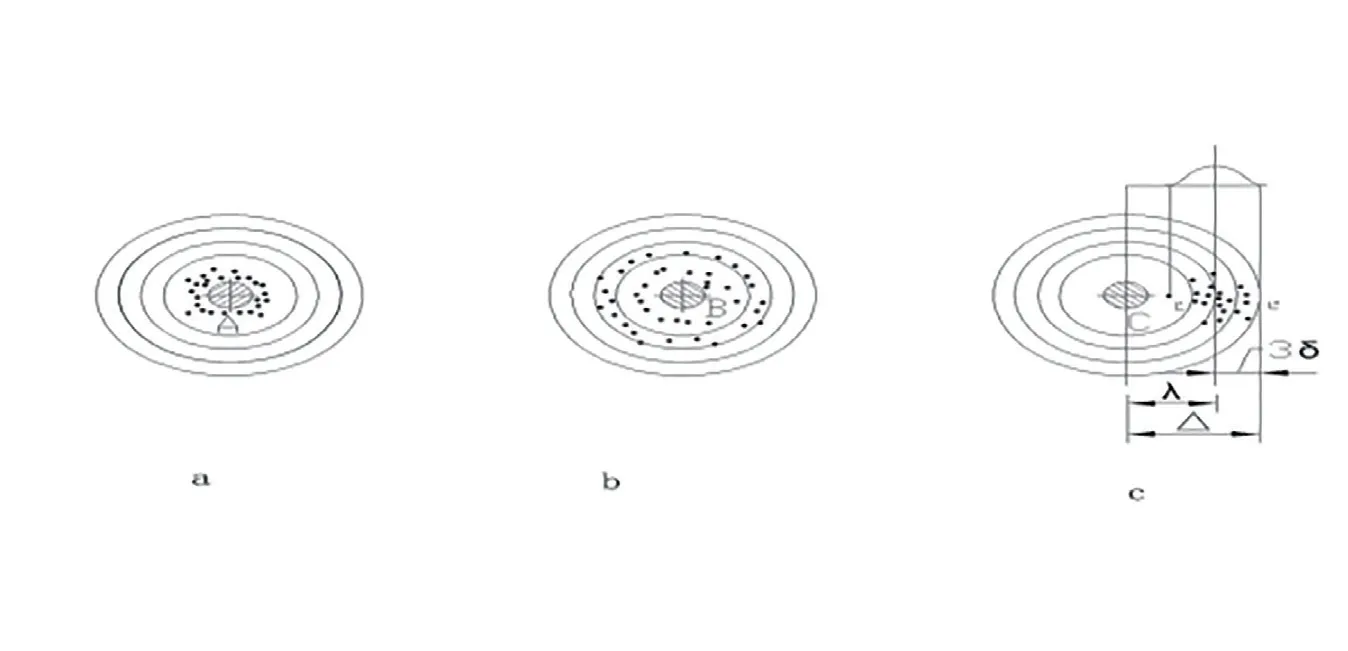
图1 以打靶为例说明精度和准确度的概念
就打靶来说,精度就是各子弹射击点相接近的程度;准确度就是射击点与靶心接近的程度。
由此可知,只有多次射击才谈得上精度,它是对一批数值说的。精度反应了误差的散布范围。因此,它不是用误差大小表示,而是用误差的散布范围大小来表示。下面用一个例子来说明:有两个同类量具,精度分别为0 级和1 级,用0 级量具测得的数值中,可能有些值比用1 级量具测得的某些值误差更大。如果简单地用误差大小来表示精度,那就会得出0 级精度比1 级精度低的矛盾结论来。若用每个量具的误差散布范围表示精度,就比较合理了。这就好比图1a 中,有某些射击点(如A 点)比图1b 中某些点(如B 点)距离靶心较远,但不能说前一种情况的射击精度比第二种低。
3 精度、准确度和误差的关系
为了说明精度和准确度与误差的关系,以及怎样用数量来表示它们,就要用到偶然误差和系统误差这两个名词。我们仍然用打靶为例,精度的高低(射击点的散布范围大小)是由于偶然的因素决定的,如射击者呼吸不均匀、手发生颤动等。准确度的高低(射击者偏离靶心的距离)是由于固定的因素和偶然的因素决定的,如枪的准星校正不好、射击者的眼睛有问题,以及上述的偶然因素等。所以,精度与偶然误差有关,而准确度既与偶然误差有关,也与系统误差有关。它们在数量上的关系可用图2 表示。
图2 中曲线为偶然误差的分布曲线,横轴表示射击点对靶心的误差,纵轴表示误差相同的射击次数;O 相对于靶心(误差为0);λ 为射击结果含有的系统误差;L′和L′′表示射击点离靶心最近和最远的误差;L′和L′′之间的距离表示射击结果不确定度的程度,即精度,也就是偶然误差的极限,数值上等于6(在误差理论中,称为标准误差或均方根误差,它是一组测量中各个观测值的函数,用来表示精度。)Δ 称为最大可能误差,表示精确度,数值上等于。如果将图2 与图1c 进行比较,就更加清楚了。
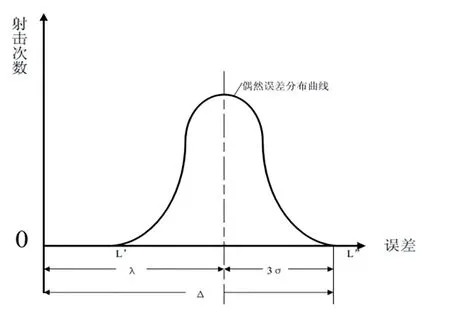
图2 精度和准确度数量上的关系
由可知,一个精度很高的射击结果,可能是不准确的(系统误差可能很大),正如图1c 所示的情况;也可能是准确的(可能很小,甚至为0),正如图1a所示的情况。反过来讲,如果准确度高(当即表示准确度),则精度(也高,所以,准确度才能全面地衡量射击成绩的好坏)。
