基于LSTM的一次风机在线监测及故障诊断研究

2022-10-08王远鑫

安徽电气工程职业技术学院学报 2022年3期

王远鑫

(中国大唐集团科学技术研究总院有限公司华东电力试验研究院, 安徽合肥 230011)

0 引言

随着火力发电机组辅机趋向大型化，辅机设备的安全运行直接影响到火电厂的安全生产[1]。辅机设备发生故障不但会影响正常的电力生产，甚至会造成重大人身伤亡事故。因此对辅机设备状态进行实时监测对于火电厂安全生产具有重大意义。

根据历史数据建立能反映设备状态参数的预测模型，已成为国内外学者对设备状态监测的主要方法之一。Tapan[2]模仿人类专家的判断行为，对工厂的复杂状态工作进行评估。文献[3]基于多变量分析的参数劣化分析对风机的振动进行回归。文献[4]基于能量平衡和质量平衡建立磨煤机动态数学模型对磨入口一次风温、磨电流、磨出口温度进行回归并验证。

近年来，最小二乘支持向量机因其具有小样本、非线性、预测精度高等特点越来越多用于建立电站设备状态参数预测模型。文献[5]提出了一种基于最小二乘支持向量机(LS-SVM)模型状态估计的一次风机在线仿真分析。文献[6]通过运行数据对振动值进行回归建模，对比了LS-SVM与BP神经网络回归误差，LS-SVM均方根误差(RMSE)小于BP神经网络。文献[7]基于LS-SVM建立具有较高的建模精度的一次风机状态估计的预警模型。

辅机设备状态参数受同一时间点系统其它状态参数影响，且参数在时间域上具有前后关联性，因此以往仅考虑状态参数在空间域上的关联性不符合设备参数演变的实际规律。应从时间和空间双重域上提取参数特征[8]。文献[9]提出了基于LSTM的交流电机系统故障诊断方法，具有较高的故障辨识准确率。循环神经网络(RNN)模型虽然考虑了样本时间域的关联性，但记忆能力有限，难以提取长期数据的特征。长短时间记忆网络(LSTM)，在RNN基础上，引入记忆细胞单元，可学习样本长期的时序依赖性。

本文采集的电站一次风机正常运行数据与x方向轴瓦振动异常时数据，预处理后分为训练、测试集进行LS-SVM、LSTM回归训练，在测试集对比两种模型均方根误差(RMSE)，证实了LSTM在一次风机参数回归方面较LS-SVM具有更高回归精度。对异常状态x方向轴瓦振动、y方向轴瓦振动、自由端轴承温度进行LSTM回归训练，计算三类参数正常状态自适应阈值，对比异常时数据与自适应阈值关系，进行一次风机故障诊断。

1 算法模型

1.1 LS-SVM模型

支持向量机(Support Vector Machines，简称SVM)是一种二分类模型，它的目的是寻找一个超平面来对样本进行分割，分割的原则是间隔最大化，最终转化为一个凸二次规划问题来求解。如图1所示，SVM实现的即为包含一个多隐含层的感知器。

图1 支持向量机示意图

SVM估计模型的目标是寻找到一个最优函数f(x)拟合训练样本，首先考虑线性回归函数，对于给定的训练数据，回归的目标是回归误差尽可能小，为此，引入ε不敏感损失函数，所有训练样本均在精度下ε无误差拟合:

{(xi,yi)|i=1,2,…,n}

(1)

|yi-(wTxi+b)|≤ε

(2)

(3)

|yi-(wTxi+b)|≤ε

(4)

s.t.-(ε+ξi)≤yi-wTxi-b

(5)

(6)

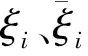
(7)

(8)

将原问题转化为对偶问题：

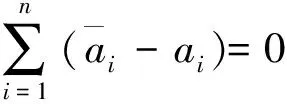
(9)

回归函数为：

(10)

1.2 LSTM模型

LSTM模型基础结构图如图2所示，a和b表示输入和输出单元。M是记忆单元，通过与自身的循环连接，获得记忆能力。图中神经元包括输入门(Input Gate)、输出门(Output Gate)和遗忘门(Forget Gate)。

图2 LSTM模型示意图

门控制单元接受四个输入，分别是当前时刻的输入变量x(t)、前一时刻Block的输出以及邻接Block的输出h(t-1)、前一时刻cell的状态s(t-1)及自身的偏置向量bk(k=f,o,i)。每一部分对应的输入输出如下。

Input Gate:

(11)

Forget Gate:

(12)

Output Gate:

(13)

(14)

记忆单元M的输入分别来自输入门的输出和当前时刻的输入部分乘积及遗忘门的输出与上一时刻对应的Cell状态的乘积；输出门的输出与记忆的单元的输出相乘作为整个Block的输出。对应关系如下。

Cell:

(15)

(16)

Block Output:

(17)

1.3 自适应阈值

超过预警阈值即设备发生故障，但阈值的选取标准会影响判断结果。现有的故障预警研究往往选取某一一般正常状态偏差的最大值或相似度最低值作为预警阈值。但在实际中，经历不同变工况阶段辅机的运行状态会不同程度偏离正常状态。与此同时，现场测量、传输过程的干扰也会引起相似度下降，因此采用原有阈值预警会造成误报。

由切比雪夫不等式推导可知，对于任意具有有限均值和有限方差的随机变量，其取值范围为[μ-zδ,μ+zδ]，其中μ和δ分别为随机变量的均值和方差。因此在辅机正常运行时，可推出在N个时刻下ε的取值区间C为[εN-zδN,εN+zδN]，其中εN为N个时刻的均值，δN为N个时刻的方差。具体表达式为:

(18)

(19)

由式(18)、(19)可看出，计算N时刻的误差均值只需用到N时刻的误差和N-1时刻的误差均值；计算N时刻的方差只需用N时刻的误差，N-1时刻的方差和N-1时刻的误差均值。

文中一次风机数据采集自M电厂2号机组B一次风机，该一次风机采用双级动叶调节轴流风机，型号为AP2-17/12，锅炉最大出力(BMCR)工况设计煤种进口体积流量104.4 m3/s，风机全压14 700 Pa，调节方式为液压动叶调节，叶片调整范围为-30°～20°。电机型号为YKK630- 4，类型为鼠笼式异步电动机。

2B一次风机DCS采集的测点包括：一次风机电流、一次风机出口压力1、一次风机出口压力2、一次风机出口压力3、一次风机动叶执行机构位置、一次风机轴承温度、一次风机风机端x方向轴瓦振动、一次风机风机端y方向轴瓦振动、负荷。各测点位置如图3所示。

图3 一次风机测点示意图

2 数据预处理与分析

由于电站数据库的历史数据存在坏点、噪声等影响，无法保证参数的准确性。如果存在错误参数，会对后面的计算模型造成误差。与此同时，部分电站测量设备因工作环境恶劣极易出现故障及失真问题，因此在对数据进行计算前必须对参数进行预处理。

2.1 状态判别

状态判别是根据逻辑判断采集数据当前状态。若设备状态为GOOD，则保持原值不变；如果状态点为BAD，则赋予其一特定值，特定值的选取为该点5 min内的平均值。

2.2 插值处理

因设备类型存在不同，各设备采集数据长度参差不齐，为建立完整、统一的数据集，需对数据进行差值处理，进而得到同样时间点的完整数据。对数据处理过程中，以5 s为插值的间距，采用直线插值法，将数据补充完整。

2.3 数据滤波

因采集到原始数据经插值处理后存在干扰与噪声，需采用滤波对数据中干扰与噪声滤除。考虑到历史数据为连续时间段平稳数据集，采用中值滤波更能还原数据的真实性。

中值滤波是基于排序统计理论的一种能有效抑制噪声的非线性信号处理技术，其基本原理是把数字序列中一点的值用该点的一个邻域中各点值的中值代替，从而消除孤立的噪声点。

2.4 数据分析

为分析各参数间关系，计算各参数标准相关系数(Standard Correlation Coefficient，也被称作皮尔逊相关系数)。

相关系数衡量随机变量X与Y相关程度的一种方法，相关系数的取值范围是[-1,1]。相关系数的绝对值越大，则表明X与Y相关度越高。当X与Y线性相关时，相关系数取值为1(正线性相关)或-1(负线性相关)。

皮尔逊相关系数计算公式如下式所示:

(20)

各参数皮尔逊相关系数见表1所示。

表1 相关性较大的各参数系数表

由表1可知，与y方向轴瓦振动相关参数相关性由大到小依次为：出口温度>自由端轴承温度>轴承温度>电流>动叶机构执行位置>x方向轴瓦振动；与自由端轴承温度相关性大小由大到小依次为：轴承温度>出口温度>y方向轴瓦振动>电流>动叶机构执行位置>x方向轴瓦振动>负荷；与x方向轴瓦振动相关的参数较少且相关性较弱，相关性大小由大到小依次为：y方向轴瓦振动>自由端轴承温度>轴承温度>出口温度>负荷。

因一次风机故障为x方向轴瓦振动测点异常，为使回归参数能充分体现故障，选用自由端轴承温度、x方向轴瓦振动、y方向轴瓦振动作为回归参数。

对一次风机的总样本数据划分训练集与测试集，且训练集与测试集的比例大小为4∶1。

采集数据均为一次风机油箱油位正常时数据，故认为油箱油位对一次风机轴承温度、自由端轴承温度无明显影响。y方向轴瓦振动与多项预测参数呈现强相关性，因此首先对y方向轴瓦振动参数进行回归预测，选用输入参数为：出口温度、电流、动叶执行机构位置；其次对自由端轴承温度进行回归预测，选用输入参数为：出口温度、回归的y方向轴瓦振动、电流、动叶执行机构位置、负荷；最终对x反向轴瓦振动进行回归预测，选用输入参数为：回归的y方向轴瓦振动、回归的自由端轴承温度、出口温度、负荷。

为防止输入参数因各参数量纲不同，造成回归时训练速度缓慢甚至无法收敛，对输入参数进行标准化处理，公式如下所示。

(21)

3 结果分析

3.1 LSTM与LS-SVM回归结果对比

以5 s为时间间隔，共采集1 739条数据，其中正常运行状态750条，故障状态989条。将数据集按4∶1进行划分，其中训练集数量为1 393条，测试集数量为346条。

3.1.1y方向轴瓦振动回归结果

在调整参数后，选用最大迭代次数(epochs)=50训练步长(batch_size)=20，隐含层神经元为9，Adam作为训练优化算法，双隐含层的LSTM进行回归训练，测试集回归值与原始值对比如图4所示。

图4为测试集数据y方向轴瓦振动预测回归值与实际值对比，由图像可看出无论正常状态或故障状态，预测回归值变化趋势与实际值变化趋势均相同，且两者偏差较小。为综合评价LSTM预测回归准确性，引入均方根误差RMSE计算公式对预测回归值进行计算，其大小为0.020 mm。

图4 LSTM模型y方向轴瓦振动测试集回归值

LS-SVM回归模型，存在两个参数C与Gamma。其中C为惩罚系数，表示对误差的容忍度。提高C值，模型误差容忍度降低，训练集回归结果与实际值越接近，但存在过拟合风险。反之减小C值，模型易出现欠拟合。Gamma是选择高斯(RBF)函数作为核函数时，高斯函数自带参数。其决定映射到新的特征空间后分布，Gamma值增大，支持向量数目越少，致使训练集预测结果准确率提升，但对样本的泛化能力减小，易造成过拟合。反之减小Gamma值，模型易出现欠拟合。

经过调整参数，选取C=24，gamma=170作为y方向轴瓦振动LS-SVM回归模型参数，测试集回归值与实际值对比如图5所示，测试集样本预测回归值均方根误差RMSE为0.047 mm。

图5 LS-SVM模型y方向轴瓦振动测试集回归值

3.1.2 自由端轴承温度回归结果

在调整参数后，选用(epochs)=2 000，(batch_size)=12，隐含层神经元为8的LSTM进行回归训练，测试集回归值与训练值对比如图6所示。

图6 LSTM测试集自由端轴承温度预测回归值与实际值对比

图6为测试集数据自由端轴承温度预测回归值与原始值对比，图像中两种状态预测回归值与实际值变化趋势相同，个别样本点差别较大，最大误差为0.23 ℃。测试集样本预测回归值均方根误差RMSE为0.068 1 ℃，较y方向轴瓦振动预测回归值均方根误差有明显增大。

经过调整参数，选取C=0.7，gamma=100作为自由端轴承温度LS-SVM回归模型参数，测试集回归值与实际值对比如图7所示，测试集样本预测回归值均方根误差RMSE为0.125 ℃。

图7 LS-SVM测试集自由端轴承温度预测回归值与实际值对比

y方向轴瓦振动、自由端轴承温度两种模型平均误差RMSE对比如图8所示。

由图8可看出LSTM的两参数回归值的RMSE均小于LS-SVM，且LS-SVM两参数回归值的RMSE近乎为LSTM模型的2倍，故认为LSTM较LS-SVM更适宜于一次风机参数的回归预测。

图8 LS-SVM与LSTM两种模型两参数在测试集上均方根误差对比

3.2 x方向轴瓦振动测点异常故障诊断

基于上述两种回归模型对比结果，仅采用LSTM对x方向轴瓦振动参数进行回归，测试集回归结果如图9所示。

图9中，正常状态区间回归参数与原始参数较变化趋势一致且误差很小，异常状态区间内，回归参数与原始参数发生明显偏离。为进一步验证LSTM模型对故障判别诊断，引入前文所述自适应阈值计算三类参数LSTM回归值自适应阈值区间。考虑正常状态三类参数回归参数与原始参数最大误差，自适应阈值Z的取值如表2所示。

图9 x方向轴瓦振动回归值与原始值正常状态及异常状态曲线

表2 正常状态三类参数自适应阈值参数选取

三类参数的自适应阈值区间与实际参数如图10所示。

由图10(c)可发现发生x方向轴瓦振动测点异常时，原始参数已超过阈值上下限，可认定x方向轴瓦振动存在异常；x方向轴瓦振动异常可能出现风机转子质量不平衡、振动大造成碰撞磨损、支撑刚度下降、轴承损坏等故障，如若发生上述故障，则不仅体现在x方向轴瓦振动值异常，还会体现在y方向轴瓦振动、自由端轴承温度异常；对比图(a)、(b)中正常状态与异常状态，可发现异常状态与正常状态两类参数均处于阈值上下限内，故认为两类参数不存在异常，仅x方向轴瓦振动出现异常，故排除上述故障，仅是x方向轴瓦振动单个测点出现异常，与实际情况相符。