仿古建筑双枋-柱组合件耗能能力研究

2022-10-08董金爽公衍茹薛建阳

海南大学学报（自然科学版） 2022年3期

董金爽，公衍茹，薛建阳，翟磊，黄斌

（1. 海南大学土木建筑工程学院，海南海口，570228；2. 西安建筑科技大学土木工程学院，陕西西安 710055）

仿古建筑作为中国传统建筑文化与现代建筑材料相结合的一种新型建筑形式，因其对传统建筑风格与地域建筑特色具有的良好表现力，是华夏建筑文化在当前社会中的探索与创新［1-2］，如图1a 所示. 当前大型仿古建筑多为殿堂式，其外围檐柱常为双枋-柱形式［3］，即同时存在阑额及由额，如图1b 示.

图1 -柱组合件

因形制特点，仿古建筑中柱构件多为变截面，上柱截面尺寸小于下柱，如图2 示. 节点作为结构传力枢纽，在轴力、剪力、弯矩甚至扭矩的共同作用下处于多轴复杂应力状态. 历次震害表明，仿古建筑节点是结构抗震设计的薄弱环节. 如图3所示，9·21南投地震中武昌宫梁柱节点发生压溃破坏；谢启芳等［4］进行的双枋-柱节点试验表明：仿古建筑双枋-柱节点部位抗震性能难以满足现行规范的相关要求. 目前，对仿古建筑力学性能的研究尚未完全展开. 薛建阳等［5-8］、吴占景等［9］、陶倍林等［10］、张兰香等［11］、李卫俊等［12］均开展了仿古建筑相关的试验、理论及施工工艺研究，取得了一定研究成果.

图2 双枋组合件域示意图

图3 武昌宫震害图

因此，设计3个仿古建筑双枋-柱组合件试件，上柱采用方钢管-混凝土组合结构，并在由额处附设黏滞阻尼器，施加快速往复正弦波荷载，对其滞回特性及耗能能力进行研究.

1 试验概况

1.1 试件设计设计3个仿古建双枋-柱组合件试件，其缩尺比依据《营造法式》中古木结构材份制规定，并结合舟山佛学院实际工程所确定为1∶2.6. 其中2个为附设黏滞阻尼器的仿古建筑组合件试件，编号分别为ZD-2和ZD-3，未附设阻尼器的试件作为对比试件，编号为ZD-1. 各试件构造形式及配筋如图4所示.试件设计轴压比为0.25，商品混凝土强度等级为C40，配合比如表1 示，测得与浇筑试件时同批次混凝土立方体抗压强度标准值fcu，k=45.6 MPa. 方钢管截面尺寸为160 mm×160 mm，采用Q235B，厚度为5.5 mm.各试件中阑额及由额为钢筋混凝土结构，上柱为方钢管混凝土结构，下柱为钢筋混凝土结构，上柱方钢管伸入下柱的长度及方钢管上栓钉锚固要求根据规范及数值模拟分析确定，试件配筋构造如表2 示. 钢材力学性能如表3示.

表1 混凝土配合比单位：kg·m-3

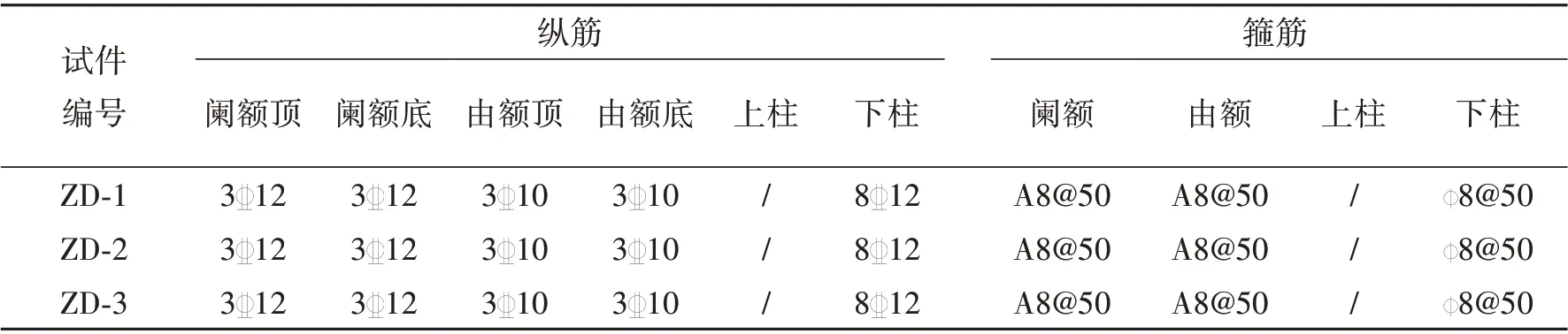
表2 试件设计参数

表3 钢材材性指标

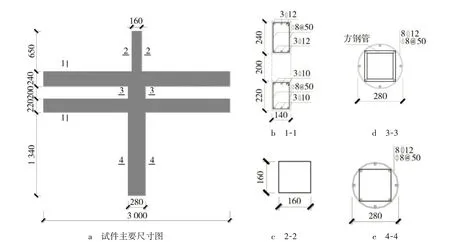
图4 试件详细尺寸及具体构造示意图

1.2 黏滞阻尼器选型及安装选用的黏滞阻尼器设计参数如表4 所示. 黏滞阻尼器与试件连接基本设计尺寸参数如表5及图5. 其中试件ZD-2安装阻尼器CX-1，试件ZD-3安装阻尼器CX-2.

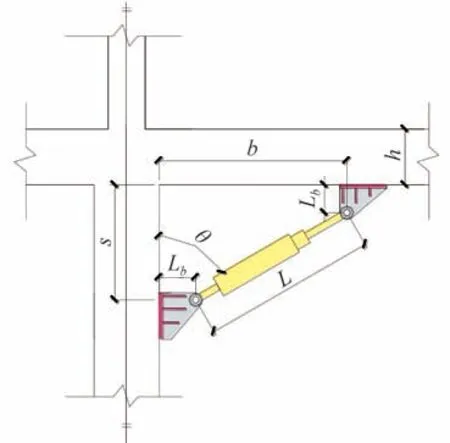
图5 阻尼器连接设计尺寸

表4 试验用黏滞阻尼器基本参数指标

表5 黏滞阻尼器与试件连接基本设计尺寸参数

1.3 加载制度试验时采用如图6加载装置. 加载时，各组合件由额两端与地面通过高强螺栓及定向铰支座相连，上下之间安置双枋连接器（专利号：ZL 201620201513.3）. 其工作原理：通过在上额枋与下额枋之间设置上下2个对称的连接件，连接件中间通过设置滚轴，同时在滚轴所能达到的最远边缘处左右位置各设置一个限位角钢，确保上额枋与下额枋之间不产生弯矩和剪力，只是传递竖向力，且上下梁之间保持一定的竖向距离，如图7示. 试件底部采用球铰装置以保持试件沿加载方向自由转动.

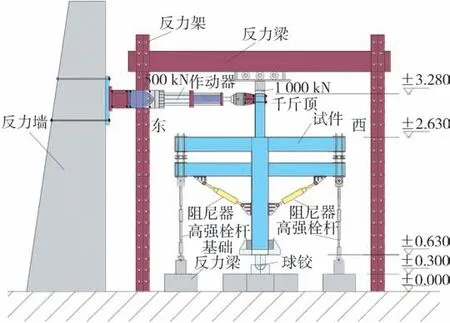
图6 阻尼器连接设计尺寸

图7 双梁连接器示意图

试验加载流程：1）轴压荷载由柱顶油压千斤顶施加；2）水平往复荷载由MTS 电液伺服系统施加. 试验加载工况如表6所示. 荷载形式为正弦波，每工况下反复加卸载10次，加载制度如图8示.

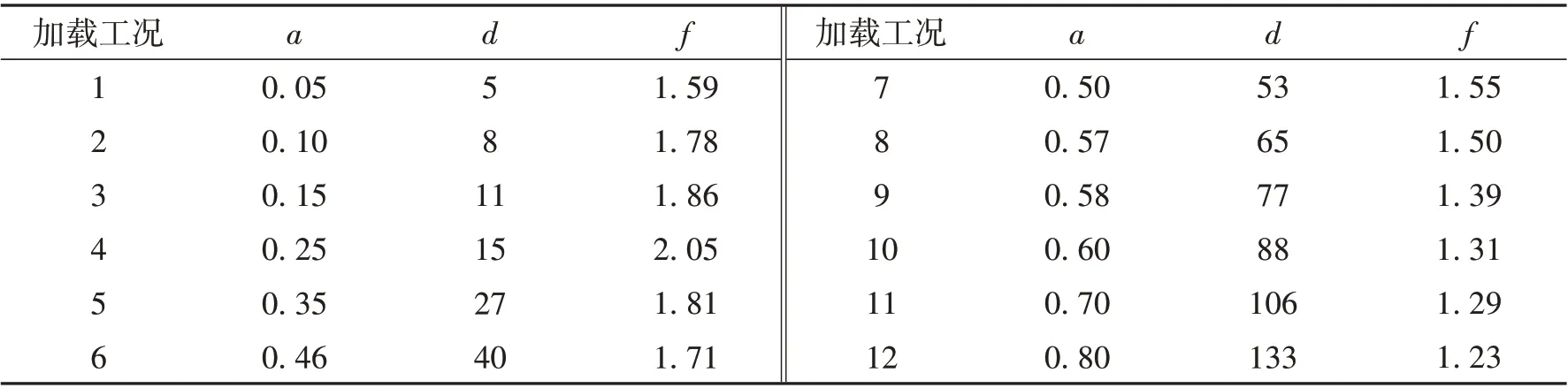
表6 试验加载工况主要加载参数

图8 加载制度示意图

定义试验结束为试件超过峰值荷载后，承载力低于最大承载力的85%，亦或试件轴向荷载不能稳定保持.

1.4 量测方案试验量测内容主要包括：1）节点域混凝土开裂及裂缝发展等破坏情况；2）节点域所布置箍筋应变发展；3）试件恢复力曲线. 试件节点核心域数据采集点如图9所示. 应变片1～2分别粘贴于上下核心域箍筋上，3～8粘贴于纵筋上.

图9 双枋-柱节点核心域应变片布置示意图

2 试验结果及其分析

2.1 试验加载过程对各试件加载全过程进行分析，可将其划分为4个阶段.

开裂阶段：控制位移较小，各试件位移角（以试件水平位移与试件总高的比值）较低，荷载-位移曲线基本呈线性. 加载至工况2时（控制位移8 mm），位移角为1/335，上额枋底部接近枋-柱连接处位置有竖向裂缝. 定义试件出现第一条可见裂缝时的荷载为开裂荷载，分析试验数据可知，未设置阻尼器组合件开裂荷载约为16.6 kN，设置阻尼器组合件开裂荷载，ZD-2、ZD-3 分别为17.8 kN 和18.2 kN，表明设置阻尼器对双枋-柱试件开裂性能影响较小.

屈服阶段：该阶段是指试件开裂后至试件荷载-位移滞回曲线出现明显拐点的受力过程. 随水平位移不断增大，裂缝数量逐渐增多，宽度逐渐增大. 总体上，附设阻尼器的仿古建筑双枋-柱组合件荷载-位移曲线出现明显拐点迟于对比试件，且拐点时的荷载明显高于对比试件.

极限阶段：该阶段是指试件屈服后直至试件水平峰值荷载点的受力过程. 随水平位移不断增大，各试件均出现不同程度的混凝土剥落，裂缝延伸增宽等现象. 各组合件滞回曲线滞回环呈饱满状态，但同控制位移下随着循环次数的增加，峰值荷载逐渐降低，且荷载与位移非线性特性更为显著，表明试件已有显著的刚度退化和承载力衰减. 试件混凝土剥落如图10c和d所示.

图10 试件破坏过程

破坏阶段：各试件在超过最大承载力后，均有不同程度的承载力降低，且存在较大的塑性变形. 对比发现，附设阻尼器试件的试件下降段较平缓，说明试件破坏后试件仍具有一定的耗能能力.

2.2 滞回曲线及骨架曲线整理试验数据得到各试件荷载-位移滞回曲线，并对滞回曲线进行处理得到各试件骨架曲线，如图11所示.

由图11可知：

1）小控制位移时，各试件加卸载曲线基本重合，荷载与位移满足正比例关系；控制位移逐渐增大后，加卸载曲线逐渐分离，包络曲线的面积逐渐增大，试件荷载逐渐提升，但卸载后残余变形也逐渐加大，试件因耗能而产生弹塑性变形.

2）与对比试件相比，附设阻尼器后试件滞回环更饱满，面积更大，表明附设阻尼器可提升仿古建筑组合件的耗能能力. 控制位移不变时，不同循环加卸载形成的包络曲线面积不同，循环次数增加，形成的包络面积逐渐越小，即试件累积损伤逐渐增加.

3）附设阻尼器试件的滞回曲线为较饱满的梭形，其饱满程度及包络曲线的面积均高于同控制位移下的对比试件，说明设置黏滞阻尼器对仿古建筑双枋-柱组合件的耗能能力及延性具有显著的提升.

4）对比图11d各试件骨架曲线可知，骨架曲线基本呈基于原点对称的S形，整个曲线可大致划分为弹性、弹塑性及塑性3个性质不同的阶段. 是否附设粘滞阻尼器对试件弹性刚度影响较小，而对承载能力有较大影响，这是由于在荷载较小时，阻尼器基本不发挥作用；随着位移的增大，阻尼器开始发挥作用，骨架曲线呈现不同的特点，且超过峰值点后，设置阻尼器试件的下降曲线较对比试件更为平缓，无荷载陡降.

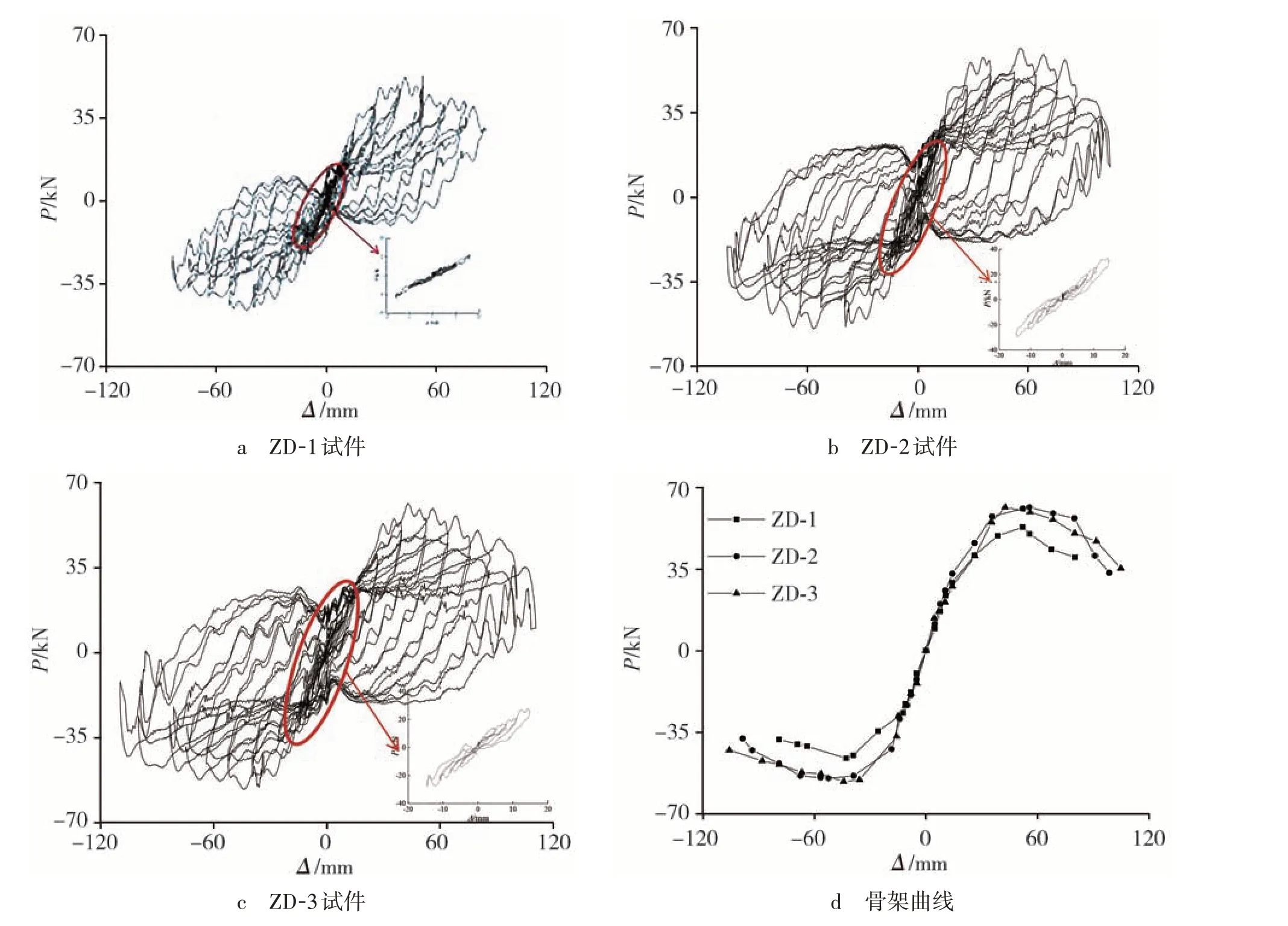
图11 试件荷载-位移滞回曲线及骨架曲线

3 耗能能力分析

《建筑抗震设计规：GB 50011-2010》规定：建筑的基本抗震设防目标是“小震不坏、中震可修、大震不倒”，为确保该目标的实现，结构（构件）必须具有足够的延性与耗能能力.

3.1 非弹性能量吸收因子Fμ及延性分析Fµ为延性比μ的函数，又称延性因子，是指在地震作用下构件进入塑性状态，吸收一定的能量，从而保持其功能的能力. 美国电力研究院（EPRI）［13］计算延性因子时提供了有效频率/有效阻尼法，该方法考虑了力-位移滞回环曲线以及结构进入塑性后导致频率改变的影响因素. 表达式

其中，ρ=q+1，q=3.00δ-0.30，γ=0.48δ-0.08，μ为结构的延性系数；δ为结构的阻尼比，对于钢-混凝土组合结构取δ=0.03.

取位移延性系数为各试件破坏点对应的位移与屈服点的位移的比值，屈服点由能量法确定. 各试件特征点的延性因子及位移延性系数如表7所示. 图12给出了试件特征点荷载及位移变化趋势图. 对结果分析可知：

图12 试件特征点荷载及位移变化趋势图

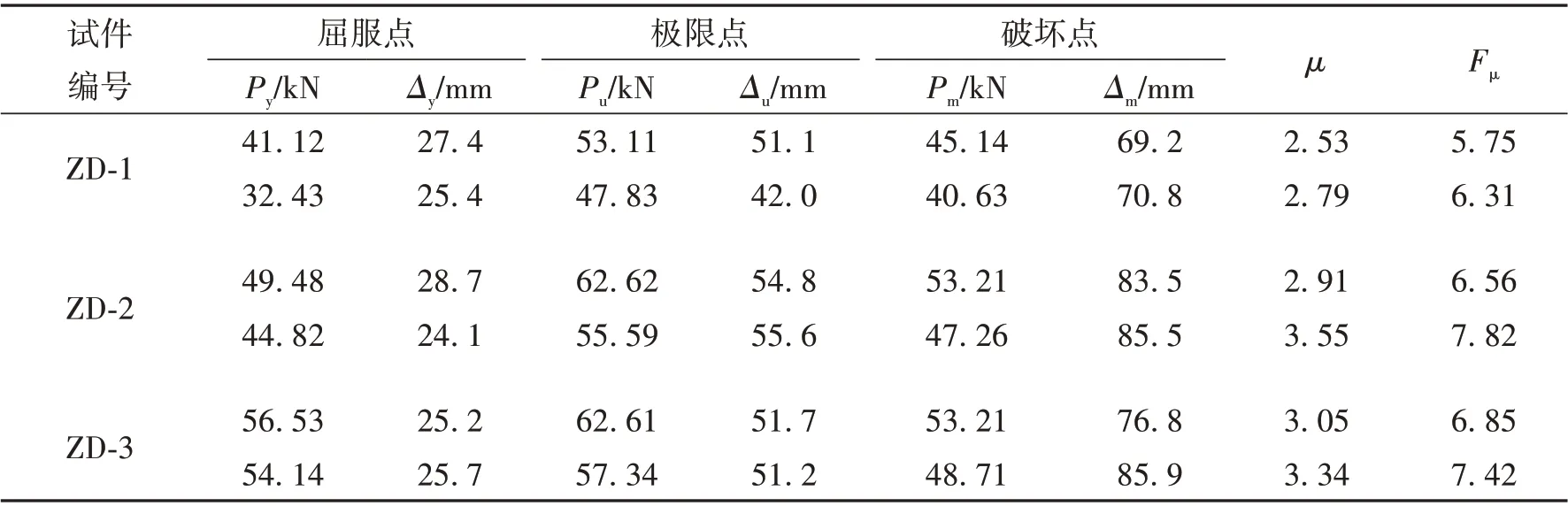
表7 试件特征点、延性系数及延性因子

1）附设黏滞阻尼器后仿古建筑双枋-柱组合件试件的屈服荷载及峰值荷载明显高于对比试件，分别平均提高38.1%、17.2%. 说明附设阻尼器可较大幅度提升试件抵抗外荷载的能力；附设黏滞阻尼器试件的屈服位移及峰值位移与对比试件差别较小，这是由于试验中采用位移控制加载制度，同位移条件下试件的荷载因其参数不同而产生差异.

2）附设阻尼器后，仿古建筑双枋-柱试件的位移延性系数及延性因子相对于对比试件均有不同程度的提升，对于ZD-2，其延性系数及延性因子分别提升21.4%和19.3%；对于ZD-3，其延性系数及延性因子分别提升20.1%和18.3%. 整体上，延性因子提升幅度小于延性提升幅度，说明综合考虑力-位移滞回环曲线以及结构进入塑性后导致频率改变影响因素后，更能体现试件抗震性能变化规律.

3）附设不同黏滞阻尼器设计参数的双枋-柱组合件屈服荷载相差15.6%，而峰值荷载平均值相差仅2.4%，黏滞阻尼器最大设计荷载CX-1 较CX-2 高37.3%，说明黏滞阻尼器最大设计荷载不是影响其对组合件承载能力关键因素. 因此实际工程中要综合考虑多因素，如阻尼系数、阻尼器类型等.

3.2 耗能指标分析结构耗能能力采用等效粘滞阻尼系数he及功比系数IW［14］表征. 计算结果如表8示.分析可知：

表8 试件耗能指标

1）附设黏滞阻尼器后仿古建筑双枋-柱组合件试件的耗能能力明显高于对比试件. 以屈服点及极限点为例，设置黏滞阻尼器试件的he分别平均提高了30.8%和32.1%，而功比系数平均提高了18.0%，说明通过在由额处设置阻尼器是提升仿古建筑耗能能力的一个有效措施.

在参加萨提亚心理治疗模式培训的规培医师中，对8次课程觉得非常好占50%以上，没有人认为不好和差，具体情况详见（表2）。

2）根据现有研究结果，钢筋混凝土结构功比系数分别约为10［15-16］. 通过采用钢-混凝土组合结构形式的仿古建筑组合件的功比系数较钢筋混凝土结构有显著提升，有效地提升了仿古建筑的抗震性能，且设置阻尼器后其功比系数提升幅度更高，表明通过在上柱采用钢-混凝土组合结构及附设黏滞阻尼器可显著提升仿古建筑耗能能力，为其在实际工程中的应用提供了理论基础.

3.3 能量及刚度退化分析采用能量退化及刚度退化对仿古建筑双枋-柱组合件耗能能力进行表征.定义能量退化系数为同级控制位移下不同循环时包络曲线面积的比值，刚度退化采用不同控制位移下第一次循环时形成的滞回曲线最大荷载及其对应的位移的比值，取正负向计算结果的平均值.

各试件在不同加载位移条件下的能量曲线ηi-Δ/Δy及刚度退化曲线Ki-Δ/Δy如图13所示.

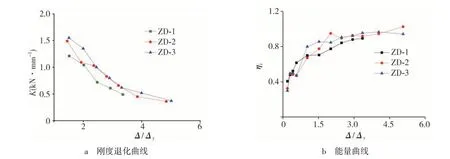
图13 各试件刚度退化及能量曲线

分析图13可知：

1）各试件刚度退化整体上呈先快后慢，这是由于开始加载后试件逐渐出现一系列的裂缝，试件刚度及强度逐渐退化，变化较为明显；加载后期，试件弹塑性及塑性变形较大，损伤累积严重，刚度退化不明显；附设阻尼器组合件刚度退化加载后期更平缓，说明附设阻尼器能提高试件的割线刚度，使试件表现出良好抗震性能.

2）各试件能量退化曲线整体上呈增大趋势，先快后慢，最后趋于平稳. 各试件能量退化曲线基本平行，说明退化趋势基本一致. 能量退化曲线之所以呈逐渐增大，这是由于开始加载时试件变形主要为弹性可恢复变形，耗能能力较低，包络曲线形成的面积较小；随着控制位移的不断增大，包络曲线形成的面积逐渐增加，试件变形主要为不可恢复的弹塑性变形及塑性变形，耗能能力显著提升，试件性能得以充分发挥，滞回曲线包围面积逐渐增大，达到最大面积后开始减小，而此时试件基本达到其极限状态.

3.4 耗能系数耗能系数可用能效指数ξ、单位能效系数表示. 能效指数是指试件屈服后能量耗能能力Ey与结构的能量耗能能力Et比值. 其中ΣEi为试件屈服后第i次加载循环之前结构累积耗散的能量，可取滞回环包围的面积，Et为结构破坏时对应的功比系数与5倍的结构弹性应变能的乘积，即Et=2.5IwPyΔy.

单位能效系数包括单位位移能效系数（λΔ=Et/Δm）、单位荷载能效系数（λP=Et/Pm），其中Δm，Pm分别为试件峰值位移、峰值荷载. 各试件耗能系数如表9所示.

表9 各试件耗能系数

分别定义对比试件的λΔ，λP值为基准值，附设阻尼器组合件试件的λΔ，λP与对比试件对应值的比值作为纵轴，如图14所示.

由图14 可知，附设黏滞阻尼器后仿古建筑双枋-柱组合件耗能系数均高于对比试件. 相对于对比试件，附设黏滞阻尼器后仿古建筑双枋-柱组合件试件的能效指数分别提升了15.5%和26.8%；单位位移能效系数分别提升了42.0%和36.1%；单位荷载能效系数37.5%和39.3%，说明附设阻尼器可较大幅度提升试件的耗能能力. 究其原因是附设的阻尼器在一定程度上消耗外荷载作用在结构或构件上的能量，直观上表现为试件承载能力提升，延性增加.